TEORICO Nº 1_CPR 5º Economia 2014

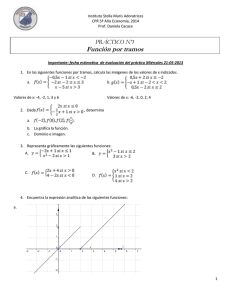
Instituto Stella Maris Adoratrices
CPR 5º Año, 2014
Prof. Daniela Cacace
TEÓRICO Nº 1
Función por tramos
Definición: las funciones por tramos o definidas a trozos son aquellas cuya fórmula consta de dos o más expresiones.
La fórmula varía dependiendo del intervalo del eje x que se considere.
Ejemplo 1:
Sea
Su gráfica estará formada por dos tramos:
El tramo y=5-2x correspondiente al intervalo
El tramo y=3x correspondiente al intervalo
.
Ejemplo 2:
Sea
Su gráfica estará formada por dos trozos.
_____________________________________________________________________________________________
Expresión analítica:
Ejemplo: encuentra la expresión analítica de la función
a partir de la gráfica.
Para x<4, la gráfica es la recta con ordenada al origen
3 y pendiente -2. Luego para x<4, f(x)=-2x+3.
Para x 4, la gráfica es la recta horizontal y=3.
Finalmente:
1
Instituto Stella Maris Adoratrices
CPR 5º Año, 2014
Prof. Daniela Cacace
Función valor absoluto:
La función valor absoluto hace corresponder a cada número real
su valor absoluto.
El valor absoluto de x se representa por .
Dada la función f(x), podemos construir una nueva función de la
siguiente forma:
Para trabajar con este tipo de funciones, resolveremos antes la
inecuación f(x)=0
Ejemplo: sea la función
_______________________________________________________________________________________________
Función parte entera:
Es una función que a cada número real hace corresponder el número entero inmediatamente inferior.
x
0
0,5
0,9
1
1,2
1,5
1,8
2
2,3
f(x)=[x]
0
0
0
1
1
1
1
2
2
Notación: [x] o E(x)
2
Instituto Stella Maris Adoratrices
CPR 5º Año, 2014
Prof. Daniela Cacace
Para recordar:
 Se llama dominio de f al conjunto de valores que toma la variable independiente, x. Se indica como Dom f.
El dominio está formado, por lo tanto, por los valores de x para los que existe la función, es decir, para los
que hay un f(x).
 La imagen de una función es el conjunto de valores que puede tomar la variable dependiente, y, esto es el
conjunto de las imágenes. Se representa como Im f.
 Conjunto de ceros: es el conjunto de puntos pertenecientes al dominio de la función para los cuales dicha
función vale cero.

Conjunto de negatividad: es el conjunto de puntos pertenecientes al dominio de la función para los cuales
dicha función toma valores negativos.
 Conjunto de positividad: es el conjunto de puntos pertenecientes al dominio de la función para los cuales dicha función toma valores
positivos.
Crecimiento y decrecimiento:
Cuando al aumentar el valor de x aumenta el valor de y=f(x), la gráfica "asciende" y se dice que la función es
creciente. Si por el contrario al aumentar x disminuye y, la gráfica "desciende", y la función decrece.
Precisando un poco más:
Una función es creciente en un intervalo, cuando dados dos puntos cualesquiera del mismo
• Si x1<x2 entonces f(x1)<f(x2)
Y será decreciente:
• Si x1<x2 entonces f(x1)>f(x2)
Continuidad:
La primera idea de función continua es la que puede ser representada de un solo trazo, sin levantar el lápiz del
papel. Cuando una función no es continua en un punto se dice que presenta una discontinuidad.
La siguiente función es discontinua en x=2.
.
3
Instituto Stella Maris Adoratrices
CPR 5º Año, 2014
Prof. Daniela Cacace
Funciones especiales:
 Función escalonada: es una función definida en el conjunto de los números reales. E(x) = entero
inmediatamente menor o igual que x. Su gráfica es:
 Función peine inclinado: Estudia ahora la función g (x) definida a partir de la anterior, E(x), y también
definida en el conjunto de los números reales: g(x) = x – E(x).Su gráfica es:
 Función sierra: Es otra función definida en el conjunto de los números reales: s(x) = distancia (positiva) entre
x y el entero más próximo. Ésta es su gráfica.
4