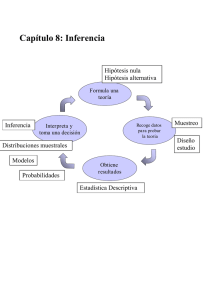
8.2 Inferencia medias

William S. Gosset
Born: 13 June 1876 in Canterbury, England
Died: 16 Oct 1937 in Beaconsfield, England
http://www-groups.dcs.st-and.ac.uk/~history/Mathematicians/Gosset.html
Leer Cuadro 9-1, página 276 de Aron, A. Aron, E.
(2001) Estadística para Psicología. Segunda
Edición. Prentice Hall.
1
8.2 Tomando decisiones acerca de la media
de una población
Hipótesis
Escriba las hipótesis nula y alternativa que
usaría para probar las siguientes aseveraciones.
Las hipótesis deben ser expresadas en términos
de  , la media de la población de interés.
a) La media de la edad de los pacientes en un
hospital es de más de 60 años.
b) La media del contenido de cafeína de una
taza regular de café es de menos de 110 mg.
c) El número promedio de pacientes que
ingresan a la Posta Central diariamente
difiere de 20.
2
Distribución muestral de X , la media
muestral
Si tomamos una muestra aleatoria simple de
tamaño n de una población con media  y
desviación estándar  , y ...
...si la población original distribuye normal,
X 
  
Z=
~ N 0,1
X ~ N  ,



n


n
...si la población original no es
necesariamente normal, pero el tamaño
muestral es suficientemente grande,
X ~ ???,n  30 (TCL) 
Z=
X 

es aprox.N 0,1
n
3
Test Z para la media de una población
 Queremos docimar una hipótesis acerca de la media poblacional
nula es H 0 :   0 , donde
 0 es un valor hipotético de  .
 . La hipótesis
 Asumimos que los datos provienen de una muestra aleatoria de tamaño n, de una
población con distribución Normal con desviación estándar conocida  . El
supuesto de normalidad no es crucial si el tamaño de la muestra es grande.

 Nuestra decisión acerca de
estandarizada x , la cual es:
estará basada en el valor de la media muestral
Z
x  0

n
 Este “score” o puntaje z es el test estadístico, y su distribución bajo H 0 es
aproximadamente N ( 0,1) . Notar que el test estadístico es el mismo, y no depende de
la hipótesis alternativa
 Calculamos el valor-p del test, el cuál depende de la hipótesis alternativa:
Test Unilateral, cola superior
Si
H1 :   0 , entonces el
valor-p es el área a la derecha
del test estadístico observado
bajo H 0 .
Test Unilateral, cola inferior
Si
H1 :   0 , entonces el
valor-p es el área a la izquierda
del test estadístico observado
bajo H 0 .
Test Bilateral
Si
H1 :   0 , entonces el
valor-p es el área afuera de las
dos colas del test estadístico
observado bajo H 0 .
N(0,1)
N(0,1)
p-value
Z OBS
Z
N(0,1)
p-value
2
p-value
Z
Z OBS
p-value
2
-ZOBS
+ZOBS
Z
 Decisión: Si el valor-p es menor o igual al nivel de significación se
rechaza H 0 .
4
¿Monóxido de carbono?
Sea  = media de monóxido de carbono en los
paquetes de cigarrillos. En el pasado esa media ha sido
15 mg, con una desviación estándar de 4,8 mg y
queremos saber si la media actual  es menor que la
media antigua de 15 mg.
Alpine
BensonHedges
BullDurham
CamelLights
Carlton
Chesterfield
GoldenLights
Kent
Kool
LandM
LarkLights
Marlboro
Merit
MultiFilter
NewportLights
Now
OldGold
PallMallLights
Raleigh
SalemUltra
Tareyton
True
ViceroyRichLights
VirginiaSlim
WinstonLights
*Fuente de datos: Federal Trade
http://www.ftc.gov/bcp/menu-tobac.htm
40%
30%
Porcentaje
MARCA
Monóxido de
Carbono
(mg)
13.6
16.6
23.5
10.2
5.4
15.0
9.0
12.3
16.3
15.4
13.0
14.4
10.0
10.2
9.5
1.5
18.5
12.6
17.5
4.9
15.9
8.5
10.6
13.9
14.9
20%
10%
0
5
10
15
20
25
Contenido de Monóxido de Carbono (mg)
Estadísticos descriptivos
N
Contenido de Monóxido
de Carbono (mg)
N válido (según lista)
Media
25
12.528
Desv. típ.
4.7397
25
Commission
5
2

Varianza de la población ( ) desconocida
El cálculo del error estándar de la media muestral
incluye a , pero casi nunca vamos a conocer la
variabilidad en la población en estudio. Cuando se
desconoce el  del universo, el error estándar del
promedio debe calcularse a partir de la desviación
estándar de la muestra:
s 
x
s
n
En este caso ya no es lícito trabajar con la
distribución normal y la variable normal estándar,
z=
x

x
x

 n
1
sino que se trabajará con la variable t de
Student:
x x
t

s
s n
x
Esta variable t sigue una distribución t de
Student con (n-1) grados de libertad.
Ejemplo: Si en la sala hay 24 sillas para 24
estudiantes, ¿cuantas sillas puede elegir el
primer estudiante que entra en la sala? ¿el
siguiente? .... ¿el penúltimo? ¿el último?
2
Propiedades de la distribución t de Student
N(0,1)
t(15)
t(3)
 Los valores de t dependen del número de grados de
libertad, los que se determinan a partir del número
usado en el denominador para el cálculo de la
desviación estándar (s) es decir (n-1).
 La función de densidad de la distribución t de Student
tiene forma de campana simétrica, similar a la
distribución normal N(0,1).
 Es un poco más “chata” y tiene “colas más pesadas”
que la N(0,1).
 Cuando el tamaño de la muestra aumenta, la
distribución t de Student se aproxima a la N(0,1).
3
Uso de la Tabla t:
a) Encuentre el percentil 99 de la distribución t
con 4 gl: t.99(4)
b) Encuentre el percentil 10 de la distribución t
con 30 gl: t.10(30)
c) Encuentre el percentil 95 de la distribución t
con  gl
Se observa, por ejemplo, que el percentil 97,5
que en la curva normal corresponde a un valor
de z = 1,96, en la distribución de t para 24
grados de libertad corresponde a un t de 2,064.
Para n infinito la distribución t de Student es
igual a la normal, pero en la práctica cuando el
número de observaciones es superior a 30, los
valores de z y t ya son tan parecidos que se
puede utilizar como aproximación, la
distribución normal.
4
t(df)
Area 
0
t
Tabla: Percentiles de la distribución t de Student
gl
t 0.60
t 0.70
t 0.80
t 0.90
t 0.95
t 0.975
t 0.99
t 0.995
1
2
3
4
5
0.325
0.289
0.277
0.271
0.267
0.727
0.617
0.584
0.569
0.559
1.376
1.061
0.978
0.941
0.920
3.078
1.885
1.638
1.533
1.476
6.314
2.920
2.353
2.132
2.015
12.706
4.303
3.182
2.776
2.571
31.821
6.965
4.541
3.747
3.365
63.657
9.925
5.841
4.604
4.032
6
7
8
9
10
0.265
0.263
0.262
0.261
0.260
0.553
0.549
0.546
0.543
0.542
0.906
0.896
0.889
0.883
0.879
1.440
1.415
1.397
1.383
1.372
1.943
1.895
1.860
1.833
1.812
2.447
2.365
2.306
2.262
2.228
3.143
2.998
2.896
2.821
2.764
3.657
3.925
3.841
3.604
3.169
11
12
13
14
15
0.260
0.259
0.259
0.258
0.258
0.540
0.539
0.538
0.537
0.536
0.876
0.873
0.870
0.868
0.866
1.363
1.356
1.350
1.345
1.341
1.796
1.782
1.771
1.761
1.753
2.201
2.179
2.160
2.145
2.131
2.718
2.681
2.650
2.624
2.602
3.106
3.055
3.012
2.977
2.947
16
17
18
19
20
0.258
0.257
0.257
0.257
0.257
0.535
0.534
0.534
0.533
0.533
0.865
0.863
0.862
0.861
0.860
1.337
1.333
1.330
1.328
1.325
1.746
1.740
1.734
1.729
1.725
2.120
2.110
2.101
2.093
2.086
2.583
2.567
2.552
2.539
2.528
2.921
2.898
2.878
2.861
2.845
21
22
23
24
25
0.257
0.256
0.256
0.256
0.256
0.532
0.532
0.532
0.531
0.531
0.859
0.858
0.858
0.857
0.856
1.323
1.321
1.319
1.318
1.316
1.721
1.717
1.714
1.711
1.708
2.080
2.074
2.069
2.064
2.060
2.518
2.508
2.500
2.492
2.485
2.831
2.819
2.807
2.797
2.787
26
27
28
29
30
0.256
0.256
0.256
0.256
0.256
0.531
0.531
0.530
0.530
0.530
0.856
0.855
0.855
0.854
0.854
1.315
1.314
1.313
1.311
1.310
1.706
1.703
1.701
1.699
1.697
2.056
2.052
2.048
2.045
2.042
2.479
2.473
2.467
2.462
2.457
2.779
2.771
2.763
2.756
2.750
40
60
120
0.255
0.254
0.254
0.253
- t 0.40
0.529
0.527
0.526
0.524
- t 0.30
0.851
0.848
0.845
0.842
- t 0.20
1.303
1.296
1.289
1.282
- t 0.10
1.684
1.671
1.658
1.645
- t 0.05
2.021
2.000
1.980
1.960
- t 0.025
2.423
2.390
2.358
2.326
- t 0.01
2.704
2.660
2.617
2.576
- t 0.005

gl
5
Test t simple para la media de una población
 Estamos interesados en docimar la hipótesis acerca de la media
de una población  . La hipótesis nula es H0 :    0 donde  0 es
un valor hipotético para  . La hipótesis alternativa da la
dirección del test.
 Se asume que los datos provienen de una muestra aleatoria de tamaño n
de una población con distribución Normal con desviación estándar
desconocida  . El supuesto de normalidad no es crucial si el tamaño de
la muestra es grande.
 Nuestra decisión acerca de  , será en base al valor de la media muestral
x  0
estandarizada x , el cual es
.
s
n
Este es el test estadístico y su distribución bajo H 0 , es una
distribución t con n-1 grados de libertad.
t
 El valor-p del test, depende de la hipótesis alternativa:
Unilateral, cola superior
Si H1 :    0, entonces el
valor-p es el área a la derecha
del test estadístico observado
bajo H 0
Unilateral, cola inferior
Si H1 :    0, entonces el
valor-p es el área a la izquierda
del test estadístico observado
bajo H 0
t(n-1)
t(n-1)
p-value
TOBS T
Bilateral
Si H1 :    0, entonces el valor-p
es el área en las dos colas,
fuera del test estadístico observado
bajo H 0
t(n-1)
p-value
2
p-value
TOBS
T
p-value
2
-TOBS
+TOBS
T
 Decisión: Si el valor-p es menor que el nivel de
significancia entonces rechazamos H 0 .
6
Tiempos de estudio
Un profesor universitario lee un artículo que
discute sobre el tiempo que dedican los alumnos
para estudiar cada semana. El artículo dice que los
alumnos estudian en promedio 7,06 horas por
semana. El profesor cree que los alumnos estudian
más de 7,06 horas por semana en promedio.
El profesor elige una m.a.s. de 15 estudiantes
de su universidad y encuentra que el promedio
muestral de estudio es x  8,43 horas y la
desviación estándar es s  4,32 . Asuma que el
tiempo de estudio semanal sigue una
distribución normal.
a)
b)
c)
d)
Establezca la hipótesis a docimar
Calcule el test estadístico
Encuentre el valor p del test.
Los resultados, ¿son estadísticamente
significativos al 5%?
e) Escriba su conclusión al profesor.
7
H :   7,06
0
Test: H1 :   7,06
  0,05
Test estadístico:
x   0 8,43  7,06 1,37
t


 1,23
s
4,32 / 15 1,1154
n
Valor p = área a la derecha de 1,23 en la tabla
t con 14 g.l.
0,2 > valor p > 0,1
Por lo tanto el valor p > 0,05 por lo que no
podemos rechazar Ho
Conclusión: Con un nivel de significación del
5%, no tenemos suficiente evidencia para
concluir que los alumnos estudian, en
promedio, más de 7,06 horas por semana.
8
Datos del mar Laengelmavesi, Finlandia
Se tiene una muestra de peces
que fueron
pescados en el mar Laengelmavesi de
Finlandia. Se está investigando el peso de los
peces en kilos. Se quiere docimar la
hipótesis de que el peso es menor que 16
kilos. Informe sus resultados.

= promedio de peso de los “percas” (perch)
en kilos
Test estadístico observado:
x   0 15,839 16
t

 0,883
s
1,3618
.
n
56
-0,883 nos dice que la media muestral esta a
0,883 errores estándar debajo de la media
hipotética de 16.
9
Calculo del valor p:
Usando la Tabla t: Ya que el test t observado
de -0,883 cae entre el percentil 10 y el 20, en la
distribución t con 40 grados de libertad, el
valor p estará entre 0,10 y 0,20.
t(55) t(40)
Area=Va lor p
p
-1,303
-0,883
-0,.851
0
t 0,10 t
o b s t0,20
0,10  valor p  0,20
Usando el computador: t = -0,885 y 55
grados de libertad, se obtiene un valor p de
0,19.
Por lo tanto con un nivel de significancia del
10% no podemos rechazar H 0 . Necesitaríamos
un valor  mayor que 0,19 para rechazar H 0 .
10
Concluímos que el peso promedio de las
“percas” en este mar, no es significativamente
menor que 16 kilos (   0,1).
11
Test t simple para la media de una población
 Estamos interesados en docimar la hipótesis acerca de la media
de una población  . La hipótesis nula es H :    donde  es un
valor hipotético para  . La hipótesis alternativa da la dirección
del test.
0
0
0
 Se asume que los datos provienen de una muestra aleatoria de tamaño n
de una población con distribución Normal con desviación estándar
desconocida  . El supuesto de normalidad no es crucial si el tamaño de la
muestra es grande.
 Nuestra decisión acerca de  , será en base al valor de la media muestral
x  0
t

estandarizada x , el cual es
.
s
n
Este es el test estadístico y su distribución bajo H 0 , es una
distribución t con n-1 grados de libertad.
 El valor-p del test, depende de la hipótesis alternativa:
Unilateral, cola superior
Si H1 :    0, entonces el
valor-p es el área a la derecha
del test estadístico observado
bajo H 0
Unilateral, cola inferior
Si H1 :    0, entonces el
valor-p es el área a la izquierda
del test estadístico observado
bajo H 0
t(n-1)
t(n-1)
p-value
TOBS T
Bilateral
Si H1 :    0, entonces el valor-p
es el área en las dos colas,
fuera del test estadístico observado
bajo H 0
t(n-1)
p-value
2
p-value
TOBS
T
p-value
2
-TOBS
+TOBS
T
 Decisión: Si el valor-p es menor que el nivel de
significancia entonces rechazamos H 0 .
12