plantilla con lynk-1

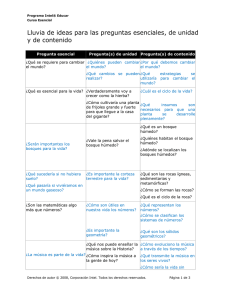
Programa Intel® Educar
Curso Esencial
Plantilla del plan de unidad
Autor de la unidad
Nombre y apellido
FRANCISCO J. BONILLA S.
Nombre de la institución educativa
C.E.B.G. República de Alemania.
Ubicación de la institución educativa
Calle primera, Monte Oscuro. Corregimiento de Victoriano
Lorenzo.
Teléfonos.
517 - 6269 / 517 - 62 70.
Descripción de la unidad
Título de la unidad
De Pangea al mundo actual.
Resumen de la unidad
La necesidad de expresar cantidades donde los números enteros ya no son de utilidad obligó al hombre a crear un
nuevo conjunto. Indagaremos sobre este conjunto, para conocerlo de forma elemental, en situaciones donde podrás
representarlo, definirlo e inclusive medir distancias entre sus elementos y el número cero.
Espacio/s curricular/es o asignatura/s
Aritmética, Geografía, Historia, Español, artística, Música.
Año y nivel
Séptimo grado. Pre Media.
Tiempo necesario aproximado
El proyecto está diseñado para 9 periodos de clase de 35 minutos cada periodo.
Fundamentos de la unidad
Contenidos
Conceptual
 El Conjunto Números
racionales “Q”.
 Recta numérica.
 Valor absoluto.
Procedimental
Identificación de las
características y utilidad de los
números racionales.
Ubicación y representación
de números racionales en la
recta numérica.
Aplicación del valor absoluto
de números racionales.
© 2008 Corporación Intel. Todos los derechos reservados.
Actitudinal
 Predisposición al identificar y
utilizar los números racionales.
 Seguridad al ubicar y representar
en la recta numérica los números
racionales.
 Confianza al aplicar el valor
absoluto de los números racionales.
Página 1 de 5
Programa Intel® Educar
Curso Esencial
Objetivos del aprendizaje
 Escribe, lee, identifica y denota números racionales, valorando su utilidad y aplicándolos correctamente en
situaciones de la vida real, para representar cantidades y resolver problemas.
Indicadores Logros
 Investiga el origen de los números racionales.
 En lluvia de idea discute sobre los diferentes conjuntos numéricos y sus usos.
 Elabora mapa conceptual con los conjuntos numéricos hasta completar los números racionales.
 Debate en el aula sobre las características y utilidad de los números racionales.
 De una lista de números identifica los números racionales.
 Dada la recta numérica con números enteros ubica asertivamente números racionales propuestos en un listado.
 Escribe la distancia que existe entre dos puntos dados en la recta numérica utilizando medidas fraccionarias.
Preguntas orientadoras del plan de unidad
Pregunta esencial
Preguntas de unidad
Preguntas de contenido
¿Por qué los números son importantes?
¿En qué momento empleas los números racionales?
¿Qué son los números racionales?
¿Qué es una fracción?
¿Cuáles son las partes de una fracción?
¿Existen números que se pueden ubicar entre el cero y el uno?
¿Cómo pueden representar los números racionales en una recta
numérica?
¿Qué es el valor absoluto de una fracción?
© 2008 Corporación Intel. Todos los derechos reservados.
Página 2 de 5
Programa Intel® Educar
Curso Esencial
Plan de evaluación
Cronograma de evaluaciones
Antes de empezar el
trabajo del proyecto

Conversatorio sobre el
tema a estudiar.
Durante el desarrollo del proyecto

Rúbrica para
graficar con figuras geométricas.docx
EVALUACIÓN #
1.xlsx

Presentación en cartulina
de lo investigado.
Desarrollo de taller cooperativo acerca
de la representación con figuras
geométricas.

Una vez completado el
proyecto

Evaluación general de los
contenidos tratados.
Evaluación
general.xlsx
Desarrollo de taller cooperativo acerca
de la representación en la recta
numérica.
LISTA DE COTEJO
PARA EVALUAR EL MAPA CONCEPTUAL.docxRúbrica para
graficar con recta numérica..docx
Resumen de evaluaciones
Evaluación
El proyecto se inicia con una lluvia de ideas de los
conceptos previos de los estudiantes de séptimo
grado, se les solicitó que hicieran relaciones con
figuras del entorno que ellos consideraban partibles
o que ya estuvieran fraccionadas.
Dentro de las evaluaciones formativas se orientó de
tal manera que pudiera hacer representaciones con
figuras geométricas y en rectas numéricas.
Por otro lado, en las evaluaciones sumativas, se
desarrollaron talleres y ejercicios de representación
de objetos geométricos para luego partirlos en
pedazos exactos y pintarlos con disposiciones de
colores; también se evaluó exposiciones de los
temas tratados con la ayuda de mapas conceptuales
y otras representaciones
creativas de los
estudiantes.
© 2008 Corporación Intel. Todos los derechos reservados.
Proceso y propósito
El propósito del proyecto es conocer la definición
correcta de fracciones y su relación con el entorno es
por ello que dentro del desarrollo del mismo se
observó un entusiasmo, por parte del estudiantado,
en conocer y proponer diversas situaciones de su
vida cotidiana y buscar la manera de representarla
con fracciones. Fue sumamente interesante que
dentro de sus representaciones hayan utilizado
construcciones de autos, edificios y demás para
luego tratar de partirlos en partes iguales y pintarlos
cuidando de la disposición de colores, se
construyeron diversos mapas donde pudieron
exponer sus impresiones de los contenidos tratados
y sus investigaciones acerca del tema. Por otro lado
se utilizó diapositivas para que los ejemplos en las
representaciones fuesen más reales y coloridos,
ayudando de cierta forma en la maximización de
información y su posterior estudio en casa; por
último se aplicaron pruebas de conocimientos y
representaciones de tal forma que se pudo observar
el avance cognitvo; a través, de mediciones
numéricas.
Página 3 de 5
Programa Intel® Educar
Curso Esencial
Detalles de la unidad
Habilidades previas
Para el desarrollo del proyecto el estudiante debe estar en la capacidad de utilizar el conjunto entero y
sus representaciones, medir y representar utilizando la regla, dibujar y pintar con destreza y
creatividad, conocer las notas musicales y conocer los continentes actuales.
Procedimientos
Los procesos son bases en el desarrollo matemático por lo que para la ejecución del proyecto el
participante debe ser dinámico en la elaboración de estructuras de papel que le ayuden a ejemplificar de
forma real elementos del conjunto racional, un estudiante investigativo que pueda en casa ampliar toda
la información generada en el salón de clases; ya que será evaluado diagnósticamente con los
conversatorios permanentes, formativamente con talleres y construcciones de moldes que les permitan
vivenciar lo aprendido; y sumativamente con pruebas de desarrollo y relaciones con temas de otras
áreas en donde se apliquen los conceptos estudiados y aprendidos en este taller .
Para los estudiantes con NEE, se les adaptara un sistema visual al
representar el conjunto estudiado, las construcciones en la recta
numérica y otros objetos lo harán en casa con sus acudientes de forma
que tenga más tiempo en aprender los contenidos. Mientras que sus
compañeros construyen las representaciones en el salón los estudiantes
con necesidades especiales representarán lo solicitado en moldes
construidos por ellos mismos, de forma previa, en su casa y con el tiempo
necesario para el mismo.
Estudiante con
necesidades especiales
Las definiciones serán construidas por el docente y el estudiante en un
lenguaje sencillo y accesible para el estudiante.
En cuanto a la evaluación el estudiante traerá rectas numéricas dibujadas
desde su casa y pedazos redondeados de cartón de colores para que
pueda colocarlo en el lugar asignado en una prueba de reconocimiento de
posiciones en la recta numérica y no así la construcción y división de
recta numérica en el aula de clases ya que esto le puede tomar mucho
tiempo.
Durante todo el proceso se le guiará con preguntas y conversatorios
donde se le pueda evaluar lo que aprende de forma verbal y hacer las
observaciones en el cuaderno para que sus padres refuercen en casa lo
aprendido en el aula de clases.
© 2008 Corporación Intel. Todos los derechos reservados.
Página 4 de 5
Programa Intel® Educar
Curso Esencial
No hispano-parlantes
Estudiante talentoso
Los estudiantes con esta característica se le asignarán un guía y
traductor para que pueda escuchar la lección en su lengua materna o más
utilizada. Se utilizará mucho la herramienta de internet para trasladar
contenidos de un idioma a otro y al mismo tiempo pueda observar
tutoriales elaborados en su idioma por diferentes autores, con el cuidado
de discriminar la información buscada.
El estudiante talentoso nos servirá de guía y monitor para colaborar en la
atención de compañeros con mayor dificultad y para que la clase sea
dinámica y si es posible dar atención individualizada a cada uno de los
miembros de la clase. Se le asignará temas puntuales de materias
correlacionadas donde se pueda aplicar los números racionales, para que
se los presente a sus compañeros y así enriquecer la aplicación de los
aprendizajes en otras áreas.
Materiales y recursos necesarios para la unidad
Tecnología – Hardware (equipo necesario)
Cámara
Disco láser
VCR
Computadora(s)
Impresora
Cámara de vídeo
Cámara digital
Sistema de proyección
Equipo de vídeo conferencia
Reproductor de DVD
Escáner
Otro
Conexión a Internet
Televisor
Tecnología – Software (necesario)
Base de datos/Hoja de cálculo
Editor de imágenes
Desarrollo de páginas web
Diagramador de publicaciones
Buscador Web
Procesador de texto
Programa de correo electrónico
Multimedia
Otro
Enciclopedia en CD-ROM
Materiales impresos
Suministros
Recursos de Internet
Otros Recursos
Libros de texto, materiales de referencia.
Hojas blancas, cartulinas, metro, lápiz de colores.
Direcciones web (URLs) que apoyan la implementación de su unidad
Visitas de campo, experimentos, oradores invitados, mentores, otros
estudiantes/clases, miembros de la comunidad, padres, etc.
Los programas de Intel® Educación son financiados por la Fundación Intel y la Corporación Intel.
Derechos reservados ©2008, Corporación Intel. Todos los derechos reservados. Intel, el logo de Intel, la iniciativa de Intel Educación y el
Programa Intel Educar son marcas registradas de Intel Corporation o de sus subsidiarias en los Estados Unidos y otros países. *Otros nombres
y marcas pueden ser reclamadas como la propiedad de terceras partes.
http://www.intel.com/content/www/xl/es/education/k12/assessing-projects/assessment-plans/secondary/great-thinkers.html
© 2008 Corporación Intel. Todos los derechos reservados.
Página 5 de 5