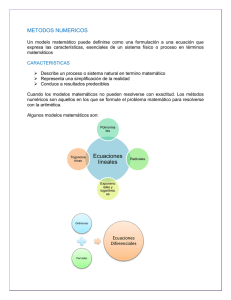
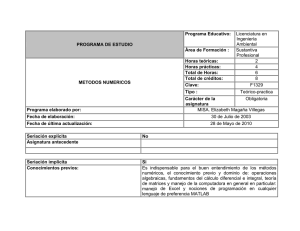
3043 Metodos numericos

GOBIERNO CONSTITUCIONAL DEL ESTADO LIBRE Y SOBERANO DE OAXACA
INSTITUTO ESTATAL DE EDUCACIÓN PÚBLICA DE OAXACA
COORDINACIÓN GENERAL DE PLANEACIÓN EDUCATIVA
COORDINACIÓN GENERAL DE EDUCACIÓN MEDIA SUPERIOR Y SUPERIOR
PROGRAMA DE ESTUDIOS
NOMBRE DE LA ASIGNATURA:
MÉTODOS NUMÉRICOS
CICLO
CUARTO SEMESTRE
CLAVE DE LA ASIGNATURA
3043
TOTAL DE HORAS
102
OBJETIVOS GENERALES DE LA ASIGNATURA:
Que el alumno conozca y comprenda la importancia de los métodos numéricos para analizar y solucionar problemas de
ingeniería, utilizando herramientas computacionales.
1.
TEMAS Y SUBTEMAS
ERRORES Y APROXIMACIONES.
1.1. Concepto de error.
1.2. Errores por truncamiento.
1.3. Errores por redondeo.
1.4. Representación del error absoluto.
1.5. Representación del error relativo.
1.6. Representación del error porcentual.
1.7. Propagación del error en las operaciones elementales.
1.8. Detección y corrección de errores.
2.
ECUACIONES NO LINEALES.
2.1. Método de punto fijo.
2.2. Método de Newton-Raphson.
2.3. Método de la secante.
2.4. Método de bisección.
2.5. Aceleración de convergencia.
3.
SISTEMAS DE ECUACIONES LINEALES.
3.1. Método de eliminación Gaussiana con pivote (pivote parcial, pivote escalonado y pivote completo).
3.2. Factorización LU.
3.3. Factorización Cholesky.
3.4. Método de Jacobi.
3.5. Método de Gauss-Seidel.
4.
SISTEMAS DE ECUACIONES NO LINEALES.
4.1. Método del punto flotante.
4.2. Método de Newton-Raphson.
4.3. Método de Newton-Raphson modificado.
5.
INTERPOLACIÓN.
5.1. Interpolación de Lagrange.
5.2. Diferencias divididas.
5.3. Interpolación de Newton.
5.4. Estimación de errores.
6.
DIFERENCIACIÓN E INTEGRACIÓN NUMÉRICA.
6.1. Fórmulas de diferencias divididas hacia adelante.
6.2. Fórmulas de diferencias divididas finitas hacia atrás.
6.3. Fórmulas de diferencias divididas finitas centradas.
6.4. Fórmulas de Newton-Cotes (abiertas y cerradas).
6.5. Integración numérica compuesta.
7.
APROXIMACIÓN CON MÍNIMOS CUADRADOS.
7.1. Aproximación lineal.
7.2. Aproximación polinomial.
7.3. Linealización de ecuaciones no lineales.
7.4. Aproximación lineal múltiple.
8.
ECUACIONES DIFERENCIALES ORDINARIAS.
8.1. Método de Euler.
8.2. Métodos de Runge-Kutta [Orden 1ro - 4to ].
8.3. Ecuaciones diferenciales de orden superior.
8.4. Sistemas de ecuaciones diferenciales.
ACTIVIDADES DE ENSEÑANZA-APRENDIZAJE:




Discutir y analizar los contenidos en forma ordenada, exhaustiva y promoviendo la participación de
estudiantes.
Utilizar Software matemático (Matlab, Mathcad, Mathematica, Maple, Derive) y/o lenguajes de programación
C++, Fortran), para la implementación de los diferentes métodos estudiados.
Analizar la aplicación de las definiciones del tema en problemas reales relacionados con la ingeniería
computación.
Proporcionar al estudiante una lista de problemas del tema y elaborar prácticas de laboratorio para confirmar
resultados obtenidos.
los
(C,
en
los
CRITERIOS Y PROCEDIMIENTOS DE EVALUACIÓN Y ACREDITACIÓN:
Al inicio del curso el profesor indicará el procedimiento de evaluación para la obtención de la calificación final, de la cual el
50% lo representará el promedio de las calificaciones parciales y el otro 50 % el examen ordinario. Para tener derecho a cada
evaluación, el alumno deberá cumplir con un mínimo de 85% de asistencia.
BIBLIOGRAFÍA (TIPO, TÍTULO, AUTOR, EDITORIAL Y AÑO):
BÁSICA




Métodos numéricos para ingenieros, Chapra, S.C., Canale, R.P, Cuarta edición, Editorial McGraw Hill, 2003.
Elementos de métodos numéricos para ingenieros, Gómez Jiménez R., Editorial McGraw Hill, México, 2002.
Métodos numéricos aplicados a la ingeniería, Nieves H. A., Domínguez S. F., Segunda edición, Editorial
CECSA, 2002.
Métodos Numéricos, Rodolfo Luthe, Antonio Olivera, Editorial Limusa, 1985.
CONSULTA

Chapra, S.C., Canale, R.P. "Métodos numéricos para ingenieros", 5a Ed., McGraw-Hill, 2007.

Gómez Jiménez R., Elementos de Métodos Numéricos para ingenieros, McGraw Hill, México, 2002.

Nieves, H. A., Domínguez S. F., “Métodos numéricos aplicados a la ingeniería“, 2a Ed., CECSA, 2002.

Rodolfo Luthe, Antonio Olivera y Fernando Schutz, Metodos Numericos, Limusa.
PERFIL PROFESIONAL DEL DOCENTE:
Maestría o doctorado en matemáticas o área afín.
Experiencia profesional y docente mínima de 1 año.