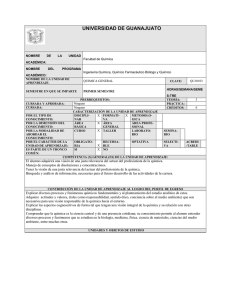
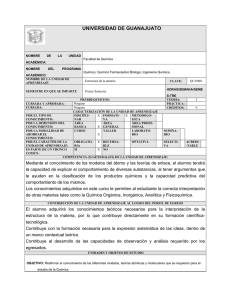
MA10207 Calculo de una variable
Anuncio

UNIVERSIDAD DE GUANAJUATO NOMBRE DE LA UNIDAD Facultad de Química ACADÉMICA: NOMBRE DEL PROGRAMA Químico, Químico Farmacéutico Biólogo e Ingeniero Químico ACADÉMICO: NOMBRE DE LA UNIDAD DE APRENDIZAJE: Cálculo de una variable SEMESTRE EN QUE SE IMPARTE CURSADA Y APROBADA: CURSADA: PRIMER SEMESTRE PRERREQUISITOS: Ninguno Ninguno CARACTERIZACIÓN DE LA UNIDAD DE APRENDIZAJE X METODOLÓDISCIPLIFORMATINAR VA GICA X ÁREA ÁREA ÁREA PROFEBÁSICA GENERAL SIONAL X LABORATOCURSO TALLER RIO CLAVE: MA10207 HORAS/SEMANA/SEME S-TRE TEORÍA: PRÁCTICA: CRÉDITOS: POR EL TIPO DE CONOCIMIENTO: POR LA DIMENSIÓN DEL CONOCIMIENTO: POR LA MODALIDAD DE SEMINAABORDAR EL RIO CONOCIMIENTO: X OPTATIVA POR EL CARÁCTER DE LA OBLIGATORECURSASELECTIX BLE UNIDAD DE APRENDIZAJE: RIA VA X NO ES PARTE DE UN TRONCO SÍ COMÚN: COMPETENCIA (S) GENERAL(ES) DE LA UNIDAD DE APRENDIZAJE: 5 2 12 ACREDI -TABLE Desarrollar las habilidades para resolver problemas. Coadyuvar para lograr el modelaje algebraico. CONTRIBUCIÓN DE LA UNIDAD DE APRENDIZAJE AL LOGRO DEL PERFIL DE EGRESO Aporta al alumno los conocimientos teóricos en el área de la Matemática y el razonamiento algorítmico para la correcta toma de decisiones, promoviendo el trabajo en equipo, estimulando igualmente el espíritu crítico, fomentando el autoaprendizaje, el respeto a su persona, a la sociedad y al entorno; creando una actitud de responsabilidad y liderazgo, considerando en todo momento los valores éticos. UNIDADES Y OBJETOS DE ESTUDIO OBJETIVO: Comprender y aplicar los teoremas y corolarios del Calculo Diferencial e Integral a la solución de problemas. CONTENIDO: 1. Identificar funciones y reconocer las propiedades de límite y continuidad 2. Derivada y aplicar los teoremas de derivación 3. Determinar valores extremos y puntos de inflexión 4. Obtener la integral de diversas formas funcionales 5. Técnicas de integración 6. Formas indeterminadas e integrales impropias 7. 8. Aplicaciones de la integral Introducción al cálculo de varias variables SUGERENCIAS METODOLÓGICAS Considerando que la modalidad de abordar el conocimiento es en forma de “taller”, permite que el estudiante participe de manera activa en el proceso de E-A y que el estudio de la materia sea dinámico e intensivo. Se deben distinguir las actividades ha realizar tanto en las clases de teoría como en laboratorio. Se sugiere que en las actividades de laboratorio, se propongan proyectos sencillos en los que el estudiante aplique los pasos básicos a seguir en la solución de un problema: a) comprender el problema (¿cuál es la incógnita?,¿son suficientes los datos? b) Concebir un plan (Determinar la relación entre los datos y la incógnita) c) Ejecutar el plan d) Discutir la solución obtenida Los proyectos podrán realizarse en equipo (no más de 4 alumnos) 1. a) b) c) SUGERENCIAS PARA LA EVALUACIÓN DE LOS APRENDIZAJE Evaluación 2 exámenes parciales 1 examen final ( puede ser el examen departamental) Proyectos de laboratorio 2. Calificación 20% examen parcial 1 20% examen parcial 2 20% examen final 20% laboratorio 20% asistencia y participación en clase 1. 2. 3. BIBLIOGRAFÍA BÁSICA Stewart, James. Calculus Concepts and Contexts. Brooks Cole Publishing, 1998 Leithold Louis. El Cálculo. Oxford University Press, 1998 Stein, Srerman; Barcillos A. Cálculo y Geometría Analítica. Mc.Graw Hill, 1995 BIBLIOGRAFÍA COMPLEMENTARIA 1. 2. 3. Courant R. John. Introducción al Calculo y al Análisis Matemático. Editorial Limusa. 1979 S.L. Salas, C.G. Salas. Curso de preparación para el Cálculo. Editorial Limusa, 1982 Granville, P. Smith, W. Longley. Cálculo Diferencial e Integral. Editorial Limusa, 1990 ELABORADA POR: Comisión de tronco común y profesores invitados FECHA DE ELABORACIÓN: 0ctubre-2007 FECHA DE REVISIÓN