Documento 257039

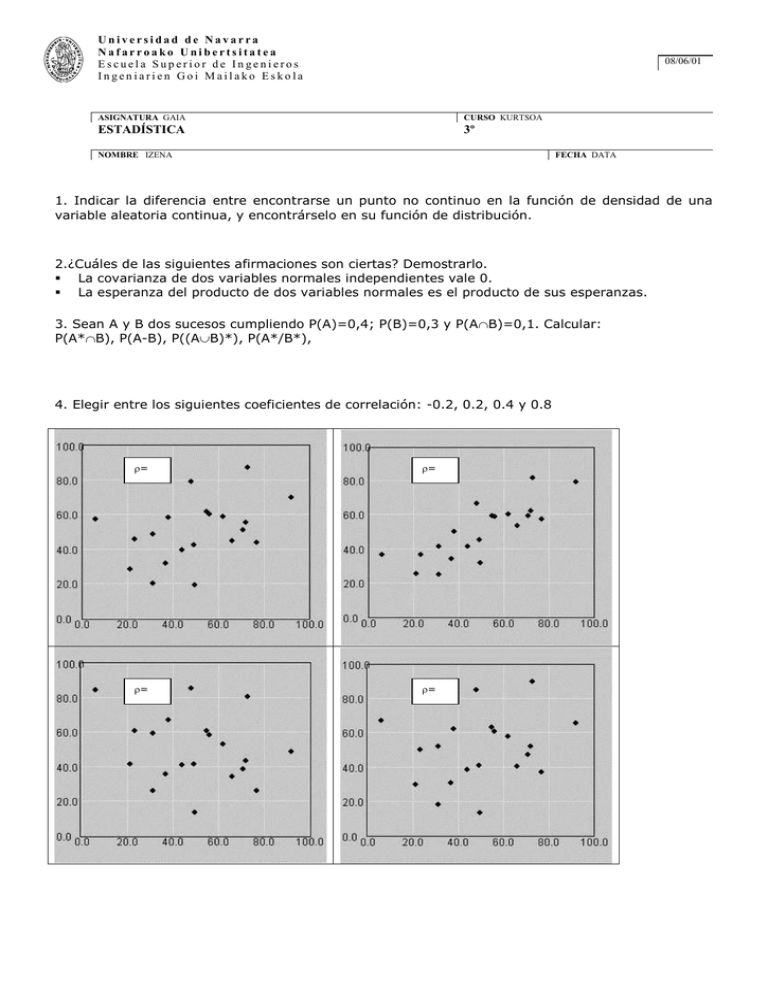
Universidad de Navarra
Nafarroako Unibertsitatea
Escuela Superior de Ingenieros
Ingeniarien Goi Mailako Eskola
08/06/01
ASIGNATURA GAIA
CURSO KURTSOA
ESTADÍSTICA
3º
NOMBRE IZENA
FECHA DATA
1. Indicar la diferencia entre encontrarse un punto no continuo en la función de densidad de una
variable aleatoria continua, y encontrárselo en su función de distribución.
2.¿Cuáles de las siguientes afirmaciones son ciertas? Demostrarlo.
 La covarianza de dos variables normales independientes vale 0.
 La esperanza del producto de dos variables normales es el producto de sus esperanzas.
3. Sean A y B dos sucesos cumpliendo P(A)=0,4; P(B)=0,3 y P(AB)=0,1. Calcular:
P(A*B), P(A-B), P((AB)*), P(A*/B*),
4. Elegir entre los siguientes coeficientes de correlación: -0.2, 0.2, 0.4 y 0.8
=
=
=
=
5. Se lanza una moneda tres veces y se consideran las variables:
X: nº de caras obtenido
Y: diferencia, en valor absoluto, entre el nº de caras y el de cruces.
Calcular la función de distribución conjunta y demostrar si X e Y son variables aleatorias
independientes?
6. Una máquina empaqueta lotes de folios. El dueño de la máquina desea que, al menos, el 90% de
dichos lotes tengan más de 1000 folios no defectuosos. Sabiendo que la probabilidad de que un folio
sea defectuoso es del 2% ¿qué número de folios deberá poner en cada lote?
7. Las calificaciones del primer y segundo parcial de una asignatura se distribuyen normalmente con
media un 4 y desviación típica 1 en el primero, mientras que la media es de 5 y la desviación típica
2 en el segundo, con un coeficiente de correlación de 0,8. Un alumno aprueba la asignatura si la
media aritmética de las dos calificaciones es al menos 5, ¿cuál es entonces la probabilidad de que de
un grupo de 8 amigos, sólo aprueben la asignatura 3?
8. Una tienda de productos de papelería asume que el número de horas semanales que trabajan los
empleados en la tienda es de 36,7 horas, con una desviación típica de 1,5 horas. Su jefe desea
comprobar la certeza de estos valores en base a la observación de las últimas 20 semanas de
trabajo. Así, si el promedio aritmético de las horas de trabajo por cada empleado no difiere del valor
medio real de horas que trabajan en más de 1 hora, con una probabilidad del 90%, seguirá
manteniendo los valores promedios iniciales. ¿Debe entonces cambiar el jefe de opinión en cuanto
cual es el nº medio de horas de trabajo semanal por empleado? ¿Y si hubiese sido tomado la
decisión en base a los datos de las 3 últimas semanas?
9. Para determinar la cuantía que las becas para libros otorgará el Ministerio de Educación el curso
que viene, se desea tener una idea de lo que realmente invierten los alumnos en libros, por
cuatrimestre. Para ello, se han conseguido los datos de 50 alumnos recogidos en la siguiente tabla,
x100 pts. aproximadas al precio “redondo” más próximo:
125
165
148
136
179
205
209
235
265
245
157
191
197
205
217
148
152
113
119
117
145
148
225
119
221
222
165
148
127
148
168
105
108
204
209
178
224
228
115
201
125
158
136
178
104
157
247
187
239
150
Por conveniencia agrupar los datos utilizando intervalos de longitud 25 empezando en 100 y
calcular, en base a los datos agrupados, la media, la mediana y la desviación típica o estándar. Si el
Ministerio ha decidido que la cuantía de la beca será un 10% más del valor de la mediana, ¿qué
porcentaje de estudiantes cubrirán todos sus gastos?
10. En una fábrica la máquina 1 produce piezas de buena calidad en el 80% de los casos, mientras
que esta proporción es del 90% si las piezas proceden de la máquina 2. Se separa una pieza de
cada máquina
a) Cuál es entonces la probabilidad de que ambas piezas sean defectuosas?,
b) Y la probabilidad de que una sea defectuosa y la otra no?
c) Y si se tomaran dos piezas de la producción de un día y se observa que ambas son buenas, ¿cuál
es la probabilidad de que ambas procedan de la máquina 2?
d) ¿Y la de que procedan una de la máquina 1 y la otra de la máquina 2?