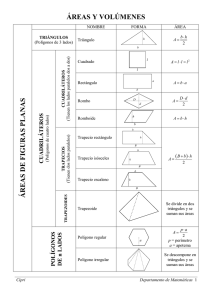
Por una parte, el estudio de las propiedades de las figuras y de los

TALLER DE RESOLUCIÓN DE PROBLEMAS EN GEOMETRÍA
En este taller abordaremos la resolución de problemas desde un modo de pensar
propio del saber geométrico.
¿Cómo entendemos este “modo de pensar”?
Como aquel que nos permite, mediante un razonamiento deductivo, establecer
nuevas relaciones de las figuras y de los cuerpos a partir de las ya conocidas.
Desde esta perspectiva, el estudio de los objetos geométricos no se reduce a
reconocerlos por medio de un dibujo y enunciar propiedades básicas, sino implica
disponer de ellas como herramientas para resolver problemas que requieran más
que una constatación usando representaciones gráficas y/o mediciones efectivas.
En consecuencia, en este taller trabajaremos con problemas geométricos que
cumplan con las siguientes características:
“- Para resolverlo se deben poner en juego las
propiedades de los objetos geométricos.
- El problema pone en interacción al alumno con objetos
que ya no pertenecen al espacio físico, sino a un espacio
conceptualizado; las figuras-dibujo trazadas por este este
sujeto no hacen más que representarlo.
- La función que cumplen los dibujos en la resolución del
problema no es la de permitir arribar a la respuesta por
simple constatación sensorial.
- La validación de la respuesta dada al problema – es
decir la decisión autónoma del alumno acerca de la verdad
o falsedad de la respuesta- no se establece
empíricamente, sino que se apoya en las propiedades de
los objetos geométricos. Las argumentaciones a partir de
las propiedades conocidas de los cuerpos y figuras,
producen nuevo conocimiento sobre los mismos.”1
Pretendemos generar un espacio de trabajo que proponga momentos de
exploración, búsqueda de estrategias, confrontación, discusión y momentos de
acuerdos colectivos acerca de resultados establecidos y procedimientos
desarrollados.
1
Barallobres, G., Fioriti, G., Itzcovich, H. y Sessa, C. (2002), Desarrollo curricular en geometría.
Documento interno. Dirección de Currícula, Secretaría de Educación, G. C. B. A.
¿Cuáles serán los conocimientos básicos que se necesitarán para abordar los
problemas que se propondrán en el taller?
Será necesario recurrir a conocimientos geométricos estudiados en la escuela
secundaria tales como:
 Relaciones entre rectas cortadas por una transversal y los ángulos
determinados por ellas.
 Teorema de Pitágoras.
 Teorema de Thales.
 Clasificación de triángulos y cuadriláteros.
 Nociones de alturas, medianas, mediatrices, bisectrices de un triángulo.
 Criterios de Congruencia y Semejanza de triángulos.
 Cálculo de perímetros y áreas de polígonos y de círculo.
 Nociones de diámetro, arco, cuerda, ángulo inscripto y ángulo central de
una circunferencia.
 Definiciones de funciones trigonométricas. Teorema del seno, teorema
del coseno.
Por último, a modo de ejemplo, invitamos a pensar los siguientes problemas desde
la forma de trabajo propuesta para este taller.
Problema 1:
El siguiente dibujo representa un paralelogramo ABCD:
Si I es el punto medio de AD, J es el punto medio de DC y P es el punto donde se
cortan IJ y DB. ¿Será cierto que P es punto medio de IJ? ¿Por qué?
Problema 2:
Si en un triángulo rectángulo uno de los ángulos agudos mide 30º, ¿Será cierto que
el cateto opuesto a dicho ángulo mide la mitad de la hipotenusa? ¿Por qué?
Problema 3:
ABCD es un trapecio con AB // CD y O es el punto de corte de las diagonales. En
caso de ser posible, establecer la relación hay entre las áreas de los triángulos:
a) ABC y ACD.
b) AOD y BOC.
Lic. Silvia Colombo
Mg. Mabel Licera
Dpto. de Matemática. Facultad de Ciencias Exactas Fco-Qcas. y Naturales. UNRC