Documento 195396

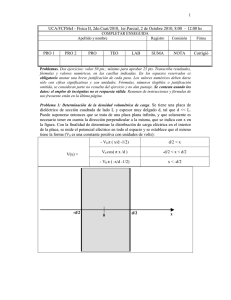
Física II para Licenciaturas de Física y Matemática
Parcial de FISICA GENERAL II – 13 de Octubre 2011
Datos: g = 9,8 m/s2 ; 0 = 8,854×10-12 C2/(N·m2), k= 8,988×109 N·m2/C2
4R 3
3
Esfera: volumen
; superficie 4R
2
1) Dos cargas puntuales se encuentran sobre un eje x según
se muestra en la figura. La carga q1 se encuentra en x = 0 y
la carga q2 en x = d. La gráfica muestra la componente
según el eje x del campo eléctrico producido por dichas
cargas sobre el eje x. Puede concluirse que las cargas:
a) Son del mismo
signo y
b) Son de distinto
q2
4
q1 
signo y
c) Son del mismo
signo y
q1 
q2
4
d) Son de distinto
q2
3
signo y
e) Son de distinto
signo y
q1 
q1 
q2
3
f) Son de igual signo
q1  4q2
q1  4q2
y
Como el campo se anula en un punto entre las dos cargas, necesariamente las mismas deben tener
el mismo signo, pues de lo contrario se sumarían.
Si las cargas tienen el mismo signo, el campo eléctrico entre ambas tiene sus sentidos opuestos, y
como se anula para x  d , para dicho punto los módulos de los campos que crea q 1 y q2 deben ser
3
iguales:
kq1
d 
 
3

2
kq2
 2d 
 
 3 

2
9kq1 9kq2
q

 q1  2 Si q1y q2 son por ejemplo positivas:
2
2
4
d
4d
Se verifica que: para x< 0 E=E1+E2<0
Para: x    E  0

x  0   E  
x  d   E  
x    E  0 
Por tanto a) es la opción correcta.
2)
El campo eléctrico en la atmósfera sobre la superficie terrestre está dirigido hacia abajo y vale
aproximadamente E0= 200 V/m. A una altura h = 1000 m por encima de la superficie terrestre el campo
eléctrico de la atmósfera es de sólo Eh= 40,0 V/m, también dirigido hacia abajo. ¿Cuál es la densidad media
de carga en la atmósfera por debajo de 1000 m de altura, expresada en C/m3?
a)+1,14×10-12 b)-1,14×10-12
Ejercicio del año
c)+1,42×10-12
d)-1,42×10-12
e)+1,14×10-9
f) -1,14×10-9
Consideremos como superficie gaussiana un cilindro circular de sección A, generatrices verticales,
cuya base está sobre la superficie terrestre (h=0) y la “tapa” está en h= 1000 m.

 E  E.nˆ dA 
S
 E.nˆ
base
dA 
Base
 E.nˆ
tapa
dA 
tapa
 E.nˆ
Slateral
dA 
Slateral
De las tres integrales, la que se calcula sobre la superficie lateral es nula, ya que E  nSlateral
E 
 E dA   EdA E (h  0) A  E (h  1000 m) A  E (h  0)  E (h  1000 m)A
Base
tapa
Por la ley de Gauss,  E 
q
0
siendo q la carga encerrada en el cilindro: q  Ah
E(h  0)  E (h  1000m)A  Ah     0
0
= 1,42×10-12 C/m3
E (h  0)  E (h  1000 m) =
 40 =1,41664×10-12 C/m3
8,854  10 12  200
h
1000
Física II para Licenciaturas de Física y Matemática
3) Una esfera de radio
r
a
2
uniformemente cargada, con densidad volumétrica
de carga 1, se sitúa concéntricamente a otra esfera hueca que tiene una
densidad volumétrica de carga 2, de radio interior a y radio exterior 2a, como se
muestra en la figura.
Si el campo eléctrico en
r
3a
2
es nulo. ¿Qué relación
existen entre las densidades de carga volumétricas 1 y 2?
a) 1 =-152
b) 1 =-112
c) 1 =-92
d) 1 =-5,52
e) 1 =-212
f) 1 =-192
El campo eléctrico va a tener simetría esférica, por tanto por la ley de Gauss para una esfera
concéntrica de radio r, se tiene que:
2
 E.nˆ dA   EdA  E(r ) dA  E(r ) 4 r 
S
S
Para r 
S
0
siendo q la carga encerrada.
3a
el campo eléctrico es nulo, por lo que la carga encerrada debe ser cero.
2
4  a 
4
  1 
3 2
3
3
0  q(r ) 
q(r )
  3a  3

    a 3  2
 2 



3
 1
a
19
a3
 27

   2  1  19 2
  2  a 3  a 3   0  1
8
8
8
 8

1 =-192
Física II para Licenciaturas de Física y Matemática
4) Una distribución esférica de carga de radio R1 con carga total
-q se sitúa concéntricamente dentro de un cascarón esférico de
carga de radio R2 =5 R1 con carga total +q. Desde el exterior
de esta distribución de carga se envía un electrón con velocidad
v en dirección radial hacia el centro de la distribución de carga.
¿Cuál debe ser la velocidad mínima vmin para que el electrón,
atravesando el cascarón de carga por un pequeño orificio
practicado en él, llegue a la distribución esférica central?
a)
2eq
5 0 me r
b)
3eq
5 0 me r
c)
eq
5 0 me r
d)
eq
4 0 me r
e)
eq
2 0 me r
f)
eq
10 0 m e r
Cambio de notación: R1=r, R2=R=5R1.
Potencial del sistema en r= R2 V(r= R2) = 0 (V(r) para r > R2 es el correspondiente al que crea
una carga puntual, pero con valor Q=-q+q=0, por tanto el campo eléctrico es nulo, en el infinito y
para r<R2)
Para R1 < r < R2
r
el campo vale E (r ) 
r
V (r )  V ( R2 )    E.dl   
R2
R2
q
4 0 r 2
q
4 0 r 2
dirigido radialmente hacia el centro
dr  V (r )  0  
q
4 0 r

q
4 0 R2
 V (r ) 
q  1 1 
 

4 0  r R2 
Comprobamos que efectivamente el potencial es positivo para R 1 < r < R2
La energía potencial eléctrica que tendrá el electrón en la esfera interior será: U(R1) =-eV(R1)
Igualando a la energía cinética inicial:
 eq  1
1  1
     me v 2
4 0  R1 R2  2
v
eqR2  R1 
eq5R1  R1 
eq4 R1 
eq  1
1 
   


2
2 0 me  R1 R2 
2 0 me R1 R2
2 0 me 5R1 R1
10 0 me R1
vmin
2eq
2eq

5 0 me R1
5 0 me r
Física II para Licenciaturas de Física y Matemática
5) En el circuito mostrado en la figura, ¿cuánto vale la
diferencia de potencial entre los puntos d y e: Vd -Ve ?
a) 8V
b) -8V
c) 5 V
d) -5V
e) 6 V
f) 4V
Resistencia equivalente a los en paralelo entre los
puntos d y e: RE 
R1 R2
3  6 18

  2
R1  R2 3  6 9
Consideremos las siguientes dos mallas: la a-b-e-f y la b-c-d-e, y consideremos respectivamente
las corrientes i1 e i2 que circulan respectivamente por dichas mallas en sentido horario.
Malla 1 (a-b-e-f): 18V= 12 i1+ 6(i1- i2)= 18 i1- 6 i2  i1 
18  6i2
i
 1 2
18
3
Malla 2 (b-c-d-e): 21V= 2 i2+ 6(i2- i1)+3 i2= 11 i2- 6i1 21  11i 2  61 

27
27  9i 2   i 2 
 3A
9
i
3
i1  1  2  1   2 A
3
3
Vd-Ve=3A(2) = 6V
Vd-Ve= 6V
i2 
  11i2  6  2i2
3
6) Un capacitor de capacidad C, se carga con una carga Q. Este
capacitor se conecta a otro capacitor de capacidad 3C, inicialmente
descargado y a una resistencia R como se muestra en el circuito de la
figura.
Se cierra el interruptor y se espera a que alcance el sistema alcance el
equilibrio. ¿Cuánto vale la energía total disipada en la resistencia?
a) 0
Q2
b)
8C
Q2
c)
2C
3Q 2
d)
8C
Q2
e)
4C
3Q 2
f)
32C
La energía total disipada en la resistencia es igual a la diferencia de energías almacenadas en los
capacitores. Inicialmente, la energía se acumula en el capacitor C que tiene una carga Q: U 0 
Q2
2C
Al cerrarse el circuito, la carga se redistribuye hasta que se iguala el potencial. Sean Q1 la carga final
del capacitor C y Q2 la 3C.
La carga se conserva: Q  Q1  Q2 y se igualan los potenciales: V1 
Q  Q1  Q2  Q1  3Q1  4Q1
2
U F  U1  U 2 
2
 Q1 
2
Q
4
2
 Q2 
2
Q1
Q
 V2  2
C
3C
3Q
4
2
2
Q1
Q
Q
9Q
12Q1
2Q
Q2
2 Q
 2  1  1 
 1    
2C 2(3C ) 2C
6C
6C
C
C4
8C
Finalmente la energía disipada es igual a la variación de energía: E  U 0  U F 
E
3Q 2
8C
 Q2  3Q1
Q 2 Q 2 3Q 2


2C 8C
8C