1 UCA/FCFMeI - Física II, 2do.Cuat/2010, 1er.Parcial, 2 de Octubre

1
UCA/FCFMeI - Física II, 2do.Cuat/2010, 1er.Parcial, 2 de Octubre 2010, 8:00 – 12:00 hs
COMPLETAR ENSEGUIDA
Apellido y nombre
Registro
PRO 1
PRO 2
PRO
TEO
LAB
Comisión
Firma
NOTA
Corrigió
SUMA
Problemas. Dos ejercicios: valor 50 pts.; mínimo para aprobar 25 pts. Transcriba resultados,
fórmulas y valores numéricos, en las casillas indicadas. En los espacios reservados es
obligatorio anotar una breve justificación de cada paso. Los valores numéricos deben darse
sólo con cifras significativas y con unidades. Fórmulas, números ilegibles o justificación
omitida, se consideran parte no resuelta del ejercicio y no dan puntaje. Se contesta usando los
datos: el empleo de incógnitas no es respuesta válida. Resumen de instrucciones y fórmulas de
uso frecuente están en la última página.
Problema 1: Determinación de la densidad volumétrica de carga. Se tiene una placa de
dieléctrico de sección cuadrada de lado L y espesor muy delgado d, tal que d << L.
Puede suponerse entonces que se trata de una placa plana infinita, y que solamente es
necesario tener en cuenta la dirección perpendicular a la misma, que se indica con x en
la figura. Con la finalidad de determinar la distribución de carga eléctrica en el interior
de la placa, se mide el potencial eléctrico en todo el espacio y se establece que el mismo
tiene la forma (V0 es una constante positiva con unidades de volts):
V(x) =
-d/2
- V0 π ( x/d -1/2)
d/2 < x
V0 cos( π x /d )
-d/2 < x < d/2
- V0 π ( -x/d -1/2)
x < -d/2
0
d/2
x
2
P1a) Determine el campo eléctrico E = E(x) i y grafique V(x) y E(x)
+V0 π/d
d/2 < x
[V0 π/d ] sen( π x /d )
-d/2 < x < d/2
E(x) =
-V0 π/d
x < -d/2
E(x)
V(x)
V0 π/d
V0
x
-d/2
d/2
-d/2
x
d/2
-V0 π/d
Justificación:
Se tiene E(r) = E(x) i , con E(x) = -dV(x)/dx. Para d/2 < x, E(x) = V0 π/d. Para -d/2 < x
< d/2 , E(x) = -V0 [- sen( π x /d )] π/d = [V0 π/d ] sen( π x /d ). Para x < -d/2, E(x) = V0 π/d . Se observa que tanto V(x) como E(x) son funciones continuas. La primera debe
serlo siempre, y la continuidad de E(x) indica que no hay densidades de carga
superficiales en x=d/2 y x=-d/2. V(x) es una función par de x y E(x) una función impar.
P1b) Determine y grafique la densidad de carga eléctrica volumétrica ρ(x) en todo
punto del espacio. Sugerencia: aplique la Ley de Gauss a una superficie Gaussiana con
forma de placa cuadrada de lados L paralelos a los de la lámina de dieléctrico y
espesor infinitesimal dx en la dirección x, ubicada entre los puntos x y x+dx.
0
ρ(x) =
d/2 < x
ε0 [V0 π2/d2 ]
cos( π x /d )
-d/2 < x < d/2
3
0
ρ(x)
ε0 V0π2/d2
x < -d/2
-d/2
d/2
Justificación:
Aplicando la Ley de Gauss a la superficie propuesta, tenemos AE(x+dx) –AE(x) =
ρ(x) A dx / ε0 , donde A es una superficie perpendicular a x. Aproximando E(x+dx) E(x) = (dE(x)/dx) dx se tiene dE(x)/dx = ρ(x) / ε0 , de donde ρ(x) = ε0 dE(x)/dx. Para
d/2 < x y x < -d/2, ρ(x) = 0. Para -d/2 < x < d/2 , ρ(x) = ε0 [V0 π2/d2 ] cos( π x /d ). Se
observa que ρ(x) es una función par y continua.
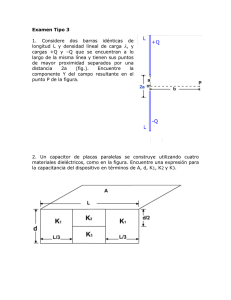
Problema 2. Capacitor de placas paralelas vertical. Se tiene un capacitor de placas paralelas
cuadradas de lado L y de distancia d entre las placas. El mismo se carga conectándose a una pila
de f.e.m. V y luego se lo desconecta de la pila, permaneciendo aislado. Luego se lo coloca en
forma vertical, como se muestra en la figura, de modo que el extremo inferior quede siempre en
contacto con la superficie horizontal de un líquido de constante dieléctrica κ. La superficie del
líquido coincide con el eje x ( y = 0) y las placas del capacitor están ubicadas paralelamente al
eje y, en x = 0 y x = d, extendiéndose ambas desde y= 0 hasta y = d (ver figura).. En estas
condiciones, el líquido es atraído hacia el interior del capacitor por fuerzas eléctricas. El
propósito de este problema es determinar la fuerza atractiva y establecer el nivel de altura
máxima al que asciende la columna de líquido entre las placas del capacitor. Por simplicidad
suponga que puede tratarse al líquido como si fuese un sólido, aunque la situación real es más
compleja.
y
d
L
0
y
x
líquido de constante κ
P2a) Calcule la energía potencial electrostática del capacitor UC(y) como función del nivel de la
altura y al que llega el líquido dentro del capacitor (y > 0). Exprese su respuesta en términos del
4
cociente UC(y) / UC(0) (cuando no hay líquido entre placas) La respuesta debe expresarse en
términos de los datos del problema (κ, L, d,V) y constantes universales.
UC(y)/ UC(0) = 1/[ 1 + (κ-1)y/L ]
Justificación:
El capacitor equivalente que se forma cuando el líquido ha ascendido una altura y está formado por
dos capacitores en paralelo, el superior de capacidad ε0 L(L-y)/d y el inferior de capacidad κε0
Ly/d, por lo que C(y) = ε0 L(L-y)/d + Ly/d es la capacidad total. En términos de la capacidad
del capacitor vacío C0 = ε0 L2/d =C(0) se tiene C(y) = C0 [ (L-y)/L + κy/L ] = C0 [ 1 + (κ-1)y/L
]. La carga constante del capacitor Q= C0 V, y la energía es UC(y) = Q2/(2 C(y)). El cociente
UC(y)/ UC(0) = C(0)/C(y) = 1/[ 1 + (κ-1)y/L ] . Para futura referencia escribimos UC(y) = UC(0)/[
1 + (κ-1)y/L ] con UC(0) = C0 V2/2 = ε0 L2 V2/(2d), es decir UC(y) = [ε0 L2 V2/(2d)] 1/[ 1 + (κ1)y/L ].
P2b) Encuentre la altura de equilibrio h a la que llega la columna de líquido entre las placas del
capacitor y exprese su respuesta en términos de h/L. Para ello calcule la fuerza eléctrica del
capacitor sobre la masa de líquido entre las placas, usando el resultado de P1a). Suponga que δ
es la densidad de masa del líquido y que la altura h es muy pequeña h << L . (Sugerencia: F = dU/dy , y (1+u)-2 ≈ 1-2u para |u|<< 1 ). La respuesta debe expresarse en términos de los
datos del problema (κ, δ ,L, d,V ) y constantes universales. Para el caso κ = 51, δ = 9 gr/cm3
, V = 1 KV, d = 1 mm, L= 10 cm exprese su resultado en forma numérica.
En forma numérica:
En fórmulas:
h/L = 1/{2[(κ-1) + δ d2 Lg /( ε0 (κ-1) V2)]}
h/L ≈ 1/140 ≈ 7.14*10-3
Justificación:
F(y) = -d UC(y)/dy = - [ε0 L2 V2/(2d)] {-1/[ 1 + (κ-1)y/L ]2}(κ-1)/L =
[ε0 (κ-1)L2 V2/(2Ld)] 1/[ 1 + (κ-1)y/L ]2 .
Si y/L << 1, F(y) ≈ [ε0 (κ-1)L2 V2/(2Ld)] (1 -2 (κ-1)y/L) . Esta fuerza debe ser equilibrada por el
peso del líquido entre las placas P(y) = mg = δ y d Lg para un valor y = h, e imponiendo la condición
2 2
F(h) = P(h) tenemos [ε0 (κ-1)L V /(2Ld)] (1 -2 (κ-1)h/L) = δ h d g L y dividiendo ambos miembros
2
2
por L , queda: [ε0 (κ-1) V /(2Ld)] (1 -2 (κ-1)h/L) = δ d h/L de donde
[ε0 (κ-1) V2/(2Ld)] = [ε0 (κ-1) V2/(2Ld)] 2 (κ-1)h/L + δ d h/L = {[ε0 (κ-1)2 V2/Ld] + δ d g}h/L y
entonces h/L = [ε0 (κ-1) V2/(2Ld)]/ {[ε0 (κ-1)2 V2/Ld] + δ d g} = 1/{2(κ-1) + 2 δ d2 Lg / (ε0 (κ-1)
V2)}.
Alternativamente, se puede resolver minimizando la energía potencial total U(y) = UC(y) + Ug(y),
donde Ug(y) = mgy (eligiendo el cero de energía potencial gravitatoria en y=0), o sea Ug(y) = δ d L g y2 ,
de modo que U(y) = [ε0 L2 V2/(2d)] 1/[ 1 + (κ-1)y/L ] + δ d L g y2 , y la ecuación dU(y)/dy=0 es la
misma que la de equilibrio de las fuerzas planteada antes.
Valor numérico:
h/L= 1/{2[50 + (9*103 Kg/m3)(10-6 m2)(10-1 m)(9.81 m/s2)/[(8.85*10-12 F/m)(50)(106 V2)] } =
h/L = 1/{2[50 + (9*9.81/(8.85*50))10(3-6-1+6) ]} = 1/{2[50 + 0.199*102]} ≈ 1/{2[50+20]}= 1/140 ≈
7.14*10-3 . Vemos que la hipótesis hecha (h/L << 1) se cumple.
===================================================================
========
Teoría: Marque la casilla con la respuesta correcta. Para aprobar teoría debe contestar por lo
menos dos preguntas. Las respuestas deben ser justificadas. Sin justificación no tienen valor.
Escala de puntaje, 4 bien = 30 ptos., 3 bien = 24 ptos., 2 bien = 15 ptos.; mínimo para
aprobar 15 ptos.; no se asigna puntaje a menos de dos aciertos.
5
Ta) Dipolo eléctrico: El momento dipolar de la molécula de agua (H2O) es de 6.17x10-30
Cm. Considere una molécula de agua situada en el origen, cuyo momento dipolar p
apunta en la dirección +x. Un ión cloruro (Cl-) de carga q = -e está situado sobre el eje x
a una distancia de 3*10-9 m de la molécula de agua. Esta distancia x es mucho mayor
que la separación entra las dos cargas puntuales que puede suponerse que forman el
dipolo, por lo que puede usarse una expresión aproximada para grandes distancias del
campo eléctrico del dipolo. La fuerza eléctrica que la molécula de agua ejerce sobre el
ión cloruro es(Sugerencia: el potencial del dipolo se puede obtener a partir del de dos
cargas puntuales) :
p
q
x
1.
N
F = 3.28*10-13
2.
F = 2.57*106 N
3.■ F = 6.57*10-13
N
4.
F = 1.2*10-4 N
Justificación
La fuerza sobre la carga q es F = qE donde E es el campo eléctrico debido al dipolo. Si el
dipolo está formado por una carga Q en x=d/2 y una carga –Q en x=-d/2 (de modo que p=Qd i),
el potencial del mismo sobre el eje x es V(x) = kQ[1/|x-d/2| - 1/|x+d/2| ] (principio de
superposición). Para x > >d/2, usando que 1/(1+u) ≈ 1-u (para |u|<<1), V(x) ≈ kQ[ (1+d/(2x))/x
-(1-d/(2x))/x ] = kQd/x2 = kp/x2 . El campo eléctrico sobre el eje es E(x) = -dV(x)/dx i = 2kp/x3
i . La fuerza es F = -2ekp/x3 i, es decir que es atractiva. Su magnitud es F = 2(1.6*10-19
C)(8.99*109 Nm2/C2)(6.17*10-30 Cm)/( 3*10-9 m )3 = (2*1.6*8.99*6.17/27)*10(9-30-19+27) N
= 6.57*10-13 N .
Tb) Péndulo eléctrico: Una pequeña esfera de 1.5 g de masa cuelga de un hilo entre dos
placas verticales paralelas separadas por una distancia de 5 cm. Las placas son de
material aislante y tienen densidades de carga superficiales uniformes de + σ y – σ . La
carga de la esfera es q = 8.9 µC. La diferencia de potencial entre las placas que hace que
la esfera forme un ángulo de 30º con la vertical es:
1.
4.77 V
2.
41.3 V
3.
23.8 V
4. ■ 47.7 V
30º
5 cm
6
Justificación
Elegimos un eje x horizontal y otro y vertical. Si θ es el ángulo del péndulo con la vertical, el
equilibrio de las fuerzas sobre la masa colgante implica dos ecuaciones: sobre x: qE = T senθ y
sobre y T cosθ = mg, (E es el campo eléctrico entre placas y m la masa de la esferita) y haciendo
el cociente entre ambas se obtiene tg θ = qE/(mg) y como E=V/d (d es la distancia entre placas)
se tiene V = (dmg tg θ)/q. Reemplazando por los datos, V = (5*10-2 m)(1.5*10-3 Kg)(9.81
m/s2)(1/√3)/(8.9*10-6 C) = (5*1.5*9.81)/(8.9*√3) 10 V = 47.7 V .
Tc) Energía electrostática: Se tiene una esfera de material dieléctrico de radio R con una
carga total Q uniformemente distribuída en su interior. El cociente entre la energía
contenida en el campo eléctrico interior de la esfera y la energía contenida en el campo
eléctrico exterior a la esfera es : (Sugerencia: el elemento de volumen es 4πr2dr con r la
coordenada radial) :
Uinterior
= 1/ 4
Uexterior
Uinterior
=2
2.
Uexterior
Uinterior
3.
= 1 / 4π
Uexterior
Uinterior
= 1/ 5
4 ■
Uexterior
1.
Q
R
Justificación
Sea ρ = Q/(4πR3/3) la densidad constante dentro de la esfera. Por simetría, el campo eléctrico es
radial y solo depende de la coordenada r: E(r) = E(r) er donde er es el versor radial. Aplicando
la Ley de Gauss a una superficie Gaussiana esférica de radio r, tenemos 4πr2 E(r) = QS/ε0 ,
donde QS es la carga encerrada por S, de modo que QS = Q si r > R, y QS = ρ4πr3/3 si r < R. La
componente radial del campo eléctrico es E(r) = kQ r /R3 si r < R y E(r) = kQ /r2 si r > R, con
k=1/(4π ε0) . La densidad de energía es ue = ε0 E2/2 de modo que ue = ε0 k2Q2r2/(2R6) si r <
R y ue = ε0 k2Q2/(2r4) si r > R. El elemento de volumen es 4πr2dr por lo que Uinterior = ∫ ε0
k2Q2r2/(2R6) 4πr2dr (entre 0 y R) y Uexterior = ∫ ε0 k2Q2/(2r4) 4πr2dr (entre R e ∞).
Calculando las integrales se obtiene Uinterior = kQ2/(10R) y Uexterior = kQ2/(2R).
Finalmente, Uinterior/ Uexterior = 1/5 .
Td) Potencial electrico: Se tiene una esfera conductora de radio R con una carga total Q.
Se rodea la misma con un cascarón esférico conductor concéntrico con la esfera y de
radio 2R. El espesor del cascarón es despreciable y el mismo se encuentra conectado a
tierra. El potencial de la esfera toma un valor V, diferente al valor V0 que tenía antes de
colocar el cascarón. La variación relativa del potencial ∆V/V0 = ( V - V0 ) / V0 es:
1. ∆V/V0 = +1/2
2. ■ ∆V/V0 = -1/2
3. ∆V/V0 = +1/4
4. ∆V/V0 = -1/4
7
2R
Q
R
Justificación:
El potencial de la esfera de radio R antes de colocar el cascarón es V0 = kQ/R. Al
colocar el cascarón, la conexión a tierra provee una carga Qind sobre el cascarón, que se
reparte entre las caras interior y exterior del mismo. Sin embargo, la carga exterior debe
ser cero ya que la diferencia de potencial entre el infinito y la cara exterior es cero, y a
su vez la misma debe ser proporcional a esa carga etxrior. La carga interior entonces es
–Q. El campo eléctrico entre la esfera y la cara interna del cascarón es entonces (usando
la ley de Gauss) idéntico al de una carga puntual, es decir puramente radial con
componente E(r) = kQ/r2 . La diferencia de potencial V(2R) –V(R) = - ∫E(r)dr (entre R
y 2R), es decir V(2R) –V(R) = kQ(1/(2R)-1/R) pero V(2R)= 0, por lo que V(R) = V =
kQ/(2R) y finalmente ∆V/V0 = ( V - V0 ) / V0 = [kQ/(2R) - kQ/R]/[ kQ/R] = -1/2 .
LABORATORIO
1. Para establecer la relación funcional entre la diferencia de potencial aplicada a una
resistencia y la intensidad de la corriente que circula por ella, se tomaron un
conjunto de pares de valores que se transcriben en la siguiente tabla.
8
x
y
xy
x²
I
V
mA
V
10
6,0
60
100
20
9,0
180
400
30
14,5
435
900
40
22,0
880
1600
50
25,0
1250
2500
Σ
150
76,5
2805
5500
Asumiendo que esa relación es lineal se le pide determinar por cuadrados mínimos la
ecuación que la representa. Si lo prefiere puede asumir que la ordenada al origen de la
función es igual a 0. Indique qué representa la pendiente de la recta hallada y qué
unidad tiene. Justifique las respuestas.
Ecuación
V(V) = 0,51(kΩ) I (mA)
nΣxy − ΣxΣy 5 × 2805 − 150 × 76,5 2550
=
=
= 0, 51
nΣx ² − (Σx)²
5 × 5500 − (150)²
5000
Σx ² Σy − ΣxΣxy 5500 × 76,5 − 150 × 2805
b=
=
=0
nΣx ² − (Σx)²
5 × 5500 − (150)²
a=
Justificación
(como obtuvo la
ecuación)
si asumen b = 0
a=
Que representa la
pendiente
Σxy 2805
=
= 0,51
Σx ² 5500
La resistencia
Que unidad
tiene
kΩ
2. Para determinar la constante eléctrica de un vidrio de 4mm se usó el capacitor plano
de placas circulares de 25,5cm de diámetro y resultó ser κ=4,1. Se le pide,
asumiendo que los valores de capacidad medidos se corresponden con los teóricos,
indique cuáles fueron sus medidas. Qué error absoluto tienen asociado si se hicieron
con un capacímetro cuyo error absoluto es 1%+2d y su apreciación 0,1pF. Exprese
los valores con la cantidad de cifras significativas pertinentes.
9
Capacidad
error absoluto
error relativo
Co
113,0
pF
1,3
pF
1,18
%
Ck
463,3
pF
4,8
pF
1,04
%
Justifique cálculo de C
A
π × (25,5 × 10−4 )²
= 8,85 ×10 −12 ×
= 113, 0 pF
d
4 × 10−3
Cκ = κ × Co = 4,1× 113, 0 = 463,3 pF
Co = ε o
Justifique cálculo de ∆C
∆C = % × medida + dígitos × apreciación
∆Co = 1% x113, 0 + 2 x0,1 = 1,1 + 0, 2 = 1,3 pF
∆Co = 1% x 463,3 + 2 x0,1 = 4, 6 + 0, 2 = 4,8 pF
Justifique cálculo de ε C
εo =
∆Co 1,3
=
x 100 = 1,18%
Co 113
εk =
4,8
∆Ck
=
= 1,04%
Co
463,3
3. En el práctico de campo eléctrico, los resultados de la variación del potencial entre
los electrodos sobre la recta que une sus centros, se muestran en el gráfico siguiente.
Asumiendo que dicha variación fuera lineal, indique sobre el mismo gráfico cómo
se modifica la función cuando agrega un cilindro macizo de 4 cm de radio centrado
en x = 16 cm y cuál es el potencial de dicho conductor. Indique por qué razón si en
lugar de un cilindro conductor macizo se pone un cilindro conductor hueco, el
resultado es el mismo. Tenga en cuenta que la diferencia de potencial entre los
conductores extremos no varía. Justifique las respuestas
10
V en función de x
V (V)
12
10
8
6
4
2
0
0
2
4
6
8
10 12 14 16 18 20 22 24
x (cm)
Justificación
Antes de colocar el cuerpo: Vo(x=12)= 6V y Vo(x=20)= 2V
Después de colocar el cuerpo:
Vo(x=12)-Vcuerpo= Vcuerpo-Vo(x=20)
Vcuerpo=1/2(Vo(x=12)+Vo(x=20)