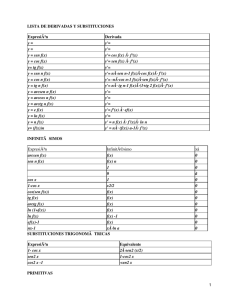
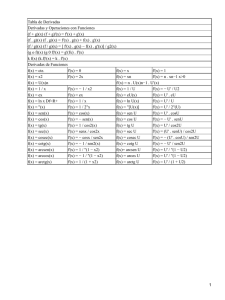
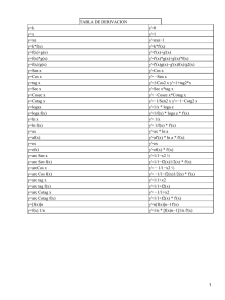
Derivadas Y=x3+2x2−x+6+4/x y'=3x2+4x−1−4/x2 Y=(x2−x)/(x+1) y'=(x2+20−1)/(x+1)2 Y=ex(x2−2x+5) y'=ex(x2+3)

Derivadas
• Y=x3+2x2−x+6+4/x y'=3x2+4x−1−4/x2
• Y=(x2−x)/(x+1) y'=(x2+20−1)/(x+1)2
• Y=ex(x2−2x+5) y'=ex(x2+3)
• Y=("x)/(x+1) y'=(1−x)/(2"x(x+1)2
• Y=(ln x)/x y'=(1−lnx)/x2
• Y= cosh +3senx y'=−senx+3cosx
• Y=(3x−2)cosh y'=3cosx −(3x−2)senx
• Y=(x2−6x)81 y'=(2x−6)(x2−6x)8081
• Y=e4x)2−(2x+1)2 y'= e4x)28x −8x−4
• Y=(ex −e−x)/(1+4e2x) y'= (13 ex4 e3x+ e−x)/ (1+4e2x)2
• Y=x/"(1−x) y'=(2−x)/2(1−x)"(1−x)
• Y=ln 4"(x2−1) y'=x/2(x2−1)
• Y=ln (x/(x+1)) y'=1/x(x+1)
• Y=2sen2x+3sen3x y'=4cos2x+9cos3x
• Y=sen3 x y'=3sen2xcosx
• Y=sen x3 y'=3x2cos x3
• Y=cos(1/x) y'=sen(1/x)/x2
• Y=(x−2)(3−x) y'=−2x+5
• Y=(2x3+1)(7x−1) y'=56x3−6x2+7
• Y=(x−1)/(x+1) y'=2/(x+1)2
• Y=(2x2−4x+2)/(x−1) y'=2
• Y= 3"x2 + 4"x3 y'=2/33"x + 3/44"x3
• Y=(x+1)ln x y'=(x+1)/x + ln x
• Y=x + arccos x y'=1−(1/"(1−x2))
• Y=x2senx y'=2xsenx + x2cosx
1