Curso 10/11 (Segundo Parcial)

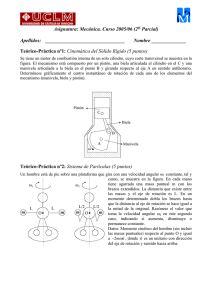
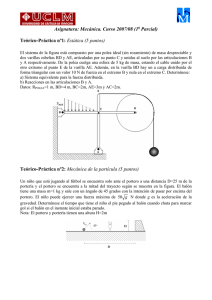
Mecánica. Curso 2010/11 (2o Parcial)
Teórico-Práctica nº1: Cinemática del Sólido Rígido (5 puntos)
Calcular gráficamente el CIR de los 7 sólidos. Utilizando dichos CIR y conociendo que la velocidad
angular del sólido 1 es 1, calcular las velocidades angulares de los sólidos restantes en este
instante. Datos: EA = R; ED = 2R; CD = R; BF = 2R; GH = R; AB= 2R
Mecánica. Curso 2010/11 (2o Parcial)
Teórico-Práctica nº2: Sistemas de partículas (5 puntos)
El sistema de la figura se compone de una varilla de longitud 4L en la dirección del eje Z apoyada
en dos articulaciones. Perpendiculares a esta varilla hay dos varillas más: la varilla 1 perpendicular
en dirección X y de longitud 2d se encuentra a una distancia L de la articulación superior, mientras
que la varilla 2 perpendicular en dirección Y y de longitud 4d se encuentra a una distancia L de la
articulación inferior. Todas las varillas son esbeltas y existen cuatro masas puntuales de masa m. En
el instante inicial representado en la figura, el sistema gira con velocidad angular i, las masas 1a y
1b se encuentran a una distancia d/2 del eje Z, y
las masas 2a y 2b a una distancia 2d del eje Z.
Después, las masas se desplazan con las
velocidades relativas indicadas. Pasado un
determinado tiempo, las masas 1a y 1b han
recorrido una distancia d/2 (llegando al
extremo) mientras que las masas 2a y 2b han
recorrido una distancia d. Calcular:
a) Momento cinético total en un instante
cualquiera respecto al punto O (en el centro de
la varilla vertical)
b) Velocidad angular del sistema en el instante
final.
Problema nº1: Mecánica del sólido
rígido (10 puntos)
Se tiene una máquina compuesta por 2 ejes paralelos accionados por una correa de transmisión. El
eje del motor gira con velocidad angular 1, se apoya en los rodamientos A y B, y está instalada la
polea 1 que se puede asimilar a un disco de radio R/2 y masa m. El segundo eje está apoyado en los
rodamientos D y E accionado por la polea 2 de radio R y masa despreciable y un rotor de forma
cilíndrica de masa 100m y radio R que gira con velocidad angular 2. El tensor de inercia del rotor
en su centro de masas es IG, donde R es el radio del cilindro y L es su longitud. En la figura se
muestran las dimensiones geométricas de la máquina. Si el rotor arranca desde el reposo hasta una
velocidad angular de 40rad/s en 10s determinar:
1) Dibujar los ejes de referencia según la expresión del tensor IG, razonando el resultado en
función de simetrías del rotor (recordar simetrías de cilindro).
2) Momento cinético del eje 2 en el centro de masas del rotor.
3) Diferencia de tensiones entre la tensión superior e inferior que tiene la correa de la polea.
4) Momento cinético del eje 1 en el centro de masas de la polea 1.
5) Potencia, par y velocidad máxima de giro que debe tener el motor para cumplir las
especificaciones marcadas.
6) Reacciones en los rodamientos del motor.
 R 2  L2
1

IG 
M rotor
 0
16
 0
0
2
0


0

2
6 R 
0
R L
2