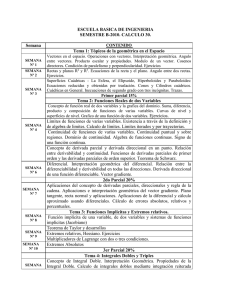
Programa Cálculo III <67KB>

UNIVERSIDAD DEL VALLE
FACULTAD DE CIENCIAS
DEPARTAMENTO DE MATEMATICAS 1
PROGRAMAS
(052CIII2010)
Prof. DORIS HINESTROZA
Cálculo III
(111052M) (Opción Científico Tecnológico) (5 horas/semana)
(3 créditos)
(Prerrequisito: Cálculo II (111051M) Aprobada, Álgebra Lineal (111048M) Aprobada).
Objetivos Generales:
1. Establecer los conceptos fundamentales del Cálculo diferencial e integral de las funciones
vectoriales y de las funciones de varias variables, las integrales de línea y de superficie.
2. Capacitar al estudiante para manejar con destreza las técnicas propias del Cálculo en varias
variables y sus aplicaciones a la resolución de problemas.
Contenido
Unidad 1: Funciones Vectoriales.
Funciones vectoriales. Operaciones algebraicas. Limites, continuidad, derivada e integral de
funciones vectoriales. Vector Tangente y Normal. Vectores velocidad y aceleración. Longitud de
curvas. Componentes tangencial y normal de la aceleración. Curvatura.
Unidad 2: Campos vectoriales y campos escalares.
Campos vectoriales y campos escalares. Curvas y superficies de nivel. Superficies: cilindros,
superficies de revolución, superficies cuadráticas. Limite y continuidad de campos escalares.
Derivada direccional, derivadas parciales. Interpretación geométrica. Derivada total. Superficies
parametrizadas. Gradiente de un campo escalar. Regla de la cadena para campos escalares.
Recta normal y plano tangente a una superficie. Derivada de campos vectoriales. Forma matricial
de la regla de la cadena.
Unidad 3: Aplicaciones de las Derivadas Parciales.
Derivada de una función dada en forma implícita. Máximos y mínimos, puntos de silla. Formula de
Taylor de orden dos para campos escalares. Matriz Hessiana. Criterio de la segunda derivada para
extremos de funciones de dos variables. Multiplicadores de Lagrange.
Unidad 4: Integrales de Línea e Integrales Múltiples.
Integrales de línea. Trabajo, circulación y flujo como ejemplos de campos vectoriales.
Independencia de trayectorias, funciones potenciales y campos conservativos. Integrales dobles.
La integral doble en coordenadas polares. Áreas, momentos y centro de masa. Integrales triples en
coordenada rectangulares. Cambio de variable en una integral triple, coordenadas cilíndricas y
esféricas. Masas y momentos en tres dimensiones.
Unidad 5: Integrales de Superficie.
Teorema de Green en el plano. Área de superficie e integrales de superficie. Superficie
parametrizada. Teorema de Stokes. El teorema de la divergencia.
Método de Trabajo.
El curso se hará en modalidad de clases magistrales y talleres. En el taller se discutirán, con la
supervisión del profesor, la solución de los problemas previamente asignados por el profesor.
Evaluación:
Porcentaje
Fecha
Exámenes cortos
40%
Trabajo en los talleres
20%
Examen Final
40%
SEMANA 16
Texto:
Cálculo con Geometría Analítica, Edwards y Penney. 4ª Edición. Editorial Prentice Hall. 1996.
Notas de Clase de Cálculo III y Guías de estudio, Profesores Doris Hinestroza y Diego Hoyos.
Bibliografía:
1. Cálculo y Geometría Analítica. Vol II. Sherman K. Stein, Anthony Barcellos. McGraw-Hill, 5ª
Edición. 1997.
2. Cálculo Vectorial. Marsden – Tromba. Editorial Addison- Wesley. 3ª Edicion.
3. Cálculo con Geometría Analítica. Louis Leithold. Editorial Harla, 7ª Edición. 1998.
4. Cálculo. Vol II, Tom Apóstol. Editorial Reverté, 2ª Edición.
5. Wesley Longman, 9ª Edición.
6. Cálculo. Vol II. Larson / Hostetler / Edwards. 6ª Edición . McGraw-Hill. 1999.
1