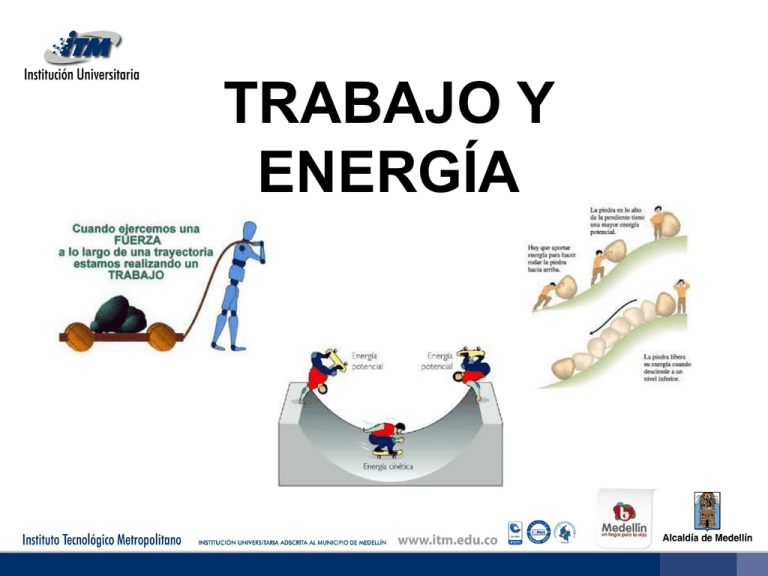
TRABAJO Y ENERGÍA

TRABAJO Y
ENERGÍA
TRABAJO Y ENERGÍA
COLISIONES
Representa un evento en el cual dos partículas
se acercan entre si e interactúan por medio de
fuerzas.
Cuando entran en contacto los objetos ejercen
fuerzas una sobre la otra de igual magnitud pero
de dirección contraria.
TRABAJO Y ENERGÍA
En colisiones se distingue 3 momentos:
• Antes
• Durante Objetos interactúan en un tiempo corto
• Después Dos objetos experimentan una fuerza
Fuerza impulsiva
Varia con el
tiempo
Gracias a ella el movimiento de los
objetos cambia y por esta razón se
puede estudiar el sistema en dos
momentos importantes, antes y
después de la colisión.
TRABAJO Y ENERGÍA
Impulso y momento lineal
Durante la colisión actúa una fuerza, si la masa
permanece constante después de la interacción y la
velocidad cambia, entonces existe una relación
entre fuerza y cambio del momento lineal del
objeto que colisiona.
El cambio del momento lineal en un intervalo de
tiempo durante el cual actúa una fuerza. Se escribe:
𝑑𝑝 = 𝐹 𝑑𝑡
TRABAJO Y ENERGÍA
Integrando la ecuación teniendo en cuenta la
duración de la colisión en los limites de integración
para el tiempo, se determina el cambio del
momento lineal
𝑝𝑓
𝑑𝑝
𝑝𝑖
= 𝑝𝑓 - 𝑝𝑖 =𝛥𝑝=
𝐼=
𝑡𝑓
𝑡𝑖
𝐹 𝑑𝑡
𝐼 =𝛥𝑝=𝑝𝑓 - 𝑝𝑖
𝑡𝑓
𝐹 𝑑𝑡
Impulso
𝑡𝑖
TRABAJO Y ENERGÍA
COLISIONES EN UNA DIMENSIÓN
La colisión es frontal, todo el movimiento se
realiza en una sola dirección.
Consideremos dos cuerpos que van a colisionar
y no existen fuerzas externas que actúen sobre
ellos, en el instante en que ocurre la colisión
cada uno ejerce una fuerza de igual magnitud
pero de sentido contrario hacia el otro.
m1
𝐹12
m2
𝐹21
TRABAJO Y ENERGÍA
Como resultado de la colisión cada partícula
sufre una variación del momento lineal.
Para m1
−𝐹12 ∆𝑡 = 𝑚1 𝑣1𝑓 − 𝑚1 𝑣1𝑖
Para m2
𝐹21 ∆𝑡 = 𝑚2 𝑣2𝑓 − 𝑚2 𝑣2𝑖
−𝐹12 = 𝐹21
𝐹12 + 𝐹21 =0
TRABAJO Y ENERGÍA
• Si 𝛥P= 0, significa que el momento lineal del
sistema es constante.
𝑝𝑖 - 𝑝𝑓
𝑚1 𝑣1𝑖 + 𝑚2 𝑣2𝑖 = 𝑚1 𝑣1𝑓 + 𝑚2 𝑣2𝑓
Esto se cumple para todo tipo de colisiones
TRABAJO Y ENERGÍA
Las colisiones se clasifican en:
• Colisiones elásticas: Si la energía cinética total es
la misma antes y después la colisión.
Se conserva el momento lineal
Se conserva la energía cinética
𝐸𝑖 = 𝐸𝑓
• Colisiones inelásticas: Si la energía cinética
cambia después de la colisión.
Estas se clasifican en perfectamente inelásticas e
inelásticas.
TRABAJO Y ENERGÍA
• Colisiones perfectamente inelásticas
Se presenta cuando los cuerpos que interactúan
quedan pegados después de la colisión.
Estos cuerpos sufren una colisión frontal, después
del choque quedan pegados y por lo tanto se
desplazaran con una misma velocidad 𝑣𝑓 .
𝑚1 𝑣1𝑖 + 𝑚2 𝑣2𝑖 = (𝑚1 +𝑚2 ) 𝑣𝑓
En esta colisión la energía no se conserva, pero si el
momento lineal.
TRABAJO Y ENERGÍA
• Colisiones inelásticas
En este tipo de colisiones no se conserva la
energía cinética del sistema de partículas. En
muchas colisiones se pierde parte de la energía
cinética, produciendo por ejemplo calor o
deformaciones en los cuerpos.
TRABAJO Y ENERGÍA
Ejercicios
1. Una pelota de 30g, que viaja hacia la derecha
a 40cm/s, choca de frente con una pelota
que esta en reposo de 60 g de masa. Si la
colisión es elástica, encuentre la rapidez de
cada pelota después de la colisión.
TRABAJO Y ENERGÍA
2. Un carro de 1700 kg de masa que lleva una
velocidad de 10 m/s choca contra otro carro de
1200 kg y que viaja a 5 m/s en direcciones
opuestas. Después del choque los dos carros
quedan unidos. ¿a que rapidez y en que
dirección se moverán?.
TRABAJO Y ENERGÍA
TAREA
1. El péndulo balístico es un dispositivo que se
utiliza para medir la velocidad de un proyectil. El
proyectil colisiona frontalmente con un cuerpo de
masa mucho mayor y queda incrustado en él. El
péndulo es un bloque de madera de masa M,
suspendido verticalmente. Un proyectil de masa m
que lleva una velocidad cuya magnitud es 𝑣𝑝 choca
con el péndulo y al penetrar el bloque de madera,
este oscila hasta alcanzar una altura H.
Calcule la velocidad del proyectil cuando choca
contra el bloque de madera.
TRABAJO Y ENERGÍA
2. Un móvil de masa m1 es empujado hacia otro
de masa m2 que esta en reposo, m1 se mueve
hacia la derecha a 0,7 m/s. Después de la
colisión m1 retrocede 0,2 m/s y m2 se mueve a
la derecha a 0,3 m/s. Luego a m1 se le adiciona
una masa de 1 kg y se empuja hacia m2 que esta
en reposo. Después de la colisión m1 queda en
reposo y m2 se mueve hacia la derecha con una
velocidad de 0,5 m/s. halle la masa de cada
móvil.