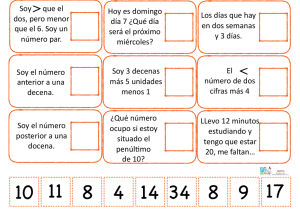
Conversión de bases exponenciales

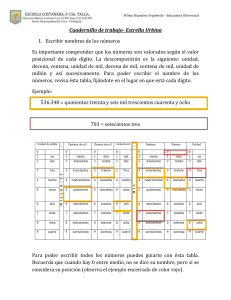
CONVERSION DE BASES EXPONENCIALES
UNIVERSIDAD PEDAGOGICA Y TECNOLOGICA DE COLOMBIA “UPTC”
TUNJA (BOYACA)
2009
INTRODUCCION
Mediante este trabajo quiero demostrar con un proceso como hacer que números
que tienen bases exponenciales sean cambiados para llegar a cualquier otra base
exponencial.
2
Como sacar un número de base 10 a otra base:
Para sacar un número dentro de cierta base podemos iniciar teniendo en cuenta dicho
número en base 10.
52(10)
Este número equivale a 52.
52(10)=52
Ahora vamos a cambiar dicho número a base 8.
52(8)
Podemos hacer un secuencia de restas que nos lleve al total de la base, cada
resta equivale a una decima y lo que sobra se produce en dígitos.
52-8=44-8=36-8=28-8=20-8=12-8=4
Tomamos el número de veces que restamos el numero por 8, en este caso 6
veces para las decenas y el sobrante en este caso 4 lo tomamos como digito,
ósea que el resultado es 64.
6(decena) 4(digito)= 64
Dando otro ejemplo, se va a tomar el mismo número 52 pero ahora en base 5, entonces:
52-5=47-5=42-5=37-5=32-5=27-5=22-5=17-5=12-5=7-5=2
En este caso el numero fue restado 10 veces por 5 y sobraron 2, pero no por esto el
resultado es 102 ¿porque? Porque el 10 de la expresión 102 no es una decena y una
centena, sino que 10 en si es la decena, lo cual no es válido en base 5, entonces 10 es
restado por 5 como en el caso anterior:
10-5=5-5=0
3
Y esto produce 2 centenas y 0 decenas a las cuales hay que agregar el digito que ya
habíamos visto era 2.
2(centena) 0(decena) 2(digito)=202
Por supuesto que los números a cambiar de base no necesariamente deben estar
inicialmente en base 10 ya que este procedimiento sirve para cambiar desde cualquier
base a cualquier base.
Formula resultante:
XR=X (m)
X-m mientras X>m=n donde n es la resultante que no se puede restar a m
XR=n veces que m fue restada de X, y n.
Simbología
XR= valor total
X= número inicial
m= base
n= resultante que no se puede restar a m
4