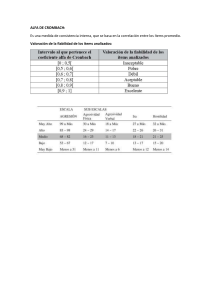
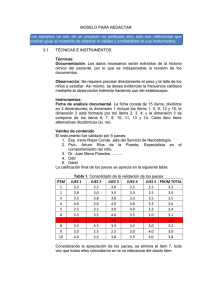
Análisis de datos cuantitativos y cualitativos UNIDAD DE POSGRADO DE LA FACULTAD DE EDUCACIÓN GESTIÓN EDUCATIVA ANÁLISIS DE DATOS CUANTITATIVOS Y CUALITATIVOS SEMANA 09,10, 11, 12 del silabo 25 y 26 de noviembre DOCENTE: Mg. HÉCTOR BASILIO MARCELO Huancayo - 2017 Mg. Héctor Basilio Marcelo 1 Análisis de datos cuantitativos y cualitativos PRUEBA DE HIPÓTESIS Una hipótesis estadística es una afirmación acerca de la distribución de cierta variable aleatoria. En dichas hipótesis se considera el valor de un parámetro correspondiente a la distribución poblacional conocida o supuestamente conocida. Una prueba estadística es un procedimiento para decidir si se rechaza o no la hipótesis estadística considerando el resultado de un experimento aleatorio. Clasificación de hipótesis Hipótesis Alterna (HA): Una hipótesis alterna (Alternativa) es una hipótesis direccional, es decir lo que se quiere comprobar en muchos casos. Ejemplo La inteligencia lógica influyen en el rendimiento académico. Hipótesis Nula (H0): La hipótesis nula es la contraparte de la hipótesis alterna en muchos caso lo que no quisiéramos que ocurra. Ejemplo: La inteligencia lógica no influye en el rendimiento académico. Prueba de hipótesis: Regla convencional para comprobar o contrastar hipótesis estadísticas: Se llama también ensayo de hipótesis o dócima de hipótesis. Son procedimientos que se usan para determinar, si es razonable o correcto, aceptar que el estadístico obtenido en la muestra, puede provenir de la población que tiene como parámetro, el formulado en H0. Aceptar H0, convenimos en que el error de muestreo (el azar), por sí solo, puede dar lugar al valor estadístico que origina la diferencia entre éste y el parámetro. Rechazar H0, convenimos que la diferencia es tan grande, que no es fruto del error de muestreo (el azar) y concluimos que el estadístico de la muestra no proviene de una población que tenga el parámetro estudiando. Procedimiento para la prueba de hipótesis: La prueba Z: La prueba Z, emplea las medias muestrales como estadístico básico. Esta prueba se utiliza cuando las muestras son más de 30 sujetos u objetos de estudio y así mismo se conoce la varianza de la población. Región crítica de Z: La región crítica para el rechazo de la hipótesis nula es el área debajo de la curva que contiene a todos los valores del estadístico que permite el rechazo de la hipótesis nula. Región de Rechazo de Ho Región de Rechazo de Ho Zt Mg. Héctor Basilio Marcelo Zt 2 Análisis de datos cuantitativos y cualitativos Valor crítico o teórico: Para analizar los datos mediante este método alternativo, basta calcular Zc, luego determinar el valor crítico o teórico correspondiente al nivel de significación α de 0,05 y 0,01. Valores de Z: 90% → Z = 1,64 95% → Z = 1,96 98% → Z = 2,33 99% → Z = 2,576 Para una población de estudio: La variable aleatoria Z se define por: Zc x x x n Si Zc Zt se rechaza la hipótesis nula. En caso contrario, la hipótesis nula se conserva. Prueba bilateral: Cuando existen dos opciones: Prueba unilateral: Cuando existe una sola opción: Ejemplo 1: El rector de cierta universidad del Perú piensa que durante los últimos años, la edad promedio de los estudiantes que asisten a esta institución ha cambiado. Para probar esta hipótesis, se realiza un experimento en el cual se mide la edad de los 150 estudiantes elegidos al azar entre todos los estudiantes de éste centro de educación superior. La edad promedio es de 23,5 años. Un censo anterior realizado en la universidad, unos cuantos años antes del experimento, reveló una edad promedio de 22,4 años, con una desviación estándar de 7,6. a) Plantear las hipótesis b) Comprobar Para dos poblaciones de estudio Para este caso seleccionamos una muestra de cada población y determinamos las medias aritméticas de cada una de ellas. La variable aleatoria Z para dos poblaciones se definirá por: I. Si: x1 x2 , entonces H0: 1 2 H1: 1 2 Por lo tanto la estadística de prueba será: Zc x1 x2 12 n1 Mg. Héctor Basilio Marcelo 22 n2 3 Análisis de datos cuantitativos y cualitativos La regla de decisión será: Si Zc Zt, rechazar H0, caso contrario no. II. Si: x1 x2 , entonces H0: 1 2 H1: 1 2 Por lo tanto la estadística de prueba será: Zc x1 x2 12 n1 22 n2 La regla de decisión será: Si Zc Zt, rechazar H0, caso contrario no. III. Si, es una investigación experimental y control, se tendrá: H0: 1 2 1 2 H1: Entonces la estadística de prueba será: Zc x1 x2 12 n1 22 n2 La regla de decisión será: Si Zc Zt, rechazar H0, caso contrario no. Ejemplo 4: Para determinar si existen diferencias estadísticamente significativas entre la agresividad de los hijos de docentes y no docentes de la UNSA, se seleccionaron muestras al azar de 50 hijos de los docentes y 60 hijos de los no docentes de la UNSA, ambos del cuarto y quinto de educación básica regular, a las que se les aplico una prueba que mide la agresividad, cuyos resultados fueron los siguientes: HIJOS x De los docentes De los no docentes 24,3 26,1 4,4 4,9 a) Plantear las hipótesis b) Utilizando α = 0,01 2 colas, ¿Cuál es la conclusión? PRACTICA 1. Un fabricante de cigarrillos publicita que la marca A no es más dañina para la salud que la marca B (con filtro). Suponiendo que el daño a la salud está asociado con el contenido de nicotina, el Ministerio de Salud tomó al azar dos muestras de cigarrillos de la marca A y de la Marca B y midió la cantidad de nicotina con la misma técnica, de donde surgieron los siguientes datos: MARA A nA = 125 MARCA B nB = 180 x A = 24,6 mg A = 1,4 mg x B = 24,3 mg B = 1,1 mg Mg. Héctor Basilio Marcelo 4 Análisis de datos cuantitativos y cualitativos Establecer las hipótesis y contrastarlos a un nivel de significación de 5% LA PRUEBA t DE STUDENT Es una prueba estadística para evaluar si dos grupos difieren entre si de manera significativa respecto a sus medias La prueba t para dos muestras independientes: Los investigadores suelen sacar dos muestras aleatorias de una población y asignarles un tratamiento experimental específico. Después de exponerlos a éste experimento, se comparan ambos grupos con respecto a ciertas características para averiguar el efecto del tratamiento. Posiblemente se observe una diferencia entre ambos grupos. Fórmula: En función a la media: X -X 1 2 t S12 S 22 N1 N 2 S12 var ianza del grupo 1 X media del grupo 1 1 En función a la r de Pearson: r N 2 t 1 r2 Ejemplo 1: A fin de determinar si existe diferencias estadísticamente significativas entre los puntajes de autorresponsabilidad de los grupos de postulantes a una universidad X; unos se prepararon en centros pre universitarios y otros se auto prepararon, se seleccionó una muestra aleatoria de 14 postulantes que se prepararon en centros pre universitarios y 12 que se preparan por su cuenta y se les aplicó un test de responsabilidad, los resultados fueron los siguientes. Postulantes 1 2 3 4 5 6 7 8 9 10 11 12 13 14 Mg. Héctor Basilio Marcelo Centro pre 20 21 20 18 22 20 19 21 19 18 20 21 17 23 Su casa 20 22 21 22 23 22 21 23 20 19 23 23 5 Análisis de datos cuantitativos y cualitativos Media C = 19,92 Media S = 21,58 Varianza = 2,66 Varianza = 1,87 Hipotesis: Ho : No existe diferencias estadísticamente significativas entre los puntajes promedios de autorresponsabilidad de los postulantes. H1 : Si existe diferencias estadísticamente significativas entre los puntajes promedios de autorresponsabilidad de los postulantes. Ejemplo 2: Una propaganda de un refresco dietético asegura que si se toma a diario y por un mes se obtendrá una pérdida de peso; la defensoría del consumidor sospecha que ésta propaganda es falsa, por lo que realiza un estudio con 12 personas dispuestas voluntariamente a llevar a cabo dicha investigación conteniéndose los siguientes resultados. Sujetos 1 2 3 4 5 6 7 8 9 10 11 12 Antes de la Después de propaganda propaganda 126 120 194 180 135 140 179 180 205 186 139 142 142 146 172 161 159 160 194 200 164 156 139 126 la Hipótesis: Ho: No existe pérdida de peso de las personas, después de tomar el refresco dietético durante el periodo de un mes. H1: Existe pérdida de peso de las personas, después de tomar el refresco dietético durante el periodo de un mes CORRELACIÓN Se llama correlación a la relación entre dos o más variables estadísticas referidas a una misma muestra. El grado de correlación entre dos variables se mide mediante los coeficientes de correlación. Ejemplos - Las calificaciones altas en una asignatura, suele corresponder calificaciones en un test de inteligencia. - El peso de las personas depende generalmente de su estatura. - El tiempo de servicios generalmente se relaciona con la edad. - El ahorro depende del ingreso - La demanda depende de los precios - El consumo depende del ingreso Clases de correlaciones: a) Correlación simple (cuando se realiza entre dos variables) b) Correlación múltiple (cuando se realiza tres o mas variables) Mg. Héctor Basilio Marcelo 6 Análisis de datos cuantitativos y cualitativos c) Correlación lineal (Cuando el diagrama de dispersión tiende a formar una línea recta) d) Correlación no lineal (cuando el diagrama de dispersión tiende a formar una curva Diagramas de dispersión: Gráfica que describe la relación entre las dos variables de interés Las variables X e Y se grafican en un plano cartesiano se puede obtener los siguientes gráficos. PROPIEDADES DE “r” o el coeficiente de correlación -1 ≤ r ≤ + 1 De donde se deduce que: Si r > 0 , entonces existe correlación directa positiva. Si r < 0 , existe correlación inversa negativa. Si r = 1 ,Correlación perfecta positiva Si r = -1 , Existe una correlación perfecta negativa Si r = 0 , las variables son incorrelacionadas. (Correlación nula) ANÁLISIS DE CORRELACIÓN Análisis de correlación: se usa un grupo de técnicas estadísticas para medir la fuerza de la relación (correlación) entre dos variables. . Variable dependiente: la variable que se pronostica o estima (y) Variable independiente: la variable que proporciona la base para la estimación. Es la variable predictoria. (x) CORRELACIÓN PRODUCTO MOMENTO O “r” DE PEARSON Es el coeficiente ideado por Kalz Pearson, estadístico inglés, y es el índice de correlación mas usado. Fórmula para r N XY-( X)( Y) r [N X 2 ( X)2 ][N Y 2 ( Y)2 ] Mg. Héctor Basilio Marcelo 7 Análisis de datos cuantitativos y cualitativos Hallar el coeficiente de correlación r de pearson de las puntuaciones originales de 14 estudiantes que obtuvieron en dos pruebas X de estadística y Y de matemática, según la siguiente tabla. X Y 18 28 18 30 17 30 X 17 26 16 28 16 24 Y 15 22 X2 15 20 14 26 14 22 Y2 13 24 13 18 12 20 12 18 XY 1 2 3 4 5 6 7 8 9 10 11 12 13 14 N Ejemplo: 1. Se realiza un estudio para establecer una ecuación mediante la cual se pueda utilizar la longitud en cm. de una cierta variedad de planta al cabo de un año de vida para predecir la longitud de esa variedad de planta en edad adulta: Longitud en cm. el primer año (x) 15,3 14,8 12,6 18,4 17,9 15,6 18,4 14,1 20,2 21,7 20,4 16,5 15,9 17,9 16,7 Longitud en cm. en edad adulta (y) 30,7 32,5 26,3 35,9 34,3 28,5 37,4 29,7 38,8 40,4 40,9 33,3 30,1 35,7 31,4 Se pide: a) Representar el diagrama de dispersión b) Calcular el coeficiente de correlación r de pearson Mg. Héctor Basilio Marcelo 8 Análisis de datos cuantitativos y cualitativos COEFICIENTE DE CORRELACIÓN POR RANGOS “ρ” La correlación por rangos se refiere a la correspondencia en el ordenamiento de los elementos de dos conjuntos dados. La fuerza de la correlación se mide por medio del coeficiente de correlación por rangos se Spearman. Cuya fórmula es: 6 D2 (1 ) 2 n(n 1) ρ: La letra griega rho, designa el coeficiente de correlación por rangos D: Diferencia de rangos correspondientes entre si pertenecientes a dos variables X y Y. Por ejemplo D = x1 – y1 n : número de pares correspondientes. Ejemplo: En la primera columna de la izquierda de la tabla se presenta un grupo de 5 estudiantes; en la segunda columna están sus niveles mentales que se consideran como categorías de la variable X, en la tercera columna se indican los resultados de un test psicotécnico aplicado al grupo, cuyas puntuaciones son valores de la variable Y. ALUMNOS Rodríguez Fernández Córdova Flores Lezama Nivel Mental X Medio Inferior al Promedio Superior al Promedio Muy superior al promedio Muy inferior al Promedio Test. Psicotécnico 35 17 48 42 20 Calcular el coeficiente de correlación por rangos. ALUMNOS Rodríguez Fernández Córdova Flores Lezama Nivel Mental X 3 4 2 1 5 Test. Psicotécnico 3 5 1 2 4 D: Diferencia 0 -1 1 -1 1 D2 0 1 1 1 1 ΣD2=4 6(4) ) 5(25 1) 0,80 (1 Ejemplo Cinco niños se someten a una prueba de habilidad mental y los resultados de ésta se ordenan por rangos en la columna X. También se muestran en la columna Y los rangos de estos mismos cinco niños respecto al tiempo que gastan en mirar TV Mg. Héctor Basilio Marcelo 9 Análisis de datos cuantitativos y cualitativos ALUMNOS A B C D E X 1 2 3 4 5 Y 4ó5 4ó5 2ó3 1 2o3 Y 4,5 4,5 2,5 0,5 2,5 ANÁLISIS DE VALIDEZ Y CONFIABILIDAD DE UN INSTRUMENTO Confiabilidad: La confiabilidad de un instrumento de medición se refiere al grado en que su aplicación repetida al mismo sujeto produce resultados iguales Hernández y otros (2008). La confiabilidad de un instrumento de medición se determina mediante diversas técnicas: Medida de estabilidad (Confiabilidad) (Tes retest) En este procedimiento un mismo instrumento de medición (ó ítems o indicadores) se aplica dos o más veces a un mismo grupo de personas, después de cierto periodo si la correlación entre los resultados de las diferentes aplicaciones es positiva, el instrumento se considera confiable. Método de formas alternativas o paralelas: En este procedimiento no se administra el mismo instrumento de medición, sino dos o más versiones equivalentes a éste. Las versiones son similares en contenido, instrucciones duración y otras características. La ventaja es que se aplica en un tiempo corto al mismo grupo, si la correlación entre los resultados de las diferentes aplicaciones es positiva, el instrumento se considera confiable. Método de mitades partidas: EL instrumento se parte en dos mitades, generalmente los reactivos pares y los reactivos impares. Luego se correlacionan, si la correlación entre los resultados es positiva, el instrumento se considera confiable. Homogeneidad del instrumento: Evalúa la homogeneidad y el grado en el cual los ítems de la prueba se intercorrelacionan entre si. Se emplea el Coeficiente Kuder Richardson cuando los ítems son de tipo dicotómicos. 2 N S p(1 p) KR ( ) N 1 S2 KR: Coeficiente confiabilidad N: número de ítems del instrumento S2: varianza total del instrumento p: porcentaje promedio de respuestas correctas. 1 – p: porcentaje promedio de respuestas incorrectas Cuando los ítems que conforman la prueba son polifónicos se utiliza: El coeficiente Alfa de Cronbach. Mg. Héctor Basilio Marcelo 10 Análisis de datos cuantitativos y cualitativos K S (1 2 i ) K 1 St 2 : coeficiente de confiabilidad Si2 : Sumatoria de varianzas individuales de cada ítem St2 : Varianza total del instrumento K : Número ítems del instrumento Importante: Los coeficientes de confiabilidad deben tener un valor mínimo de 0,60; en caso contrario hay que modificar los ítems y volver aplicar el instrumento. Baptista (2006) Validez: La validez en términos generales, se refiere al grado en que un instrumento realmente mide la variable que pretende medir. Por ejemplo, un instrumento para medir la inteligencia válido debe medir inteligencia y no la memoria. Una prueba sobre conocimientos de historia tiene que medir esto y no conocimientos de Literatura histórica. Un método para medir el rendimiento bursátil tiene que medir precisamente esto y no la imagen de la empresa. La validez es el grado en que un instrumento de medida realmente mide la variable que pretende medir. Se dice que un instrumento es válido cuando demuestra efectividad en cuanto a lo que mide. Es decir mide lo que se ha propuesto medir. Los tipos de validez pueden ser: De contenido, de criterio, de constructo. La validez de contenido: Se refiere al grado en que un instrumento refleja un dominio específico de contenido de lo que se mide. Se presenta cuando los ítems que integran el instrumento constituyen una muestra representativa de los indicadores de la propiedad que mide. La validez de criterio: Establece la validez de un instrumento de medición comparándolo con algún otro criterio externo. Este criterio es un estándar con el que se juzga la validez del instrumento. Puede ser validez predictiva; cuando la prueba es capaz de predecir un determinado rendimiento o comportamiento el cual es evaluado a través de ciertas mediciones llamadas criterios. O también Validez Concurrente; se refiere al estudio de los puntajes de las pruebas y un criterio obteniéndose los resultados simultáneamente. Por ejemplo, un cuestionario para detectar las preferencias del electorado por los distintos partidos contendientes puede validarse aplicándolos tres o cuatro días antes de la elección, y sus resultados compararlos con los resultados finales de la elección. Validez de constructo: Es probablemente la más importante, sobre todo desde una perspectiva científica, y se refiere al grado en que una medición se relaciona de manera consistente con otras mediciones, de acuerdo con hipótesis derivadas teóricamente y que conciernen a los conceptos (o Mg. Héctor Basilio Marcelo 11 Análisis de datos cuantitativos y cualitativos constructos) que están midiendo. Un constructo es una variable medida y que tiene lugar dentro de una teoría o un esquema teórico. La validez de constructo incluye tres etapas: 1. Se establece y especifica la relación teórica entre los conceptos. 2. Se correlaciona ambos conceptos y se analizan. 3. Se interpreta la evidencia empírica de acuerdo a qué tanto clarifica la validez de constructo. VALIDEZ TOTAL: V. Contenido + V. Criterio + V. Constructo Mg. Héctor Basilio Marcelo 12