Derivadas

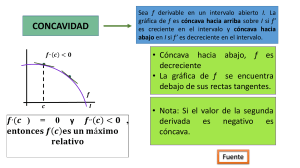
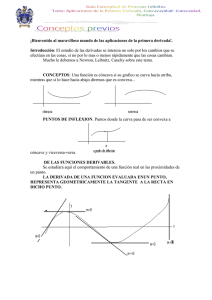
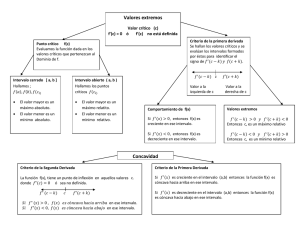
Unidad 3
1 //Escenario
Escenario25
Lectura fundamental
Fundamental
Estrategias
Etapas
de uny plan
aplicaciones
de comunicación
de las
estratégica
derivadas
Contenido
1
Aplicaciones de la derivada
Palabras clave: optimización, derivada, puntos críticos, crecimiento, decrecimiento.
1. Aplicaciones de la derivada
La información que obtenemos de la derivada puede utilizarse para analizar las propiedades de las
funciones, para solucionar variedad de problemas de optimización y para establecer si el nivel de
producción se maximiza en determinada empresa obteniendo costos mínimos. En general, la teoría
de la optimización y sus técnicas comprende un área extensa de las matemáticas aplicadas e incluye la
exploración de los "mejores valores" dada una función preliminar en un dominio definido.
En el presente escenario de aprendizaje se profundizará en las herramientas descritas anteriormente.
Se ampliará la comprensión de la primera y la segunda derivadas, desarrollaremos un método para
encontrar los valores máximos o mínimos de una función y así lograr optimizar estos procedimientos
basados en el cálculo.
1.1. Derivadas: interpretaciones
Figura 1. Relación entre f’( x ) y las funciones crecientes /decrecientes
Fuente: elaboración propia
POLITÉCNICO GRANCOLOMBIANO
2
1.2. La primera derivada
La primera derivada representa la razón de cambio instantánea en f ( x ) respecto de una modificación
en x.
En la figura 1 podemos identificar las condiciones de la pendiente, la cual está representada por la
primera derivada. Si la primera derivada de f es positiva en todo un intervalo, entonces la pendiente
será positiva y f será una función creciente en el intervalo. Pasará todo lo contrario si la primera
derivada de f es negativa a lo largo de todo un intervalo; entonces la pendiente será negativa y f será
una función decreciente en el intervalo.
Esto lo podemos sintetizar de la siguiente manera:
1.2.1.
Función creciente
Se dice que la función f es una función estrictamente creciente en un intervalo si, para cualquier x1 y
x2 dentro del intervalo, x1 < x2, implica que f ( x1) < f ( x2 ) (ver figura 1 apartado a) y b)).
1.2.2. Función decreciente
Se dice que la función f es una función estrictamente decreciente en un intervalo si, para cualquier x1
y x2 dentro del intervalo, x1 < x2 implica que f ( x1) > f ( x2) (ver figura 1 apartado c) y d)).
1.2.3. Criterios para funciones crecientes, decrecientes o constante con la primera derivada
Sea f diferenciable en el intervalo (a, b). Si f’( x ) > 0 para toda x en (a, b), entonces f es creciente en
(a, b). Si f’( x ) < 0, para toda x en (a, b), entonces f es decreciente en (a, b). Si f’( x ) = 0 para cada
valor de x en un intervalo (a, b), entonces, f es constante en (a, b).
POLITÉCNICO GRANCOLOMBIANO
3
Ejemplo 1
Para determinar los intervalos donde la función f ( x ) =
constante.
18x es creciente, decreciente o
Estimemos todos los valores de x para los que f’( x ) = 0 o f’ ( x ) es discontinua e identifiquemos los
intervalos abiertos definidos por estos números.
La derivada de:
f'( x ) = -2x2 +18 = 2(-x2 + 9) = 2 (-x + 3)(x + 3)
Encontremos los posibles puntos donde la derivada es cero para cada valor de x en un intervalo (a, b)
f'( x ) = 0
Lo que implica:
2 (-� + 3)(� + 3) = 0
Esto es válido cuando x = ±3 y con este resultado podemos dividir a la recta real en los intervalos
(-∞, -3),(-3, 3) y (3, +∞)
Para determinar el signo de f'( x ) en los intervalos anteriormente descritos, haremos uso de un valor
para x conveniente en cada uno de los intervalos. Este valor puede variar según el que se escoja, pero
en últimas en este intervalo será cierto el signo de la derivada (positivo o negativo).
Tabla 1. Intervalos para la función del crecimiento y decrecimiento
Intervalo
Punto de prueba c
f´(c)
Signo de f’(x)
Característica
(-∞,-3)
-4
2(-(-4)+3)(-4+3)=-14
-
Decreciente
(-3,3)
0
2(-(0)+3)(0+3)=18
+
Creciente
(3,+∞)
4
2(-(4)+3)(4+3)=-14
-
Decreciente
Fuente: elaboración propia
POLITÉCNICO GRANCOLOMBIANO
4
La figura 2 muestra los tramos donde la función es creciente y decreciente, y para x = ±3 no es ni
creciente ni decreciente:
Figura 2. Tramos crecientes /decreciente
Fuente: elaboración propia
En la figura 3 notamos la inclusión de unos nuevos elementos a la hora de describir una función. Estos
términos los llamaremos máximo relativo y mínimo relativo; en caso de que fueran los más altos o los
más bajos serían absolutos.
Figura 3. Mínimos y máximos relativos
Fuente: elaboración propia
POLITÉCNICO GRANCOLOMBIANO
5
1.2.4. Máximo y mínimo relativo
Una función tiene un máximo relativo para un valor de c si existe un intervalo abierto que contenga
a este valor sobre el cual f ( c ) ≥ f ( x ) para toda x en el intervalo. El máximo relativo es f ( c ). Una
función tiene un mínimo relativo para un valor de c si existe un intervalo abierto que contenga a c
sobre el cual f ( c ) ≤ f ( x ) para toda x en el intervalo. El mínimo relativo es f ( c ).
1.2.5. Máximo y mínimo absoluto
Una función tiene un máximo absoluto para un valor de c si f ( c ) ≥ f ( x ) para toda x en el dominio
de f. El máximo absoluto es f ( c ). Una función f tiene un mínimo absoluto para un valor de
f ( c ) ≤ f ( x ), para toda x en el dominio de f. El mínimo absoluto es f ( c ).
En la figura 3 observamos que P1 y P3 son máximos relativos; no son absolutos por el hecho de
que la gráfica se extiende desde (-∞, +∞) y no se tiene certeza en todo el dominio de la función.
Por otro lado, notamos un mínimo relativo en P2, el cual es el único que se logra identificar en el
tramo mostrado. A los puntos P1, P2 y P3 se les conoce como punto crítico y tienen las siguientes
características:
Si c está en el dominio de f y f’( c ) = 0 o f’( c ) no está definida, entonces c se denomina valor crítico
de f. Si c es un valor crítico, entonces el punto (c, f ( c )) se denomina punto crítico.
Note que P1 y P2 tienen una derivada igual a cero y en P3 la derivada no está definida.
POLITÉCNICO GRANCOLOMBIANO
6
1.3. Estrategias para determinar los puntos máximos y mínimos en una función
continua f
1. Determine los valores críticos de f.
2. Determine el signo de f’( x ) a la izquierda y derecha de cada valor crítico.
a. Si f’( x ) cambia de signo positivo a negativo conforme se mueve a través de un valor crítico
c, entonces f ( c ) es un máximo relativo.
b. Si f’( x ) cambia de signo negativo a positivo conforme se mueve a través de un valor crítico
c, entonces f ( c ) es un mínimo relativo.
c. Si f’( x ) no cambia de signo mientras se mueve a través de un valor crítico c, entonces f ( c )
no es un extremo relativo.
Lo anterior se puede ejemplificar para mayor claridad en la figura 4:
Figura 4. Resumen para la estrategia de máximos y mínimos
Fuente: elaboración propia
POLITÉCNICO GRANCOLOMBIANO
7
Ejemplo 2
Determinar los máximos y mínimos relativos de la función:
f ( x ) = x³- 3x²- 24x + 32
Hagamos uso de la estrategia descrita anteriormente para determinar los máximos y los mínimos
relativos:
1. Determinemos los valores críticos de f
Para encontrar estos valores hagamos uso de f'( x ) = 0, luego tenemos:
f'( x ) = 3x² - 6x - 24
Esta expresión que obtenemos la factorizamos e igualamos a cero, obteniendo:
f'( x ) = 3(x + 2) (x - 4) = 0
Luego se obtienen los valores críticos para cuando x = -2 y x = 4, y con este resultado podemos dividir
a la recta real en los intervalos (-∞, -2),(-2, 4) y (4, +∞).
Tabla 2. Intervalos para la función del crecimiento y decrecimiento
Intervalo
Punto de prueba c
f´(c)
Signo de f’(x)
Característica
(-∞,-2)
-3
3((-3)+2)(-3-4)=21
+
Creciente
-2
0
0
Máximo
0
3(0+2)(0-4) = - 18
-
Decreciente
4
0
0
Mínimo
5
2(5+3)(5+3)=450
+
Creciente
(-2,4)
(4,+∞)
Fuente: elaboración propia
En la tabla 2 queda resumida la información correspondiente a los máximos y los mínimos relativos;
notamos que pasó de un intervalo donde la pendiente es positiva a otro donde la pendiente es
negativa, luego, tenemos un máximo relativo y de manera análoga sucede para el punto mínimo
(ver figura 5).
POLITÉCNICO GRANCOLOMBIANO
8
Figura 5. Máximo y mínimos relativos
Fuente: elaboración propia
Ejemplo 3
El número de delitos graves cometidos en una determinada ciudad entre los años 1995 a 2002 es
aproximado por la función:
D( t ) = -0.1t³ + 1.5t² + 100
(0 ≤ t ≤ 7)
Donde D( t ) representa la cantidad de delitos cometidos en el año y t los años; t = 0 es el año 1995.
Determinaremos dónde la cantidad de delitos es creciente y dónde es decreciente para el intervalo de
tiempo señalado.
La derivada de D'( t ) de la función D es:
D'( t ) = -0.3t² + 3t = -0.3t(t - 10)
Esta expresión la factorizamos e igualamos a cero:
-0.3t(t -10) = 0
Luego se obtienen los valores críticos para cuando t = 0 y t = 10, y con este resultado podemos dividir
a la recta real en los intervalos (-∞, 0), (0, 10) y (10, + ∞)
POLITÉCNICO GRANCOLOMBIANO
9
Tabla 3. Intervalos para la función del crecimiento y decrecimiento
Intervalo
Punto de prueba c
f´(c)
Signo de f’(x)
Característica
(-∞,0)
-1
-0.3(-1)(-1-10)=-3.3
-
Decreciente
0
0
0
Mínimo
1
-0.3(1)(1-10)= 2.7
+
Creciente
10
10
0
Máximo
11
-0.3(11)(11-10)=3.3
-
Decreciente
(0,10)
(10,+∞)
Fuente: elaboración propia
En la tabla 3 queda resumida la información correspondiente a los máximos y los mínimos relativos.
Notamos que pasó de un intervalo donde la pendiente es negativa a otro donde la pendiente es
positiva; luego, tenemos un mínimo relativo y de manera análoga sucede para el punto máximo
(ver figura 6). Adicionalmente, para el periodo (0 ≤ t ≤ 7) vemos que nuestra función es creciente.
Pasado el periodo de 10 años, notamos un decrecimiento en los índices delictivos de esta ciudad.
Figura 6. Gráfica ejemplo 3
Fuente: elaboración propia
POLITÉCNICO GRANCOLOMBIANO
10
1.4. La segunda derivada
La segunda derivada, representada por f’'( x ), nos da cuenta de la razón de cambio instantánea de
f’( x ) respecto a x. En otras palabras, indica la tasa a la cual la pendiente de la función está variando
en relación con el cambio en x; para ello dirija su atención a la figura 7.
Figura 7. Relación entre la segunda derivada y la pendiente
Fuente: elaboración propia
En esta figura, la función se presenta en las regiones delimitadas por los diferentes colores;
se notan ciertas concavidades, es decir, tiene una parte hundida y otra pronunciada. Este tipo
de comportamiento es predecible en la medida que se cumplan una serie de condiciones.
Acontinuación, detallaremos la relación de la segunda derivada y la concavidad.
POLITÉCNICO GRANCOLOMBIANO
11
1.4.1.
Relaciones entre la segunda derivada y la concavidad
•
Si f''( x ) < 0 en un intervalo a ≤ x ≤ b, la gráfica de f será cóncava hacia abajo en ese intervalo.
Para cualquier punto x = c dentro del intervalo, se dice que f es cóncava hacia abajo en [c, f ( c)].
En la figura 7, vemos que de A hasta B y de D hasta E la función es cóncava hacia abajo.
•
Si f''( x ) > 0 en cualquier intervalo a ≤ x ≤ b, la gráfica de f será cóncava hacia arriba en ese
intervalo. Para cualquier punto x = c dentro del intervalo, se dice que f es cóncava hacia arriba
en [c, f ( c )]. En la figura 7, vemos que de B hasta D la función es cóncava hacia abajo.
•
Si f''( x ) = 0 en cualquier punto x = c en el dominio de f, no puede sacarse conclusión alguna
sobre la concavidad en [c, f ( c )].
1.4.2. Criterio de la segunda derivada para hallar máximo y mínimo de una función
Sea f una función tal que f'( c ) = 0 y la segunda derivada de f existe en un intervalo abierto que
contiene a c.
2. Si f''( c ) > 0, entonces f tiene un mínimo relativo en (c, f ( c )). En la figura 7 el punto C
cumple con esta condición.
3. Si f''( c ) < 0, entonces f tiene un máximo relativo en (c, f ( c )). En la figura 7 el punto A y el
punto E cumple con esta condición.
Si f''( c ) = 0, entonces el criterio falla. Esto es, f posiblemente tiene un máximo relativo, un mínimo
relativo o ninguno de los dos. En este caso, se puede utilizar el criterio de la primera derivada.
1.4.3. Punto de inflexión
Si (c, f ( c )) es un punto de inflexión de la gráfica de f, entonces f''( c ) = 0 o f '' no existe en x = c.
En la figura 7 el punto B y el punto D cumplen con esta condición.
Si f''( x ) cambia de signo cuando pasa por x = c, hay un punto de inflexión en x = c.
POLITÉCNICO GRANCOLOMBIANO
12
Ejemplo 4
Analicemos la propagación de una epidemia que tiene un comportamiento descrito en la siguiente
función:
n = f ( t ) = -0.3t³ + 10t² + 300t + 250
Donde n representa el número de personas afectadas por la epidemia y t representa el número de
días desde la detección inicial de la epidemia hasta un día posterior. Determinar:
1. Puntos críticos
Igualemos f'( x ) = 0
f'( t ) = -0.9t² + 20t + 300
-0.9t2 + 20t + 300 = 0
Los valores para los cuales la anterior expresión matemática se iguala a cero es:
Estos valores se obtienen resolviendo la fórmula general de la ecuación cuadrática.
Aproximadamente obtenemos los siguientes valores:
t1 = -10.2615
y
t2 = 32.4838
De estos dos valores obtenidos tienen sentido aquellos valores de t > 0, pero para nuestro análisis
tendremos todos los valores de t.
2. Intervalos de crecimiento, máximos y mínimos relativos
Luego de obtener los valores críticos para cuando t = -10.2615 y t = 32.4838, con este resultado
podemos dividir la recta real en los intervalos (-∞, -10.26),(-10.26,32.48) y (32.48, +∞),
tal como se muestra en la figura 8.
Notamos un decrecimiento en la función en los intervalos (-∞, -10.26) y (32.48, + ∞) y un
crecimiento en (-10.26,32.48).
POLITÉCNICO GRANCOLOMBIANO
13
Por otro lado, tenemos un mínimo relativo cuando pasamos del intervalo de (-∞,-10.26)
a (-10.26,32.48); es decir, vamos de un intervalo donde la función es decreciente a otro
donde es creciente. También encontramos un máximo relativo cuando pasamos del intervalo
(-10.26,32.48) a (32.48, + ∞), lo que significa que vamos de un intervalo donde la función
es creciente a otro donde es decreciente.
3. Punto(s) de inflexión
Para los puntos de inflexión encontremos los puntos donde f''( x ) = 0
f''( t )= -1.8t + 20 = 0
Es decir que para t = 11.11 hay un cambio de concavidad, tal como vemos en la figura 8.
Interpretación. El punto de inflexión puede interpretarse como la representación del punto en el
tiempo cuando decrece la tasa a la que se contagian las personas con gripe.
Antes de t = 11.11 se contagian personas adicionales con una tasa creciente.
Después de t = 11.11 se contagian personas adicionales, pero con una tasa decreciente.
¿Sabía que...?
Al obtener la gráfica de la derivada de una función es
importante deducir cuál debe ser la concavidad de la curva;
en este caso, lo determinamos intuitivamente. Siempre
existen solo dos posibilidades: que sea cóncava hacia arriba
o hacia abajo. Hay que poner especial atención en que no
se alteren las características que determinamos y que se
incluyan en la gráfica de la función derivada.
POLITÉCNICO GRANCOLOMBIANO
14
4. Intervalos de concavidad
Para ello hacemos uso de la relación entre la segunda derivada y la concavidad, y tenemos presente el
punto de inflexión encontrado. Luego realizamos una división de nuestra recta real en dos intervalos
(-∞, 11.11) y (11.11, + ∞), y con unos valores de prueba arbitrarios es posible saber el signo que
tiene en estos tramos (ver figura 8).
Figura 8. Descripción de la propagación de una epidemia
Fuente: elaboración propia
En síntesis...
»»
La primera derivada se usa para determinar los puntos críticos y los
intervalos donde la función es creciente y decreciente.
»»
La segunda derivada se usa para determinar la concavidad y los puntos de
inflexión.
POLITÉCNICO GRANCOLOMBIANO
15
Referencias
Tan, S. (2010). Matemáticas aplicadas a los negocios, las ciencias sociales y la vida (5ª ed.). Mexico:
Cengage Learning.
POLITÉCNICO GRANCOLOMBIANO
16
INFORMACIÓN TÉCNICA
Módulo: Matemáticas II
Unidad 3: Puntos críticos y óptimos
Escenario 5: Trazado de curvas con la ayuda de la derivada
Autor: Rogelio Alvarado Martínez
Asesor Pedagógico: Jeiner Velandia Sanabria
Diseñador Gráfico: Daniel Moreno Sarmiento
Asistente: Ginna Quiroga
Este material pertenece al Politécnico Grancolombiano.
Prohibida su reproducción total o parcial.
POLITÉCNICO GRANCOLOMBIANO
17