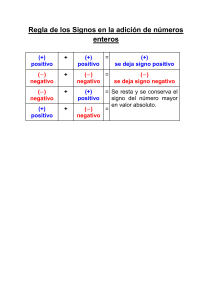
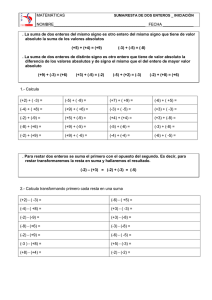
Guía de Apoyo al aprendizaje N°1: Adición de Números Enteros Adición de números enteros (Usando la Recta Numérica) Al sumar dos números enteros utilizando la recta numérica nos posicionaremos en el primer número, y avanzaremos hacia: - La derecha si el número es positivo. - La izquierda si el número es negativo. El número de espacios que se avanzará corresponde al valor absoluto del segundo número. Ejemplo 1: -2+3 Nos posicionamos en el primer número, que sería el (-2). El número 3 es positivo, por lo que avanzaremos hacia la derecha. Su valor absoluto es 3, por lo que nos moveremos tres espacios y llegaremos al número 1. Finalmente, podemos decir que: -2+3=1. Ejemplo 2: 4+(-8) Nos posicionamos en el primer número, que sería el 4. El número -8 es negativo, por lo que avanzaremos hacia la izquierda. Su valor absoluto es 8, por lo que nos moveremos ocho espacios y llegaremos al número -4. Finalmente, podemos decir que: 4+(-8)=-4. I. Resuelva las siguientes sumas de números enteros utilizando la recta numérica: Reglas en la adición * Al sumar dos números del mismo signo: Se conserva el signo y se suman los valores absolutos de los números. Ejemplos: 3 + 4 = ¿? En ese caso, ambos números tienen el mismo signo, que es positivo. Conservaremos su signo (+) y realizamos la suma de los valores absolutos: |3|= 3 y |4|= 4. Entonces, 3 + 4 = 7. (-5) + (-2) = ¿? En ese caso, ambos números tienen los signos iguales, que es negativo. Conservaremos su signo (-) y realizamos la suma de los valores absolutos: |-5|= 5 y |-2|= 2. Entonces, 5 + 2 = 7. Se conserva el signo (-), por lo que el valor de la operación final será -7. * Al sumar dos signos con números diferentes: Se conserva el signo del número con mayor valor absoluto. Luego, de los valores absolutos al mayor se le resta el menor. Si ambos números tienen igual valor absoluto, y signos diferentes, su suma va a ser igual a cero. Ejemplos: (-3) + 4 = ¿? En ese caso, ambos números tienen distinto signo (uno es positivo y el otro es negativo). Conservaremos el signo (+) ya que el número 4 es más grande que el 3. Se calculan los valores absolutos: |-3|=3 y |4|=4. Se resta el mayor con el menor: 4 - 3= 1. Como el signo que conservamos fue el (+) entonces el valor de la operación final será +1 = 1. (5) + (-8) = ¿? En ese caso, ambos números tienen distinto signo (uno es positivo y el otro es negativo). Conservaremos el signo (-) ya que el número 8 es más grande que el 5. Se calculan los valores absolutos: |5|=5 y |-8|=8. Se resta el mayor con el menor: 8 - 5= 3. Como el signo que conservamos fue el (-) entonces el valor final será -3. AYUDA: Observa la siguiente tabla que resume los resultados de la suma de los números enteros más pequeños: I. Resuelva las siguientes sumas: a) 8 + 20 = b) (-15) + (-3) = c) 17 + (-19) = d) (-6) + 20 = e) (-11) + 4 = f) 18 + (-17) = g) (-7) + (-10) = h) 10 + 2 = i) 4 + (-16) = j) (-1) + (-16) = k) (-8) + 16 = l) 12 + (-14) = m) (-18) + (-5) = n) (-20) + 11 = ñ) 13 + (-9) = II. Resuelva en su cuaderno las siguientes sumas de más de dos números enteros. Puede ir agrupando de dos números e ir resolviendo o junte según su signo, es decir, positivos con positivos y negativos con negativos para resolver: III. Cuadrados de adición. Se completan los espacios vacíos sumando de la siguiente manera, observa el ejemplo: + -1 4 Complete los siguientes cuadrados: -5 (-1)+(-5)=-6 4+(-5)=-1 7 -1+(7)=6 4+7=11