Centro-de-Gravedad-Ejercicios-Resueltos

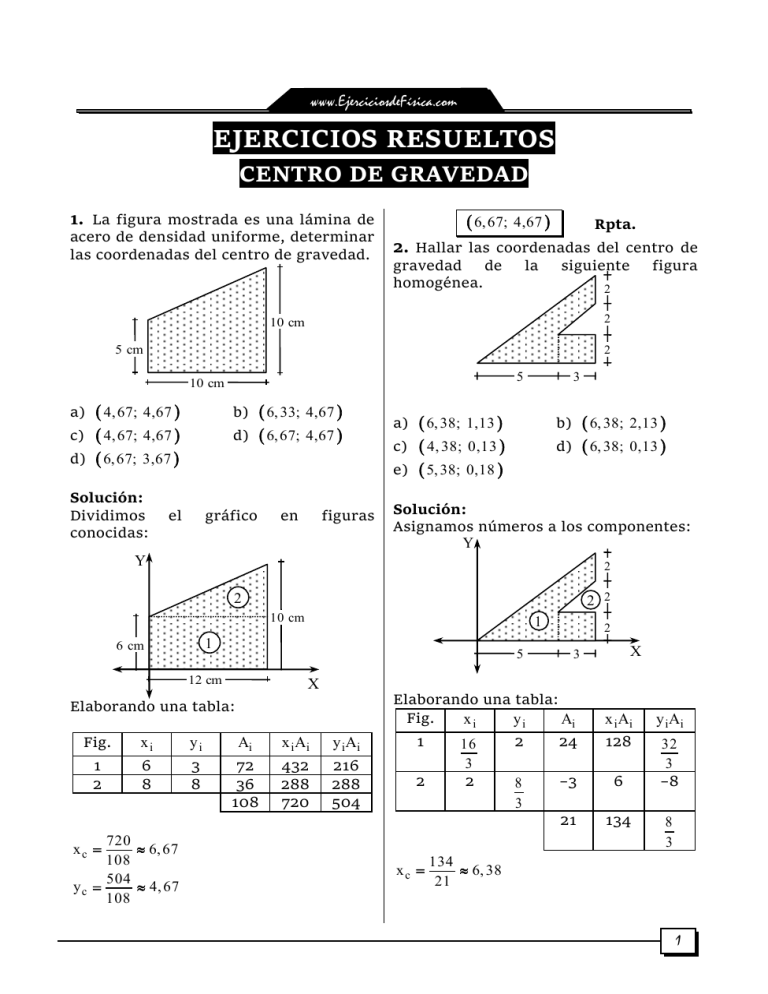
www.EjerciciosdeFísica.com
EJERCICIOS RESUELTOS
CENTRO DE GRAVEDAD
 6, 67; 4,67 
1. La figura mostrada es una lámina de
acero de densidad uniforme, determinar
las coordenadas del centro de gravedad.
Rpta.
2. Hallar las coordenadas del centro de
gravedad
de
homogénea.
la
siguiente
2
2
10 cm
5 cm
2
5
10 cm
 4, 67; 4,67 
 4, 67; 4,67 
d)  6, 67; 3,67 
a)
b)
c)
d)
Solución:
Dividimos
conocidas:
figura
el
 6, 33; 4,67 
 6, 67; 4,67 
gráfico
en
figuras
3
 6, 38; 1,13 
c)  4, 38; 0,13 
e)  5, 38; 0,18 
 6, 38; 2,13 
d)  6, 38; 0,13 
a)
b)
Solución:
Asignamos números a los componentes:
Y
Y
2
2 2
2
10 cm
1
1
6 cm
5
12 cm
X
3
X
Elaborando una tabla:
Fig.
xi
yi
Ai
x i Ai
y i Ai
1
2
6
8
3
8
72
36
108
432
288
720
216
288
504
720
xc 
 6, 67
108
504
yc 
 4, 67
108
2
Elaborando una tabla:
Fig.
xi
yi
Ai
1
2
24
16
3
2
2
–3
8
3
21
xc 
x i Ai
128
6
134
y i Ai
32
3
–8
8
3
134
 6, 38
21
1
www.EjerciciosdeFísica.com
x c  yc  5
8
y c  3  0,13
21
 6, 38; 0,13 
Rpta.
Rpta.
3. Hallar la suma de las coordenadas
del centro de gravedad de la varilla
doblada en U, que se muestra en la
figura:
5 cm
5 cm
a) 4
d) 6
b) 5
e) 4, 8
c) 4, 5
Solución:
Y
5 cm
1
4. Una varilla de 20 cm de largo se
dobla en dos partes iguales formando un
ángulo de 60°. ¿A qué distancia del
vértice “O” se encuentra el centro de
gravedad de la varilla doblada?
7
a)
3
2
O
5
b)
3
3
60º
3
c)
3
2
7
d)
3
8
5
e)
3
2
Solución:
Ubicamos de manera conveniente en un
eje de coordenadas:
Y
1
3
5
5
2
2
Elaborando una tabla:
Fig.
xi
yi
Li
1
2
3
0
2,5
5
2,5
0
2,5
37, 5 375 5


15
150 2
37, 5 375 5
yc 


15
150 2
xc 
2
5
5
5
15
(x c , y c )
X
5 cm
5
2
x iLi
y iLi
0
12,5
25
37,5
12,5
0
12,5
37,5
3
O
5
30º
d
2
10 cm
Construimos nuestra tabla:
Fig.
xi
yi
Li
5
5
3
1
10
3
2
2
5
0
10
20
75 15
xc 

Luego:
20
4
X
x iLi
y iLi
25
25 3
50
75
25 3
0
www.EjerciciosdeFísica.com
25
20
yc 
3
5
4
Elaboremos la tabla de valores:
3
Por Pitágoras:
C.G.
1
d
yc
2
 15 
5

2
d 
3
 
 4 
4

225
75
300
d2 


16 16
16
3
2
5
2
d
3
Rpta.
placa mostrada.
y i Ai
0
4a
3
 2
a
2
0
2 3
a
3
a
2
2a
3
 2
 a
8
a
16
2a
3
 2
 a
8

a
2
Luego:
1 3
a
yc  2
 2
a
4
3a
2
3a
e)

b)
c)
2a

b) 145 m

3

a
12
a
16

a
12
0
1 3
a
2
3
3
Rpta.
O
154 m
e) 125 m
B
Solución:
A
154 m
(x 3 , y 3 )
1
(x1, y1 )
O
3
4a
3
2a
60º
c) 147 m
d) 152 m
Solución:
Dividimos la placa en formas conocidas
(semicírculos).
(x c , y c )
Y
2
2a

 yc 
3
carril de vía férrea curvada según se
muestra en la figura. Si se sabe que el
radio de curvatura es igual a 154 m.
A
22
Considere:  
.
7
154 m
a) 150 m
a
2
(x 2 , y 2 )
x i Ai
6. Determinar la posición del C.G. de un
a
2
2a
3
5a
d)
4
Ai
 2
a
4
5. Hallar la coordenada yC del C.G. de la
a)
yi
xc
2
O
xi
4a
3
30º
G
154 m
X
Rsen 
OG 

B
3
www.EjerciciosdeFísica.com
OG 
154 sen

6

6
1
154( )
2  6(7)(77)
OG 
1 22
22
( )
6 7
OG  147 m
Rpta.
7. Hallar el centro de gravedad del
alambre, en función de “R”, con
respecto al sistema de coordenadas que
se indica.
Y
1
R
2R

R
R
2
3R
2
R

R
2
3 R
4
3
R
2
R
2
R
4
2 R
2R

R

xc 
X
R
2
2
2
R2
2
2

2
2
R
2
2R
2
2
2 R
R
2 R
2
2R
R

2 R 
Finalmente:
yc 
1



R
2
2R
De donde:

C.G.  R  1,
R
2
Rpta.
8. Determinar la posición del centro de
gravedad de la placa que se muestra:
20 cm
1 

a) R  1,

 2 
 1
R  1, 
 
2

d) R  1,



1

b) R  2,



c)
5 cm
12 cm
22 cm
4 

e) R  1,

3 

8 cm
Solución:
14 cm
Y
1
R
O
R/2
a) (7,58; 10,48)
c) (7,25; 11,06)
e) (7,31; 11,61)
2
2R

2r

b) (7,50; 11,53)
d) (6,34; 10,65)
R/2
2r

X
3
Completamos nuestra tabla:
xi
yi
Li
x iLi
Solución:
Dividimos
conocidas:
la
figura
en
Y
y iLi
20 cm
5 cm
4
12 cm
22 cm
formas
www.EjerciciosdeFísica.com
C.G.  (x c , y c )  (0, 0)
Y
Cálculo de Volúmenes:
Vcono 
Vesfera
1
2
3
yi
Ai
10
4
7
19,5
12,5
4
100
72
112
284
2072
 7, 30
284
Finalmente:
C.G.  (7, 31; 11, 61)
xc 
x i Ai
y i Ai
1000 1950
288
900
784
448
2072 3298
3298
yc 
 11, 61
284
4 R

3
h
4
R
b) 4R
R
c) 2R
R
e) 5R
Solución:
Sea el origen de coordenadas el centro
de gravedad (punto de contacto).
Vi
y iVi
2
R h
12
R h
3
h
4
3
2 2
4 R
4 R

3
3
La coordenada y c debe ser cero:
2
4
–R
2 2
4
R h
4 R

12
3 0
yc 
2
3
R h 4 R

3
3
R h
4 R

12
3
2
se ha colocado un cono cuya base
circular tiene su radio igual al de la
esfera. ¿Qué altura debe tener dicho
cono para que el C.G. del sistema se
encuentre en el punto de contacto?
a) 3R
X
3
yi
1
C.G.
h
2 2
Rpta.
9. Sobre una esfera maciza de radio “R”
d) R
R h
3
Fig.
Las áreas parciales son rectángulos, sus
centros
de
gravedad
son
las
intersecciones de sus diagonales.
xi
2
h
 4R 2
4
h  4R

4
2
h  16R
2
Rpta.
10.
Calcular el ángulo de equilibrio
para la plancha metálica semicircular
mostrada.
 2 
a) arc tan 

 3 
 4 
b) arc tan 

 3 

 5 
c) arc tan 

 3 
 4 
R
d) arc cot 

 3 
e) arc tan 2
5
www.EjerciciosdeFísica.com
Solución:
Por condición de equilibrio de un cuerpo
suspendido, la vertical que contiene la
cuerda debe pasar por su C.G. Además
de ubicarse sobre su eje de simetría.
4R
Se sabe que: y 
3
En el triángulo rectángulo:
4R
4
tan   3  
R
3
 4 

  arc tan 
 3 
Rpta.
x  12 cm
Rpta.
12.
Determinar la coordenada y c del
de gravedad de la figura.
R  4 cm .
R
a) 
4
R
b) 
5
2R
c) 
5
R
R
d) 
6
3R
e) 
8
centro
11. Un alambre rígido homogéneo de 25
cm de longitud es doblado como se
indica en la figura. ¿Cuánto debe medir
“x” para mantener O
equilibrio?
x
5 cm
Solución:
Ubicamos el origen de coordenadas en
el centro del círculo mayor (Eje de
simetría – eje Y).
Y
a) 10 cm
d) 12 cm
b) 15 cm
e) 16 cm
c) 10 cm
2
Solución:
D.C.L. de la barra
W2
x  10
B
5
O
(x c , y c )
C
20  x
10
R
A W1
x
Como el alambre es homogéneo, su peso
es proporcional a su longitud:
M0  0 :
W1(20  x)  W2 (x  10)  0
5k(20  x)  20k(x  10)
6
X
R
1
Elaborando el cuadro respectivo:
Fig.
yi
Ai
y i Ai
1
0
2
R
2
R
2
0
R 2
4

R 3
8
3
2
R
4

R 3
8

www.EjerciciosdeFísica.com
yc 

R 3
8
3
2
R
4

yc 
R

6
x
Rpta.
A1 x 1  A 2 x 2 900  15   36   24 

A1  A 2
900  36 
x  13,7 cm
 Ahora para la ordenada.
A y  A 2 y 2 900  15   36   10 
y 1 1

A1  A 2
900  36 
y  15,7 cm
 Entonces el centro de gravedad es:
C.G. = (13,7; 15,7)
13.
Encuentre las coordenadas del
C.G. de la placa metálica de espesor
uniforme. Considere π = 3,1.
Y(cm)
30 cm
30 cm
6 cm
10 cm
X(cm)
 Hallando las coordenadas del centro
de gravedad y las áreas respectivas.
Área
X
Y
900 cm2
15
15
36π cm2
24
10
Para la absisa
7