Document
Anuncio
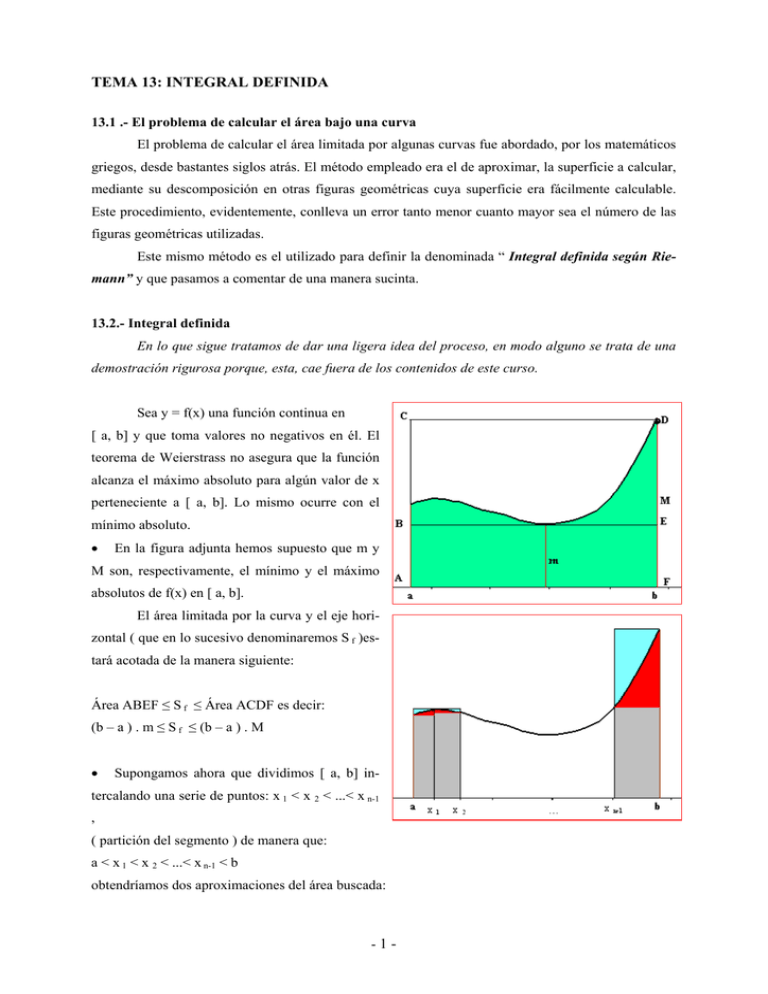
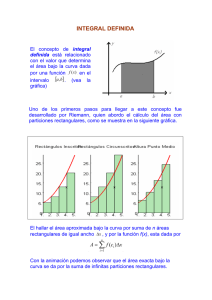
TEMA 13: INTEGRAL DEFINIDA 13.1 .- El problema de calcular el área bajo una curva El problema de calcular el área limitada por algunas curvas fue abordado, por los matemáticos griegos, desde bastantes siglos atrás. El método empleado era el de aproximar, la superficie a calcular, mediante su descomposición en otras figuras geométricas cuya superficie era fácilmente calculable. Este procedimiento, evidentemente, conlleva un error tanto menor cuanto mayor sea el número de las figuras geométricas utilizadas. Este mismo método es el utilizado para definir la denominada “ Integral definida según Riemann” y que pasamos a comentar de una manera sucinta. 13.2.- Integral definida En lo que sigue tratamos de dar una ligera idea del proceso, en modo alguno se trata de una demostración rigurosa porque, esta, cae fuera de los contenidos de este curso. Sea y = f(x) una función continua en [ a, b] y que toma valores no negativos en él. El teorema de Weierstrass no asegura que la función alcanza el máximo absoluto para algún valor de x perteneciente a [ a, b]. Lo mismo ocurre con el mínimo absoluto. • En la figura adjunta hemos supuesto que m y M son, respectivamente, el mínimo y el máximo absolutos de f(x) en [ a, b]. El área limitada por la curva y el eje horizontal ( que en lo sucesivo denominaremos S f )estará acotada de la manera siguiente: Área ABEF ≤ S f ≤ Área ACDF es decir: (b – a ) . m ≤ S f ≤ (b – a ) . M • Supongamos ahora que dividimos [ a, b] in- tercalando una serie de puntos: x 1 < x 2 < ...< x n-1 , ( partición del segmento ) de manera que: a < x 1 < x 2 < ...< x n-1 < b obtendríamos dos aproximaciones del área buscada: -1- - La primera ( rectángulos de color gris )formada por una serie de rectángulos de bases : x 1 – a, x 2 – x 1, . . . . . , b - x n-1 y alturas respectivas m 1, m 2 , ... , m n ( mínimos absolutos en cada uno de los interva- los obtenidos en la subdivisión El área encerrada por todos ellos será: s 1 = (x 1 – a) . m 1 + (x 2 – x 1 ) . m 2 + . . . . . + (b - x n-1 ) . m n - La segunda ( rectángulos de color azul )formada por una serie de rectángulos de las mismas bases que en el apartado anterior y alturas respectivas M 1, M 2 , ... , M n ( máximos absolutos en cada uno de los intervalos obtenidos en la subdivisión El área encerrada por todos ellos será: S 1 = (x 1 – a) . M 1 + (x 2 – x 1 ) . M 2 + . . . . . + + (b - x n-1 ) . M n Con las consideraciones realizadas hasta ahora tenemos que: (b – a) . m ≤ s 1 ≤ S 1 ≤ M ( b – a ) A medida que vayamos aumentando el número de puntos de la partición de [ a, b] ( ver figura adjunta) también aumentará el número de rectángulos obtenidos por el procedimiento señalado anteriormente. Para cada una de las particiones obtenidas iríamos obteniendo dos series de sumas que verificarían la relación: - Para las aproximaciones por defecto ( rectángulos rojos ) s 1 ≤ s 2 ≤ s 3 ≤. .... ≤ s n (1) - Para las aproximaciones por exceso ( rectángulos azules ) S 1 ≥ S 2 ≥ S 3 ≥. .... ≥ S n (2) En resumen tenemos que en cada etapa mejoraremos ( o al menos no empeora ) las aproximaciones del área limitada por la función f(x) Las sucesiones obtenidas en (1) y (2) forman un par de sucesiones monótonas convergentes porque: La sucesión (1) es monótona creciente La sucesión (2) es monótona decreciente Para una división de [a, b]cualquiera se verifica que s i ≤ S i La sucesión S 1 – s 1 , S 2 – s 2 , S 3 – s 3 , ...,Sn – s n es una sucesión cuyo límite es cero La consecuencia es que las dos sucesiones tienen el mismo límite. Este límite se define como integral definida de la función f (x) en el intervalo [a, b], y se representa en la forma donde f(x) es la función que describe la curva, a y b son los límites de integración; a es el límite inferior, y b, el límite superior. -2- 13.3 .- Propiedades de la Integral definida 1ª.- Si los límites de integración coinciden ∫ a f ( x).dx = 0 a 2ª.- Si f(x) > 0 y continua en [ a, b] entonces ∫ b 3ª.- Si f(x) < 0 y continua en [ a, b] entonces ∫ b a a f ( x).dx > 0 f ( x).dx < 0 4ª.- Si c es un punto interior del intervalo [ a, b], es decir, a < c < b y f(x) es continua [ a, b] entonces ∫ b a f ( x).dx = 5ª.6ª.- ∫ b ∫ b c a f ( x).dx + a a ∫ f ( x).dx + ∫ b a ∫ b c g ( x).dx = c. f ( x).dx = c. ∫ b a f ( x).dx ∫ b a ( f ( x) + g ( x) ).dx f ( x).dx cualquiera que sea c 7ª.- Si para todo x € [a, b] es f(x) ≤ g(x) entonces ∫ b a f ( x).dx ≤ ∫ b a g ( x).dx 8ª.- El valor de la integral definida cambia de signo si se permutan los límites de integración. 13.4 .- Teorema del valor medio de la integral Si f(x) es continua en un intervalo cerrado [a, b], existe un punto c en el interior del intervalo tal que: Al valor de f( c ) se le denomina valor medio de la función f(x) en el intervalo [a,b]. -3- Demostración Sea f(x) una función continua en [a,b]. Hemos dicho que el área encerrada por ella, el eje OX y las rectas x = a , x = b viene dada por: ∫ b a f ( x).dx Como f(x) es continua en [a,b] alcanzará el mínimo ( m ) y el máximo (M), absolutos, en algún punto del citado intervalo. ( En la figura adjunta, por sencillez, m lo alcanza en x = b y M en x = a ) Evidentemente Área rectángulo ABOP ≤ (b – a ) . m ≤ ∫ b a ∫ b a f ( x).dx ≤ área rectángulo ADRP es decir f ( x).dx ≤ ( b – a) . M Si dividimos a los tres miembros de la cadena de desigualdades por ( b – a ) resulta m ≤ 1 b−a ∫ b a f ( x).dx ≤ M Por el teorema de los valores intermedios ( Darboux), al ser f(x) continua en [a,b], alcanzará todos los valores intermedios entre m y M por lo que para algún x = c tendremos que 1 b−a ∫ b a f ( x).dx = f( c ) de donde tenemos finalmente que: ∫ b a f ( x).dx = ( b – a ) . f ( c ) es decir al área del rectángulo ACNP ( color rojo ) de la figura es idéntica a ∫ b a f ( x).dx NOTA Hasta ahora hemos indicado que representa ∫ b a f ( x).dx pero no hemos dicho cómo se calcula su va- lor. Esto lo haremos cuando hayamos visto la Regla de Barrow. Esta es la razón por la que ahora no proponemos ejemplos que aclaren este teorema 13.5 .- Teorema fundamental del cálculo integral Como hemos indicado anteriormente, hasta ahora, hemos dicho que si tenemos una función f(x), continua en [a,b], el área encerrada por ella, el eje OX y las rectas x = a , x = b viene dada por: -4- A= ∫ b a f ( x).dx Si consideramos ahora el intervalo [a, x] ⊂ [a,b] De igual manera podemos decir que F(X) = ∫ x a f (t ).dt representa el área de color, correspon- diente al intervalo [a, x], ( superficie marcada en rojo). Es evidente que esta superficie, F(x), dependerá de la posición que ocupe x en contraposición de A = ∫ b a f ( x).dx que será un número real. Con estas consideraciones el Teorema Fundamental del Cálculo Integral nos dice que: “ La función F(x) que nos describe el área limitada por la curva f(x), el eje de abscisas y las recta x = a y la abscisa variable x, es una función primitiva de la función f(x) “ F´(x) = f(x) El teorema fundamental del cálculo nos indica que la derivación y la integración son operaciones inversas. Al integrar una función continua y luego derivarla se recupera la función original. Ejemplos Calcula la derivada de las funciones siguientes 1.- F(x) = ∫ x 5 e t + 1 . dt En este caso f(t) = e t + 1 es una función continua. Por el T. Fundamental F´(x) = ex +1 -5- 2.- F(x) = ∫ x 4 + t 6 . dt 0 En este caso f(t) = 4 + t 6 es una función continua. Por el T. Fundamental F´(x) = 3.- F(x) = ∫ 3 sent . dt x Tenemos que F(x) = F´(x) = - 4 + x6 ∫ 3 sent . dt = - F(x) = - x ∫ x 3 sent . dt senx 4.- F(x) = ∫ x3 3 1 t 2 + 1 . dt Por ser el límite superior x 3 necesitamos realizar un cambio de variable u = x 3 Derivando según la regla de la cadena: dF ( x) dF ( x) d u = . dx du dx F´(x) = F(x) = x3 ∫ t 2 + 1 .dt = 3 1 5.- F(x) = ∫ x2 1 ∫ u 1 3 t 2 + 1 . dt. u du . = ( ∫ 3 t 2 + 1 ).dt. 3 x 2 = 1 dx 3 u2 +1 . 3 x 2 = 1 . dt 1+ t2 Por ser el límite superior x 3 necesitamos realizar un cambio de variable u = x 2 Derivando según la regla de la cadena: dF ( x) dF ( x) d u = . dx du dx F´(x) = F(x) = F´(x) = ∫ x2 1 u du 1 1 . dt = ( ∫ . dt) . 2 2 1 1+ t dx 1+ t 1 1 2x .2x = . 2x = 2 1+ u 1+ x4 1 + (x2 )2 6.- F(x) = ∫ senx 1 1 . dt 1− t2 Por ser el límite superior sen x necesitamos realizar un cambio de variable u = sen x Derivando según la regla de la cadena: -6- 3 x 6 + 1 .3 x 2 dF ( x) dF ( x) d u = . = F´(u).u´(x) dx du dx F´(x) = F(x) = ∫ senx 1 u du 1 1 . dt = ∫ . dt . 2 2 1 1− t dx 1− t 1 1 1 . cos x = . cos x = 2 2 cos x 1− t 1 − sen x F´(x) = 13.6 .- Regla de Barrow Nos dice que: si f(x) es continua en [ a, b], y G(x) es una de sus funciones primitivas, entonces: ∫ b a f ( x).dx = G(b) – G(a) lo cual quiere decir que, para hallar el área limitada por la curva, el eje de abscisas y las rectas x = a y x = b, comenzaremos buscando una primitiva cualquiera de f(x) y después hallaremos la diferencia de valores, G(b) – G(a), que toma dicha primitiva en los extremos del intervalo de integración. 13.7.- Fijando ideas Hasta ahora habíamos dicho que el área limitada por una curva, el eje de abscisas y las rectas x = a y x = b, la representábamos por ∫ b a f ( x).dx pero desconocíamos como encontrar su valor, sal- vo en algunos casos sencillos, porque no siempre era posible calcular el límite de la sucesión de sumas que obteníamos en la aproximación. El Teorema fundamental nos da una pista: “ la función que describe el área, F(x), es una primitiva de la curva que describe f(x)” pero aún así era necesario precisar más, de ahí la importancia de la Regla de Barrow que concreta, de manera precisa, cómo resolver el problema del área siempre y cuando seamos capaces de hallar G(x). Ejemplo-1 Calcular 1 1 ∫ 1+ x 0 2 . dx La función que describe la curva es f(x) = Una de sus funciones primitivas es G(x) = 1 1+ x2 1 ∫1+ x 2 dx = arc tg x El área buscada será pués G( 1 ) – G ( 0 ) = arc tg 1 – arc tg 0 = -7- π 4 Ejemplo 2 ( ejerc 63 pág 376 Ahora ya podemos proponer el siguiente ejemplo teorema del valor medio de la Integral definida Dada la función y = x 2, halla el punto c € [ 0, 2] tal que el área ∫ 2 0 x 2 dx sea igual a un rectángulo de base 2 y altura f(c ) Solución Área = ∫ 2 0 2 x3 8 x dx = = 3 0 3 2 Esta superficie equivale a un rectángulo 2 . f(c) de donde 2.f (c ) = 2 3 8 4 => f (c ) = = x 2 => x = 3 3 3 13.8.- Cálculo de áreas mediante integrales En la figura adjunta hemos representado el área encerrada por la función f(x) = x 3 – 2x2 – 6, el eje de abscisas y las rectas x = 1 y x = 4. La parte marcada con ( - ) es una superficie negativa mientras que la parte marcada con (+) es positiva. Si pretendiésemos calcular el área directamente hallando ∫ 4 1 ( x 3 − 2 x 2 − 6)dx cometeríamos un error porque al su- mar las dos partes, el total, se reduciría ya que estaríamos sumando dos cantidades de distinto signo. Para conseguir la solución correcta debes proceder en la forma: ∫ b • Supongamos que queremos hallar • Resuelves la ecuación f(x) = 0 para hallar los puntos de corte de la curva con el eje OX. Conside- a f ( x)dx remos, para fijar ideas, que las raíces son m < n. • Divides el intervalo de integración [a, b] en en la formas: [a, b] = [a, m] U [m, n] U [n, b] • Hallas una función primitiva G(x) de f(x) • Calculas las diferencias: |G(m) – G(a)|, | G(n) – G(m)| , | G(b) – G(n)| • Finalmente sumas los resultados obtenidos. -8- Ejemplos 1º.- Halla el área comprendida entre la función y = f(x) = x 3 – x 2 – 6x y el eje OX Solución Las raíces de f(x) son: - 2, 0 y 3 Primitiva de f(x) => G(x) = 3 2 ∫ ( x − x − 6 x) dx = x4 x3 - 3 x2 4 3 Cálculo de: G(- 2) = 4 + 8 − 16 - 12 = 3 3 G(0) = 0 G(3) = 81 − 63 - 9 – 27 = 4 4 Área = | G(0) – G(-2)| + |G(3) – G(0)| = |0 + 16 − 63 153 |+| - 0| = 3 4 12 A la derecha se muestra la representación gráfica del ejercicio 2º.- Calcula el área comprendida entre la curva f(x) = 3 x 2 – x + 1, el eje X y las rectas x = 0 y x=4 Solución Las raíces de f(x) son: No tiene Primitiva de f(x) = ∫ (3x 2 − x + 1) dx = x 3 - x2 +x 2 Cálculo de: G( 0 ) = 0 G( 4 ) = 64 – 8 + 4 = 60 Área = | 60 - 0| = 60 La superficie pedida aparece de color verde en la figura de la derecha 13.9.- Área comprendida entre dos curvas El área entre las gráficas de y=f(x) , y=g(x) en el intervalo [a,b] está dado por el valor de la Integral Definida de |f-g| en [a,b]. Consideraremos los casos siguientes: a) Que f(x) y g(x) no se cortan ( figura adjunta) -9- El área será la diferencia de las encerradas, por cada una de las curvas, el eje de abscisas y las rectas x = a y x = b ( superficie coloreada). A= ∫ b a f ( x)dx - ∫ b a g ( x)dx Que por las propiedades de la integral definida equivale a: A = ∫ b a ( f − g )( x) dx Es decir obtengamos la función diferencia ( f – g ) y obtengamos el área encerrada por esta curva entre los límites x = a, x = b y el eje de abscisas. Ejemplo Hallar el área encerrada por la curva y = x 2 – 2x + 1, la recta y = 1 y las rectas x = 3 y x = 5 ( superficie coloreada) Función f – g = (x 2 – 2x + 1) – ( 1 ) = x 2 – 2x A= 5 5 3 3 ∫ ( f − g )( x) dx = ∫ ( x 2 − 2 x) dx = x3 - x2 3 A(5) = 50 3 A(3) = 0 Área = 50 50 -0= 3 3 b) Que f(x) y g(x) se corten en dos puntos ⎧ y = f ( x) que equivale a encontrar las ⎩ y = g ( x) Para encontrar los puntos de corte se resuelve el sistema ⎨ soluciones de la ecuación f(x) – g(x) = 0 Las raíces de esta ecuación serán los límites de integración, procediendo, acto seguido, como en el apartado anterior. Ejemplo .- Halla el área limitada por la curva y = - x 2 + 3 x +4 y la recta y = 2x + 2 La función f(x) – g(x) = - x 2 + x +2 tiene como raíces x = - 1 y x = 2 el área pedida es pues ∫ 2 −1 ( f − g )( x)dx = ∫ 2 −1 (− x 2 + x + 2)dx - 10 - Una primitiva es A(x) = 2 ∫ (− x + x + 2)dx = - A(2) = - 8 10 +2+4= 3 3 A(- 1) = 1 1 7 + -2=3 2 6 Área A(2) – A( - 1) = x3 x2 + + 2x 3 2 27 6 c) Que f(x) y g(x) se corten en más de dos puntos En este caso, igual que en el apartado anterior, se buscan las raíces de la ecuación f(x) – g(x) = 0. Supongamos, para fijar ideas, que estas son m, n y p tales que: a<m<n<p<b Descomponemos el intervalo de integración [a, b] como unión de los subintervalos [a, m], [m, n], [n, p] y [p, b] para después calcular el área en cada uno de ellos y tomar el valor absoluto de la cantidad hallada. El área total será la suma de las áreas parciales encontradas. Ejemplo Ejercicio: 5-d) libro texto pág 373 ⎧ y = x( x − 1)( x − 2) ⎩y = 0 Calcula el área comprendida entre las curvas ⎨ Solución Las raíces de la función f(x) – g(x) = x ( x – 1) ( x – 2) – 0 = x ( x – 1) ( x – 2) son: x = 0, x = 1 y x = 2 El área pedida es A02 = | A02 | + | A02 | Buscamos una función primitiva, que será la misma para los dos sumandos. A(x) = ∫ x4 ( x – 3 x + 2 x) dx = - x3 + x2 4 3 2 A(0) = 0 A(1) = 1 4 A(2) = 0 A02 = | A02 | + | A02 | = | A(1) – A(0) | + | A(2) – A(1) | = - 11 - 1 1 1 +||= 4 4 2 La figura anterior es la representación gráfica del ejercicio. La función y = x ( x – 1) ( x – 2) está dibujada en color rojo mientras que y = 0 ( eje de abscisas) aparece en color negro 13.10.- Volumen de un cuerpo de revolución Supongamos que a la gráfica de f(x) se la hace girar alrededor del eje OX. La figura obtenida tiene un volumen que viene dado por: V= ∫ [ f ( x)] .π .dx b 2 a Ejemplo Se considera la circunferencia x 2 + y 2 = 25. Hallar el volumen de la esfera que se obtiene al girar alrededor de uno de sus diámetros dicha circunferencia. Solución La función de giro es: f(x) = 25 − x 2 Límites de integración: 25 – x 2 = 0 => x = -5 y x = 5 Volumen ∫ 5 −5 [ 25 − x ] .π .dx = ∫ 2 2 5 −5 π (25 − x 2 ).dx • Función primitiva V(x) = π ( 25x - • V(5) = 125 - • V(- 5) = - 125 + Volumen = π ( x3 ) 3 125 250 = 3 3 125 250 =3 3 250 250 500 -())=π 3 3 3 - 12 - Ejercicios 1º.- (ejerc 16 pág 373) Halla el área limitada por la función y = 2 x – x 2 y sus tangentes en los puntos en los que corta al eje de abscisas. Solución • Puntos de corte con el eje de abscisas 2 x – x 2 = 0 => x = 0 y x = 2 • Rectas tangentes y´= 2 – 2x => y´(0) = 2 e y´(2) = - 2 y = 2 x e y = - 2 ( x – 2 ) => y = - 2 x + 4 El área pedida aparece coloreada en la figura Necesitamos hallar la abscisa de intersección de ambas rectas tangentes ⎧ y = 2x => x = 1 ⎨ ⎩ y = −2 x + 4 Área azul Función diferencia (2 x – x 2 ) – 2x = - x 2 x3 1 => Área = A(1) – A(0) = Área = ∫ − x .dx = > A(x) = 0 3 3 1 2 Área amarilla Función diferencia (2 x – x 2 ) – ( - 2x + 4) = - x 2 + 4 x - 4 Área = ∫ 2 1 (− x 2 + 4 x − 4).dx = >A(x) = - Área total = x3 − 20 − 1 13 + 2 x – 4 x => Área = A(2) –A(1) = -( )= 3 3 3 3 1 13 14 + = 3 3 3 - 13 -