Teorema del límite central la distribución tiende

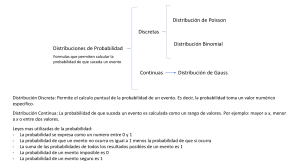
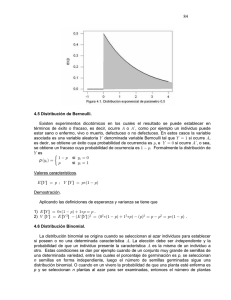
Teorema del límite central
El teorema del límite central o teorema central del límite indica que, en
condiciones muy generales, la distribución de la suma de variables aleatorias
tiende a una distribución normal (también llamada distribución gaussiana o
curva de Gauss o campana de Gauss) cuando la cantidad de variables es muy
grande.1
Teorema: Sea X1, X2,..., Xn una muestra aleatoria de una distribución con
media μ y varianza σ2. Entonces, si n es suficientemente grande, la variable
aleatoria
Tiene aproximadamente una distribución normal con
y
.
También se cumple que si
Tiene aproximadamente una distribución normal con
y
cuanto más grande sea el valor de n, mejor será la aproximación.
,
El teorema del límite central garantiza una distribución normal cuando n es
suficientemente grande.
Distribución binomial
En estadística, la distribución binomial es una probabilidad discreta que
mide el número de éxitos en una secuencia de n ensayos independientes
de Bernoulli con una probabilidad fija p de ocurrencia del éxito entre los
ensayos.
Un experimento de Bernoulli se caracteriza por ser dicotómico, esto es,
sólo son posibles dos resultados. A uno de estos se denomina éxito y tiene una
probabilidad de ocurrencia p y al otro, fracaso, con una probabilidad q = 1 - p.
En la distribución binomial el anterior experimento se repite n veces, de forma
independiente, y se trata de calcular la probabilidad de un determinado número
de éxitos. Para n = 1, la binomial se convierte, de hecho, en una distribución de
Bernoulli.
Para representar que una variable aleatoria X sigue una distribución binomial
de parámetros n y p, se escribe:
𝑥~𝐵(𝑛, 𝑝)
La distribución binomial es la base del test binomial de significación estadística
Distribución poisson.
En teoría de probabilidad y estadística, la distribución de Poisson es una
distribución de probabilidad discreta. Expresa la probabilidad de un número k
de eventos ocurriendo en un tiempo fijo si estos eventos ocurren con una
frecuencia media conocida y son independientes del tiempo discurrido desde el
último evento.
Nota: se utiliza cuando hay fenómenos que ocurren por razones o tasa
Un fenómeno es poisson cuando la tasa o razón no cambia ósea esta se
mantiene.
La función de masa de la distribución de Poisson es:
Pasos a utilizar en estadgraphics para distribuciones de probabilidad.
Gráficos
Distribución de probabilidad
selección de la probabilidad solicitada.
Descripción
Distribución
Distribución de probabilidad.
Graf. De probabilidad
Ajustes de distribución