INT 2 PG Ch 9_Spanish - CPM Educational Program

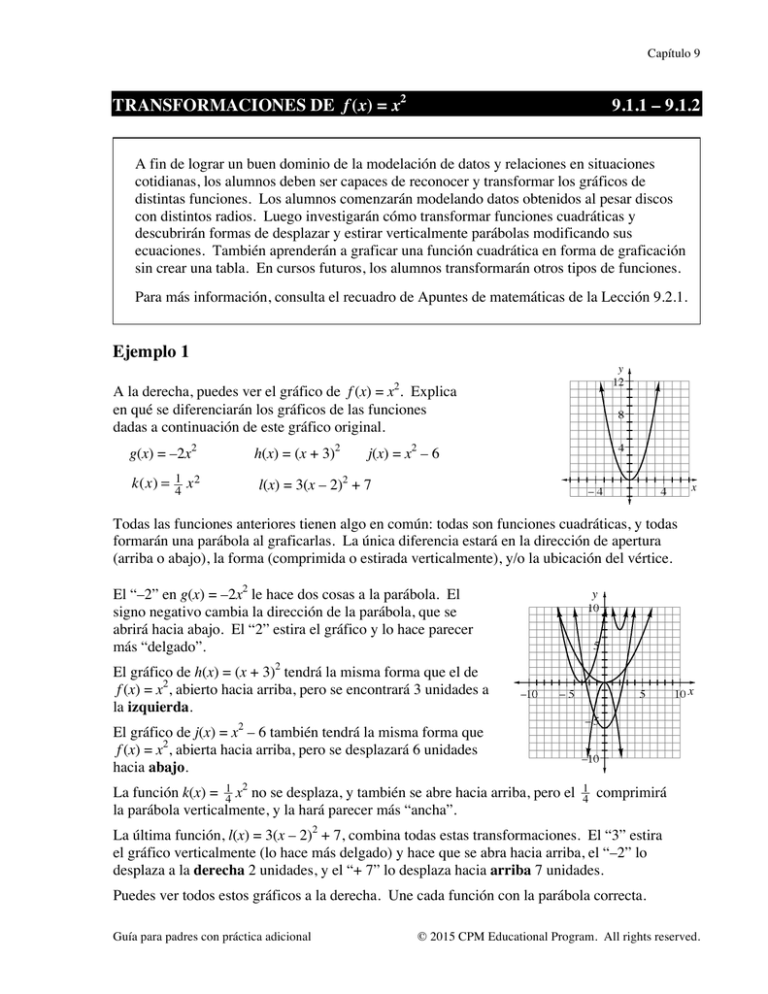
Capítulo 9
TRANSFORMACIONES DE f (x) = x2
9.1.1 – 9.1.2
A fin de lograr un buen dominio de la modelación de datos y relaciones en situaciones
cotidianas, los alumnos deben ser capaces de reconocer y transformar los gráficos de
distintas funciones. Los alumnos comenzarán modelando datos obtenidos al pesar discos
con distintos radios. Luego investigarán cómo transformar funciones cuadráticas y
descubrirán formas de desplazar y estirar verticalmente parábolas modificando sus
ecuaciones. También aprenderán a graficar una función cuadrática en forma de graficación
sin crear una tabla. En cursos futuros, los alumnos transformarán otros tipos de funciones.
Para más información, consulta el recuadro de Apuntes de matemáticas de la Lección 9.2.1.
Ejemplo 1
y
2
A la derecha, puedes ver el gráfico de f (x) = x . Explica
en qué se diferenciarán los gráficos de las funciones
dadas a continuación de este gráfico original.
g(x) = –2x2
h(x) = (x + 3)2
j(x) = x2 – 6
k(x) = 41 x 2
l(x) = 3(x – 2)2 + 7
x
Todas las funciones anteriores tienen algo en común: todas son funciones cuadráticas, y todas
formarán una parábola al graficarlas. La única diferencia estará en la dirección de apertura
(arriba o abajo), la forma (comprimida o estirada verticalmente), y/o la ubicación del vértice.
El “–2” en g(x) = –2x2 le hace dos cosas a la parábola. El
signo negativo cambia la dirección de la parábola, que se
abrirá hacia abajo. El “2” estira el gráfico y lo hace parecer
más “delgado”.
y
El gráfico de h(x) = (x + 3)2 tendrá la misma forma que el de
f (x) = x2, abierto hacia arriba, pero se encontrará 3 unidades a
la izquierda.
x
El gráfico de j(x) = x2 – 6 también tendrá la misma forma que
f (x) = x2, abierta hacia arriba, pero se desplazará 6 unidades
hacia abajo.
La función k(x) = 14 x2 no se desplaza, y también se abre hacia arriba, pero el
la parábola verticalmente, y la hará parecer más “ancha”.
1
4
comprimirá
La última función, l(x) = 3(x – 2)2 + 7, combina todas estas transformaciones. El “3” estira
el gráfico verticalmente (lo hace más delgado) y hace que se abra hacia arriba, el “–2” lo
desplaza a la derecha 2 unidades, y el “+ 7” lo desplaza hacia arriba 7 unidades.
Puedes ver todos estos gráficos a la derecha. Une cada función con la parábola correcta.
Guía para padres con práctica adicional
© 2015 CPM Educational Program. All rights reserved.
Ejemplo 2
¿Cuál es el vértice de la parábola de cada una de las funciones cuadráticas dadas a continuación?
f (x) = –2(x + 4)2 + 7
g(x) = 5(x – 8)2
h(x) =
3 2
5 x
–
2
5
En una función cuadrática, el vértice es el punto de ubicación. Nos da un punto de partida para
graficar la parábola rápidamente. El vértice de la función cuadrática en forma de graficación,
f (x) = a(x – h)2 + k, es el punto (h, k).
En la función f(x) = –2(x + 4)2 + 7, h = –4 y k = 7, así que el vértice es (–4, 7).
Ya que g(x) = 5(x – 8)2 también puede escribirse como g(x) = 5(x – 8)2 + 0, el vértice es (8, 0).
Reescribe h(x) =
3 2
5 x
–
2
5
como h(x) =
3
5
(x – 0)2 –
2
5
y podrás ver que su vértice es (0, – 25 ).
Problemas
Describe la transformación, grafica y halla el vértice de las siguientes funciones cuadráticas:
1.
y = –2(x – 1)2 + 3
2.
y = (x + 5)2 – 6
3.
y = (x + 2)2 – 25
4.
y = 2(x + 6)2 – 1
2.
Vértice: (–5, –6)
Respuestas
1.
Vértice: (1, 3)
y
Parábola abierta hacia
abajo, estirada
verticalmente, con su
vértice desplazado 1
unidad a la derecha y 3
unidades hacia arriba.
3.
Vértice: (–2, –25)
Parábola con su vértice
desplazado 5 unidades
a la izquierda y 6
unidades hacia abajo.
x
4.
y
Parábola con su vértice
desplazado 2 unidades
a la izquierda y 25
unidades hacia abajo.
© 2015 CPM Educational Program. All rights reserved.
x
y
Vértice: (–6, –1)
Parábola estirada
verticalmente, con su
vértice desplazado 6
unidades a la izquierda
y 1 unidad hacia abajo.
x
y
x
Core Connections en español, Matemática Integrada II
Capítulo 9
FORMA DE GRAFICACIÓN Y COMPLETAR CUADRADOS
9.1.3
En la Lección 9.1.3, los alumnos aprenderán que, cuando la ecuación de una parábola
está escrita en forma de graficación, f (x) = (x – h)2 + k, su vértice puede ser
identificado como (h, k). Por ejemplo, en el gráfico de f (x) = (x + 3)2 – 1, el vértice de la
parábola se encuentra en (–3, –1).
Cuando la ecuación de la parábola se encuentra en forma estándar, f (x) = ax2 + bx + c,
podemos usar el proceso de completar cuadrados para reescribir la ecuación en forma
de graficación. Podemos usar azulejos algebraicos para visualizar el proceso. Para
revisar este proceso, consulta la sección Resolver completando el cuadrado del
Capítulo 5 de esta Guía para padres con práctica adicional.
Ejemplo 1
Completa cuadrados para reescribir f (x) = x2 + 5x + 2 en forma de graficación. Identifica el
vértice y el punto de corte con el eje y, y grafica la parábola.
Mueve el término constante al otro lado de la ecuación: f (x) – 2 = x2 + 5x
Identifica el valor que debes sumar a ambos lados de la ecuación para convertir x2 + 5x en un
cuadrado perfecto, elevando al cuadrado la mitad del coeficiente término x:
Suma
25
4
( 52 )2 = 254
2
25
a ambos lados de la ecuación: f (x) − 2 + 25
4 = x + 5x + 4
(
5
Simplifica el lado izquierdo y factoriza el trinomio del lado derecho: f (x) + 17
4 = x+ 2
(
Esto puede reescribirse como: f (x) = x + 52
)2 − 174 .
(
)2
)
Ahora la función se encuentra en forma de graficación. El vértice es − 52 , − 17
4 o (–2.5, –4.25).
El punto de corte con el eje y es el punto donde x = 0.
y
Substituye x por 0 en la ecuación original: f (0) = 02 + 5(0) + 2 = 2;
el punto de corte con el eje y es (0, 2).
x
Usa el vértice y el punto de corte con el eje y para graficar la función.
Guía para padres con práctica adicional
© 2015 CPM Educational Program. All rights reserved.
Ejemplo 2
Completa cuadrados para reescribir f (x) = x2 + 8x + 15 en forma de graficación e identifica el
vértice de la parábola.
f (x) = x2 + 8x + 15
f (x) – 15 = x2 + 8x
Mueve el término constante al otro lado.
Suma el cuadrado de la mitad del
( )2
2
f (x) – 15 + 16 = x + 8x + 16
término x a ambos lados.
f (x) + 1 = x2 + 8x + 16
Simplifica el lado izquierdo de la ecuación.
2
f (x) + 1 = (x + 4)
Factoriza el lado derecho de la ecuación.
2
f (x) = (x + 4) – 1
Mueve el término constante de vuelta al lado derecho.
Por lo tanto, la ecuación en forma de graficación es f (x) = (x + 4)2 – 1. El vértice se encuentra
en (h, k) = (–4, –1).
Problemas
Completa cuadrados para reescribir la ecuación de cada función en forma de graficación.
Luego menciona el vértice de cada parábola.
1.
f (x) = x2 + 6x + 7
2.
f (x) = x2 + 4x + 11
3.
f (x) = x2 + 10x
4.
f (x) = x2 + 7x + 2
5.
f (x) = x2 – 6x + 9
6.
f (x) = x2 + 3
7.
f (x) = x2 – 4x
8.
f (x) = x2 + 2x – 3
9.
f (x) = x2 + 5x + 1
10.
f (x) = x 2 − 13 x
Respuestas
1.
f (x) = (x + 3)2 – 2; (–3, –2)
2.
f (x) = (x + 2)2 + 7; (–2, 7)
3.
f (x) = (x + 5)2 – 25; (–5, –25)
4.
f (x) = (x + 3.5)2 – 10.25; (–3.5, –10.25)
5.
f (x) = (x – 3)2; (3, 0)
6.
f (x) = x2 + 3; (0, 3)
7.
f (x) = (x – 2)2 – 4; (2, –4)
8.
f (x) = (x + 1)2 – 4; (–1, –4)
9.
5
21
f (x) = (x + 52 )2 − 21
4 ; (− 2 , − 4 )
10.
1 ; (1 , −
f (x) = (x − 16 )2 − 36
6
© 2015 CPM Educational Program. All rights reserved.
1
36 )
Core Connections en español, Matemática Integrada II
Capítulo 9
RESOLUCIÓN DE DESIGUALDADES CUADRÁTICAS
9.2.1
Existen varios métodos para resolver desigualdades cuadráticas con una variable, pero
un método que funciona con muchos tipos de desigualdades consiste en transformar la
desigualdad en una ecuación, resolverla, y graficar las soluciones en una recta numérica.
Las soluciones a la ecuación, llamadas puntos frontera, dividen la recta numérica en
regiones. Al probar un número de cada región en la desigualdad original, podemos
determinar si los números en esa región son soluciones. Los puntos frontera pueden ser
parte de la solución (≥ o ≤) o no (> o <), dependiendo del signo de desigualdad.
Para más información, consulta el recuadro de Apuntes de matemáticas de la Lección 9.2.2.
Ejemplo 1 Resuelve: x2 – 3x –18 < 0
Ejemplo 2 Resuelve: m2 – 3 ≥ 1
Conviértela en una ecuación y resuelve.
x2 – 3x – 18 = 0
(x – 6)(x + 3) = 0
x = 6 o x = –3 (los puntos frontera)
Conviértela en una ecuación y resuelve.
m2 –3 = 1
m2 = 4
m = ±2 (el punto frontera)
x
Si probamos x = –4, 0, 7 en la desigualdad
original, x = –4 es falso, x = 0 es verdadero,
y x = 7 es falso.
x
Si probamos m = –3, 0, 3 en la desigualdad
original, m = –3 es verdadero, m = 0 es falso,
y m = 3 es verdadero.
x
falso
verdadero
verdadero
falso
La solución son todos los números mayores
a –3 y menores a 6, lo que se escribe como
–3 < x < 6.
falso
x
verdadero
La solución son todos los números menores
o iguales a –2 o todos los números mayores
o iguales a 2, lo que se escribe como
m ≤ –2 o m ≥ 2.
Problemas
Resuelve las siguientes desigualdades:
1.
x2 + 6x + 8 < 0
2.
y2 – 5y > 0
3.
y2 – 5y < 0
4.
x2 – 3x – 4 < 0
5.
–x2 – 9x – 14 < 0
6.
y2 ≤ 16
7.
3x2 + 7x – 6 ≥ 0
8.
x2 + 4x – 8 < 4
9.
y2 + 6y + 9 > 0
10.
x(7x – 26) ≤ 8
Guía para padres con práctica adicional
© 2015 CPM Educational Program. All rights reserved.
Respuestas
1.
–4 < x < –2
2.
y<0oy>5
3.
0<y<5
4.
–1 < x < 4
5.
x < –7 o x > –2
6.
–4 ≤ y ≤ 4
7.
x ≤ –3 o x ≥
8.
–6 < x < 2
9.
todos los números excepto –3
10.
– 27 ≤ x ≤ 4
2
3
RESOLUCIÓN DE SISTEMAS DE ECUACIONES
9.2.2
En esta lección los alumnos se concentrarán en qué significa una solución a un sistema de
ecuaciones, tanto algebraicamente como gráficamente. También aplicarán lo que saben
sobre la resolución de sistemas lineales para resolver sistemas con funciones cuadráticas.
Ejemplo 1
Usa los gráficos de la parábola y = x2 – 3x – 10 y la recta y = –2x + 2
a la derecha. La parábola y la recta se cruzan dos veces, generando dos
puntos de intersección: (–3, 8) y (4, –6).
También puedes hallar los puntos de corte resolviendo el sistema de
ecuaciones algebraicamente.
Para resolver el sistema de ecuaciones, usa el Método de igualación de
sistema de ecuaciones (de Core Connections en español, Matemática
Integrada I) o el de sustitución.
x2 – 3x – 10 = –2x + 2
Suma y/o resta términos semejantes en ambos lados de la ecuación para igualar uno de los lados
a cero, y luego factoriza usando la Propiedad de producto cero para calcular x (también puedes
usar la Fórmula cuadrática).
x2 – x – 12 = 0
(x – 4)(x + 3) = 0
x = 4 o x = –3
Substituir x = 4 en cualquier ecuación arroja y = –6, así que (4, –6) es una solución al sistema.
Substituir x = –3 en cualquier ecuación arroja y = 8, así que (–3, 8) es una solución al sistema.
© 2015 CPM Educational Program. All rights reserved.
Core Connections en español, Matemática Integrada II
Capítulo 9
Ejemplo 2
Resuelve el sistema de ecuaciones de la derecha sin graficarlo.
Explica qué te dice la solución sobre el gráfico del sistema.
y = –2(x – 2)2 + 35
y = –2x + 15
Ambas ecuaciones están escritas en forma “y =”, así que puedes resolverlas usando el método
de sustitución.
–2(x –2)2 + 35 = –2x + 15
–2(x –2)2 = –2x –20
–2(x2 – 4x + 4) = –2x – 20
–2x2 + 8x – 8 = –2x – 20
–2x2 + 10x + 12 = 0
x2 – 5x – 6 = 0
(x – 6)(x + 1) = 0
x=6ox=–1
Sustituye cada valor de x en cualquiera de las ecuaciones para hallar el valor correspondiente
de y. Puedes usar cualquiera de las ecuaciones. Aquí usaremos la más simple.
x = 6, y = –2x + 15
y = –2(6) + 15
y = –12 + 15
y=3
Solución: (6, 3)
x = –1, y = –2x + 15
y = –2(–1) + 15
y = 2 + 15
y = 17
Solución: (–1, 17)
Finalmente, debemos probar cada punto en ambas ecuaciones para verificar nuestro trabajo.
(6, 3):
y = –2(x – 2)2 + 35
3 = –2(6 –2)2 + 35
3 = –2(16) + 35 ✓
(–1, 17):
y = –2(x – 2)2 + 35
17= –2(–1 – 2)2 + 35
17 = –2(9) + 35 ✓
(6, 3): y = –2x + 15
3 = –2(6) + 15 ✓
(–1, 17): y = –2x + 15
17 = –2(–2) + 15 ✓
Al resolver estas dos ecuaciones con dos incógnitas hallamos dos soluciones, y ambas funcionan
en las ecuaciones originales. Esto significa que los gráficos de las ecuaciones, una parábola y
una recta, se intersecan en exactamente dos puntos distintos. Esta solución puede ser confirmada
graficando los gráficos correspondientes.
Guía para padres con práctica adicional
© 2015 CPM Educational Program. All rights reserved.
Problemas
Resuelve los sistemas de ecuaciones a continuación algebraicamente. ¿Qué te dicen las
soluciones sobre el gráfico del sistema?
1.
y = – 23 x + 7
4x + 6y = 42
2.
y = (x + 1)2 + 3
y = 2x + 4
3.
y = –3(x – 4)2 – 2
y = – 47 x + 4
4.
x+y=0
y = (x – 4)2 – 6
5.
y = x2 – 3x + 2
y = x2 + 3x
6.
y = x2 – 6x + 9
y = x2 – 9
7.
y = 3x2 – 15x + 23
y = –x2 + 5x – 1
8.
y = 12 x 2 − 2x − 2.5
y = –2x2 – 12x – 16
9.
y = 4x2 – 12x + 5
y = –12x2 + 36x – 31
10.
y = 0.25x2 + 2x + 4
y = –0.25x2 + 4
Respuestas
1.
Todos los números reales. Al graficarlas,
estas ecuaciones producen la misma recta.
2.
(0, 4); la parábola y la recta se
intersecan una sola vez.
3.
No tiene solución. La parábola y la recta
no se intersecan.
4.
(2, –2) and (5, –5); la recta y la
parábola se intersecan dos veces.
5.
( 13 , 1 19 ); las parábolas se intersecan
una sola vez.
6.
(3, 0); las parábolas se intersecan
una sola vez.
7.
(2, 5) y (3, 5); las parábolas se intersecan
dos veces.
8.
No tiene solución. Las parábolas no
se intersecan.
9.
(1.5, –4); las parábolas se intersecan
una sola vez.
10. (–4, 0) y (0, 4); las parábolas se
intersecan dos veces.
© 2015 CPM Educational Program. All rights reserved.
Core Connections en español, Matemática Integrada II
Capítulo 9
TASA DE CAMBIO PROMEDIO
9.3.1
En cursos de matemáticas anteriores, los alumnos aprendieron que las funciones lineales
tienen una tasa de cambio constante igual que se corresponde con la pendiente de una
recta. En la Lección 9.3.1, aprenderán a calcular la tasa de cambio promedio de una
función no lineal en un intervalo dado. La tasa de cambio promedio se calcula hallando
la pendiente entre dos puntos del gráfico de la función. Si la pendiente representa una
distancia por tiempo, la tasa de cambio promedio describe la velocidad promedio.
Para más información, consulta el recuadro de Apuntes de matemáticas de la Lección 9.3.2.
Ejemplo 1
Usa los datos en la tabla de la derecha que indican la posición de
un objeto en momentos dados, para calcular la tasa de cambio
promedio durante los siguientes periodos:
Tiempo (s) Altura (m)
0.0
0.0
1.0
120.6
2.0
176.8
2.5
181.0
3.0
169.2
4.0
97.6
a.
0.0 a 1.0 segundos
b.
1.0 a 2.0 segundos
c.
2.0 a 2.5 segundos
d.
2.5 a 3.0 segundos
e.
3.0 a 4.0 segundos
f.
¿En qué periodo se mueve más rápido el objeto? ¿En qué periodo se mueve más lento?
¿En qué momento cambia de dirección?
Calcula la pendiente entre los puntos correspondientes a cada intervalo dado. Por ejemplo, los
puntos para el periodo 0.0 a 1.0 segundos son (0.0, 0.0) y (1.0, 120.6). Recuerda incluir las
unidades adecuadas en las respuestas.
m
= 120.6
1.0 = 120.6 s
a.
120.6−0
1.0−0
b.
176.8−120.6
2.0−1.0
c.
181−176.8
2.5−2.0
= 8.4
d.
169.2−181
3.0−2.5
= −23.6 ms
e.
97.6−169.2
4.0−3.0
f.
=
56.2
1.0
= 56.2 ms
m
s
= −71.6 ms
El objeto se mueve más rápido entre 0 y 1 segundo. Se mueve más lento (al viajar hacia
arriba) entre 2.0 y 2.5 segundos. Cambia de dirección entre 2.5 y 3.0 segundos.
Observa que, cuando la altura del objeto disminuye (cuando desciende), la tasa de cambio
promedio (velocidad) es negativa.
Guía para padres con práctica adicional
© 2015 CPM Educational Program. All rights reserved.
y
Ejemplo 2
Usa el gráfico de la derecha para estimar la tasa de cambio
promedio del intervalo:
a.
x = –1 a x = 1
b.
x=2ax=3
c.
x=4ax=5
d.
x=6ax=7
e.
x=8ax=9
x
Determina los puntos correspondientes a cada intervalo y calcula la pendiente correspondiente.
a.
(–1, –5) y (1, 4)
4−(−5)
1−(−1)
b.
(2, 7) y (3, 9)
9−7
3−2
c.
(4, 10) y (5, 10)
10−10
5−4
d.
(6, 9) y (7, 7)
7−9
7−6
= −2
e.
(8, 4) y (9, 0)
0−4
9−8
= –4
= 4.5
=2
=0
Problemas
Tiempo
(min)
Calcula la tasa de cambio promedio para los periodos dados
usando los datos en la tabla de la derecha.
1.
0 a 5 minutos
2.
10 a 15 minutos
3.
15 a 20 minutos
4.
25 a 30 minutos
0
5
10
15
20
25
30
Distancia desde
la línea inicial
(metros)
0
67.5
110
127.5
120
87.5
30
5.
t=0at=1s
6.
t=3at=4s
7.
t=4at=5s
8.
t=8at=9s
9.
t = 10 a t = 11 s
© 2015 CPM Educational Program. All rights reserved.
Altura (pies)
Usa el gráfico de la derecha para estimar la tasa de cambio
promedio de los periodos dados.
Tiempo (segundos)
Core Connections en español, Matemática Integrada II
Capítulo 9
Respuestas
1.
13.5 m/min
2.
8.5 m/min
3.
–1.5 m/min
4.
–11.5 m/min
5.
≈ 5 pies/s
6.
≈ 2 pies/s
7.
≈ 1.5 pies/s
8.
≈ –2 pies/s
9.
≈ –4.5 pies/s
FUNCIONES INVERSAS
9.4.1
Los alumnos explorarán funciones inversas, es decir, ecuaciones que “deshacen” las
acciones de otras funciones.
Por ejemplo, la función f (x) = 3x + 1 realiza las siguientes operaciones sobre x: multiplica
por 3 y suma 1. La función inversa, llamada f –1(x), revierte las operaciones: resta 1 y
divide por 3. Por lo tanto, f −1 (x) = x−1
3 .
Ejemplo 1
Halla la inversa de cada función.
a.
h(x) =
x−6
3
b.
g(x) = 2(x + 4)
La función del punto (a) resta 6 al valor de entrada (x) y divide el resultado por 3. La función
inversa revierte el proceso. Por lo tanto, la función inversa debería multiplicar por 3 y luego
sumar 6. La función inversa es h–1(x) = 3x + 6.
Prueba un valor de entrada en la función original: Para x = 6, h(6) =
6−6
3
=0.
–1
Usa el valor de salida como valor de entrada de la inversa: Para x = 0, h (0) = 3(0) + 6 = 6.
La función inversa “deshace” la función original, lo que arroja el valor de entrada original: 6.
En el punto (b), la función g(x) suma 4 al valor de entrada y multiplica el resultado por 2. La
función inversa debe dividir primero por 2 y luego restar 4. Por lo tanto, g–1(x) = 2x – 4.
Para verificar este resultado, prueba un valor de entrada en la función original:
g(1) = 2(1 + 4) = 10.
Usa el valor de salida como valor de entrada de la función inversa: g–1(10) =
10
2
– 4 = 5 – 4 = 1.
La función inversa “deshace” la función original, lo que arroja el valor de entrada original: 1.
Guía para padres con práctica adicional
© 2015 CPM Educational Program. All rights reserved.
Problemas
Escribe la inversa de cada una de las siguientes funciones:
2.
f (x) = – 43 x + 6
5(x+2)
3
4.
f (x) = 2x + 6
3x+6
5
6.
g(x) =
7.
g(x) = 4(x + 1) – 3
8.
j(x) = 2(x + 2)
9.
h(x) = 3x – 4
10.
g(x) = 6x + 2
1.
f (x) = 8(x – 13)
3.
f (x) =
5.
f (x) =
x
5
Respuestas
1.
f –1(x) =
x
8
+ 13
2.
f –1(x) = −
4
3
3.
f –1(x) =
3
5
x−2
4.
f –1(x) =
x−3
5.
f –1(x) = =
5 x−6
3
6.
g–1(x) = 5x
7.
g–1(x) =
x+3 − 1
4
8.
j –1(x) =
1
2
x−2
9.
h–1(x) =
1
3
10.
g–1(x) =
1
6
x − 13
x + 43
© 2015 CPM Educational Program. All rights reserved.
1
2
x+8
Core Connections en español, Matemática Integrada II