r о rˆ θˆ r о rˆ θ θˆ

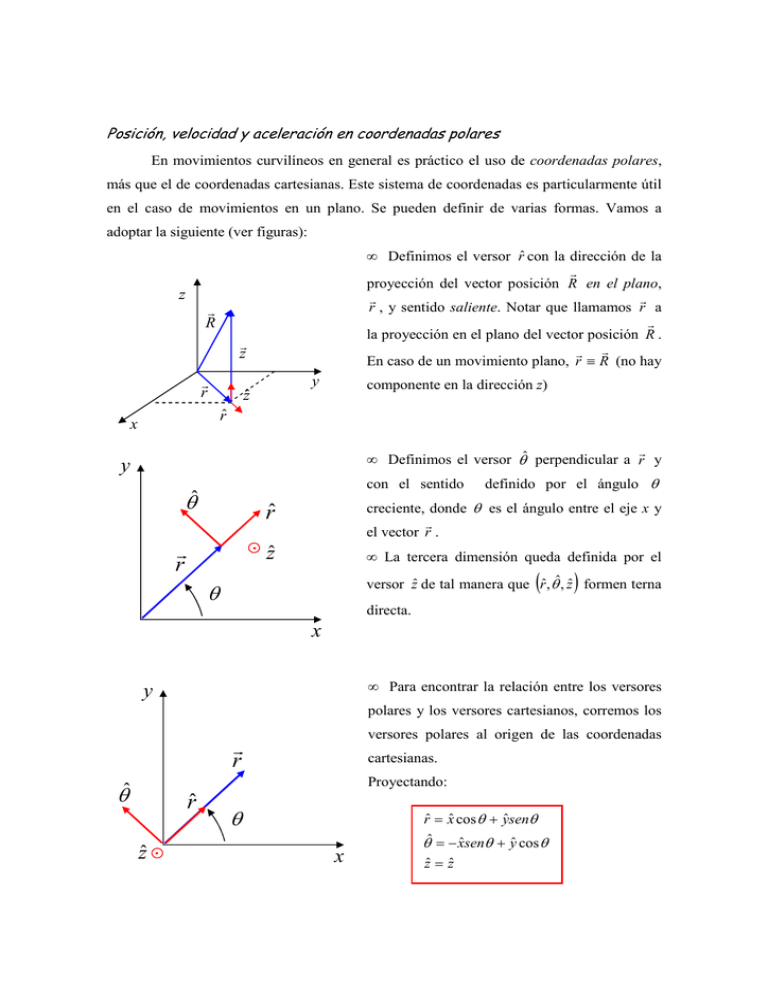
Posición, velocidad y aceleración en coordenadas polares
En movimientos curvilíneos en general es práctico el uso de coordenadas polares,
más que el de coordenadas cartesianas. Este sistema de coordenadas es particularmente útil
en el caso de movimientos en un plano. Se pueden definir de varias formas. Vamos a
adoptar la siguiente (ver figuras):
• Definimos el versor r̂ con la dirección de la
r
proyección del vector posición R en el plano,
r
r
r , y sentido saliente. Notar que llamamos r a
r
la proyección en el plano del vector posición R .
r r
En caso de un movimiento plano, r ≡ R (no hay
z
r
R
r
z
y
r
r
componente en la dirección z)
ẑ
r̂
x
r
• Definimos el versor θˆ perpendicular a r y
y
con el sentido
θˆ
r
r
definido por el ángulo θ
r̂
creciente, donde θ es el ángulo entre el eje x y
r
el vector r .
ẑ
• La tercera dimensión queda definida por el
(
)
versor ẑ de tal manera que rˆ, θˆ, zˆ formen terna
θ
directa.
x
• Para encontrar la relación entre los versores
y
polares y los versores cartesianos, corremos los
versores polares al origen de las coordenadas
r
r
cartesianas.
Proyectando:
θˆ
r̂
ẑ
θ
x
rˆ = xˆ cos θ + yˆsenθ
θˆ = − xˆsenθ + yˆ cos θ
zˆ = zˆ
De acuerdo con esta elección, el vector posición queda descrito en este sistema de
coordenadas:
r
R = rrˆ + zzˆ
r
r
Vamos a encontrar las expresiones de la velocidad v y la aceleración a en este sistema de
r
coordenadas, derivando la expresión de R . Notar que r̂ y θˆ , a diferencia de los versores
cartesianos, no son versores fijos, es decir, se mueven siguiendo el movimiento del vector
posición. Por lo tanto, dependen del tiempo y deben derivarse.
r
r dR d (rrˆ + zzˆ )
=
= r&rˆ + rr&ˆ + z&zˆ
v=
dt
dt
Tenemos que encontrar r&ˆ . Para ello, derivemos
las expresiones de los versores en
cartesianas:
r&ˆ = − xˆθ&senθ + yˆθ& cos θ = θ&(− xˆsenθ + yˆ cos θ = θ&θˆ
&
θˆ = − xˆθ& cos θ − yˆθ&senθ = −θ&( xˆ cos θ + yˆ senθ ) = −θ&rˆ
Entonces:
r
v = r&rˆ + rθ&θˆ + z&zˆ
La velocidad queda expresada como la suma de tres términos:
r
r&rˆ (velocidad radial), da cuenta del movimiento en la dirección radial ( r puede variar
en módulo).
r
rθ&θˆ (velocidad en θ ), da cuenta de los cambios de dirección de r
&z (velocidad en z), es idéntico a la componente de la velocidad en cartesianas. Este
zˆ
término es nulo si el movimiento es en un plano.
•
Vamos a encontrar la aceleración, como siempre, derivando la expresión de la
velocidad.
r
r dv
&
a=
= &r&rˆ + r&r&ˆ + r&θ&θˆ + rθ&&θˆ + rθ&θˆ + &z&zˆ
dt
Teniendo en cuenta las expresiones de las derivadas de los versores:
r
a = &r&rˆ + r&θ&θˆ + r&θ&θˆ + rθ&&θˆ − rθ& 2 rˆ + &z&zˆ
Agrupando los términos:
(
) (
)
r
a = &r& − rθ& 2 rˆ + 2r&θ& + rθ&& θˆ + &z&zˆ
En el caso que el movimiento sea en un plano, no hay componente en la dirección z, y
entonces resulta:
r
R = rrˆ
r
v = r&rˆ + rθ&θˆ
r
a = r&& − rθ& 2 rˆ + 2r&θ& + rθ&& θˆ
(
) (
)
-------------------------------------