Determinar la ecuación normal de una parábola

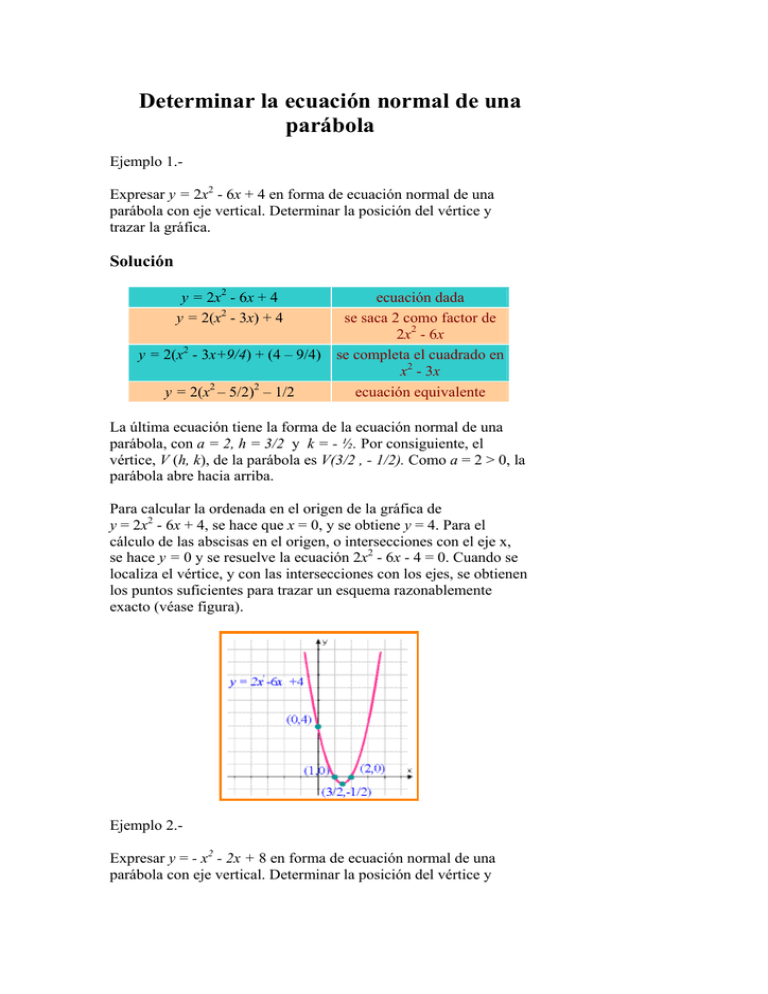
Determinar la ecuación normal de una
parábola
Ejemplo 1.Expresar y = 2x2 - 6x + 4 en forma de ecuación normal de una
parábola con eje vertical. Determinar la posición del vértice y
trazar la gráfica.
Solución
y = 2x2 - 6x + 4
y = 2(x2 - 3x) + 4
ecuación dada
se saca 2 como factor de
2x2 - 6x
y = 2(x2 - 3x+9/4) + (4 – 9/4) se completa el cuadrado en
x2 - 3x
y = 2(x2 – 5/2)2 – 1/2
ecuación equivalente
La última ecuación tiene la forma de la ecuación normal de una
parábola, con a = 2, h = 3/2 y k = - ½. Por consiguiente, el
vértice, V (h, k), de la parábola es V(3/2 , - 1/2). Como a = 2 > 0, la
parábola abre hacia arriba.
Para calcular la ordenada en el origen de la gráfica de
y = 2x2 - 6x + 4, se hace que x = 0, y se obtiene y = 4. Para el
cálculo de las abscisas en el origen, o intersecciones con el eje x,
se hace y = 0 y se resuelve la ecuación 2x2 - 6x - 4 = 0. Cuando se
localiza el vértice, y con las intersecciones con los ejes, se obtienen
los puntos suficientes para trazar un esquema razonablemente
exacto (véase figura).
Ejemplo 2.Expresar y = - x2 - 2x + 8 en forma de ecuación normal de una
parábola con eje vertical. Determinar la posición del vértice y
trazar la gráfica.
Solución
y = -x2 - 2x + 8
y =- (x2 + 2x) + 8
y =- (x2 + 2x + 1) + (8 + 1)
y =- (x – (- 1))2 + 9
y =- (x + 1)2 + 9
ecuación dada
se saca -1 como factor
común de -x2 -2x
se completa el cuadrado
en
2
x + 2x
ecuación equivalente
ecuación equivalente
Esta es la ecuación normal de una parábola con h = - 1, k = 9 y, por
consiguiente, el vértice se encuentra en (-1, 9). Ya que a = - 1 < 0,
la parábola abre hacia abajo.
La ordenada en el origen de la gráfica de y = - x2 - 2x + 8 es el
término constante, 8. Para determinar las abscisas en el origen, se
resuelve la ecuación x2 - 2x + 8 = 0. Al factorizar se obtiene
(x + 4)(x - 2) = 0 y, por consiguiente, las abscisas en el origen son
x = - 4 y x = 2. Con esta información se traza el esquema de la
siguiente figura.
Si una parábola, y = ax2 + bx + c tiene abscisas en el origen x1 y x2,
como se ve en la siguiente figura para a < 0, entonces el eje de la
parábola es la recta vertical x = (x1 + x2)/2, que pasa por el punto
medio de (x1, 0) y (x2, 0). Por consiguiente, la abscisa h del vértice
(h, k) es h = (x1 + x2)/2.
Ejemplo 3.-
Localización del vértice de una parábola
Determinar las coordenadas del vértice de la parábola
y = 2x2 - 6x + 4.
Solución
Esta parábola se estudió en la determinación normal de una
parábola, y se encontró el vértice completando el cuadrado. Ahora
se emplea la fórmula del vértice, haciendo a = 2 y b = - 6, y se
obtiene la abscisa
− b − (−6) 6 3
=
= =
2a
2(2)
4 4
A continuación se determina la ordenada sustituyendo a x por 3/2
en la ecuación dada:
y = 2(3/2)2 - 6(3/2) + 4 = -1/2
Así, el vértice es (3/2 ,-1/2) (véase figura).
Como la gráfica de f(x) = ax2 + bx + c, cuando a ≠ 0 es una
parábola, se puede emplear la fórmula del vértice para ayudar a
localizar el valor máximo o mínimo de una función cuadrática.
Específicamente, como la abscisa del vértice V es - b/(2a), la
ordenada de V es el valor de f(- b/(2a)). Además, como la parábola
es cóncava hacia abajo si a < 0, y hacia arriba si a > 0, este valor es
el máximo o mínimo, respectivamente, de f.