r + r` dα

MATEMÁTICAS II.
Examen de SEPTIEMBRE 2004. Soluciones de CÁLCULO
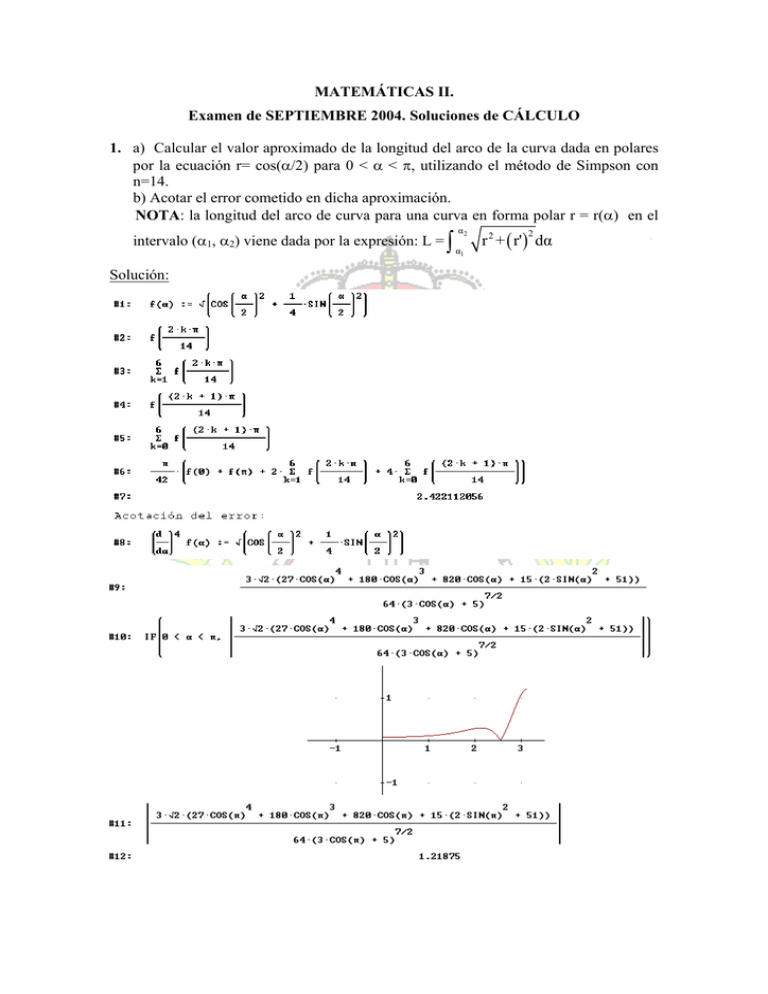
1. a) Calcular el valor aproximado de la longitud del arco de la curva dada en polares
por la ecuación r= cos(α/2) para 0 < α < π, utilizando el método de Simpson con
n=14.
b) Acotar el error cometido en dicha aproximación.
NOTA: la longitud del arco de curva para una curva en forma polar r = r(α) en el
intervalo (α1, α2) viene dada por la expresión: L =
Solución:
∫
α2
α1
r 2 + ( r') dα
2
4xy
, se pide:
x + y2 + 1
2. Sea la función f(x, y) =
2
a) Hallar la derivada direccional de f en P(1,1) y en la dirección del vector
u =(-1, -1) y deducir si en dicho punto y dirección la superficie crece, decrece o
presenta una curva de nivel.
b) Hallar la ecuación del plano tangente y de la recta normal en P(1,1).
c) Estudiar si la superficie tiene algún punto donde su plano tangente sea
horizontal.
Solución:
a) En el punto P(1,1) la función está definida y es continua y diferenciable por ser
cociente de funciones continuas y diferenciables, por tanto, la derivada direccional se
obtiene mediante la fórmula:
G
→
u
G
f’(P, u ) = ∇f (P) G
u
(
) (
) (
)
 4 y x 2 − y 2 − 1 4x x 2 − y 2 + 1 
→
 ∂f ∂f 
 = 4 , 4 
∇f (P) =  ,  =  −
,

2
2
 

 ∂x ∂y  P  x 2 + y 2 + 1
x2 + y2 +1 P  9 9 
G
u
1 
1
 1
(-1,-1) =  −
,−

G =
u
2
2
2

G
→
8
1 
u
4 4  1
G
< 0, luego en ese punto y
f’(P, u ) = ∇f (P) G =  ,   −
,−
=−
u
9 2
2
2
9 9 
dirección la superficie decrece.
b) La ecuación del plano tangente en P se calcula aplicando la fórmula:
(
)
 ∂f 
z – z0 =   (x – x0) +
 ∂x  P
 ∂f 
  (y – y0)
 ∂y  P
4
⇒ La ecuación del plano tangente en P es
3
4 4
4
z – = (x – 1) + (y – 1) ⇒ 4x + 4y – 9z + 4 = 0
3 9
9
La recta normal en P es la que pasa por P y su vector característico es (4, 4, -9), luego su
ecuación es:
x − 1 y − 1 3z − 4
x − 1 y − 1 z − 43
⇔
=
=
=
=
4
4
−9
4
4
− 27
c) Los planos horizontales son de la forma z = k, con k∈ℜ, luego ha de ocurrir que en
 ∂f 
 ∂f 
algún punto A sean   = 0 y   = 0 simultáneamente, es decir, hemos de
 ∂x  A
 ∂y  A
z0 = f(1,1) =
encontrar las soluciones de:
 4 y x 2 − y 2 − 1 4x x 2 − y 2 + 1 
−
 = (0,0), como el denominador es ≥ 1, basta calcular
,
2
2


2
2
x2 + y2 +1 
 x + y +1
los valores que anulan a los numeradores
(
(
) (
) (
)
)
Con DERIVE:
Solve([- 4·y·(x2 - y2 - 1=0, 4·x·(x2 - y2 + 1=0],[x,y]) y se obtiene:
[x = 0 ∧ y = 0, x = 0 ∧ y = î, x = 0 ∧ y = -î, x = î ∧ y = 0, x = -î ∧ y = 0]
La única solución real es x = 0, y = 0 ⇒ el único plano tangente horizontal es
z = f(0,0) ⇒ z =0
3. Sea z = f(x, y) una función real con derivadas parciales continuas en R2.
∂z
∂z
Considérese la expresión E = x
-y
∂y
∂x
Se efectúa el cambio de coordenadas cartesianas a polares (x, y) → (r, α)
 x = r cosα
. Se pide obtener E en función de r y α.

y
=
r
senα

(1.25 puntos)
Solución
∂z ∂z
,
en función de r y α.
∂y ∂x
Como z = f(x, y) = g(r, α) , el diagrama para aplicar la regla de la cadena es:
Debemos obtener las derivadas parciales
x
z
r
α
y
x
y
Aplicando la regla de la cadena:
∂z ∂z ∂r ∂z ∂α
=
⋅
+
⋅
∂x ∂r ∂x ∂α ∂x
∂z ∂z ∂r ∂z ∂α
=
⋅
+
⋅
∂y ∂r ∂y ∂α ∂y
∂r ∂α ∂r ∂α
,
,
,
∂x ∂x ∂y ∂y
r = x 2 + y 2
 x = r cosα

Despejando r y α en el sistema 
⇒ 
 y  , luego:
 y = r senα
α = arctg 
x

Necesitamos obtener las derivadas parciales
∂r
2x
=
=
∂ x 2 x2 + y2
∂r
2y
=
=
∂ y 2 x2 + y2
∂α
=
∂x
−
x
x 2 + y2
y
x 2 + y2
=
r cosα
= cosα
r
=
r senα
= senα
r
y
y
r senα
senα
x2 = −
=− 2 =−
2
2
2
r
x +y
r
y
1+  
x
1
x
r cosα cosα
∂α
x
. Por lo tanto:
=
=
=
=
2
2
2
2
∂y
r
+
x
y
r
y
1+  
x
1∂z
∂z ∂z ∂r ∂z ∂α ∂z
=
⋅
+
⋅
=
⋅ cos α −
⋅ sen α
∂x ∂r ∂x ∂α ∂x ∂r
r ∂α
1∂z
∂z ∂z ∂r ∂z ∂α ∂z
=
⋅
+
⋅
=
⋅ sen α +
⋅ cos α . Sustituyendo:
∂y ∂r ∂y ∂α ∂y ∂r
r ∂α
E=x
1∂z
∂z
∂z
∂ z

⋅ sen α +
⋅ cos α  - r sen
-y
= r cosα 
r ∂α
∂y
∂x
∂r

1∂z
 ∂z
∂ z
α
⋅ cos α −
⋅ sen α  =
r ∂α
∂r
 ∂α
4. Dada la función z = x3 + y3 + 3 x y, se pide hallar los extremos relativos y absolutos
de dicha función en el recinto A = {(x, y) ∈ R2 tales que x2 + y2 ≤ 8 }
Solución:
Estudiamos primero los extremos relativos en el interior de la región dada
Estudiamos ahora los extremos en la frontera x2 + y2 = 8
 x = 3senλ

5. Dada la curva r≡  y = 3cosλ+1 con λ∈ℜ, se pide:
z = 3λ

a) Estudiar si r presenta algún punto singular.
b) Estudiar si λ es el parámetro arco. En caso negativo hallar una parametrización
natural.
c) Hallar el triedro de Frenet en el punto P(0, -2,3π).
Solución:
a) Un punto es singular si la primera derivada se anula en dicho punto
 x = 3senλ
x' = 3cosλ


r ≡  y = 3cosλ+1 ⇒ r’ ≡  y' = −3senλ , como vemos z’ = 3 ≠ 0 para cualquier valor de
z' = 3
z = 3λ


λ, luego todos los puntos de r son regulares.
→
b) λ es el parámetro arco si r ' (λ ) = 1 para todo valor de λ
→
r ' (λ ) =
(3 cos λ) 2 + (−3senλ) 2 + 3 2 = 3 2 (cos 2 λ + sen 2 λ + 1) = 3 2 ≠ 1 para todo
valor de λ, luego λ no es el parámetro arco.
s=
λ →
λ
∫ 0 r ' (t ) dt = ∫ 0 3
2 dt = 3 2 λ ⇒ λ =
s
3 2
.
Una parametrización natural de r es:
s

=
x
3sen

3 2

s

+1
r(s) ≡ y = 3cos
3 2


s
z = 3
3 2

c) Usaremos la parametrización natural para obtener el triedro de Frenet
El punto P(0,-2, 3π) = r(s) ⇒ s = 3 2 π ⇒ P = r(3 2 π)
→
→

2
2
.
El vector tangente es:
t (3 2 π) = r ' (3 2π) =  −
,0,
2 
 2
El vector normal es:
→
n (3 2 π) =
→
r ' ' (3 2π)
→
= (0, 1,0 )
r ' ' (3 2π)
→
→

2
2

b (3 2 π) = = t (3 2 π) ∧ n (3 2 π) =  −
,0,2 
 2
6. a) Clasificar y resolver la siguiente ecuación diferencial con la función de Derive
específica para este tipo de ecuaciones:
(x4+ 2x2+ 2xy + 1)dx – (1 + x2)dy = 0.
b) Hallar la solución particular que pasa por el punto (2,3)
(No usar Dsolve ni Integrating_factor)
El vector binormal es:
→
Solución:
La ecuación puede escribirse en la forma
que corresponde a una ecuación lineal