Representación gráfica de funciones de una variable.

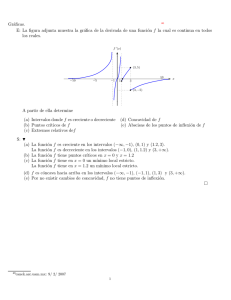
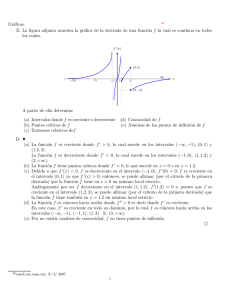
Dpto. Matemática Aplicada. E.T.S.A.M.
Cálculo.
[email protected].
CÁLCULO. REPRESENTACIÓN DE FUNCIONES.
1) DOMINIO.
Para hallar el dominio hay que tener en cuenta que:
i) si hay fracciones, el denominador no puede ser cero;
ii) si hay raı́ces de ı́ndice par, el radicando no puede ser negativo;
iii) si hay logaritmos, su argumento tiene que ser mayor estricto que cero.
2) SIMETRı́AS.
i) Una función es par (simétrica respecto del eje OY) cuando f (x) = f (−x).
ii) Una función es impar (simétrica respecto del origen) cuando f (x) = −f (−x).
3) PUNTOS CRı́TICOS E INTERVALOS DE CRECIMIENTO.
i) Condición necesaria: f 0 (x0 ) = 0.
ii) Condición suficiente: si la primera derivada distinta de cero es de orden par, en ese punto hay un extremo
local.
• Si f n (x0 ) > 0, en x0 hay un mı́nimo relativo o local.
• Si f n (x0 ) < 0, en x0 hay un máximo relativo o local.
También se pueden clasificar a partir de los intervalos de crecimiento y decrecimiento.
Los intervalos de crecimiento y decrecimento se construyen con los puntos crı́ticos, los puntos que no están en el
dominio y los puntos en los que la función no es derivable. Siempre son intervalos abiertos.
•
i) Si f 0 (x) > 0 en el intervalo, entonces la función es creciente en todo el intervalo.
ii) Si f 0 (x) < 0 en el intervalo, entonces la función es decreciente en todo el intervalo.
• Un punto crı́tico es máximo local cuando la función, a su izquierda es creciente y a su derecha, decreciente.
• Un punto crı́tico es mı́nimo local cuando la función, a su izquierda es decreciente y a su derecha, creciente.
• Si tiene el mismo comportamiento a la derecha y a la izquierda del punto crı́tico, en ese punto hay un punto
de inflexión de pendiente horizontal.
4) PUNTOS DE INFLEXIÓN Y CURVATURA.
i) Condición necesaria: f 00 (x0 ) = 0.
ii) Condición suficiente: si la primera derivada distinta de cero es de orden impar, en ese punto hay un punto
de inflexión.
También se pueden estudiar a partir de los intervalos de concavidad y convexidad.
Los intervalos de concavidad y convexidad se construyen con los puntos que verifican la condición necesaria,
los que no están en el dominio y los puntos en los que la función no es derivable. Siempre son intervalos
abiertos.
i. Si f 00 (x) < 0 en el intervalo, entonces la función es cóncava en todo ese intervalo.
ii. Si f 00 (x) > 0 en el intervalo, entonces la función es convexa en todo ese intervalo.
• Si en el punto obtenido en el apartado (i) cambia su curvatura, es decir, que la función pasa de cóncava
a convexa o viceversa, entonces en ese punto hay un punto de inflexión.
•
5) ASı́NTOTAS.
i) Horizontales: Si lim f (x) = b, en la recta y = b hay una ası́ntota horizontal.
x→±∞
ii) Verticales: Si lim f (x) = ±∞, en la recta x = a hay una ası́ntota horizontal.
x→a
iii) Oblı́cuas: La ecuación de una ası́ntota oblicua es y = mx + n.
f (x)
m = lim f 0 (x) o también m = limx→±∞
x→±∞
x
n = lim f (x) − mx.
x→±∞
Si hay ası́ntota horizontal NO puede haber ası́ntota oblı́cua.
1
Dpto. Matemática Aplicada. E.T.S.A.M.
Cálculo.
[email protected].
EJEMPLO
Representar gráficamente la función f (x) =
x2
.
x−1
Dominio:
IR − {1} . (En x = 1 se anula el denominador).
Simetrı́as:
x2
(−x)2
=
6= f (x) y 6= −f (x).
f (−x) =
−x − 1
−x − 1
Puntos crı́ticos e intervalos de crecimiento:
f 0 (x) =
2x·(x−1)−x2 ·1
(x−1)2
=
x2 −2x
(x−1)2
= 0 ⇔ x2 − 2x = 0 ⇔
x=0
x=2
Intervalos:
(−∞, 0)
f 0 (x) > 0 ⇒ f (x) %
0
(0, 1)
f (x) < 0 ⇒ f (x) &
(1, 2)
f 0 (x) < 0 ⇒ f (x) &
(2, ∞)
f 0 (x) > 0 ⇒ f (x) %
En x = 0 hay un máximo local (0, 0)
En x = 2 hay un mı́nimo local (2, 4)
Puntos de inflexión y curvatura:
(x−1)[(2x−2)(x−1)−2(x2 −2x)]
(x−1)4
−2(x−1)(x −2x)
=
f 00 (x) = (2x−2)(x−1)(x−1)
4
Intervalos de concavidad y convexidad:
2
2
=
2
(x−1)3
6= 0∀x ∈ IR − {1}
f 00 (x) < 0 ⇒ f (x) es cóncava.
f (x) > 0 ⇒ f (x) es convexa.

x2

lim
= +∞ 
x→+∞ x − 1
Horizontales:
⇒ No hay ası́ntotas horizontales.
2
x

lim
= −∞ 
x→−∞ x − 1
(−∞, 1)
(1, ∞)
Ası́ntotas:
Verticales:
00

x2

= +∞ 
x→1 x − 1
⇒En x = 1 hay una ası́ntota vertical.
x2

lim−
= −∞ 
x→1 x − 1
lim+
x2 − 2x
=1
x→+∞ (x − 1)2
Oblı́cuas:
x2
x
n = lim
− x = lim
=1
x→+∞ x − 1
x→+∞ x − 1
La recta y = x + 1 es ası́ntota obı́cua.
(Serı́a análogo en −∞)
m = lim
2







⇒