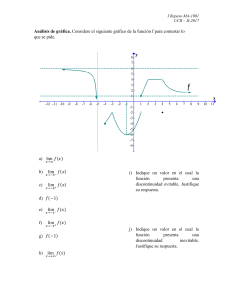
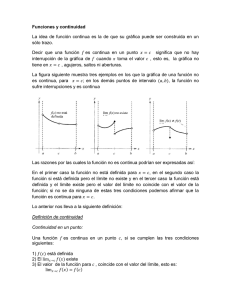
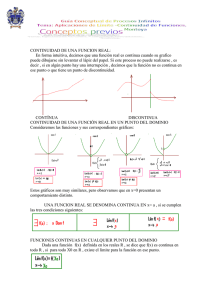
)( )( )3 )( )2 )()1 af xflim xflim af = ∃ ∃ condición 3ª la y/o condición
Anuncio

REPASO DERIVADAS Y CONTINUIDAD – 2º BT Def. (recuerda): Una función es continua en un punto a si cumple: 1)∃f (a ) 2)∃ lim f ( x) x→a 3) lim f ( x) = f (a) x→a Si se cumplen estas tres condiciones entonces la función es continua en el punto a. En caso de que no se cumpla alguna de ellas la función se dice que es discontinua en el punto a. 1.- Discontinuidad evitable ∃ lim f (x) x→ a Falla la 1ª condición y/o la 3ª condición 2.- Discontinuidad inevitable de salto ∃ lim+ f ( x ) x →a Pero son distintos ∃ lim− f ( x ) x →a 3.- Discontinuidad inevitable por no existir alguno o los dos límites laterales anteriores. Ejercicios (continuidad) : Estudiar la continuidad de las siguientes funciones: x + 1 f ( x) = x − 1 x2 − 4 f ( x) = x − 2 2 2 x + 1 x +1 f ( x) = 2 x −1 x − 1 x≥0 x<0 x≠2 x=2 x < −1 −1 ≤ x ≤ 0 0<x Ejercicios ( Derivadas ) : calcula las derivadas de las funciones... 1) f ( x) = x 2 (7 − 2 x) 2) f ( x) = (5 x 2 + 4 x − 3)(2 x − 7) 2x − 8 3) f ( x) = 3x + 5 x2 + 6 8x 9) f ( x ) = sen 4 x 8) f ( x) = 4) f ( x ) = 3 5 + 4 x 2 10) f ( x) = sen x 4 11) f ( x ) = sen 4 x 5) f ( x) = 5 5 x 2 + 2 x − 7 12) f ( x) = tag 5 x 1− x 1+ x 3 = f x x 7) ( ) ln x 13) f ( x) = ln 6) f ( x) = 1 + tagx 1 − tagx