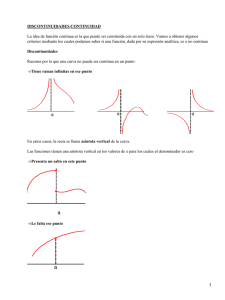
Funciones y continuidad La idea de función continua es la de que

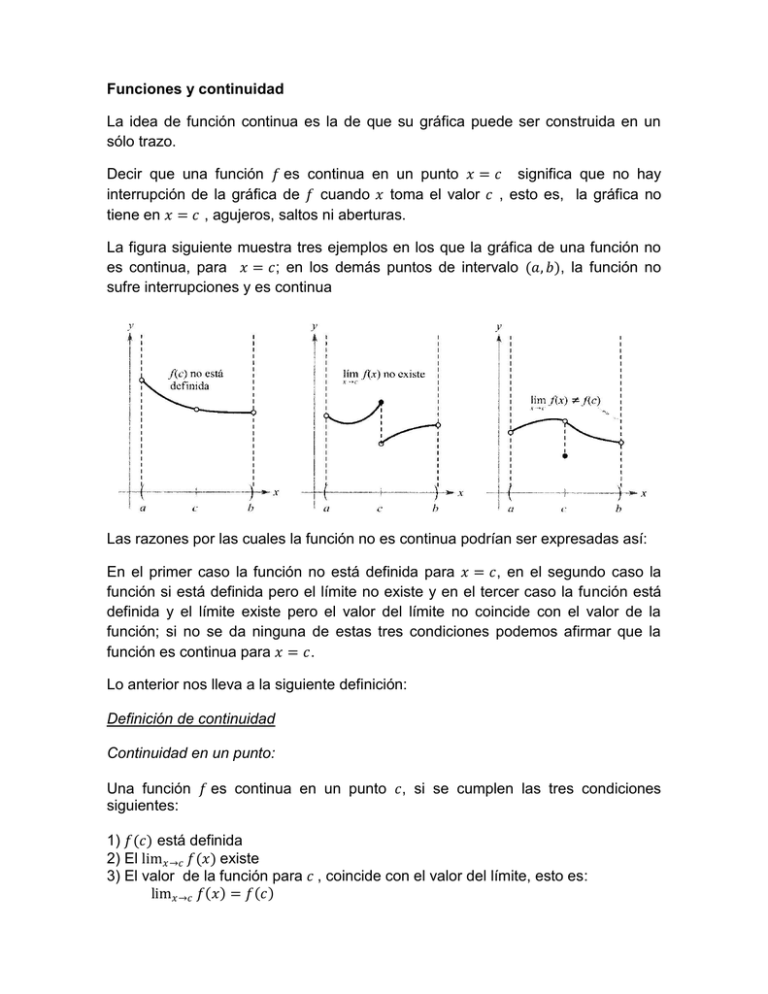
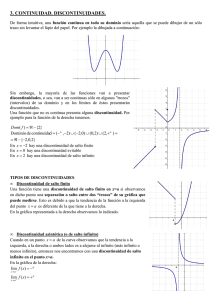
Funciones y continuidad
La idea de función continua es la de que su gráfica puede ser construida en un
sólo trazo.
Decir que una función 𝑓 es continua en un punto 𝑥 = 𝑐 significa que no hay
interrupción de la gráfica de 𝑓 cuando 𝑥 toma el valor 𝑐 , esto es, la gráfica no
tiene en 𝑥 = 𝑐 , agujeros, saltos ni aberturas.
La figura siguiente muestra tres ejemplos en los que la gráfica de una función no
es continua, para 𝑥 = 𝑐; en los demás puntos de intervalo (𝑎, 𝑏), la función no
sufre interrupciones y es continua
Las razones por las cuales la función no es continua podrían ser expresadas así:
En el primer caso la función no está definida para 𝑥 = 𝑐, en el segundo caso la
función si está definida pero el límite no existe y en el tercer caso la función está
definida y el límite existe pero el valor del límite no coincide con el valor de la
función; si no se da ninguna de estas tres condiciones podemos afirmar que la
función es continua para 𝑥 = 𝑐.
Lo anterior nos lleva a la siguiente definición:
Definición de continuidad
Continuidad en un punto:
Una función 𝑓 es continua en un punto 𝑐, si se cumplen las tres condiciones
siguientes:
1) 𝑓(𝑐) está definida
2) El lim𝑥→𝑐 𝑓(𝑥) existe
3) El valor de la función para 𝑐 , coincide con el valor del límite, esto es:
lim𝑥→𝑐 𝑓 𝑥 = 𝑓 𝑐
Continuidad en un intervalo abierto:
Se dice que una función es continua en un intervalo abierto (𝑎, 𝑏), si es continua
en todos los puntos del intervalo.
Una función que es continua en toda la recta real −∞, +∞ se llama continua en
todas sus partes
Si una función no es continua en un punto 𝑐 , se dice que tiene una discontinuidad
en 𝑐. Las discontinuidades se distribuyen en dos categorías: evitables e
inevitables. Una discontinuidad en un punto 𝑐 se denomina evitable si la función se
puede hacer continua definiendo apropiadamente 𝑓(𝑐).
Ejemplos gráficos:
A continuación se muestran varios ejemplos en los cuales se analiza la
continuidad de algunas funciones
2
Ejemplo 1: Analizar la continuidad de la función 𝑓 𝑥 = 𝑥
A la derecha podemos observar la
gráfica de la función
El dominio de 𝑓 es 𝑅 − 0 (los reales
exceptuando al cero)
La función es continua en todos los
valores de su dominio.
Para 𝑥 = 0 la función no está definida y
tampoco existe el límite de la función
cuando 𝑥 → 0
En 𝑥 = 0, 𝑓 tiene una discontinuidad
inevitable, esto es, no hay modo de
definir 𝑓 0 para que la función sea
continua
Ejemplo 2: Analizar la continuidad de la función 𝑔 𝑥 =
𝑥 2 −1
𝑥−1
A la derecha podemos observar la
gráfica de la función
El dominio de 𝑔 es 𝑅 − 1 (los
reales exceptuando al uno)
La función es continua en todos los
valores de su dominio.
Para 𝑥 = 1 la función no está
definida, aunque el límite de la
función cuando 𝑥 → 1 si existe y es
igual a 2
En 𝑥 = 1, 𝑔 tiene una discontinuidad
evitable, esto es, si se define
g 1 = 2, la “nueva” función es
continua
Ejemplo 3: Analizar la continuidad de la función 𝑓 𝑥 =
A la derecha podemos observar la
gráfica de la función
El dominio de 𝑓 es el conjunto 𝑅
(todos los reales)
Para todos los valores de 𝑥 la función
está definida, el límite de la función
existe y además coincide con el valor
de la función, por tanto la función es
continua en todos los valores 𝑥 de su
dominio.
𝑓 es continua en toda la recta real
(− ∞, +∞)
𝑥 + 2, 𝑠𝑖 𝑥 ≤ −1
𝑥 2 , 𝑠𝑖 𝑥 > −1
Ejemplo 4: Analizar la continuidad de la función 𝑓 𝑥 = cos 𝑥
A la derecha podemos observar la
gráfica de la función
El dominio de 𝑓 es el conjunto 𝑅
(todos los reales)
Para todos los valores de 𝑥 la función
está definida, el límite de la función
existe y además coincide con el valor
de la función, o sea
lim𝑥→𝑐 cos 𝑥 = cos(𝑐), por tanto la
función es continua en todos los valores
𝑥 de su dominio.
𝑓 es continua en toda la recta real
(− ∞, +∞)
Ejercicios
propuestos
En cada una de las siguientes funciones, hallar los valores de 𝑥 (si existe alguno)
en los que la función no es continua. ¿Qué discontinuidad es evitable?
Sugerencia: En algunos casos es conveniente utilizar winplot u otro graficador
para el análisis de la continuidad de las funciones
𝑥
1. 𝑓 𝑥 = 𝑥 − 1
7.
𝑓 𝑥 = 𝑥 2 −1
2. 𝑕 𝑥 = 𝑥 2 − 2𝑥 + 1
8.
𝑓 𝑥 = 𝑥 2 −1
9.
𝑓 𝑥 = 𝑠𝑒𝑛𝑥
3. 𝑓 𝑥 =
𝑥 2 −2𝑥+1
1
𝑥−1
1
4. 𝑓 𝑥 = 𝑥−1
10.
𝑓 𝑥 =
𝑥, 𝑥 ≤ 1
𝑥2 , 𝑥 > 1
11.
𝑓 𝑥 =
−2𝑥 + 3, 𝑥 < 1
𝑥2, 𝑥 ≥ 1
𝑥
5. 𝑓 𝑥 = 𝑥 2 +1
1
1
6. 𝑕 𝑥 = 𝑥 2 +1
12
𝑔 𝑥 =
𝑥 + 1, 𝑥 ≤ 2
3 − 𝑥, 𝑥 > 2
2