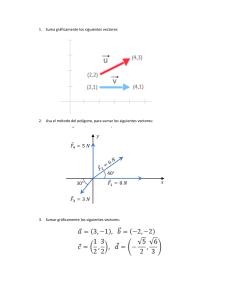
Construyendo Soluciones - En los siguientes planteamientos

Construyendo Soluciones
-
En los siguientes planteamientos, proceda a construir la solución y describir
el proceso de manera paralela.
-
Transcribir en un documento de procesador de textos, el proceso seguido
para el desarrollo de los planteamientos.
-
En caso de que las representaciones gráficas sean realizadas por medio de
un software, pegar en el documento, una copia de tal representación.
-
Adjuntar el archivo en formato PDF en la tarea: Construyendo Aprendizaje 1


a  (x ,2y ,3z) ,
1) Sean

b  (x , x ,2y) y


a  b  (6 ,5,2) .
¿Cuáles
serán
las

coordenadas de los vectores a y b ?


2) Dados e : (1,2,5) y f : (3,2,1) , proceda a:




a. Determinar e  f y representar gráficamente.
b. Determinar f  e y representar gráficamente.




c. Argumentar: ¿Podrían ser los vectores e  f y f  e , equipolentes?


3) Sean c  (1,2,3) y d  (1,4 ,3) , proceda a:




a. Determinar y representar gráficamente c  d
b. Determinar y representar gráficamente d  c


c d
c. Indicar: ¿Serán los vectores
Argumente


y d  c , vectores opuestos?




d. Mencionar: ¿Podrían ser los vectores c  d y d  c , equipolentes?
Argumente.


4) Sea s : (1, 1 2 ,3) y  un escalar, si r : (1 4 , 1 8 , 3 4) y


r    s ¿Cuál será el
valor de  ?





5) Sean c   a   b , a : (1,2, 3 2 ) y b : (3,  2 3 ,1) , los escalares   2 y

  1 . ¿Cuál será la coordenada del vector c ?