Tema 8. Resolución numérica de ecuaciones

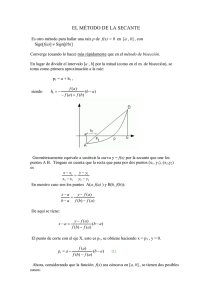
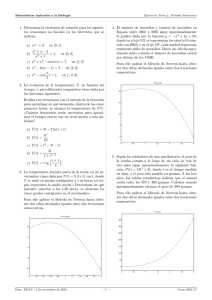
Tema 8. Resolución numérica de ecuaciones
1.- Bisección.
xn =
xn =
an +bn
2
an + bn
Criterio: signos diferentes
2
f (an ) · f (bn ) < 0
2.- a) Regula falsi.
♣ ¿De dónde viene la fórmula?
.- En cada iteración sustituimos la función por la recta que interpola en (an , f (an ) y (bn , f (bn ).
y − f (an ) =
f (bn ) − f (an )
(x − an )
bn − an
.- Se calcula el valor que anula la función lineal.
xn = an −
(bn −an )f (an )
f (bn )−f (an )
Criterio de elección: f (an ) · f (bn ) < 0
b) Secante.
¿De dónde viene la fórmula?
Para hallar xn+1 , se interpola, en este caso, en (xn−1 , f (xn−1 )) y (xn , f (xn ))
textitCriterio de elección f (a) · f (b) < 0. Sólo al principio. x0 = a,
x1 = b
xn+1 = xn −
(xn −xn−1 )f (xn )
f (xn )−f (xn−1 )
3.- Newton Rhapson.
xn+1 = xn −
f (xn )
f 0 (xn )
.- Condiciones: f derivable, f 0 6= 0 y f 00 no cambia de signo.
.- Criterio de elección: f (a) · f (b) < 0. Sólo al principio
¿De dónde viene la fórmula? Esta vez el papel de la función la toma, no una recta interpoladora sino la tangente.
y − f (xn ) = f 0 (xn )(x − xn )
Ejercicios
1. Encontrar una aproximación a
√
3
2 mediante el método de la bisección. (5 iteraciones). Resolver x3 − 2 = 0
2. Aplicar el método de bisección para encontrar las soluciones de x4 − 2x3 − 4x2 + 4x + 4 = 0 en los intervalos
[−2, −1] y [0, 2]. ((4 iteraciones))
3. Usar el método de bisección para encontrar una solución de 2 + cos (ex − 2) − ex = 0. (4 iteraciones)
4. Aproximar mediante el método de la regula falsi la raíz de la ecuación x3 − 2x2 − 5 = 0 en el intervalo [1, 4],
realizando tres iteraciones y utilizando cinco cifras decimales.
√
5. Utilizar el método de la regula falsi para aproximar una raíz de la ecuación x sen x − x3 + 2 = 0 en el intervalo
[1,2], realizando cuatro iteraciones.
6. Resolver por el método de la secante (4 iteraciones):
a) x ln x − 10 = 0
b) sen x − cosec x + 1 = 0
c) ex + 2−x + 2 cos x − 6 = 0
7. La ecuación x − 9−x = 0 tiene una solución en [0,1]. Encontrarla mediante el método de la secante, aplicando
cuatro iteraciones.
8. Hallar la abscisa del punto de inflexión de la curva
y = e−x ln x, x > 0
con cinco dígitos decimales exactos, tomando como valor inicial x0 = 2. Usa Newton-Rhapson.
√
9. Encontrar el punto de intersección de las gráficas de las funciones y = x2 + 1, y = tg x, 0 < x < π/2, tomando
como punto inicial x0 = 1 y efectuando tres iteraciones. Usa Newton-Rhapson.
10. Utilizar el método de Newton–Raphson para dar una aproximación de la solución de 1 − ln x = 0, tomando como
valor inicial x0 = 1 y efectuando cuatro iteraciones. Si consideramos e = 20 718281828, dar una estimación del
error cometido.
11. Obtener una solución de la ecuación
e−x + x2 − 10 = 0
aplicando el método de Newton–Raphson y efectuando cuatro iteraciones.