Tema 3 VARIABLE ALEATORIA DISCRETA. PRINCIPALES

Probabilidad y Estadística (I.I.)
Tema 3
Tema 3
VARIABLE ALEATORIA DISCRETA.
PRINCIPALES DISTRIBUCIONES
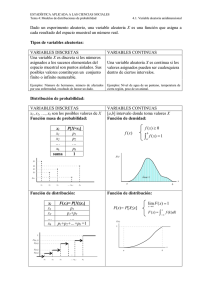
1.- Definición de variable aleatoria discreta.
Normalmente, los resultados posibles (espacio muestral Ω) de un experimento aleatorio no son
valores numéricos. Por ejemplo, si el experimento consiste en lanzar de modo ordenado 2
monedas al aire para observar el número de caras (C) y cruces (X) que se obtienen, el espacio
muestral asociado a dicho experimento aleatorio sería:
Ω = {CC, CX, XC, XX}
En Estadística resulta más fácil utilizar valores numéricos en lugar de trabajar directamente
con los elementos de un espacio muestral como el anterior. Así, preferimos identificar los
sucesos {CX, XC} con el valor numérico 1, que representa el número de caras obtenidas al
realizar el experimento. De este modo aparece el concepto de variable aleatoria.
Sea (Ω, ℘(Ω), P) un espacio de probabilidad. Una función
X: Ω → ℜ
ω → X(ω)= xω
es una variable aleatoria, es decir, las variables aleatorias unidimensionales son funciones
cuyos valores dependen del resultado de un experimento aleatorio. Una variable aleatoria es
una función que asocia un número real y sólo uno xω, a cada suceso elemental ω del espacio
muestral (Ω ) de un experimento aleatorio.
Las variables aleatorias discretas son aquellas que sólo pueden tomar un número de valores
finito o infinito numerable.
X: Ω → Ν
ω → X(ω)= xω
Se representan mediante letras mayúsculas y pueden tomar n posibles valores:
X = { x1, x2, ... , xi , ... , xn }
Ejemplo:
Experimento aleatorio: “Lanzar una moneda al aire dos veces”
Espacio muestral: Ω = {CC, CX, XC, XX}
Sucesos elementales: {CC}, {CX}, {XC}, {XX}
Se define la variable X: Nº de caras obtenidas
Asignación de números reales: (CC, 2); (CX, 1); (XC, 1); (XX, 0)
Por tanto, la variable X viene definida por los valores: 0, 1, 2
En el ejemplo anterior, X = {0, 1, 2}
La v.a.d., X, queda caracterizada por la función de probabilidad, f(x) = P(X = x), y por la función
de distribución, F(x) = P(X ≤ x).
1
Probabilidad y Estadística (I.I.)
Tema 3
2.- Función de probabilidad, f(x)
(Ω, ℘(Ω), P) un espacio de probabilidad, X v. a. d., y {xi}i=1..∞ los valores que toma. Se llama
función de probabilidad, f(x), a la función que indica la probabilidad de cada posible valor de la
v. a. d. X, es decir:
f: N → [0, 1]
∀ i=1, ..,∞
xi → f(xi) = P(X = xi) = pi =P[{ω t.q. X(ω)=xi]
y que verifica:
(i) 0 ≤ f(xi) ≤ 1
(ii) ∑ f(xi) = 1
Si xi no es uno de los valores que puede tomar X, entonces f(xi)=0. Gráficamente se representa
mediante un diagrama de barras análogo al de distribución de frecuencias relativas para
variables discretas.
X
f(xi)
0
0,25
1
0,50
f (x)
Con los datos del ejemplo anterior:
2
0,25
2
3.- Función de distribución, F(x)
0 1
Sea (Ω, ℘(Ω), P) un espacio de probabilidad, X v. a. d., {xi}i=1..∞ los valores que toma y {pi}i=1..∞
⊂ ℜ la función de probabilidad de X. Se llama función de distribución (acumulativa) de la v.a.d.
X, F(x), a la probabilidad de que X sea menor o igual que x; es decir:
F: N → [0, 1]
xi → F(xi) = P(X ≤ xi) = P[{ω t.q. X(ω) ≤ xi]
F(xi) = P(X ≤ xi) =
∑ f (x
x j ≤ xi
Que cumple las siguientes propiedades:
(i) F(-∞)=0
(ii) F(xmin) = f(x1)
2
j
)
Probabilidad y Estadística (I.I.)
Tema 3
(iii) F(xmax) = 1
(iv) F(∞)=1
(v) F es monótona no decreciente, es decir, si xi ≤ xj entonces F(xi) ≤ F(xj)
(vi) F es continua a derecha, tiene límites a izquierda y es constante en [xi-1, xi), donde toma el
valor
∑ f (x
k ≤i
k
)
(vii) P(X > x) = 1 - P(X ≤ x) = 1 - F(x)
(viii) P(xi ≤ X ≤ xj) = F(xj) - F(xi-1)
Gráficamente resulta en la función escalera
X
F(xi)
0
0,25
1
0,75
F (x)
Continuando con el ejemplo anterior:
2
1,00
0
1
2
4.- Características de las v. a. discretas
Se trata de resumir la información de una variable aleatoria en un conjunto de medidas
(números).
De forma análoga a lo que se hizo en el tema de Estadística Descriptiva, podemos definir para
las variables aleatorias medidas de centralización, dispersión, simetría y forma. Por su interés
especial, nos vamos a centrar en dos medidas sobre variables aleatorias que son: la esperanza
matemática, que desempeña un papel equivalente al de la media, y la varianza.
Esperanza:
Sea X v. a. El valor esperado o esperanza matemática de X, denotada por E(X) o por µ, se
define como:
3
Probabilidad y Estadística (I.I.)
Tema 3
n
E ( X ) = ∑ xi f ( xi )
i =1
E(X) no es una función de x, es un valor fijo que depende de la distribución de probabilidad de
X. E(X) está medida en las mismas unidades que X. Si X es una v.a. con función de probabilidad
simétrica respecto a un punto x=a, entonces E(X)=a.
Propiedades de la esperanza:
(i) Si C es una constante, entonces E(C)=C.
(ii) Linealidad: E(aX+b)=aE(X)+b, ∀a, b ∈ℜ
[
n
] ∑ g ( xi ) f ( xi )
(iii) Si g(X) es una función de X, entonces: E g ( X ) =
i =1
(iv) Si g(X), h(X) son funciones de X, entonces E[g(X)+h(X)]=E[g(X)]+ E[h(X)]
(v) |E[g(X)]| ≤ E[|g(X)|]
(vi) Si X e Y son v. a. independientes Î E[X.Y]=E[X].E[Y]
Varianza:
Sea X v. a. La varianza de X se denota con Var(X) o σ2 y se define como
[
] ∑ (x − E[X ])
Var [X ] = E ( X − E [X ]) =
2
i
2
⋅ f ( xi )
i
La raíz cuadrada positiva de la varianza se llama desviación típica y se denota con σ. Tanto la
varianza como la desviación típica miden la dispersión de la v.a. respecto a su media.
Observaciones:
- La varianza y la desviación típica son cantidades positivas.
- La desviación típica está medida en las mismas unidades que la v.a.
Propiedades de la varianza:
(i) Si C es una constante, Var(C)=0
(ii) Var(X) = E(X2) - E2(X)
(iii) Si a y b son constantes: Var(aX + b) = a2 Var(X)
(iv) Si X e Si X e Y son v.a. independientes Î V(X+Y) = V(X) + V(Y)
La desviación media se define como la esperanza de |X-µ|.
5.- Principales distribuciones de las v. a. discretas:
En la práctica, la función de probabilidad de la mayoría de las variables discretas se ajusta a un
modelo teórico expresado mediante una fórmula concreta. Veremos los más habituales.
Distribución de Bernouilli Be(p)
La distribución de Bernouilli se aplica cuando se realiza una sola vez un experimento que tiene
únicamente dos posibles resultados (éxito o fracaso), por lo que la variable sólo puede tomar
dos valores: el 1 (éxito) y el 0 (fracaso).
Definimos la v.a.:
4
Probabilidad y Estadística (I.I.)
Tema 3
Al haber únicamente dos soluciones se trata de sucesos complementarios:
A la probabilidad de éxito se le denomina "p"
A la probabilidad de fracaso se le denomina "q"
Verificándose que:
p + q = 1
Así P(X=1)=p y P(X=0)=1-p=q.
Además E(X)=p, Var(X)=pq.
Ejemplo: Probabilidad de salir cara al lanzar una moneda al aire (sale cara o no sale);
probabilidad de ser admitido en una universidad (o te admiten o no te admiten); probabilidad
de acertar una quiniela (o aciertas o no aciertas)
Distribución Binomial B(n,p)
La distribución binomial parte de la distribución de Bernouilli. Se aplica cuando se realizan un
número "n" de veces el experimento de Bernouilli, siendo cada ensayo independiente del
anterior. Realizamos el experimento anterior n veces de forma independiente, y definimos la
v.a.:
X= “Número de éxitos obtenidos en las n realizaciones”
que puede tomar los valores k=0,1,…,n
0: si todos los experimentos han sido fracaso
n: si todos los experimentos han sido éxitos
con probabilidades:
La distribución de probabilidad de este tipo de distribución expresada de otra forma:
donde
" k " es el número de aciertos
" n" es el número de ensayos.
" p " es la probabilidad de éxito
E(X) = n.p
Var(X) = n.p.(1-p)=n.p.q
Ejemplo:
¿Cuál es la probabilidad de obtener 6 caras al lanzar una moneda 10 veces?
La fórmula quedaría:
Luego,
P (x = 6) = 0,205
5
Probabilidad y Estadística (I.I.)
Tema 3
Es decir, se tiene una probabilidad del 20,5% de obtener 6 caras al lanzar 10 veces una
moneda.
No siempre es necesario aplicar la fórmula para obtener la función de probabilidad asociada a
un valor de la variable. Existen tablas donde se puede consultar el valor de f (xi). La tabla de la
Binomial tiene la siguiente estructura:
Dado X → B (x; n; p), para buscar una f (x):
1ª columna: valor de n
2ª columna: posibles valores de X: 0, 1, …, n
3ª columna: valor de f(x) bajo diferentes valores de p (aparece en porcentajes, por brevedad.
El signo +significa que hay más de tres ceros)
Nota: Cuando n > 17, f (xi) puede aproximarse mediante el modelo normal (lo veremos en el
próximo tema)
Ejemplo:
P(X = 1) = 0,02 bajo X → B (x; 2; 0,01)
Ejemplo:
Un sujeto responde a un test 4 preguntas de tipo V/F al azar.
1) Elabore el modelo de distribución para la variable X (nº de aciertos al azar)
X ∈B (n = 4, p= 0,50)
X→01234
f(x)→ 0,0625 0,250 0,375 0,250 0,0625
2) ¿Cuál es la probabilidad de que acierte al menos 3 preguntas?
P(X ≥ 3) = P(X = 3) + P(X = 4) = 0,250 + 0,0625 = 0,3125 (coincide con tablas)
O también P(X ≥ 3) = 1- P(X ≤ 2) = 1 - (0,062 + 0,250 + 0,375) = 1 - 0,687 = 0,313
3) Valor esperado: E(X) = n · p= (4) (0,50) = 2
4) Varianza: s2(X) = n · p .(1 - p) = (4) (0,50 · 0,50) = 1
5) ¿Cuál es la probabilidad de que acierte como máximo 2 preguntas?
P(X ≤ 2) = F(2) = 0,0625 + 0,250 + 0,375 = 0,6875
6) ¿Cuál es la probabilidad de que acierte entre 1 y 3 preguntas (ambas inclusive)?
P(1 ≤ X ≤ 3) = F(3) - F(0) = 0,9375 - 0,0625 = 0,875
7) ¿Cuál es la probabilidad de que acierte más de 2 preguntas?
P(X > 2) = P(X ≥ 3) = 1 - P(X ≤ 2) = 1 – 0,6875 = 0,3125
Distribución de Poisson P(λ)
6
Probabilidad y Estadística (I.I.)
Tema 3
Esta distribución aparece en algunos procesos que tienen una dimensión temporal o espacial,
como el número de llamadas telefónicas que recibe un servicio de atención a urgencias durante
un intervalo de tiempo determinado, o el número de cultivos infectados por una plaga en una
cierta región geográfica.
En este tipo de experimentos los éxitos buscados son expresados por unidad de área, tiempo,
pieza, etc,:
- nº de defectos de una tela por m2
- nº de aviones que aterrizan en un aeropuerto por día, hora, minuto, etc, etc.
- nº de bacterias por cm2 de cultivo
- nº de llamadas telefónicas a un conmutador por hora, minuto, etc, etc.
- nº de llegadas de embarcaciones a un puerto por día, mes, etc, etc.
X= “Número de éxitos obtenidos por unidad de tiempo o de espacio”
Para determinar la probabilidad de que ocurran k éxitos por unidad de tiempo, área, o
producto, la fórmula a utilizar sería:
donde:
p(x=k) = probabilidad de que ocurran k éxitos cuando el número promedio de ocurrencia de
ellos es λ
λ = media o promedio de éxitos por unidad de tiempo, área o producto
e = 2.718
x = variable que nos denota el número de éxitos que se desea que ocurra
E(X)=λ
Var(X)=λ
Hay que hacer notar que en esta distribución el número de éxitos que ocurren por unidad de
tiempo, área o producto es totalmente al azar y que cada intervalo de tiempo es independiente
de otro intervalo dado, así como cada área es independiente de otra área dada y cada producto
es independiente de otro producto dado. En estas condiciones el proceso de Poisson, que mide
el número de éxitos en un intervalo de tiempo t, en lugar de por unidad de tiempo, vendría dado
por
A λ se le llama tasa de emisión (por unidad de tiempo).
Ejemplo:
Si un banco recibe en promedio 6 cheques sin fondo por día, ¿cuáles son las probabilidades de
que reciba, a) cuatro cheques sin fondo en un día dado, b) 10 cheques sin fondos en cualquiera
de dos días consecutivos?
7
Probabilidad y Estadística (I.I.)
Tema 3
a) x = variable que nos define el número de cheques sin fondo que llegan al banco en un día
cualquiera = 0, 1, 2, 3, ....., etc
λ = 6 cheques sin fondo por día
p( x = 4 ,λ = 6 ) =
( 6 )4 ( 2.718 )−6 ( 1296 )( 0.00248 )
=
= 0.13392
4!
24
b) x= variable que nos define el número de cheques sin fondo que llegan al banco en dos días
consecutivos = 0, 1, 2, 3, ......, etc
λ = 6 x 2 = 12 cheques sin fondo en promedio que llegan al banco en dos días consecutivos
Nota: λ siempre debe de estar en función de x siempre o dicho de otra forma, debe “hablar”
de lo mismo que x.
p( x = 10 ,λ = 12 ) =
( 12 )10 ( 2.718 )−12 ( 6.1917364Ε10 )( 0.000006151 )
=
= 0.104953
10!
3628800
Ejemplo:
En la inspección de hojalata producida por un proceso electrolítico continuo, se identifican 0.2
imperfecciones en promedio por minuto. Determine las probabilidades de identificar a) una
imperfección en 3 minutos, b) al menos dos imperfecciones en 5 minutos, c) cuando más una
imperfección en 15 minutos.
a)
x = variable que nos define el número de imperfecciones en la hojalata por cada 3
minutos = 0, 1, 2, 3, ...., etc.
λ = 0.2 x 3 =0.6 imperfecciones en promedio por cada 3 minutos en la hojalata
p( x = 1,λ = 0.6 ) =
( 0.6 )1( 2.718 )−0.6 ( 0.6 )( 0.548845 )
=
= 0.329307
1!
1
b)
x = variable que nos define el número de imperfecciones en la hojalata por cada 5
minutos = 0, 1, 2, 3, ...., etc
λ = 0.2 x 5 =1 imperfección en promedio por cada 5 minutos en la hojalata
⎛ ( 1 )0 ( 2.718 )−1 ( 1 )( 2.718 )−1 ⎞
⎟⎟ =
p( x = 2,3,4,etc....λ = 1 ) = 1 − p( x = 0,1,λ = 1 ) = 1 − ⎜⎜
+
0!
1!
⎠
⎝
=1-(0.367918+0.367918) = 0.26416
c)
x = variable que nos define el número de imperfecciones en la hojalata por cada 15
minutos = 0, 1, 2, 3, ....., etc.
λ = 0.2 x 15 = 3 imperfecciones en promedio por cada 15 minutos en la hojalata
p( x = 0,1,λ = 3 ) = p( x = 0,λ = 3 ) + p( x = 1,λ = 3 ) =
= 0.0498026 + 0.149408 = 0.1992106
8
( 3 )0 ( 2.718 )−3 ( 3 )1( 2.718 )−3
+
=
0!
1!
Probabilidad y Estadística (I.I.)
Tema 3
También se puede considerar esta distribución como una aproximación de la binomial cuando n↑
y p↓, pero el producto n.p permanece constante. Cuando en una distribución binomial se realiza
el experimento un número "n" muy elevado de veces y la probabilidad de éxito "p" en cada
ensayo es reducida, manteniéndose constante n.p, entonces se aplica el modelo de distribución
de Poisson.
Realizamos indefinidamente el experimento y definimos la v.a.:
X= “Número de éxitos obtenidos”
que puede tomar los valores k=0,1,2,…
Al igual que ocurría con la binomial, los valores acumulados de la distribución de Poisson se
encuentran tabulados para que resulte más fácil su manejo.
Ejemplo:
En una concurrida intersección de tráfico, la probabilidad de que un automóvil tenga un
accidente de tráfico es muy escasa, digamos de 0,0001. Sin embargo, durante cierta parte del
día (entre las 4:00 pm y las 6:00 pm) un gran número de automóviles pasa por esa intersección,
digamos unos 1000. En dichas condiciones, ¿cual es la probabilidad de que dos o más accidentes
ocurran durante ese período?
X= nº accidentes en 1000 coches
X≈B(1000, 0.0001)
P(X ≥ 2)
Como la probabilidad " p " es menor que 0,1, y n ≥ 30, entonces aplicamos el modelo de
distribución de Poisson y podríamos aproximar por X ≈ P(0.1)
P(X ≥ 2) = 1 – P(X < 2) = 1 – P(X ≤ 1) = 1 – 0.9953 = 0.0047
Distribución Geométrica G(p)
Realizamos el experimento de forma independiente hasta que obtenemos el primer éxito, y
definimos la v.a.:
Y=”Número de experimentos hasta obtener el primer éxito”
que toma los valores k=1,2,3,… con probabilidades:
donde se tiene que E(Y)=1/p y Var(Y)=(1-p)/p2.
Ejemplo:
Una vía de una ciudad tiene seis cruces regulados por semáforos. La probabilidad de que al
pasar un vehículo un semáforo esté verde es de 0.60. ¿ Cuál es la probabilidad de atravesar
dicha vía en verde, encontrándose rojo solamente el último semáforo? Se supone que la
regulación de los semáforos es tal que estos son independientes entre sí.
X = nº de semáforos que debemos atravesar hasta encontrar el primero rojo
X≈ G(0.4)
P(X=6) = 0.65 0.4 = 0.0311
9
Probabilidad y Estadística (I.I.)
Tema 3
Distribución Binomial Negativa BN (n,p)
Realizamos el experimento de forma independiente hasta obtener n éxitos y definimos la v.a.:
X= “Número de fracasos antes del n-ésimo éxito”
que puede tomar los valores k=0,1,2,…
Además E(X)=n(1-p)/p y Var(X)=n(1-p)/p2.
Ejemplo:
En los play-off de la NBA americana, el vencedor de cada eliminatoria final es el equipo que
logre primero la 4ª victoria en un total de 7 confrontaciones. ¿Cuál es la probabilidad de que un
equipo dispute como mucho 6 partidos, si su porcentaje de partidos ganados es del 60%?
P=probabilidad de éxito =0.6
X= nº fracasos hasta obtener la 4ª victoria X ≈ BN(4,0.6)
P(X ≤ 2)=P(X=0) + P(X=1) + P(X=2) = 0.1296 + 0.20736 + 0.20736 = 0.54432
Distribución Hipergeométrica H(N,D,n)
La distribución hipergeométrica es el modelo que se aplica en experimentos donde, al igual que
en la distribución binomial, en cada ensayo hay tan sólo dos posibles resultados: éxito o
fracaso. Pero se diferencia de la distribución binomial en que los distintos ensayos son
dependientes entre sí (no hay reemplazamiento).
Supongamos que tenemos un lote de N piezas de las cuales D son defectuosas (D ≤ N). Extraigo
una muestra de n piezas (sin reemplazamiento) y defino la v. a.:
X= “Número de defectuosas en la muestra”
que puede tomar los valores k=max{0,n+D-N},1,…,min{D,n}
Además E(X) = nD/N y Var(X) = np(1-p)[(N-n)/(N-1)] con p = D/N = proporción de
defectuosas.
Nota: Cuando se realiza un muestreo, éste puede ser con o sin reemplazamiento. Si es con
reemplazamiento utilizaremos la distribución binomial para contar el número de éxitos y si es
sin reemplazamiento utilizaremos la distribución hipergeométrica. Además, si N es grande
respecto a n, la binomial aproximará a la hipergeométrica (la aproximación es buena cuando
n/N < 0.1).
Ejemplo:
10
Probabilidad y Estadística (I.I.)
Tema 3
En una urna hay 7 bolas blancas y 5 negras. Se sacan 4 bolas ¿Cuál es la probabilidad de que 3
sean blancas?
Entonces:
N = 12; N-D = 5; D = 7; k = 3; n = 4
Si aplicamos el modelo:
Por lo tanto, P (x = 3) = 0,3535. Es decir, la probabilidad de sacar 3 bolas blancas es del 35,3%.
Pero este modelo no sólo se utiliza con experimentos con bolas, sino que también se aplica con
experimentos similares:
Ejemplo:
En una fiesta hay 20 personas: 14 casadas y 6 solteras. Se eligen 3 personas al azar ¿Cuál es la
probabilidad de que las 3 sean solteras?
Por lo tanto, P (x = 3) = 0,0175. Es decir, la probabilidad de que las 3 personas sean solteras es
tan sólo del 1,75%.
Distribución Multinomial
La distribución multinomial es similar a la distribución binomial, con la diferencia de que en
lugar de dos posibles resultados en cada ensayo, puede haber múltiples resultados:
La distribución multinomial sigue el siguiente modelo:
con n= x1+x2+x3+…
Donde:
X1 = x1: indica que el suceso X1 aparezca x1 veces
n: indica el número de veces que se ha repetido el experimento
n!: es factorial de n
p1: es la probabilidad del suceso X1
Ejemplo:
En una fiesta, el 20% de los asistentes son españoles, el 30% franceses, el 40% italianos y el
10% portugueses. En un pequeño grupo se han reunido 4 invitados: ¿cual es la probabilidad de
que 2 sean españoles y 2 italianos?
11
Probabilidad y Estadística (I.I.)
Tema 3
Aplicamos el modelo:
Luego
P = 0,0384
Por lo tanto, la probabilidad de que el grupo esté formado por personas de estos países es tan
sólo del 3,84%.
Distribucion Multihipergeométrica
La distribución multihipergeométrica es similar a la distribución hipergeométrica, con la
diferencia de que en lugar de dos posibles resultados en cada ensayo, puede haber múltiples
resultados (en la urna, en lugar de haber únicamente bolas de dos colores, hay bolas de
diferentes colores).
La distribución multihipergeométrica sigue el siguiente modelo:
siendo n = x1 + x2 + x3 + ….
Donde:
X1 = x1: indica que el suceso X1 aparezca x1 veces
N1: indica el número de elementos del tipo X1 que existen
N: es el número total de elementos que existen
n: es el número total de elementos que se extraen
Ejemplo:
En una caja de lápices hay 10 de color amarillo, 3 de color azul y 4 de color rojo. Se extraen 7
lápices, ¿cual es la probabilidad de que 5 sean amarillos y 2 rojos?
Aplicamos el modelo:
Luego
P = 0,0777
Por lo tanto, la probabilidad de que los 5 lápices sean de los colores indicados es del 7,77%.
12