Medidas de Tendencia Central: Guía para Tercero Básico

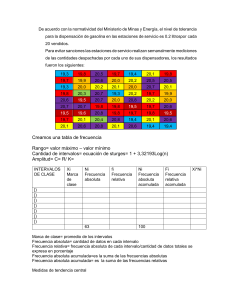
7.2 Medidas de tendencia central
Muestra. Las calificaciones ordenadas de los estudiantes de tercero básico sección
“A” el área de comunicación y lenguaje
41,48,56,68,70,73,74,83,84,85,85,86,86,86,87,87,89,90,91,91,92,92,93,93,93,94,9
6,96,98
Media aritmética o promedio: Es el valor promedio de las muestras y es
independiente de las amplitudes de los intervalos. Se simboliza como Ẋ y se
encuentra sólo para variables cuantitativas.
Se encuentra sumando todos los valores y dividiendo por el número total de datos,
también podemos calcular con las siguientes fórmulas dependiendo según sea la
serie.
1.
∑𝑥
2.
𝑁
∑𝑓𝑥
𝑁
3.
∑𝑓.𝑥𝑖
𝑁
En una serie simple (donde no se repiten los valores) el promedio su cálculo con la
fórmula 1, en caso de serie de frecuencias (con valores repetidos) el promedio se
calcula con la fórmula 2 y si, se trata de una serie agrupada (en intervalos de
amplitud constante) el promedio se calcula con la fórmula 3.
Lo que significa cada fórmula.
Fórmula 1
∑𝑥
𝑁
= suma de todos los valores dividido entre el número (N) de valores.
∑𝑓𝑥
Fórmula 2 𝑁 = sumatoria de los productos de las frecuencias (f) por los valores
(x), dividido entre el número (N) de casos.
∑𝑓.𝑥𝑖
En 3: 𝑁 = suma de los productos de las marcas de clase (Xi) por las frecuencias
(f) de cada intervalo, dividido entre el número (N) de casos.
En este caso usaremos la fórmula tres debido, a que se trata de una serie agrupada
(en intervalos de amplitud constante).
Datos a trabajar: En un salón de clases del Instituto Básico por Cooperativa “IBU”
de tercero básico sección “A”, luego de una unidad didáctica se obtuvieron los
siguientes resultados de la evaluación de Comunicación y Lenguaje
93,56,86,96,70,73,86,94,93,98,48,87,91,41,84,90,92,74,85,83,91,96,86,87,92,85,9
3,68,89
Pasos a seguir:
1) contar la serie de datos o valores (N). En este caso (N) = 29
2) Ordenar de manera ascendente y representar el valor mínimo (Xi) y valor
máximo (Xs).
41,48,56,68,70,73,74,83,84,85,85,86,86,86,87,87,89,90,91,91,92,92,93,93,93,94,9
6,96,98
Valor mínimo (Xi) = 41
Valor máximo (Xs) = 98
𝐑
3) Para calcular la amplitud de intervalos aplicaremos la fórmula 𝐢 = 𝐊 .
Donde:
R es el rango.
K son los números de intervalos de clases.
Rango (R): es la diferencia entre el valor mínimo y máximo, para calcular se usa
la siguiente fórmula. R = Xs − Xi
Números de intervalos de clases (k): Es el valor que representa a un
intervalo de clase y para calcular se usa la siguiente fórmula. K = 1 +
3.33 log(N)
R= Xs-Xi
R= 98-41
R= 57
K=1+3.3log(n)
K= 1+3.3log(30)
K= 2.95
K= 3
i=R/K
i=57/3
i= 19
La amplitud de cada intervalo será de 12
1) Elaborar una tabla y tabular los intervalos según lo calculado. Para empezar a
tabular tener en cuenta los números de casos y la amplitud, ambas fueron
calculadas.
1.1 Intervalo de clases (f)
Para el primer intervalo se inicia con el valor mínimo de la serie (41) luego se
empieza a contar 12 unidades (resultado del cálculo de amplitud) incluyendo el valor
mínimo. También se puede tabular de la siguiente manera: sumar el resultado de la
amplitud al valor mínimo y restarle uno.
El primer intervalo queda de la siguiente manera (41 + 12) = 53, quiere decir que el
primer intervalo comienza desde 41 hasta 53; para el segundo intervalo se comienza
desde el 54.
Para segundo intervalo se vuelve hacer igual que la primera sumar el resultado de
la amplitud al valor que continua y restarle uno. El segundo intervalo queda de la
siguiente manera (53 + 12) = 65; quiere decir que el segundo intervalo comienza
desde 65 termina hasta 77; así sucesivamente hasta alcanzar el valor máximo.
1.2 Frecuencia (f).
Para la frecuencia se cuentan los valores que hay en cada intervalo. Se cuentan los
valores que esta desde 41 al 53; igual pasa con el segundo intervalo, se cuentan
los valores que esta desde 54 al 65. Así sucesivamente hasta completar la tabla.
1.3 marca de clase (Xi).
Es el punto medio o promedio de cada intervalos
maraca
intervalo. La marca de clase es el valor que de clases frecuencia de clase
(f)
representa a todo el intervalo para el cálculo de
(i)
(xi)
algunos parámetros como la media aritmética o 41 – 60
3
69.5
la desviación típica. Se calcula a través de la
4
88.5
60 – 79
Li+Ls
siguiente fórmula Xi = 2 ; significa marca de
22
107.5
79 – 98
clase es igual a límite inferior más límite
∑f 29
superior dividido entre dos. Para la marca de
79+84
clase del primer intervalo calcularemos de la siguiente manera
Xi = 2 = 81.5;
para la segunda marca de clase es más fácil sumarle 6 (resultado del cálculo de
amplitud) del resultado del primer intervalo que es 81.5, quedaría 81.5 + 6 = 87.5
El resultado se vuelve a sumarle 6 para el tercer intervalo y así sucesivamente
hasta completar la tabla
Como medida de control y para posteriores cálculos en el tabular se coloca la
columna Fa- (frecuencia acumulada ó menos) que se obtiene de sumar
sucesivamente las frecuencias absolutas de los intervalos (f) y para calcular la
Media aritmética se agrega la columna para hacer mc.f (marca de clase por
frecuencias)
Tabla de distribución de frecuencias
intervalos
frecuencia maraca
frecuencia
de
acumulada de clase
(f)
(fa)
(xi)
clases (i)
3
69.5
41 – 60
3
4
88.5
4
60 – 79
22
107.5
79 – 98
22
(f.xi)
208.5
354
2,365
fr
%f
0.1034
0.1379
0.7586
10.34
13.79
75.86
100%
∑f 29
2. habiendo hecho el tabular y elaborada la columna ∑f. xi 2,927.5, se procede a
calcular la media aritmética:
∑f. xi
2,927.5
=
= 97.58%
N
30
R//. Entonces la Media Aritmética es 97.58%:
En este resultado el porcentaje % indica que el grupo evaluado ha tenido un logro
equivalente a 97.58% lo cual indica que se tuvo una pérdida del 2.42 %.
6. La mediana (Md). Es el valor de la variable que ocupa el lugar central
si tenemos un número impar de datos. En caso contrario la mediana
coincide con la media aritmética de los valores centrales. La mediana
tiene la propiedad de que el 50% de los datos son menores o iguales
que ella y el otro 50% son mayores o iguales. Entonces la mediana
divide el conjunto de datos en dos subconjuntos iguales.
Md = 87
7. La moda (Mo). La moda es el valor de la variable con mayor frecuencia. Si los
datos los tenemos agrupados en clases la llamamos clase modal.
Mo = 86.93
Cuando se obtiene una serie de datos no basta con hacer cálculos, se recomienda
hacer una gráfica en la cual ya se pueden interpretar las características del grupo,
tales como: amplitud de la serie, valor máximo, valor, mínimo, ubicación de los
promedios (media, mediana, moda), cual tiene mayor frecuencia (Mo), cual tiene
menos frecuencia, la cantidad de valores.
7.3 Polígono de frecuencias
Es una gráfica que permite la rápida visualización de las frecuencias de cada
una de las categorías del estudio. Normalmente su utiliza con frecuencias
absolutas.
Dentro de la gráfica en el eje (horizontal) se colocan los valores o marcas de
clase y en el eje “y” (vertical) se colocan las frecuencias.
Calificaciones de las alumnos de Tercero Básico
Seccion "A"
25
107,5; 22
frecuencias
20
15
10
5
69,5; 3
88,5; 4
0; 1
0
0
20
40
60
80
Marca de clase de datos agrupados
100
120
INTERPRETACIÓN FINAL DEL POLIGONO DE FRECUENCIA
En esta gráfica podemos encontrar los datos y resultados alcanzados en el grupo
de estudiantes de Tercero Básico Sección “A” del Instituto Básico por Cooperativa
IBU”, los datos de las notas de los estudiantes están representados por medio de
un polígono de frecuencias, que facilita comprender las calificaciones obtenidas por
los estudiantes, con quienes realicé la práctica Docente.
Podemos ver que las calificaciones que se obtuvieron en este proceso de práctica
Docente, van desde 41 a 98 puntos; el cual refleja un alto grado de satisfacción
debido a que la mayoría de estudiantes los estudiantes de esa sección tiene una
ponderación superiores a 60 puntos, que es el punteo mínimo para la aprobación
del curso. Los datos obtenidos reflejan que el 98% de los estudiantes aprobaron
satisfactoriamente el grado de tercero básico.