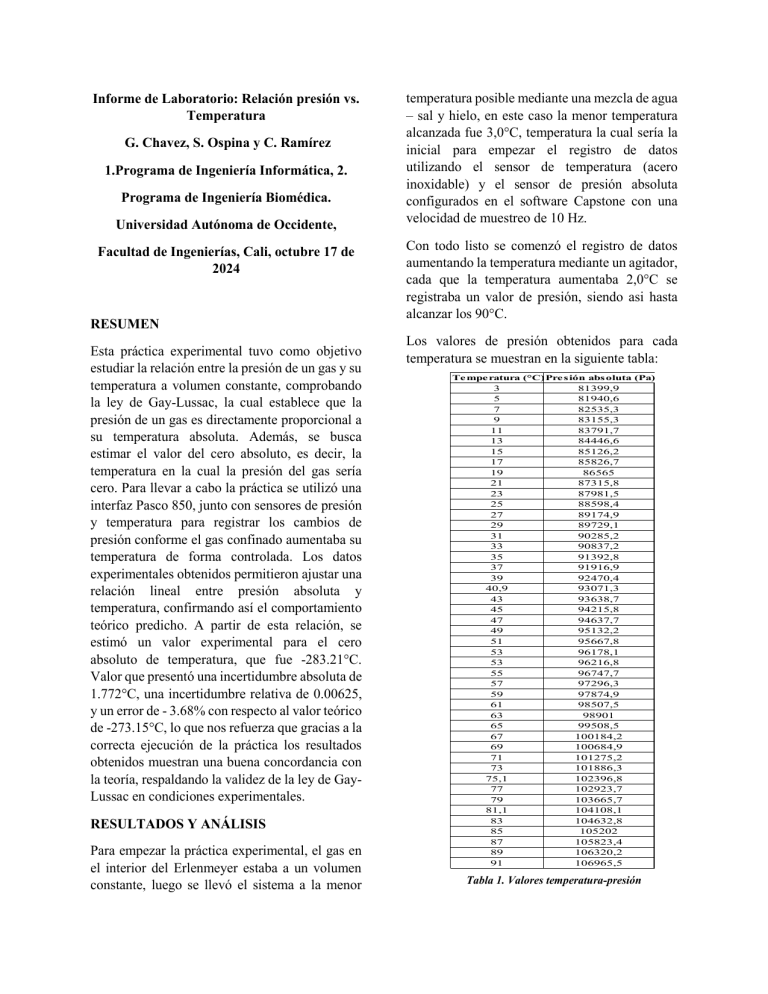
Informe de Laboratorio: Relación presión vs. Temperatura G. Chavez, S. Ospina y C. Ramírez 1.Programa de Ingeniería Informática, 2. Programa de Ingeniería Biomédica. Universidad Autónoma de Occidente, Facultad de Ingenierías, Cali, octubre 17 de 2024 RESUMEN Esta práctica experimental tuvo como objetivo estudiar la relación entre la presión de un gas y su temperatura a volumen constante, comprobando la ley de Gay-Lussac, la cual establece que la presión de un gas es directamente proporcional a su temperatura absoluta. Además, se busca estimar el valor del cero absoluto, es decir, la temperatura en la cual la presión del gas sería cero. Para llevar a cabo la práctica se utilizó una interfaz Pasco 850, junto con sensores de presión y temperatura para registrar los cambios de presión conforme el gas confinado aumentaba su temperatura de forma controlada. Los datos experimentales obtenidos permitieron ajustar una relación lineal entre presión absoluta y temperatura, confirmando así el comportamiento teórico predicho. A partir de esta relación, se estimó un valor experimental para el cero absoluto de temperatura, que fue -283.21°C. Valor que presentó una incertidumbre absoluta de 1.772°C, una incertidumbre relativa de 0.00625, y un error de - 3.68% con respecto al valor teórico de -273.15°C, lo que nos refuerza que gracias a la correcta ejecución de la práctica los resultados obtenidos muestran una buena concordancia con la teoría, respaldando la validez de la ley de GayLussac en condiciones experimentales. RESULTADOS Y ANÁLISIS Para empezar la práctica experimental, el gas en el interior del Erlenmeyer estaba a un volumen constante, luego se llevó el sistema a la menor temperatura posible mediante una mezcla de agua – sal y hielo, en este caso la menor temperatura alcanzada fue 3,0°C, temperatura la cual sería la inicial para empezar el registro de datos utilizando el sensor de temperatura (acero inoxidable) y el sensor de presión absoluta configurados en el software Capstone con una velocidad de muestreo de 10 Hz. Con todo listo se comenzó el registro de datos aumentando la temperatura mediante un agitador, cada que la temperatura aumentaba 2,0°C se registraba un valor de presión, siendo asi hasta alcanzar los 90°C. Los valores de presión obtenidos para cada temperatura se muestran en la siguiente tabla: Te mpe ratura (°C) Pre s ión abs oluta (Pa) 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33 35 37 39 40,9 43 45 47 49 51 53 53 55 57 59 61 63 65 67 69 71 73 75,1 77 79 81,1 83 85 87 89 91 81399,9 81940,6 82535,3 83155,3 83791,7 84446,6 85126,2 85826,7 86565 87315,8 87981,5 88598,4 89174,9 89729,1 90285,2 90837,2 91392,8 91916,9 92470,4 93071,3 93638,7 94215,8 94637,7 95132,2 95667,8 96178,1 96216,8 96747,7 97296,3 97874,9 98507,5 98901 99508,5 100184,2 100684,9 101275,2 101886,3 102396,8 102923,7 103665,7 104108,1 104632,8 105202 105823,4 106320,2 106965,5 Tabla 1. Valores temperatura-presión Sustituyendo, nos queda la siguiente ecuación. Al llevar estos datos a graficar se evidencia la relación lineal coherente con la ley de GayLussac, lo que demuestra esa directa proporcionalidad entre la presión y la temperatura que la formula de la ley de Gay-Lussac (P = αT) ilustra. 𝑇(°𝐶) = 𝑉 𝑃 − 273.15 𝑛𝑅 La ecuación muestra cómo se calcula la temperatura en grados Celsius relacionando la presión, el volumen, la cantidad de gas y la constante de los gases ideales. Además, el papel del término −273.15 ajusta la temperatura a la escala Celsius, ya que el cero absoluto en Kelvin equivale a −273.15 °C. Una vez teniendo esta ecuación podemos relacionar la ecuación arrojada por la gráfica, donde la pendiente nos da el valor constante que depende del numero de moles, volumen y constante de los gases ideales, y el intercepto (b) el valor de la presion a una temperatura de 0 °C. 𝑃 = 𝑝𝑒𝑛𝑑𝑇 + 𝑏 Donde: Grafica 1. Presión Absoluta (Pa) Vs Temperatura (°C) 𝑝𝑒𝑛𝑑 = Por otra parte, para relacionar la ecuación lineal que la gráfica nos genera partimos de la ecuación de estado de los gases ideales. 𝑃𝑉 = 𝑛𝑅𝑇 Al despejar la temperatura T de esta ecuación, logramos hallar la temperatura en grados Kelvin, viendo como se relaciona con la presion, volumen, número de moles y la constante de los gases ideales. 𝑇𝑘 = 𝑃𝑉 𝑛𝑅 Teniendo esto, necesitamos la relación entre la temperatura en grados Kelvin y grados Celsius la cual es la siguiente. Extrapolando los datos experimentales a la temperatura en la que la presion seria cero, se obtuvo el siguiente calculo para obtener la temperatura del cero absoluto. 𝑃=0 𝑃 = 𝑝𝑒𝑛𝑑𝑇 + 𝑏 Seguido a esto despejamos el valor de la temperatura del cero absoluto. 𝑇𝑐 = −𝑏 𝑝𝑒𝑛𝑑 Sustituyendo valores nos arroja el siguiente resultado: 𝑇𝑐 = 𝑇(°𝐶) = 𝑇𝑘 − 273.15 𝑉 𝑛𝑅 −81000 = −283.21°𝐶 286 CONCLUSIONES ∆𝑇𝑐 = | 𝜕𝑇𝑐 𝜕𝑇𝑐 ∙ ∆𝑏| + | ∙ ∆𝑝𝑒𝑛𝑑| 𝜕𝑏 𝜕𝑝𝑒𝑛𝑑 −1 𝑏 𝛥𝑇𝑐 = | ⋅ 𝛥𝑏| + | ⋅ 𝛥𝑝𝑒𝑛𝑑| 𝑝𝑒𝑛𝑑 𝑝𝑒𝑛𝑑 2 −1 81000 𝛥𝑇𝑐 = | ⋅ 82| + | ⋅ 1,5| 286 2862 ∆𝑇𝑐 ≈ ±1.772°𝐶 ∆𝑇𝑐 1.772°𝐶 = ≈ 0.00625 𝑇𝑐 283.21°𝐶 %𝐸𝑅 = | − 273.15°𝐶 − (−283.21°𝐶) | ∙ 100 −273.15°𝐶 %𝐸𝑅 ≈ − 3.68% Teniendo en cuenta los resultados obtenidos podemos observar que el valor del cero absoluto obtenido experimentalmente corresponde a −283.21°𝐶 lo que representa una desviación de 0.00625 con respecto al valor teórico del cero absoluto −273.15°𝐶. Además, es posible evidenciar margen de error del −3.68%, valor aceptable que puede tener diferentes causas, como la eficiencia misma de los sensores y que el sistema no se encontrase en un equilibrio térmico pleno antes de comenzar el registro de datos. Mediante la práctica experimental se logró verificar con éxito la ley de Gay-Lussac, demostrando que la presión de un gas aumenta proporcionalmente con su temperatura cuando el volumen se mantiene constante. Los datos experimentales recopilados confirmaron esta relación, y el ajuste lineal de los mismos arrojó una pendiente de 286 𝑃𝑎 y una intersección de °𝐶 81,000 Pa. Estos valores son coherentes con el comportamiento teórico esperado según la ley de los gases ideales, que establece una relación directa entre la presión y la temperatura de un gas bajo estas condiciones. Además, al extrapolar los datos, se obtuvo un valor para el cero absoluto de -283.21 °C, que está relativamente cerca del valor teórico de -273.15 °C, con un error del -3.68%. Diferencia que puede atribuirse a diversas fuentes de error, como la precisión limitada de los sensores de presión y temperatura, pequeñas fluctuaciones térmicas durante el experimento y las desviaciones del comportamiento del gas ya que en la práctica un gas no tiene un comportamiento ideal, y esto puede ser más notable a bajas temperaturas y altas presiones. A pesar de estas posibles fuentes de error, el experimento si consiguió mostrar una clara coherencia con la teoría de los gases ideales y validando la ley de Gay-Lussac experimentalmente. Los resultados obtenidos proporcionan una representación precisa de cómo la presión de un gas responde a los cambios de temperatura, subrayando la importancia de este principio en el estudio del comportamiento de los gases.