UNI - Facultad de Ingeniería Química y Textil / Matemática Básica

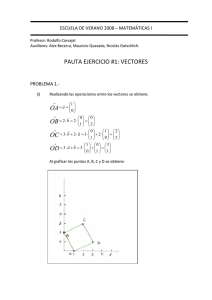
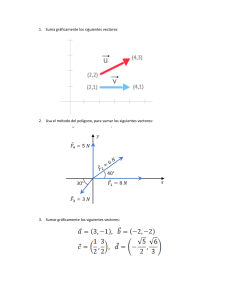
Semana 5:
1. Valores y Vectores propios.
Sea 𝐴 ∈ 𝑀𝑎𝑡𝑛𝑥𝑛 (ℝ), 𝑣̅𝑖 ∈ 𝑀𝑎𝑡𝑛𝑥1 (ℝ) y 𝜆𝑖 ∈ ℝ, con 𝑣̅𝑖 ≠ 0̅.
Se dice que 𝑣̅𝑖 y 𝜆𝑖 son vector y valor propio de A respectivamente, si cumplen la
siguiente relación:
𝐴𝑣̅𝑖 = 𝜆𝑖 𝑣̅𝑖 … (1)
De manera equivalente:
𝐴𝑇 𝑣̅𝑖 = 𝜆𝑖 𝑣̅𝑖 → 𝜆𝑖 𝑣̅𝑖 − 𝐴𝑇 𝑣̅𝑖 = 0̅ → (𝜆𝑖 𝐼𝑛 − 𝐴𝑇 )𝑣̅𝑖 = 0̅
Entonces:
(𝜆𝑖 𝐼𝑛 − 𝐴𝑇 )𝑣̅𝑖 = 0̅ … (2)
Aplicación directa de (1):
𝐴(𝐴𝑣̅𝑖 ) = 𝐴(𝜆𝑖 𝑣̅𝑖 ) → 𝐴2 𝑣̅𝑖 = 𝜆𝑖 𝐴𝑣̅𝑖 → 𝐴2 𝑣̅𝑖 = 𝜆𝑖 (𝜆𝑖 𝑣̅𝑖 ) → 𝐴2 𝑣̅𝑖 = 𝜆𝑖 2 𝑣̅𝑖
Y en general:
𝐴𝑛 𝑣̅𝑖 = 𝜆𝑖 𝑛 𝑣̅𝑖 … (3)
Cuestión 1: ¿Cómo determino los valores y vectores propios de una matriz?
2. Polinomio característico de una transformación Lineal, Propiedades.
Sea 𝐴𝑇 ∈ 𝑀𝑎𝑡𝑛𝑥𝑛 (ℝ) la matriz asociada a una transformación Lineal “T”, por la
ecuación (2) se cumple:
(𝜆𝑖 𝐼𝑛 − 𝐴𝑇 )𝑣̅𝑖 = 0̅ → |𝜆𝑖 𝐼𝑛 − 𝐴𝑇 ||𝑣̅𝑖 | = 0
Dado que 𝑣̅𝑖 ≠ 0̅:
|𝜆𝑖 𝐼𝑛 − 𝐴𝑇 | = 0 … (4)
El polinomio característico de 𝐴𝑇 se define como:
𝑃𝑛 (𝜆) = |𝜆𝐼𝑛 − 𝐴𝑇 |
Entonces para obtener los valores propios de 𝐴𝑇 se hallan las raíces de 𝑃𝑛 (𝜆) y
posteriormente se reemplaza en la ecuación (2) para hallar los vectores propios.
Ejemplo 1:
Dado 𝐴𝑇 ∈ 𝑀𝑎𝑡2𝑥2 (ℝ), hallar el polinomio característico, los valores y vectores
propios.
𝐴𝑇 = [
5 3
]
2 4
Hallando el polinomio característico:
1 0
5 3
𝑃2 (𝜆) = |𝜆 [
]−[
]|
0 1
2 4
𝜆 − 5 −3
𝑃2 (𝜆) = |
|
−2 𝜆 − 4
𝑃2 (𝜆) = (𝜆 − 5)(𝜆 − 4) − (−2)(−3)
𝑃2 (𝜆) = 𝜆2 − 4𝜆 − 5𝜆 + 20 − 6
𝑃2 (𝜆) = 𝜆2 − 9𝜆 + 14
𝑃2 (𝜆) = (𝜆 − 2)(𝜆 − 7)
Encontrando los valores propios:
𝑃2 (𝜆𝑖 ) = 0
(𝜆𝑖 − 2)(𝜆𝑖 − 7) = 0
𝜆1 = 2, 𝜆2 = 7
Encontrando los vectores propios reemplazando en (2):
•
Para 𝜆1 = 2:
(2 [
1 0
5
]−[
0 1
2
3
]) 𝑣̅1 = 0̅
4
𝑓1 𝑓2
−3 −3
1
1
] 𝑣̅1 = 0̅ → − 𝑦
→[
] 𝑣̅ = 0̅ ~
−2 −2
−1 −1 1
3
2
1 1 𝑥
1
1
[
] 𝑣̅1 = 0̅ → 𝑓2 + 𝑓1 → [
] ( ) = 0̅ ~
0 0 𝑦
−1 −1
1 1 𝑥
[
] ( ) = 0̅ → 𝑥 + 𝑦 = 0 → 𝑦 = −𝑥 ~
0 0 𝑦
[
𝑥
1
) , 𝑥 = 1 → 𝑣̅1 = ( )
−𝑥
−1
𝑣̅1 = (
•
Para 𝜆2 = 7:
1 0
5 3
(7 [
]−[
]) 𝑣̅2 = 0̅
0 1
2 4
2 −3
2 −3 𝑥
[
] 𝑣̅2 = 0̅ → 𝑓2 + 𝑓1 → [
] ( ) = 0̅ ~
−2 3
0 0 𝑦
2
2 −3 𝑥
[
] (𝑦) = 0̅ → 2𝑥 − 3𝑦 = 0 → 𝑦 = 𝑥 ~
0 0
3
𝑥
3
𝑣̅1 = (2 𝑥 ) , 𝑥 = 3 → 𝑣̅1 = ( )
2
3
Cuestión 2: ¿La matriz 𝐴𝑇 ∈ 𝑀𝑎𝑡𝑛𝑥𝑛 (ℝ) tendrá siempre “n” valores y vectores
propios distintos?
Observaciones:
-
-
Por las definiciones dadas previamente queda claro que a cada valor
propio le corresponde al menos un vector propio.
Al ser 𝑃𝑛 (𝜆) un polinomio de grado “n”, por el teorema fundamental del
álgebra, tiene “n” raíces no necesariamente distintas. Entonces no siempre
se tendrán “n” valores propios distintos.
Por tanto, tampoco tendrá siempre “n” vectores propios distintos.
Cada 𝜆𝑖 tiene asociado subespacio vectorial generado por sus 𝑣̅𝑖
asociados.
Definiciones:
-
Multiplicidad Algebraica (MA): Es el número de veces que el valor propio
aparece en 𝑃𝑛 (𝜆) como raíz.
Multiplicidad Geométrica (MG): Es el número de vectores propios distintos
que genera el valor propio.
Teorema: 𝑀𝐺𝑖 ≤ 𝑀𝐴𝑖
Ejemplo 2:
Dado 𝐴𝑇 ∈ 𝑀𝑎𝑡2𝑥2 (ℝ), hallar el polinomio característico, los valores y vectores
propios.
𝐴𝑇 = [
−2 −1
]
1
0
Hallando el polinomio característico:
1 0
−2 −1
]−[
]|
0 1
1
0
𝜆+2 1
𝑃2 (𝜆) = |
|
−1 𝜆
𝑃2 (𝜆) = |𝜆 [
𝑃2 (𝜆) = (𝜆 + 2)𝜆 − (−1)1
𝑃2 (𝜆) = 𝜆2 + 2𝜆 + 1
𝑃2 (𝜆) = (𝜆 + 1)2
Encontrando los valores propios:
𝑃2 (𝜆𝑖 ) = 0
(𝜆𝑖 + 1)2 = 0
𝜆1 = −1 (𝑀𝐴1 = 2)
Encontrado los vectores propios reemplazando en (2):
•
Para 𝜆1 = −1:
1
(−1 [
0
0
−2 −1
]−[
]) 𝑣̅1 = 0̅
1
1
0
1 1
1
1
[
] 𝑣̅1 = 0̅ → 𝑓2 + 𝑓1 → [
] 𝑣̅ = 0̅ ~
0 0 1
−1 −1
1 1 𝑥
[
] ( ) = 0̅ → 𝑥 + 𝑦 = 0 → 𝑦 = −𝑥 ~
0 0 𝑦
𝑥
1
) , 𝑥 = 1 → 𝑣̅1 = ( ) (𝑀𝐺1 = 1)
−𝑥
−1
𝑣̅1 = (
Se verifica: 𝑀𝐺1 ≤ 𝑀𝐴1
𝑃𝑛 (𝜆) cumple las siguientes propiedades:
-
Sus raíces son los autovalores de 𝐴𝑇
𝑃𝑛 (𝜆𝑖 ) = 0
-
𝑃𝑛 (𝜆) es mónico: Coeficiente principal igual a 1.
El coeficiente “n-1”-ésimo es “−𝑇𝑟(𝐴𝑇 )”
𝑇𝑟(𝐴𝑇 ) = ∑ 𝑀𝐴𝑖 𝜆𝑖
𝑖
-
Su término independiente es “(−1)𝑛 |𝐴𝑇 |”
𝑃𝑛 (0) = |−𝐴𝑇 | = (−1)𝑛 |𝐴𝑇 |
|𝐴𝑇 | = ∏ 𝜆𝑖 𝑀𝐴𝑖
𝑖
Semana 6:
3. Semejanza de matrices.
Definición: Sea 𝐴, 𝐵 ∈ 𝑀𝑎𝑡𝑛𝑥𝑛 (ℝ), son semejantes si:
∃𝑃, 𝑃−1 ∈ 𝑀𝑎𝑡𝑛𝑥𝑛 (ℝ) | 𝑃𝐵 = 𝐴𝑃 ↔ 𝐵 = 𝑃−1 𝐴𝑃
Teorema: Si 𝐴, 𝐵 ∈ 𝑀𝑎𝑡𝑛𝑥𝑛 (ℝ) son semejantes, entonces sus polinomios
característicos son iguales:
|𝜆𝐼𝑛 − 𝐴| = |𝜆𝐼𝑛 − 𝐵|
Demostración:
|𝜆𝐼𝑛 − 𝐴| = |𝜆𝑃 −1 𝑃 − 𝑃−1 𝐵𝑃| = |𝑃−1 (𝜆𝐼𝑛 − 𝐵)𝑃| =
1
|𝜆𝐼 − 𝐵||𝑃| = |𝜆𝐼𝑛 − 𝐵|
|𝑃| 𝑛
4. Diagonalización de Matrices.
Definición: Sea 𝐴 ∈ 𝑀𝑎𝑡𝑛𝑥𝑛 (ℝ), es diagonalizable si ∃𝐷 ∈ 𝑀𝑎𝑡𝑛𝑥𝑛 (ℝ) diagonal, tal
que A y D son semejantes.
Sea 𝐴 ∈ 𝑀𝑎𝑡𝑛𝑥𝑛 (ℝ) una matriz diagonalizable, para diagonalizarla se pueden
seguir los siguientes pasos:
-
Hallar el polinomio característico de A (𝑃𝑛 (𝜆))
Encontrar los valores propios (𝑃𝑛 (𝜆𝑖 ) = 0)
Encontrar los vectores propios ((𝜆𝑖 𝐼𝑛 − 𝐴𝑇 )𝑣̅𝑖 = 0̅)
Construir 𝑃 (𝑃 = [𝑣̅1 ⋯ 𝑣̅𝑛 ])
Hallar 𝑃−1 ((𝑃|𝐼𝑛 )~(𝐼𝑛 |𝑃 −1))
Calcular D (𝐷 = 𝑃−1 𝐴𝑃)
Ejemplo 3:
Siguiendo con el Ejemplo 1, tenemos:
𝐴𝑇 = [
5 3
]
2 4
𝑃2 (𝜆) = (𝜆 − 2)(𝜆 − 7)
𝜆1 = 2, 𝜆2 = 7
•
•
1
Para 𝜆1 = 2 → 𝑣1 = ( )
−1
3
Para 𝜆2 = 7 → 𝑣̅2 = ( )
2
Construyendo P:
1 3
𝑃=[
]
−1 2
Hallando 𝑃−1:
𝑓2
31 0
1 31 0
|
)→ →(
|1 1 ) ~
51 1
0 15 5
5
2
3
0
1 0 5 −5
) = (𝐼𝑛 |𝑃 −1 )
1) → 𝑓1 − 3𝑓2 → (
|
1 1
0
1
5
5 5
1
1 31 0
|
) → 𝑓2 + 𝑓1 → (
0
−1 2 0 1
(
(
1 31
|1
0 15
2
3
−
5]
∴ 𝑃−1 = [5
1 1
5 5
Calculando D:
2
3
−
5] [5
𝐷 = 𝑃 −1 𝐴𝑃 = [5
1 1 2
5 5
Observaciones:
4
6
−
3
5] [ 1 3] = [2 0]
] 𝑃 = [5
7
7
0 7
−1 2
4
5 5
-
-
𝐴𝑇 es diagonalizable si y solo si para todo valor propio de 𝐴𝑇 (𝜆𝑖 ) se cumple
𝑀𝐴𝑖 = 𝑀𝐺𝑖
𝜆1 ⋯ 0
La matriz diagonalizada de 𝐴𝑇 tiene la forma 𝐷 = [ ⋮ ⋱ ⋮ ]
0 ⋯ 𝜆𝑛
Si 𝐴𝑇 es simétrica, siempre es diagonalizable.
Semana 7:
5. Diagonalización Ortogonal (Base ortonormal).
Definición: Los vectores unitarios 𝑥̂1 , … , 𝑥̂𝑛 , forman una base ortonormal si son
linealmente independientes y ortogonales entre sí, es decir:
|𝑥̂𝑖 | = 1, ∀ 𝑖
𝑛
∑ 𝑎𝑖 𝑥̂𝑖 = 0 ↔ 𝑎𝑖 = 0, ∀𝑥̂𝑖 , 𝑖
𝑖=1
𝑥̂𝑖 ∙ 𝑥̂𝑗 = 0, ∀𝑖 ≠ 𝑗
Definición: Sea 𝐴 ∈ 𝑀𝑎𝑡𝑛𝑥𝑛 (ℝ), es diagonalizable ortogonalmente si ∃𝐷 ∈
𝑀𝑎𝑡𝑛𝑥𝑛 (ℝ) diagonal y ∃𝑄 ∈ 𝑀𝑎𝑡𝑛𝑥𝑛 (ℝ) ortogonal (𝑄 −1 = 𝑄 𝑇 ) tal que:
𝐷 = 𝑄 −1 𝐴𝑄 = 𝑄 𝑇 𝐴𝑄
Además 𝐴𝑇 es diagonalizable ortogonalmente si y solo si A es simétrica.
Sea 𝑥̂1 , … , 𝑥̂𝑛 una base ortornormal de vectores propios de A asociados a los
valores propios 𝜆1 , … , 𝜆𝑛 , se construye Q de la siguiente manera:
𝑄 = [𝑥̂1
⋯
𝑥̂𝑛 ]
Observaciones:
-
Si 𝐴𝑇 es simétrica, los subespacios vectoriales generados por valores
propios 𝜆𝑖 distintos son ortogonales entre sí.
Si 𝐴𝑇 es simétrica y tiene “n” valores propios distintos, entonces 𝑣̂1 , … , 𝑣̂𝑛
(vectores unitarios de los vectores propios) forman una base ortonormal,
entonces:
𝑄 = [𝑣̂1
⋯
𝑣̂𝑛 ]
Ejemplo 4:
Dado 𝐴𝑇 ∈ 𝑀𝑎𝑡2𝑥2 (ℝ), hallar el polinomio característico, los valores, vectores
propios y la matriz ortonormal “Q”.
1
𝐴𝑇 = [
2
2
]
−2
Hallando el polinomio característico:
1 0
1 2
𝑃2 (𝜆) = |𝜆 [
]−[
]|
0 1
2 −2
𝜆 − 1 −2
𝑃2 (𝜆) = |
|
−2 𝜆 + 2
𝑃2 (𝜆) = (𝜆 − 1)(𝜆 + 2) − (−2)(−2)
𝑃2 (𝜆) = 𝜆2 + 2𝜆 − 𝜆 − 2 − 4
𝑃2 (𝜆) = 𝜆2 + 𝜆 − 6
𝑃2 (𝜆) = (𝜆 + 3)(𝜆 − 2)
Encontrando los valores propios:
𝑃2 (𝜆𝑖 ) = 0
(𝜆𝑖 + 3)(𝜆𝑖 − 2) = 0
𝜆1 = −3, 𝜆2 = 2
Encontrando los vectores propios reemplazando en (2):
•
Para 𝜆1 = −3:
(−3 [
1 0
1
]−[
0 1
2
2
]) 𝑣̅1 = 0̅
−2
𝑓1
−4 −2
2
1
[
] 𝑣̅1 = 0̅ → − → [
] 𝑣̅ = 0̅ ~
−2 −1
−2 −1 1
2
2 1 𝑥
2
1
[
] 𝑣̅1 = 0̅ → 𝑓2 + 𝑓1 → [
] ( ) = 0̅ ~
0 0 𝑦
−2 −1
2 1 𝑥
[
] ( ) = 0̅ → 2𝑥 + 𝑦 = 0 → 𝑦 = −2𝑥 ~
0 0 𝑦
1
𝑥
1
) , 𝑥 = 1 → 𝑣̅1 = ( ) → 𝑣̂1 =
−2𝑥
−2
𝑣̅1 = (
•
√5
2
−
( √5)
Para 𝜆2 = 2:
1 0
1 2
(2 [
]−[
]) 𝑣̅2 = 0̅
0 1
2 −2
𝑓2
1 −2
1 −2
[
] 𝑣̅2 = 0̅ →
→[
] 𝑣̅ = 0̅ ~
−2 4
−1 2 2
2
1 −2 𝑥
1 −2
[
] 𝑣̅2 = 0̅ → 𝑓2 + 𝑓1 → [
] ( ) = 0̅ ~
0 0 𝑦
−1 2
𝑥
1 −2 𝑥
[
] (𝑦) = 0̅ → 𝑥 − 2𝑦 = 0 → 𝑦 = ~
0 0
2
𝑥
2
𝑣̅2 = (𝑥) , 𝑥 = 2 → 𝑣̅2 = ( ) → 𝑣̂2 =
1
2
2
√5
1
(√5)
Verificando:
1
𝑣̂1 ∙ 𝑣̂2 =
2
√5 ∙ √5 = 0
2
1
−
( √5) (√5)
Construyendo Q:
1
𝑄=
2
√5 √5
2
1
−
[ √5 √5]
Cuestión 3: ¿Cómo hallamos la matriz Q si se tiene menos de “n” valores propios
distintos?
6. Proceso de Ortogonalización de Gram-Schmidt
Sean 𝑣̅1 , … , 𝑣̅𝑛 una base del espacio vectorial V, y sean 𝑥̅1 , … , 𝑥̅𝑛 una base
ortogonal de V, se definen como:
𝑥̅1 = 𝑣̅1
𝑘−1
𝑥̅𝑘 = 𝑣̅𝑘 − ∑ 𝑃𝑟𝑜𝑦𝑥̅𝑗 (𝑣̅𝑘 )
𝑗=1
Donde:
𝑃𝑟𝑜𝑦𝑥̅ 𝑗 (𝑣̅𝑘 ) =
𝑣̅𝑘 ∙ 𝑥̅𝑗
|𝑥̅𝑗 |
∙
𝑥̅𝑗
|𝑥̅𝑗 |
=
𝑣̅𝑘 ∙ 𝑥̅𝑗
|𝑥̅𝑗 |
2
∙ 𝑥̅𝑗
Ejemplo 5:
Dado 𝐴𝑇 ∈ 𝑀𝑎𝑡3𝑥3 (ℝ), hallar el polinomio característico, los valores, vectores
propios y la matriz ortonormal “Q”.
2 1
𝐴 𝑇 = [1 2
1 1
1
1]
2
Hallando el polinomio característico:
1 0 0
2 1 1
𝑃3 (𝜆) = |𝜆 [0 1 0] − [1 2 1]|
0 0 1
1 1 2
𝜆 − 2 −1
−1
𝑃3 (𝜆) = | −1 𝜆 − 2 −1 |
−1
−1 𝜆 − 2
𝑃3 (𝜆) = (𝜆 − 2)3 − 1 − 1 − (𝜆 − 2) − (𝜆 − 2) − (𝜆 − 2)
𝑃3 (𝜆) = (𝜆 − 1 − 1)3 − 2 − 3(𝜆 − 1 − 1)
𝑃3 (𝜆) = (𝜆 − 1)3 − 3(𝜆 − 1)2 + 3(𝜆 − 1) − 1 − 2 − 3(𝜆 − 1) + 3
𝑃3 (𝜆) = (𝜆 − 1)3 − 3(𝜆 − 1)2
𝑃3 (𝜆) = (𝜆 − 1)2 (𝜆 − 1 − 3)
𝑃3 (𝜆) = (𝜆 − 1)2 (𝜆 − 4)
Encontrando los valores propios:
𝑃3 (𝜆𝑖 ) = 0
(𝜆𝑖 − 1)2 (𝜆𝑖 − 4) = 0
𝜆1 = 1 (𝑀𝐴1 = 2), 𝜆2 = 4
Encontrando los vectores propios reemplazando en (2):
•
Para 𝜆1 = 1 (𝑀𝐴1 = 2):
1 0
([0 1
0 0
−1
[−1
−1
−1
[0
0
−1
−1
−1
−1
0
0
0
2 1
0] − [1 2
1
1 1
1
1]) 𝑣̅1,2 = 0̅
2
−1
−1 −1 −1 𝑥
̅
−1] 𝑣̅1,2 = 0 → 𝑓2 − 𝑓1 , 𝑓3 − 𝑓1 → [ 0
0
0 ] (𝑦) = 0̅ ~
𝑧
−1
0
0
0
𝑥
−1
0 ] (𝑦) = 0̅ → −𝑥 − 𝑦 − 𝑧 = 0 → 𝑧 = −𝑦 − 𝑥 ~
𝑧
0
𝑥
0
𝑥
𝑣̅1,2 = ( 𝑦 ) = ( 𝑦 ) + ( 0 )
−𝑦 − 𝑥
−𝑦
−𝑥
Entonces:
𝑥
1
𝑣̅1 = ( 0 ) , 𝑥 = 1 → 𝑣̅1 = ( 0 )
−𝑥
−1
0
0
𝑣̅2 = ( 𝑦 ) , 𝑦 = 1 → 𝑣̅2 = ( 1 )
−𝑦
−1
Aplicando Gram-Schmidt:
1
1
𝑥̅1 = ( 0 ) → 𝑥̂1 =
−1
√2
0
1
−
( √2)
0
1
( 1 )∙( 0 )
0
1
−1 ( 0 ) =
𝑥̅2 = ( 1 ) − −1
2
−1
−1
•
1
−
2
1 → 𝑥̂2 =
1
−
( 2)
−
1
√6
2
√6
1
−
( √6)
Para 𝜆2 = 4:
1 0 0
2 1 1
(4 [0 1 0] − [1 2 1]) 𝑣̅3 = 0̅
0 0 1
1 1 2
2 −1 −1
0 −3 3
[−1 2 −1] 𝑣̅3 = 0̅ → 𝑓1 + 2𝑓3 , 𝑓2 − 𝑓3 → [ 0
3 −3] 𝑣̅3 = 0̅ ~
−1 −1 2
−1 −1 2
0 −3 3
0
0
0
[0
3 −3] 𝑣̅3 = 0̅ → 𝑓1 + 𝑓2 → [ 0
3 −3] 𝑣̅3 = 0̅ ~
−1 −1 2
−1 −1 2
0
0
0
0
0 0
𝑓2
̅
[0
]
𝑣̅
=
0
→
,
−𝑓
→
[
3 −3 3
0 1 −1] 𝑣̅3 = 0̅ ~
3
3
−1 −1 2
1 1 −2
𝑥
0 0 0
0 0 0
[0 1 −1] 𝑣̅3 = 0̅ → 𝑓3 − 𝑓2 → [0 1 −1] (𝑦) = 0̅ ~
1 1 −2
1 0 −1 𝑧
𝑥
0 0 0
[0 1 −1] (𝑦) = 0̅ → 𝑦 − 𝑧 = 0, 𝑥 − 𝑧 = 0 → 𝑥 = 𝑦 = 𝑧 ~
1 0 −1 𝑧
1
𝑥
1
1
𝑥
𝑣̅3 = ( ) , 𝑥 = 1 → 𝑣̅3 = (1) → 𝑥̅3 = (1) → 𝑥̂3 =
𝑥
1
1
Construyendo Q:
√3
1
√3
1
(√3)
1
−
1
1
√6 √3
√2
2
1
𝑄= 0
√6 √3
1
−
1
1
√2 −
[
√6 √3]
Además:
1 0
𝐷 = 𝑄 𝑇 𝐴𝑄 = [0 1
0 0
0
0]
4
Semana 9:
7. Formas Cuádricas.
Definición:
Sea 𝑥̅ ∈ 𝑀𝑎𝑡𝑛𝑥1 (ℝ) la matriz de incógnitas y sea 𝐴 ∈ 𝑀𝑎𝑡𝑛𝑥𝑛 (ℝ) (simétrica) la
matriz asociada a la forma cuadrática.
𝑃(𝑥1 , … , 𝑥𝑛 ) = 𝑥̅ 𝑇 𝐴𝑥̅
Ejemplo 6:
Sea 𝑃(𝑥, 𝑦) = 𝑥 2 − 𝑦 2 + 2𝑥𝑦
Podemos definir:
𝑥
𝑥̅ = (𝑦)
Hallamos A:
𝑃(𝑥, 𝑦) = 𝑥 2 + 𝑥𝑦 + 𝑦𝑥 − 𝑦 2
1
𝐴=[
1
1
]
−1
Hallando el polinomio característico:
1 0
1 1
𝑃2 (𝜆) = |𝜆 [
]−[
]|
0 1
1 −1
𝜆 − 1 −1
𝑃2 (𝜆) = |
|
−1 𝜆 + 1
𝑃2 (𝜆) = (𝜆 − 1)(𝜆 + 1) − (−1)(−1)
𝑃2 (𝜆) = 𝜆2 − 1 − 1
𝑃2 (𝜆) = (𝜆 + √2)(𝜆 − √2)
Encontrando los valores propios:
𝑃2 (𝜆𝑖 ) = 0
(𝜆 + √2)(𝜆 − √2) = 0
𝜆1 = −√2 , 𝜆2 = √2
Encontrado los vectores propios reemplazando en (2):
•
Para 𝜆1 = −√2:
1
(−√2 [
0
0
1
]−[
1
1
1
]) 𝑣̅1 = 0̅
−1
𝑥
0
−1 ] 𝑣̅ = 0̅ → 𝑓 − (√2 + 1)𝑓 → [ 0
[−√2 − 1
] (𝑦) = 0̅ ~
1
1
2
−1 −√2 + 1
−1
−√2 + 1
𝑥
0
0
[
] ( ) = 0̅ → −𝑥 − (√2 − 1)𝑦 = 0 → 𝑦 = −𝑥 (√2 + 1)~
−1 −√2 + 1 𝑦
𝑥
1
)
𝑣̅1 = (−𝑥 (√2 + 1)) , 𝑥 = 1 → 𝑣̅1 = (
− (√2 + 1)
•
Para 𝜆1 = √2:
(√2 [
1 0
1 1
]−[
]) 𝑣̅2 = 0̅
0 1
1 −1
𝑥
0
−1 ] 𝑣̅ = 0̅ → 𝑓 + (√2 − 1)𝑓 → [ 0
[√2 − 1
] (𝑦) = 0̅ ~
2
1
2
−1 √2 + 1
−1
√2 + 1
𝑥
0
0
[
] ( ) = 0̅ → −𝑥 + (√2 + 1)𝑦 = 0 → 𝑦 = 𝑥 (√2 − 1)~
−1 √2 + 1 𝑦
𝑥
1
)
𝑣̅2 = (𝑥 (√2 − 1)) , 𝑥 = 1 → 𝑣̅2 = (
√2 − 1
Verificando:
1
1
)(
)=0
𝑣̅1 ∙ 𝑣̅2 = (
− (√2 + 1) √2 − 1
1
𝑣̂1 =
√4 + 2√2
√2 + 1
−
( √4 + 2√2)
1
𝑣̂2 =
√4 − 2√2
√2 − 1
(√4 − 2√2)
Construyendo Q:
1
𝑄=
1
√4 + 2√2
√4 − 2√2
√2 + 1
√2 − 1
−
[ √4 + 2√2 √4 − 2√2]
𝑥̅ 𝑇 𝐴𝑥̅ = 𝑥̅ 𝑇 𝑄𝐷𝑄 𝑇 𝑥̅ = (𝑄 𝑇 𝑥̅ )𝑇 𝐷(𝑄 𝑇 𝑥̅ )
1
𝑄 𝑇 𝑥̅ =
√4 + 2√2
1
[√4 − 2√2
−
√2 + 1
√4 + 2√2 𝑥
𝑢
(𝑦) = ( )
𝑣
√2 − 1
√4 − 2√2 ]
En el Plano:
•
Círculo:
(𝑥 − ℎ)2 (𝑦 − 𝑘)2
+
=1
𝑟2
𝑟2
•
Elipse
(𝑥 − ℎ)2 (𝑦 − 𝑘)2
+
=1
𝑎2
𝑏2
•
Parábola
(𝑦 − 𝑘)2 = 𝑎(𝑥 − ℎ)
(𝑥 − ℎ)2 = 𝑎(𝑦 − 𝑘)
•
Hipérbola
(𝑦 − 𝑘)2 (𝑥 − ℎ)2
−
=1
𝑎2
𝑏2
(𝑥 − ℎ)2 (𝑦 − 𝑘)2
−
=1
𝑎2
𝑏2
En el Espacio:
•
Esfera:
(𝑥 − ℎ)2 (𝑦 − 𝑘)2 (𝑧 − 𝑙)2
+
+
=1
𝑟2
𝑟2
𝑟2
•
Elipsoide
(𝑥 − ℎ)2 (𝑦 − 𝑘)2 (𝑧 − 𝑙)2
+
+
=1
𝑎2
𝑏2
𝑐2
•
Cono elíptico
(𝑥 − ℎ)2 (𝑦 − 𝑘)2 (𝑧 − 𝑙)2
+
−
=0
𝑎2
𝑏2
𝑐2
•
Paraboloide elíptico
(𝑥 − ℎ)2 (𝑦 − 𝑘)2
+
− (𝑧 − 𝑙) = 0
𝑎2
𝑏2
•
Paraboloide hiperbólico
(𝑥 − ℎ)2 (𝑦 − 𝑘)2
+
+ (𝑧 − 𝑙) = 0
𝑎2
𝑏2
•
Hiperboloide de un manto
(𝑥 − ℎ)2 (𝑦 − 𝑘)2 (𝑧 − 𝑙)2
+
−
=1
𝑎2
𝑏2
𝑐2
•
Hiperboloide de dos mantos
(𝑥 − ℎ)2 (𝑦 − 𝑘)2 (𝑧 − 𝑙)2
−
−
=1
𝑎2
𝑏2
𝑐2