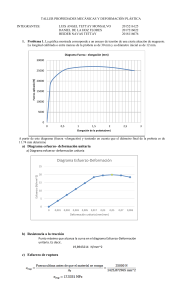
INFORME DE LABORATORIO MATERIALES DE INGENIERÍA ENSAYO DE TENSIÓN DOCENTE: SANDRA PATRICIA ROMERO DIEGO ANDRES ALVAREZ CD 129343 OSCAR IVÁN PÉREZ RUIZ CD 129262 HERSON ARVEY MOLINA CD 131528 UNIVERSIDAD ECCI INFORME DE LABORATORIO ENSAYO DE TENSIÓN Fecha Integrantes Responsable de laboratorio Responsable de pruebas Materiales Maquina universal de ensayos de tensión ECCI 04/11/24 Oscar Iván Pérez, Diego Álvarez, Herson Arvey Molina Profesora Sandra Patricia Romero. Joseph Encargado de operación de la MUDET (calibración de parámetros de velocidad para pruebas en diferentes materiales y entrega de graficas) 01 probeta de bronce latón 01 probeta de aluminio 01 probeta de polímero Procedimiento. Se realizará un reconocimiento de la maquina universal de pruebas. (Partes, tipos de mordazas, recomendaciones de seguridad, ejecución de ejercicios, toma de datos, registro fotográfico). Herramientas probetas Calibrador pie de rey medidas en milésimas Elementos de seguridad. Medidas finales (El uso de mono gafas y guantes es obligatorio), Bata, botas de seguridad Bronce latón: Inicial en promedio ø 4 mm - final ø 3.4 mm Se distingue una rebaja considerable en el diámetro de la probeta de y en la ruptura se demuestra una fractura de aspecto fibrosa y opaca, también se descubre de tipo copa y macho en cada uno de los extremos, por lo cual decimos que sufre una deformación plástica, y dúctil además un aumento en su longitud de Mas 2.5 mm, longitud final de 23.5 mm. En la grafica se distingue una zona elástica cuando se aplica una fuerza de 1500 a 5000 N, y los limites de ruptura y máximo esfuerzo. Esfuerzo a la fluencia Ductilidad Módulo de elasticidad elongación Reducción de área Zona elástica 𝜎= 𝐹 = 𝐴 6103.4551 𝑁 2 = 486 𝑀𝑃𝑎 4 𝑥 10−3 𝑚 ) 3.14 𝑥 ( 2 𝐿𝑓− 𝐿0 Δ𝐿 23.5 𝑚𝑚 − 21 𝑚𝑚 𝛿= = = = 0.11 𝐿1 𝐿0 21 𝑚𝑚 𝜎 6103.4551 𝑃𝑎 𝐸= = = 55.485 𝐾𝑃𝑎 𝛿 0.11 0.11 𝑥 100 = 11% ∆𝐴 9.07 𝑥 10−6 𝑚2 − 1.256 𝑋 10−5 𝑚2 =∈= 𝐴0 1.256 𝑋 10−5 𝑚2 = −277.8 𝑥 10−3 𝑥 100 = −27% X = 21.0 MPa y = 5000 N (pendiente naranja) ∈= Aluminio: Inicial en promedio ø 4 mm - final ø 3.4 mm Es de tipo de copa y cono con reducción en notoria en diámetro de 1.59 mm diámetro final es de 2.54 mm, longitud final de 25.72 mm muestra un aumento de 4.02 mm (presenta una fractura dúctil.) En la grafica se evidencian los puntos máximos de ruptura, limites elástico y plástico. Esfuerzo a la fluencia Ductilidad Módulo de elasticidad elongación 𝜎= 𝐹 = 𝐴 2903.8167 𝑁 2 = 216.86 𝑀𝑃𝑎 4.13 𝑥 10−3 𝑚 ) 3.14 𝑥 ( 2 𝐿𝑓− 𝐿0 Δ𝐿 25.72 𝑚𝑚 − 21.70 𝑚𝑚 𝛿= = = = 0.185 𝐿1 𝐿0 21.70 𝑚𝑚 𝜎 1.46 𝑥 109 𝑃𝑎 𝐸= = = 7.9 𝐺𝑃𝑎 𝛿 0.185 0.185 𝑥 100 = 18.5% Reducción de área Zona elástica Polímero (polipropileno) ∆𝐴 9.07 𝑥 10−6 𝑚2 − 1.34 𝑥 10−5 𝑚2 ∈= =∈= 𝐴0 1.34 𝑥 10−5 𝑚2 = −323.1 𝑥 10−3 𝑥 100 = −32.3% X = 1.3 MPa Y = 2400 N Para este material observamos una fractura de tipo dúctil, presentando una apariencia opaca con una deformación plástica, es de difícil observación, pero denota una fractura de forma copa y cono. Presentó una reducción en su espesor bajo de 2.65 mm a 2.44 mm y una diferencia en longitud de 3.2 mm y en el ancho de 2 mm, También observamos su grafica y limites de ruptura, fluencia, y limite elástico Esfuerzo a la fluencia Ductilidad Módulo de elasticidad elongación Reducción de área Conclusión 𝐹 1148.000 𝑁 = = 1.01 𝑇𝑃𝑎 −3 𝐴 ((14 𝑥 10 𝑚) 𝑥 ((2.44 𝑥 10−3 𝑚))2 𝐿𝑓− 𝐿0 Δ𝐿 179.2 𝑚𝑚 − 176 𝑚𝑚 𝛿= = = = 0.02 𝐿1 𝐿0 176 𝑚𝑚 𝜎 101 𝑥 1012 𝑃𝑎 𝐸= = = 5.05 𝑃𝑃𝑎 𝛿 0.02 0.02 𝑥 100 = 2% 2 1.59 𝑥 10−3 𝑚 3.14 𝑥 ( ) = 1.99 𝑥 10−6 𝑥 100 2 Los ensayos de tensión realizados proporcionaron información significativa sobre las propiedades mecánicas de los materiales evaluados: aleación de aluminio, latón y polipropileno. Mediante el análisis de las curvas esfuerzo-deformación, se identificaron el comportamiento elástico y plástico de cada material, así como parámetros esenciales como la resistencia máxima a la tracción, el módulo de elasticidad y la elongación total previa a la fractura. Estos resultados destacan la relevancia de los ensayos de tensión para seleccionar adecuadamente los materiales en función de sus propiedades mecánicas y su aplicabilidad en distintos contextos 𝜎=