cournot duopilio stakel EJERCICIOS

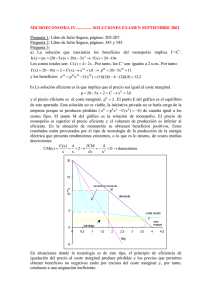
lOMoARcPSD|29770908
Ejercicios resueltos T12
Microeconomía Intermedia (Universidad de Castilla La Mancha)
Escanea para abrir en Studocu
Studocu no está patrocinado ni avalado por ningún colegio o universidad.
Descargado por Luis Torrez ([email protected])
lOMoARcPSD|29770908
! EJERCICIO 1. EL MODELO DE COURNOT Y EL DEL CÁRTEL SIN COSTES DE PRODUCCIÓN.
Supongamos dos empresas idénticas que se enfrentan a una curva lineal de demanda del mercado p = 30 - Q, donde Q
= q1 + q2. El coste marginal es nulo para ambas empresas.
1. ¿Cómo se obtienen las funciones de reacción de las dos empresas? ¿Cuál es el equilibrio de Cournot?
2. Obtenga la solución colusiva (cártel) y la competitiva y compárelas con la de Cournot
Soluciones
1. ¿Cómo obtenemos la función de reacción? ¿Cuál es el equilibrio de Cournot?
Se obtienen a partir de la maximización de la función de beneficios que, en este caso en que los costes son cero, es igual
a la función de ingreso total.
despejando q1 hallamos la función de reacción de la empresa 1:
la función de reacción de la empresa 2:
. Realizando el mismo cálculo obtendremos
. Las funciones de reacción de las empresas son simétricas porque
las empresas tienen los mismos costes.
Los niveles de producción de equilibrio son los valores de q1 y q2 que se encuentran en el punto de intersección
de las dos curvas de reacción. Es decir, son los niveles de producción que resuelven el sistema formado por las dos
funciones de reacción. El sistema lo resolvemos sustituyendo q2 en la función de reacción de la empresa 1:
Por lo tanto, en el equilibrio de Cournot:
precio:
. Los beneficios (=
. La cantidad producida total es:
y el
) serán iguales para los dos empresas: B1 = B2 = 100. En la
figura 1 se representa este equilibrio.
Figura 1. Los equilibrios de Cournot, colusión y competitivo.
2. Obtenga la solución colusiva y la competitiva y compárelas con la de Cournot
Hemos supuesto que las dos empresas compiten. Supongamos ahora que pueden coludir y que deciden maximizar los
beneficios conjuntamente. Los beneficios totales se maximizan eligiendo aquel nivel de producción total en el que el
ingreso marginal es igual al coste marginal (que en este caso es cero). La cantidad que maximiza el beneficio conjunto
es:
-1-
Descargado por Luis Torrez ([email protected])
lOMoARcPSD|29770908
Cualquier combinación de niveles de producción q1 y q2 que sume 15 maximiza el beneficio total. La curva q1
+ q2 = 15, llamada curva de colusión, indica los pares de niveles de producción que maximizan el beneficio total. Si las
empresas decidieran repartirse por igual los beneficios cada una produciría la mitad del total
(figura 1).
Como las dos empresas producen menos que en Cournot tendrán más beneficios al ser el precio mayor.
Los beneficios serán:
También se muestra en la figura 1 el equilibrio competitivo que se determina igualando el coste marginal y el
precio. Comprueben que
, y que el precio y los beneficios son cero.
! EJERCICIO 2. EL MODELO DE COURNOT CON COSTES DE PRODUCCIÓN
Dos empresas se enfrentan a la curva de demanda del mercado
. Las funciones de coste son
.
1. ¿Cuál es el equilibrio de Cournot? Represente gráficamente el equilibrio indicando la expresión de la función de
reacción de cada una de las dos empresas.
2. ¿Cuál de las dos empresas tiene el menor ingreso marginal?
Soluciones
1. ¿Cuál es el equilibrio de Cournot?
Formamos las funciones de beneficios de las dos empresas, las derivamos, las igualamos a cero y despejamos q1 en la
primera y q2 en la segunda:
Con las dos funciones de reacción formamos un sistema de ecuaciones que resuelto nos da las cantidades que las
empresas producirán en equilibrio, conocidas las cantidades podemos obtener el precio y con él los beneficios:
Como las empresas tienen distintas funciones de coste, las funciones de reacción no son simétricas y los
duopolistas no producen la misma cantidad ni obtienen los mismos beneficios (figura 2).
-2-
Descargado por Luis Torrez ([email protected])
lOMoARcPSD|29770908
Figura 2. Equilibrio Cournot-Nash.
2 .¿Cuál de las dos empresas tiene el menor ingreso marginal?
La empresa que produce menos tiene mayor ingreso marginal:
IMg1 = IT1/ q1 = pq1 / q1 = p + q1 p/Q
IMg1 = 45 + 80 (- 0,5) = 5
IMg2 = IT2/ q2 = pq2 / q2 = p + q2 p/Q
IMg2 = 45 +30 (- 0,5) = 30
Como: IMgi = CMgi ; IMg1 = CMg1 = 5 y IMg2 = CMg2 = q2 = 30
! EJERCICIO 3. EL MODELO DE COURNOT
Suponga dos empresas (las empresas 1 y 2) que venden un producto homogéneo. La demanda del mercado a la que se
enfrentan es:
y las funciones de coste de las empresas son:
,
respectivamente;
1. ¿Cuál es la solución de Cournot? (Precio, cantidades vendidas y beneficios de cada una de las empresas).
Solución
La función de demanda es
. El equilibrio se alcanza en el punto en el que se cortan las
funciones de reacción de las empresas.
-3-
Descargado por Luis Torrez ([email protected])
lOMoARcPSD|29770908
! EJERCICIO 4. EL MODELO DE COURNOT
En un mercado hay dos empresas con funciones de coste:
y
, respectivamente. Si la demanda del
mercado es
,
1. Determine la solución de Cournot (precio de mercado y cantidades producidas por cada empresa).
Solución
Por lo tanto:
,y
! EJERCICIO 5. EL MODELO DE COURNOT Y EL CÁRTEL
El mercado de un determinado bien homogéneo es suministrado por dos empresas: las empresas 1 y 2. Las funciones de
coste de cada una de ellas son, respectivamente,
y
. Si la función de demanda de mercado
del bien es
:
1. ¿A qué precio se venderá el producto si las empresas se comportan como duopolistas de Cournot?
2. Si ambas empresas forman un cártel, ¿qué cantidad del producto se ofertará entre las dos empresas?
3. Si la empresa 2 rompiera los acuerdos del cártel mientras que la 1 los mantiene, ¿qué precio se fijaría en el mercado?
Soluciones
1. ¿A qué precio se venderá el producto si las empresas se comportan como duopolistas de Cournot?
Solo tenemos que plantear las funciones de beneficios de las dos empresas y, a partir de ellas, obtener las funciones de
reacción:
Resolviendo el sistema formado por las dos funciones de reacción:
La producción total es
, por lo tanto, el precio único (común a las dos empresas)
-4-
Descargado por Luis Torrez ([email protected])
lOMoARcPSD|29770908
al que se venderá el producto será:
.
2. Si ambas empresas forman un cártel, ¿qué cantidad del producto se ofertará entre las dos empresas?
Simplemente, se trata de igualar el ingreso marginal a los costes marginales de las empresas, como en el caso de un
monopolio con varias plantas:
De la primera ecuación obtenemos:
; y sustituyendo en la
segunda:
.
Y sustituyendo en la primera ecuación:
las dos empresas es:
. Por lo tanto, la cantidad producida y ofertada por
.
3.. Si la empresa 2 rompiera los acuerdos del cártel mientras que la 1 los mantiene, ¿qué precio se fijaría en el
mercado?
Los acuerdos del cártel implican que cada empresa produzca una unidad. Si la empresa 2 rompe el acuerdo, pero la 1 lo
mantiene, el problema que tiene que resolver la empresa 2 es maximizar el beneficio sujeto a la condición de que la
empresa 1 produzca una unidad.
Por lo tanto, la cantidad producida y ofertada en total es:
, por lo que el precio al que se venderá
será:
! EJERCICIO 6. EL MODELO DE STACKELBERG SIN COSTES DE PRODUCCIÓN
Supongamos que dos empresas tienen un coste marginal nulo y que la curva de demanda del mercado viene dada por la
expresión p = 30 - Q, donde Q es la producción total. Supongamos que la empresa 1 es la líder.
1. ¿Qué cantidad produce cada empresa?
2. ¿Por qué es ventajoso desde el punto de vista estratégico ser el primero?
Soluciones
1. ¿Qué cantidad produce cada empresa?
Comencemos por la empresa 2. Considera dado el nivel de producción de la 1. Por lo tanto, su nivel de producción que
maximiza los beneficios viene dado por su función de reacción (vea el ejercicio 1):
. ¿Cómo se comportará
la empresa 1? Para maximizar sus beneficios elige su nivel de producción de forma tal que su ingreso marginal sea igual
a cero. Dada la curva de demanda, la de ingreso total será:
. Como el ingreso marginal de
la 1 depende del nivel de producción de la 2, la empresa 1 debe prever cuánto producirá la 2. Sin embargo, la 1 sabe que
la 2 elegirá su producción de acuerdo con su función de reacción. Sustituyendo en la función de ingreso la función de
reacción de la empresa 2, observamos que el ingreso de la empresa 1 es
por lo que su ingreso marginal será:
Igualando el IMg1 a cero, tenemos que q1 = 15. Y a partir de la función de reacción de la empresa 2 calculamos que q2 =
-5-
Descargado por Luis Torrez ([email protected])
lOMoARcPSD|29770908
7,5. La empresa 1 produce el doble que la 2 y obtiene el doble de beneficios. La empresa uno tiene ventaja por ser la
primera.
2. ¿Por qué es ventajoso desde el punto de vista estratégico ser el primero?
La razón se halla en que el que anuncia primero se presenta con un hecho consumado: su nivel de producción será elevado
independientemente de lo que haga su competidor. Para maximizar sus beneficios el competidor debe considerar dado el
elevado nivel de producción de la líder y fijarse un nivel bajo.(Si produjera un nivel de producción elevado, presionaría
a la baja sobre el precio y perdería dinero, por lo que, a menos que el competidor, la empresa seguidora, considere que no
perder dinero es más importante que ganarlo, es irracional que produzca una gran cantidad). La ventaja de mover primero
se da en muchas situaciones estratégicas.
! EJERCICIO 7. EL MODELO DE STACKELBERG CON COSTES DE PRODUCCIÓN
Suponga que en un mercado duopolista la función de demanda es:
y que los costes de los
duopolistas, son:
, respectivamente.
1. Determine las funciones de reacción de las dos empresas considerando que la empresa 2 es la líder y obtenga la
solución del modelo.
Soluciones
1. Determine las funciones de reacción de las dos empresas considerando que la empresa 1 es la líder
Consideramos una función de demanda lineal
y una función de coste también lineal. La función de
beneficios de la empresa 1, que es la líder, será:
Y la función de reacción de la empresa 2
. En el equilibrio de Stackelberg, la empresa líder elige q1 para maximizar sus beneficios sujeta a la
es:
restricción de que la 2 elige q2. en su función de reacción. Por lo tanto, introduciendo la función de reacción de la 2 en la
función de beneficios de la 1 y maximizando, obtenemos
e introduciendo este valor en la función de reacción de la empresa 2:
Una característica ambigua del modelo de Stackelberg es cómo se elige la líder cuando las dos empresa son
“sagaces” a la manera de Stackelberg.
Cada duopolista estima el beneficio máximo que obtendría: a) si actuara como líder, b) si actuara como seguidora
y escogerá el comportamiento que le proporcione el mayor beneficio. Pueden presentarse cuatro soluciones posibles:
1. La empresa 1 es la líder y la 2 es la seguidora.
2. La empresa 2 es la líder y la 1 la seguidora.
3. Ambas empresa quieren ser seguidoras (equilibrio de Cournot)
4. Ambas empresas quieren ser líderes.
En las situaciones 3 y 4 el resultado es un equilibrio indefinido. Si ambas empresas desean ser seguidoras, sus
expectativas no se cumplirán (ya que cada una supone que su rival se comportará como líder) y deberán revisarlas. Hay
dos posibilidades. Si cada empresa se da cuenta que la otra desea ser seguidora se alcanzará un equilibrio de Cournot. Si
no, una de las dos empresas deberá modificar su comportamiento y actuar como líder para alcanzar un equilibrio. Por
último, si ambas empresas quieren ser líderes se produce un desequilibrio cuya consecuencia, según Stackelberg, es la
guerra económica. El equilibrio se alcanzará mediante un pacto de colusión, o cuando la empresa más débil de las dos sea
eliminada o sucumba al liderazgo de la otra.
Según el enunciado, la función de demanda es
y los costes de los duopolistas son:
y
. Las funciones de reacción se obtienen, a partir de las derivadas parciales de las funciones de
beneficios igualadas a cero.
Las funciones de beneficios son:
-6-
Descargado por Luis Torrez ([email protected])
lOMoARcPSD|29770908
Las derivadas parciales de la funciones de beneficios y las funciones de reacción son:
Si la empresa 2 es la líder, sustituimos la función de reacción de la empresa 1 en la de beneficios de la 2 y
obtenemos la cantidad que producirá la empresa líder (la 2) para maximizar sus beneficios:
Sustituyendo esta cantidad en la función de reacción de la empresa 1, obtenemos la cantidad que producirá la
empresa 1 (la seguidora):
por lo tanto,
y el precio (un precio común para las dos empresas porque el bien es
homogéneo) al que se vende el bien es:
Los beneficios serán
Aunque la empresa 2 obtiene menos beneficios que la empresa 1, obtiene más que si se comportara como
seguidora. Compruébelo.
! EJERCICIO 8. EL MODELO DE STACKELBERG
La demanda de mercado de un bien es
. En el mercado actúan dos empresas que producen con las funciones
de coste
, respectivamente.
1. Calcule el equilibrio en el modelo de Stackelberg si la empresa 1 actúa como líder.
Solución
! Función de reacción de la empresa 2:
! La empresa líder maximiza beneficios de forma independiente.
La empresa 2 producirá lo que determine su función de reacción:
Conjuntamente producen:
será:
.
. Por lo que el precio al que se venderá el producto
.
-7-
Descargado por Luis Torrez ([email protected])
lOMoARcPSD|29770908
! EJERCICIO 9. EL MODELO DE LA EMPRESA DOMINANTE Y EL DE STACKELBERG
1. Consideremos una industria con 50 empresas que actúan de manera competitiva y que venden un determinado producto
que tiene una demanda: Q = 950 - 50p; las empresas tienen idénticas funciones de coste a corto plazo, que vienen dadas
por la expresión: CTi = qi2 /32 + 2qi +128. Establezca con precisión cuál es la curva de oferta de cada una de las
empresas. ¿Cuál es la curva de oferta de la industria?. ¿Cuál es la elasticidad precio de la oferta en el punto de
equilibrio?
2. El progreso técnico modifica la función de producción de las empresas de la industria y consecuentemente su función
de costes, que ahora pasa a ser CTi = qi2/ 2; pero permite también la aparición de una gran empresa en el mercado que
produce con costes marginales nulos y que por sus dimensiones se convierte en la empresa dominante en la industria.
Además, se produce un incremento de la demanda del producto, pues si antes para un precio cero se demandaban 950
unidades ahora se demandan 1000. Determine la cantidad y el precio que maximizan los beneficios de la empresa
dominante; la cantidad ofrecida por el sector competitivo; y represente gráficamente la situación.
3. Las empresas pequeñas se fusionan en una sola empresa, consiguiendo con la fusión reducir sus costes marginales a
cero, con lo que habrá dos empresas en el mercado. La antigua empresa dominante piensa que podrá seguir comportándose
como un monopolio creyendo que la otra empresa se adaptará a la cantidad que ella produzca. La nueva empresa grande
(la resultante de la fusión de las pequeñas) cree lo mismo. Cuál será la situación que se alcanzará en un primer momento,
y cuál una posible solución final.
Soluciones
1. Consideremos una industria con 50 empresas que actúan de manera competitiva y que venden un determinado
producto que tiene una demanda: Q = 950 - 50p; las empresas tienen idénticas funciones de coste a corto plazo, que
vienen dadas por la expresión: CTi = qi2 /32 + 2qi +128. Establezca con precisión cuál es la curva de oferta de cada
una de las empresas. ¿Cuál es la curva de oferta de la industria?. ¿Cuál es la elasticidad precio de la oferta en el
punto de equilibrio?
La curva de oferta nos da la cantidad que la empresa representativa ofrece a cada precio de forma que se maximicen los
beneficios. La empresa en competencia perfecta maximiza beneficios igualando su coste marginal al precio del mercado
(la empresa es precio aceptante). Necesitamos conocer el coste marginal y la podemos obtener a partir de la función de
costes del enunciado. CMg = q/16 + 2. De donde, p = q/16 +2  q = 16p - 32, por lo tanto: q = 16(p - 2) para p  2.
Observe, que si p < 2 la empresa no ofrece nada (para un precio menor que dos la cantidad que resulta de la aplicación
de la función de oferta es negativa). La curva de oferta corta al eje de los precios para p = 2.
Como el coste variable medio (CVMe) es [(q/32) + 2], su representación gráfica es una línea recta con pendiente
positiva (su derivada con respecto a q es una constante 1/32) y menor que el coste marginal para toda cantidad producida
mayor que cero. En consecuencia, la curva de oferta de la empresa es la de su coste marginal en toda su extensión. La
empresa ofrece el bien para precios mayores que 2 (al precio 2 la cantidad ofrecida sera cero).
La oferta de la industria será la suma de la oferta de cada una de las empresas, puesto que todas ellas tienen la
misma función de costes y por lo tanto idéntica función de oferta:
para p > 2,
Dada la demanda, Q D = 950 - 50p, la cantidad y el precio de equilibrio serán (figura 1):
La cantidad producida y vendida por cada empresa será:
qi = 16(p - 2) = 16(3 - 2) = 16.
La elasticidad de la curva de oferta de cada empresa se
obtiene fácilmente aplicando la formula de la elasticidad,
 = dq /dp p/q = [p /16(p - 2)]16 = p / (p - 2).
Para el precio de equilibrio que es 3, la elasticidad precio
es  = 3/ (3-2) = 3. La elasticidad de la curva de oferta de la
industria es también 3 [Las curvas de oferta individuales y la
agregada tienen elasticidad mayor que uno, puesto que cortan el eje
de precios y son lineales. Además la elasticidad es la misma en
todos los puntos para las dos curvas].
Figura 1.
-8-
Descargado por Luis Torrez ([email protected])
lOMoARcPSD|29770908
2. El progreso técnico modifica la función de producción de las empresas de la industria y consecuentemente su
función de costes, que ahora pasa a ser CTi = qi2/2; pero permite también la aparición de una gran empresa en el
mercado que produce con costes marginales nulos y que por sus dimensiones se convierte en la empresa dominante
en la industria. Además, se produce un incremento de la demanda del producto, pues si antes para un precio cero
se demandaban 950 unidades ahora se demandan 1000. Determine la cantidad y el precio que maximizan los
beneficios de la empresa dominante; la cantidad ofrecida por el sector competitivo; y represente gráficamente la
situación.
Empecemos con la demanda, si antes la demanda era Q = 950 - 50p y ahora se demandan 1000 unidades al precio cero,
la nueva demanda del mercado será Q = 1000 - 50p. Los costes de las empresas competitivas han disminuido, han pasado
a ser, CTi = qi2/2. Por lo tanto, se ha modificado también la curva de oferta de cada una de las empresas competitivas.
Como antes, obtenemos el coste marginal a partir de la función de coste: CMgi = qi, y el coste medio (ahora estamos en
el largo plazo, observe que en la función de coste no aparece ningún término no afectado por la cantidad producida, es
decir, no hay costes fijos) es q/2, menor que el coste marginal para todo valor de q y que pasa por el punto del origen de
coordenadas. Por lo tanto, la curva de oferta de la empresa es la de coste marginal en toda su extensión, y la determinamos
igualando el coste marginal al precio: qi = p, para todo p  0.
La curva de oferta conjunta de las empresas competitivas será:
La empresa dominante se comporta como un monopolio, pero permite que las empresas pequeñas sobrevivan
dejándolas vender todo lo que puedan al precio que fija ella. Es decir, las empresas pequeñas siguen siendo precio
aceptantes, pero ahora es la empresa dominante la que fija el precio, no el mercado.
La empresa dominante determina la cantidad a producir estableciendo “su curva de demanda”,
, que es la
demanda del mercado, la cantidad demandada a cada precio, menos la cantidad que a cada precio ofrece el conjunto de
las empresas pequeñas. La obtendremos, por lo tanto, restando a la curva de demanda del mercado la curva de oferta
agregada de las empresas pequeñas
; es decir:
, y, por lo tanto:
La empresa dominante maximiza los beneficios igualando el ingreso marginal al coste marginal, pero como para
la empresa del enunciado los costes marginales son nulos, igualará el ingreso marginal (IM) a cero. Dada la curva de
demanda de la empresa dominante p = 10 - 0,01Q, el ingreso total (IT) sera, IT = 10Q - 0,01Q 2, y el ingreso marginal:
IM = 10 - 0,02Q. La condición de equilibrio es: 10 - 0,02Q = 0, de donde:
Sustituyendo la cantidad que maximiza el beneficio de la dominante (500) en la función de demanda, el precio
de equilibrio será p = 10 - 0,01 (500) = 5. Las empresas pequeñas, en conjunto, podrán vender la cantidad que determine
su curva de oferta: Q s C = 50P = 50 (5) = 250. Y cada una de ellas, qi = 250/50 = 5 (figura 2). [Comprobación: la empresa
dominante y las empresas pequeñas producen conjuntamente 750 unidades (500 + 250); al precio fijado por la dominante
la cantidad demandada por el mercado es: 1000 - 50P = 1000 - 50 (5) = 1000 - 250 = 750. Y esa cantidad supone, dada
la demanda del mercado (p = 20
- 0,02Q), un precio de 5].
Figura 2. La empresa dominante produce 500, donde su ingreso
marginal corta al eje de las cantidades y las vende a un precio de
5. A ese precio las empresas pequeñas ofrecen conjuntamente 250,
donde la curva de oferta de las empresas pequeñas, la curva de
coste marginal de la figura, se iguala al precio 5. Al precio 5 la
cantidad demandada por el mercado es 750.
-9-
Descargado por Luis Torrez ([email protected])
lOMoARcPSD|29770908
3. Las empresas pequeñas se fusionan en una sola empresa, consiguiendo con la fusión reducir sus costes marginales
a cero, con lo que habrá dos empresas en el mercado. La antigua empresa dominante piensa que podrá seguir
comportándose como un monopolio creyendo que la otra empresa se adaptará a la cantidad que ella produzca. La
nueva empresa grande (la resultante de la fusión de las pequeñas) cree lo mismo. ¿Cuál será la situación que se
alcanzará en un primer momento, y cuál una posible solución final?
En esta parte se plantea un problema de duopolio. Las dos empresas producen con costes marginales nulos. Y las dos
quieren comportarse como líderes de Stackelberg. Es decir, quieren decidir la cantidad a producir como si fueran
monopolistas pensando que la otra empresa se adaptará a la cantidad producida por ellas. Con otras palabras, suponen que
la otra empresa se comportará a lo Cournot. Sin embargo, las dos empresas se comportan como líderes y, en consecuencia,
las dos ven fracasadas sus expectativas de beneficios. Al ser los costes marginales nulos, las dos empresas al maximizar
sus beneficios de forma independiente, igualando el ingreso marginal a cero, producirán para la mitad del mercado, y, en
conjunto, producirán para la totalidad del mercado, con lo que el precio correspondiente será cero, como también serán
cero sus beneficios. En un segundo momento, las dos empresas podrían optar por formar un cártel y evitar así la
competencia entre ellas.
Consideremos que la antigua empresa dominante sea la empresa 1, y la empresa resultante de la fusión de las
pequeñas empresas competitivas, la empresa 2. Formamos las funciones de beneficios de las dos empresas para obtener
las funciones de reacción:
Derivando las funciones de beneficios respecto de la producción de cada una de las empresas y despejando la
cantidad producida obtenemos la función de reacción de cada una de las empresas:
Consideremos, primero la empresa 1. Cree que la otra empresa, la 2, se comportará a lo Cournot y determina la
cantidad a producir de forma independiente sustituyendo en su función de beneficio la función de reacción de la empresa
2:
La empresa 1 piensa que la otra empresa producirá 250 unidades:
. Con
lo que el precio que espera el empresario 1 es:
Y el beneficio esperado:
.
Sin embargo, como la empresa 2 tiene la misma estrategia que la empresa 1 (cree que la otra empresa se adaptará
comportándose a lo Cournot), produce la misma cantidad que la empresa 1 (500 unidades), y por lo tanto, el precio del
mercado será cero: p = 20 - 0,02 (1000) = 0. Y el beneficio que obtienen las dos empresas será, también, cero. Se trata de
una solución inestable. Una posible solución sería que las dos empresas formaran un cártel y maximizaran conjuntamente
los beneficios. Producirían, puesto que no hay costes, para la mitad del mercado, 500, vendiendo cada unidad al precio
que establece la demanda: p = 20 - 0,02  500 = 20 - 10 = 10. Y los beneficios conjuntos serían, B = IT = 10  500 = 5000.
Como tienen los mismos costes producirían 250 cada una, y los beneficios se repartirían por igual, 2.500 unidades
monetarias para cada una.
! EJERCICIO 10. LA EMPRESA DOMINANTE
Supongamos que la curva de demanda del mercado es Q = a - bp. El seguidor tiene la función de costes CT2 = q22/2 y el
líder tiene la función de costes CT1 = cq1 .
-10-
Descargado por Luis Torrez ([email protected])
lOMoARcPSD|29770908
1. Plantee el modelo y represéntelo gráficamente
Soluciones
1. Plantee el modelo y represéntelo gráficamente
Consideramos que solo hay dos empresas una líder que fija el precio y una seguidora que fija el mismo precio que la líder.
Es decir, se trataría de una modelo simétrico al de Stackelberg en donde la empresa líder en lugar de fijar la cantidad fija
el precio. Por supuesto, para tomar una decisión sensata debe tener en cuenta a la seguidora, debe predecir su
comportamiento. Y por lo tanto debe plantearse la maximización de beneficios de la empresa seguidora. Esta empresa
considera que el precio escapa a su control puesto que ya ha sido fijado por el líder. Desea maximizar sus beneficios, es
decir, tiene que maximizar B = pq2 - c2 (q2), eligiendo un nivel de producción a partir d ela condición de que el precio sea
igual al coste marginal. Esta condición determina la curva de oferta del seguidor S(p). Pasemos al problema de la empresa
líder, ¿cuál es su curva de oferta? La empresa es consciente de que si fija un precio p, la otra ofertará S(p), lo que
significa que la cantidad que ella venderá será DD = D(p) - S(p), esta expresión es la curva de demanda residual del líder.
Supongamos que el coste marginal es constante, c. Los beneficios que obtiene cualquiera que sea el precio serán:
B = (p - c) [D(p) - S(p)] = DD (p - c)
Dado el precio p, la empresa precio aceptante desea elegir el nivel de producción en el que el precio es igual al
coste marginal. Si la función de costes es la mencionada, el coste marginal de la empresa es CMg = q2. Igualando el precio
y el coste marginal p = q2, que es la curva de oferta de la empresa: q2 = S(p) = p.
La curva de demanda a la que se enfrenta el líder, la llamada curva de demanda residual, es, DD = D(p) - S(P)
= a - b p - p = a - (b + 1)P. A partir de aquí estamos ante un problema ordinario de monopolio, poniendo la demanda
en forma inversa,
La curva de ingreso marginal será, teniendo en cuenta que la demanda es lineal y por lo tanto el ingreso marginal
tendrá la misma ordenada y la mitad de la abscisa:
Igualando el ingreso y el coste marginales y despejando el nivel de producción maximizador del beneficio del líder tenemos
que,
El precio lo obtendríamos sustituyendo esta expresión en la función de demanda inversa del líder.
Figura 1
! EJERCICIO 11. LA COLUSIÓN EXPLÍCITA: EL CÁRTEL
Sea p =100 - 0,5 (q1 + q2) la función de demanda a la que se enfrentan dos oligopolistas que fabrican un producto
homogéneo. Los costes de la empresa 1 son CT1 = 5q1, y los de la empresa 2, CT2 = 0,5q22. Suponga que las dos empresas
anteriores coluden explícitamente formando un cártel.
1. ¿Qué cantidad producirá cada empresa y qué beneficios obtendrá cada una de ellas? ¿Por qué una empresa produce
más que la otra?
Soluciones
-11-
Descargado por Luis Torrez ([email protected])
lOMoARcPSD|29770908
1. ¿Qué cantidad producirá cada empresa y qué beneficios obtendrá cada una de ellas? ¿Por qué una empresa
produce más que la otra?
Podemos resolverlo de dos formas diferentes:
! Maximizando los beneficios conjuntamente: B = B1 + B2
B1 =IT1 - CT1, y B2 = IT2 - CT2
B = (IT1 + IT2) - (CT1 + CT2) y B = p(q1 +q2) - CT1 - CT2 = [100 - 0,5(q1 + q2)] (q1 + q2) - 5q1 - 0,5q22 =
= 95q1 + 100q2 - 0,5q12 - q1q2 - q22
B1/q1 = 95 - q1 - q2 = 0
B2/q2 = 100 - q1 - 2q2 = 0
q2 = 50 - 0,5q1
95 - q1 - 50 + 0,5q1 = 0
q1 = 90
q2 = 50 - 0,5 (90) = 5
por lo tanto, Q = q1 + q2 = 95; y p = 100 - 0,5 (95) = 52,5
B1 = pq1 - CT1 = 52,5 (90) - 5 (90) = 4725 - 450 = 4275
B2 = pq2 - CT2 = 52,5 (5) - 0,5 (52) = 262,5 - 12,5 = 250
! Cumpliendo la condición de que el coste marginal de cada empresa se iguale al ingreso marginal (como en el monopolio
con varias plantas).
IMg = CMg1 = CMg2
IT = pQ = (100 - 0,5Q) Q = 100Q - 0,5Q2
IMg =100 - Q = 100 - q1 - q2
IMg = CMg1 y IMg = CMg2
100 - q1 - q2 = 5
100 - q1 - q2 = q2
Substituimos la primera ecuación, 95 - q2 = q1 , en la segunda:
100 - (95 - q2) - q2 = q2
q2 = 5; y q1 = 95 - 5 = 90
por lo tanto, Q = 95. Los costes marginales de las dos empresas se tienen que igualar al ingreso marginal, y el coste
marginal de la empresa 1 es constante e igual a 5, por eso produce más.
IMg = p + Q dp/dQ = 52,5 + 95 (- 0,5) = 5.
CMg1 = 5
CMg2 = q2 = 5
Como se comprueba observando los costes totales en la función de beneficios, los de la empresa 1 son mayores que los
de la empresa 2, pero es porque produce más.
-12-
Descargado por Luis Torrez ([email protected])