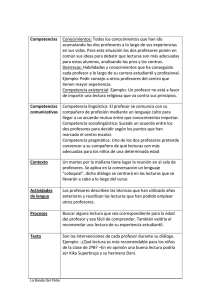
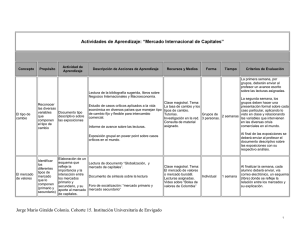
ESCUELA POLITECNICA NACIONAL CONSEJO DE DOCENCIA EPN-GD-MSP-03-03-PRD-05-FRM-02 SILABO Versión 2 UNIDAD ACADÉMICA: CARRERA: CIENCIAS (RRA20) MATEMÁTICA APLICADA PERIODO ACADÉMICO: 2024-B OCTUBRE 2024 FEBRERO 2025 TIPO: ORDINARIO DETALLE DE ASIGNATURA: NOMBRE: TEORIA DE LA MEDIDA E INTEGRACION PARALELO: A CÓDIGO: CRÉDITOS: MTMD513 PENSUM: MODALIDAD IMA.20.30.01 3.00 COMPONENTES DE ORGANIZACIÓN DE LOS APRENDIZAJES Aprendizaje en Contacto con el Docente (AC) Aprendizaje Práctico Experimental (AP) Aprendizaje Autónomo (AA) HORAS POR SEMANA TOTAL 5.00 1.00 3.0 9.00 PRESENCIAL HORAS POR PERIODO ACADEMICO 80 16 48 144 REQUISITOS DE LA ASIGNATURA CO-REQUISITOS PRE-REQUISITOS NOMBRE CÓDIGO NOMBRE LABORATORIO TEORIA DE LA MEDIDA E MTMD513L ANALISIS COMPLEJO INTEGRACION INTRODUCCION A LOS ESPACIOS METRICOS MTMD524 DE BANACH Y DE HILBERT CÓDIGO MTMD424 HORARIO DE LA ASIGNATURA: COMPONENTE DE APRENDIZAJES AC HORARIO MTMD513 - TEORIA DE LA MEDIDA E INTEGRACION - A - Lunes: 9-10 Miércoles: 9-11 Viernes: 7- 9 DESCRIPCIÓN DE LA ASIGNATURA: LA INTENCIÓN DE ESTE CURSO ES EL DE GENERALIZAR RIGUROSAMENTE LAS NOCIONES DE LONGITUD, ÁREA Y VOLUMEN, A TRAVÉS DE LOS CONCEPTOS DE MEDIDA E INTEGRACIÓN. POR ESTE MOTIVO, SE ESTUDIAN A PROFUNDIDAD LOS ESPACIOS DE MEDIDA Y FUNCIONES MEDIBLES. SE ABORDA TAMBIÉN LA INTEGRACIÓN SOBRE ESPACIOS DE MEDIDA, REALZANDO LOS TEOREMAS DE CONVERGENCIA MONÓTONA DE BEPPO--LEVI, CONVEGENCIA DOMINADA DE LEBESGUE Y DE FUBINI--TONELLI. SE HACE UN ÉNFASIS ESPECIAL EN LA MEDIDA DE LEBESGUE Y EN LAS PROPIEDADES DE LOS ESPACIOS DE LEBESGUE LP, PRIMORDIALES EN EL ESTUDIO DE LAS SOLUCIONES DE CIERTAS ECUACIONES EN DERIVADAS PARCIALES, EN LA TEORÍA DE PROBABILIDADES, Y DEMÁS ÁREAS DEL CONOCIMIENTO, DONDE LA INTEGRACIÓN JUEGA UN ROL FUNDAMENTAL. INFORMACIÓN DE PROFESOR(ES) A CARGO: NOMBRE CORREO YANGARI SOSA miguel.yangari@e MIGUEL ANGEL pn.edu.ec ROSADO CORDOVA EMILIO JOSE FORMACIÓN ACADÉMICA PARALELO COMPONENTE DE APRENDIZAJE DOCENTE PRINCIPAL DOCTOR EN CIENCIAS DE LA INGENIERIA, MENCION MODELACION MATEMATICA A AC X A AP emilio.rosado@ep n.edu.ec RESULTADOS DEL APRENDIZAJE DE LA ASIGNATURA: TIPO DE REUSLTADO Conocimientos DESCRIPCIÓN DEL RESULTADO FORMA DE EVIDENCIAR EL CUMPLIMIENTO** 1.1 DESCRIBIR LA CONSTRUCCIÓN DE LA MEDIDA EXTERIOR DE LEBESGUE. 1.2 ENUNCIAR Y DESCRIBIR LA DEMOSTRACIÓN DEL TEOREMA DE EXTENSIÓN DE CARATHÉODORY - HAHN. 1.3 DESCRIBIR LA CONSTRUCCIÓN DE LA MEDIDA DE LEBESGUE. 1.4 ILUSTRAR LA EXISTENCIA DE CONJUNTOS NO MEDIBLES. 1.5 ENUNCIAR Y DESCRIBIR LA DEMOSTRACIÓN DEL TEOREMA DE EGOROFF. El estudiante debe resolver ejercicios prácticos, además 1.6 ENUNCIAR Y DESCRIBIR LAS debe conocer la teoría y demostraciones DEMOSTRACIONES DE LOS TEOREMAS CLÁSICOS: FATOU, CONVERGENCIA DOMINADA Y DE TONELLI-FUBINI. 1.7 DESCRIBIR LAS SIMILITUDES Y DIFERENCIAS ENTRE LAS INTEGRALES DE RIEMANN Y DE LEBESGUE. 1.8 DESCRIBIR LAS PROPIEDADES ALGEBRAICAS, DE COMPLETITUD, SEPARABILIDAD, DENSIDAD Y REFLEXIVIDAD DE LOS ESPACIOS LP Destrezas Valores y actitudes 2.1 DEMOSTRAR QUE UNA CIERTA FUNCIÓN ES UNA MEDIDA. 2.2 DEMOSTRAR QUE UNA CIERTA FUNCIÓN ES UNA MEDIDA EXTERIOR. 2.3 DEMOSTRAR QUE UN CONJUNTO ES MEDIBLE. 2.4 DETERMINAR CUANDO UNA FUNCIÓN ES LEBESGUE INTEGRABLE. 2.5 CALCULAR LA INTEGRAL DE LEBESGUE DE FUNCIONES LEBESGUE INTEGRABLES. 2.6 DETERMINAR EL VALOR DE LA INTEGRAL DE LEBESGUE DE UNA FUNCIÓN A PARTIR DE LAS PROPIEDADES DE LAS FUNCIONES LEBESGUE INTEGRABLES. 2.7 APLICAR EL TEOREMA DE CONVERGENCIA DOMINADA DE LEBESGUE. 2.8 CONTRASTAR LAS PROPIEDADES DE LOS ESPACIOS LP CON LAS DE LOS ESPACIOS DE El estudiante debe resolver ejercicios prácticos, además SUCESIONES LP. debe conocer la teoría y demostraciones 2.9 CATEGORIZAR LOS ESPACIOS LP SEGÚN SUS PROPIEDADES DE REFLEXIVIDAD Y SEPARABILIDAD. 2.10 ESTABLECER LA CONEXIÓN ENTRELOS ESPACIOS LP Y LQ, CUANDO P Y Q SON EXPONENTES CONJUGADOS. 2.11 EMPLEAR LAS DESIGUALDADES DE HLDER Y DE MINKOWSKI EN LA CONSTRUCCIÓN DE LA ESTRUCTURA DE ESPACIO VECTORIAL NORMADO PARA LOS ESPACIOS LP. 2.12 EXPRESAR CADA FUNCIÓN EN LP COMO EL LÍMITE DE UNA SUCESIÓN DE FUNCIONES A SOPORTE COMPACTO. 2.13 DIFERENCIAR LOS DISTINTOS TIPOS DE CONVERGENCIA DE SUCESIONES DE FUNCIONES EN LP E IDENTIFICAR LA RELACIÓN ENTRE LAS MISMAS. 3.1 DISCRIMINAR ENTRE PROCESOS MECÁNICOS PARA LA SOLUCIÓN DE CIERTOS PROBLEMAS Y PROCESOS SUSTENTADOS Y EXPLICADOS POR UNA TEORÍA. 3.2 ADOPTAR COMO UNA ÉTICA MATEMÁTICA: LA NO ACEPTACIÓN DE ASEVERACIONES SIN LA CORRESPONDIENTE DEMOSTRACIÓN, Y LA REFLEXIÓN SOBRE EL SIGNIFICADO DE LAS MENCIONADAS ASEVERACIONES. 3.3 DEMOSTRAR CAPACIDAD DE ESTUDIO Y Actividades en clase TRABAJO EN EQUIPO. 3.4 DESARROLLAR EL SENTIDO DE RESPONSABILIDAD EN EL CUMPLIMIENTO DE LAS TAREAS, COMPROMISOS Y OBLIGACIONES. 3.5 DESARROLLAR LA CAPACIDAD DE AUTONOMÍA, EN PARTICULAR EN EL APRENDIZAJE, A FIN DE AMPLIAR Y PROFUNDIZAR LOS CONOCIMIENTOS MATEMÁTICOS. ** Descripciones específicas, medibles y demostrables de lo que el estudiante deberá hacer para el logro de los resultados del aprendizaje. CONTENIDOS Y ACTIVIDADES DE APRENDIZAJE DE LA ASIGNATURA DOCENTE: YANGARI SOSA MIGUEL ANGEL, PARALELO: A, COMPONENTE : AC N° 1 2 3 SEMANA SEMANA1 SEMANA2 SEMANA3 CONTENIDO COMPONENTE DE APRENDIZAJE HOR AS ACTIVIDADES DE APRENDIZAJE Espacios de medida - Álgebras, sigma álgebras y medidas. Medida de AC Lebesgue 5.0 AA 3.0 Espacios de medida - Álgebras, sigma álgebras y medidas. Medida de AC Lebesgue 5.0 AA 3.0 Exposición oral (clase magistral), ejercicios dentro de clase, lecturas dentro de clase Ejercicios fuera de clase, lecturas fuera de clase, búsqueda de información Exposición oral (clase magistral), ejercicios dentro de clase, lecturas dentro de clase Ejercicios fuera de clase, lecturas fuera de clase, búsqueda de información Espacios de medida - Álgebras, sigma álgebras y medidas. Medida de AC 5.0 Exposición oral (clase magistral), ejercicios dentro de clase, lecturas dentro Lebesgue AA 4 5 6 7 8 9 10 11 12 13 14 15 16 SEMANA4 SEMANA5 SEMANA6 SEMANA7 SEMANA8 SEMANA9 Espacios de medida - Aplicaciones (Medidas exteriores. Medida exterior AC de Lebesgue, Teorema de extensión de Carathéodory-Hahn, Teorema de completación de una medida. AA Construcción de la medida de Lebesgue, Existencia de conjuntos no Lebesgue medibl Espacios de medida - Aplicaciones (Medidas exteriores. Medida exterior AC de Lebesgue, Teorema de extensión de Carathéodory-Hahn, Teorema de completación de una medida. Construcción de la medida de AA Lebesgue, Existencia de conjuntos no Lebesgue medibl Funciones medibles - Definición y operaciones con funciones medibles. AC Funciones Borel y Lebesgue medibles Funciones medibles - Límite puntual de una sucesión de funciones medibles. Teorema de aproximación 3.0 5.0 3.0 Ejercicios fuera de clase, lecturas fuera de clase, búsqueda de información 4.0 Exposición oral (clase magistral), ejercicios dentro de clase, lecturas dentro de clase 3.0 Ejercicios fuera de clase, lecturas fuera de clase, búsqueda de información 5.0 AA 3.0 AC 5.0 AA 3.0 Funciones medibles - Definición y operaciones con funciones medibles. AC Funciones Borel y Lebesgue medibles, Teorema de Egoroff AA Integración sobre espacios de medida - Integral de funciones medibles no AC negativas. Desigualdad de Chebyshev AA SEMANA10 Integración sobre espacios de medida - Integral de funciones medibles no AC negativas. Desigualdad de Chebyshev AA SEMANA11 Integración sobre espacios de medida - Lema de Fatou y teorema de AC convergencia monótona para funciones medibles no AA negativas 5.0 3.0 5.0 3.0 5.0 3.0 5.0 3.0 SEMANA12 Integración sobre espacios de medida - Teorema de convergencia dominada AC de Lebesgue 5.0 AA 3.0 SEMANA13 Integración sobre espacios de medida producto AC 5.0 AA 3.0 SEMANA14 Espacio de funciones p-integrables Espacios seminormado y normado de AC funciones p-integrables 5.0 AA 3.0 AC 5.0 AA 3.0 AC 5.0 SEMANA15 Espacio de funciones p-integrables Propiedades de los espacios Lp SEMANA16 Espacio de funciones p-integrables Propiedades de los espacios Lp (completitud, densidad, reflexibidad, de clase Ejercicios fuera de clase, lecturas fuera de clase, búsqueda de información Exposición oral (clase magistral), ejercicios dentro de clase, lecturas dentro de clase Exposición oral (clase magistral), ejercicios dentro de clase, lecturas dentro de clase Ejercicios fuera de clase, lecturas fuera de clase, búsqueda de información Exposición oral (clase magistral), ejercicios dentro de clase, lecturas dentro de clase Ejercicios fuera de clase, lecturas fuera de clase, búsqueda de información Exposición oral (clase magistral), ejercicios dentro de clase, lecturas dentro de clase Ejercicios fuera de clase, lecturas fuera de clase, búsqueda de información Exposición oral (clase magistral), ejercicios dentro de clase, lecturas dentro de clase Ejercicios fuera de clase, lecturas fuera de clase, búsqueda de información Exposición oral (clase magistral), ejercicios dentro de clase, lecturas dentro de clase Ejercicios fuera de clase, lecturas fuera de clase, búsqueda de información Exposición oral (clase magistral), ejercicios dentro de clase, lecturas dentro de clase Ejercicios fuera de clase, lecturas fuera de clase, búsqueda de información Exposición oral (clase magistral), ejercicios dentro de clase, lecturas dentro de clase Ejercicios fuera de clase, lecturas fuera de clase, búsqueda de información Exposición oral (clase magistral), ejercicios dentro de clase, lecturas dentro de clase Ejercicios fuera de clase, lecturas fuera de clase, búsqueda de información Exposición oral (clase magistral), ejercicios dentro de clase, lecturas dentro de clase Ejercicios fuera de clase, lecturas fuera de clase, búsqueda de información Exposición oral (clase magistral), ejercicios dentro de clase, lecturas dentro de clase Ejercicios fuera de clase, lecturas fuera de clase, búsqueda de información Exposición oral (clase magistral), ejercicios dentro de clase, lecturas dentro de clase AA 3.0 Ejercicios fuera de clase, lecturas fuera de clase, búsqueda de información DOCENTE: ROSADO CORDOVA EMILIO JOSE, PARALELO: A, COMPONENTE : AP N° SEMANA 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 SEMANA1 Ejercicios SEMANA2 Ejercicios SEMANA3 Ejercicios SEMANA4 Ejercicios SEMANA5 Ejercicios SEMANA6 Ejercicios SEMANA7 Ejercicios SEMANA8 Ejercicios SEMANA9 Ejercicios SEMANA10 Ejercicios SEMANA11 Ejercicios SEMANA12 Ejercicios SEMANA13 Ejercicios SEMANA14 Ejercicios SEMANA15 Ejercicios SEMANA16 Ejercicios COMPONENTE DE APRENDIZAJE AP AP AP AP AP AP AP AP AP AP AP AP AP AP AP AP CONTENIDO HOR ACTIVIDADES DE APRENDIZAJE AS 1.0 Ejercicios 1.0 Ejercicios 1.0 Ejercicios 1.0 Ejercicios 1.0 Ejercicios 1.0 Ejercicios 1.0 Ejercicios 1.0 Ejercicios 1.0 Ejercicios 1.0 Ejercicios 1.0 Ejercicios 1.0 Ejercicios 1.0 Ejercicios 1.0 Ejercicios 1.0 Ejercicios 1.0 Ejercicios BIBLIOGRAFÍA BÁSICA: 1.-Chamorro, D. , 2010. Espacios de Lebesgue y de Lorentz... Lugar de publicación: París - Francia. EditorialAmarun BIBLIOGRAFÍA COMPLEMENTARIA: -Bartle, R. , 1995. The Elements of Integration and Lebesgue Measure... Lugar de publicación: USA. EditorialJohn Wiley & Sons METODOLOGÍA DE APRENDIZAJE DE LA ASIGNATURA DOCENTE: YANGARI SOSA MIGUEL ANGEL, PARALELO: A, COMPONENTE : AC Método de aprendizaje Clase magistral Recursos de aprendizaje Trabajos en grupo, lecturas Escenarios de aprendizaje Aula de clase DOCENTE: ROSADO CORDOVA EMILIO JOSE, PARALELO: A, COMPONENTE : AP Método de aprendizaje Clase magistral Recursos de aprendizaje Material de clase Escenarios de aprendizaje Aula de clase EVALUACIÓN IMPORTANTE: De acuerdo al Art. 80 del RRA la contribución de cada componente de evaluación no podrá exceder el 35% de la calificación del aporte ACTIVIDAD DE EVALUACIÓN Prueba Exposición Examen TIPO Formativa Formativa Sumativa APORTE 1 (%) 35.0 30.0 35.0 100.0 APORTE 2 (%) 35.0 30.0 35.0 100.0 HORARIO Y MECANISMOS DE TUTORÍAS: DOCENTE: YANGARI SOSA MIGUEL ANGEL, PARALELO: A, COMPONENTE: AC Horario (s) de tutorías Viernes de 9 a 10 Ubicación / mecanismo / herramienta de contacto Oficina del profesor de la materia DOCENTE: ROSADO CORDOVA EMILIO JOSE, PARALELO: A, COMPONENTE: AP Horario (s) de tutorías Bajo cita previa Ubicación / mecanismo / herramienta de contacto 0992722256 POLÍTICAS DE DESARROLLO DE LA ASIGNATURA DOCENTE: YANGARI SOSA MIGUEL ANGEL, PARALELO: A, COMPONENTE: AC La copia en un ejercicio será penalizada con la nota de cero en todo la evaluación Es obligatoria la asistencia a las clases, la inasistencia deberá ser justificada Se prohibe el uso de videos y fotos, con fines no académicos DOCENTE: ROSADO CORDOVA EMILIO JOSE, PARALELO: A, COMPONENTE: AP ADAPTACIONES CURRICULARES PARA ATENDER A ESTUDIANTES CON NECESIDADES EDUCATIVAS ESPECIALES: Metodologías de enseñanza-aprendizaje: Ninguna Ambientes de enseñanza-aprendizaje: Ninguna Métodos e instrumentos de evaluación: Ninguna UBICACIÓN: Espacio:E39-PB/E019