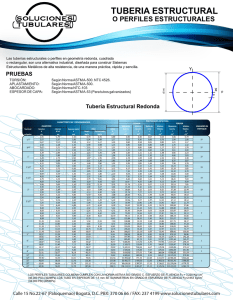
Introduccion-Al-Analisis-de-Esfuerzos-de-Tuberia

INTRODUCCION AL ANALISIS DE ESFUERZOS DE
TUBERIAS
Traduccion de: “ Introduction to pipe stress analysis “
Sam Kannappan, P.E.
Ingeniero
Tennessee Valley Authority
Knoxville, Tennessee
Realizado por: Benjamin Serratos ( Agosto 2008 )
Nota importante: El propósito de esta traducción es proporcionar una herramienta que
considero importante a los proyectistas e ingenieros de diseño de tuberías. Se realizó usando
los modismos y palabras que se usan regularmente en México, y en algunas partes el libro
original no es legible por lo que espero comentarios en la dirección mail [email protected].
Para realizar una fe de erratas en el original.
1
CONTENIDO
1
1.1
1.2
1.3
1.4
1.5
1.6
Análisis de esfuerzo de tubería.
Fuerzas y momentos en un sistema de tuberías
Cargas estáticas y dinámicas
Especificación de tubería.
Explicación de términos relacionados a soportes de tubería
El método de cantiléver guiado
Comparación de métodos simplificados de análisis
5
5
8
10
12
14
15
2
2.1
2.2
Diseño de componentes de presión
Calculo de grosor mínimo de pared de tubería
Refuerzo de conexiones de ramales soldados
21
21
27
3
3.1
3.2
3.3
3.4
3.5
Calculo del claro de tuberías
Limitaciones del claro
Frecuencia natural
Drenaje
Guía de espaciado para cargas de viento
Reglas de diseño para soportes de tubería
33
33
34
36
41
43
4
4.1
4.2
44
44
4.3
4.4
4.5
4.6
4.7
Códigos de tubería ANSI y códigos ASME
Presión interna y esfuerzos longitudinales
Requerimientos del código de tuberías para refinarías de petróleo
para un análisis formal
Momentos flexores en y fuera de plano
Factores de intensificación de esfuerzo
Efecto de la presión en los factores de intensificación de esfuerzos y flexibilidad
Esfuerzos en sistemas de tuberías
Resorte frio
5
5.1
5.2
5.3
5.4
Espiras y juntas de expansión
Espiras de expansión
Esfuerzos y cargas en espiras
Juntas de expansión
Tipos de juntas de expansión
72
72
75
81
83
47
49
50
59
63
66
2
5.5
Fuerzas de empuje de presión
85
6
6.1
6.2
6.3
Juntas bridadas
Nomenclatura
Momentos externos
Comparación de momentos reales y permisibles
90
90
91
92
7
7.1
7.2
Tuberías conectadas a equipo no rotatorio
Calculo de esfuerzos locales usando el boletín WRC 107
Tasa de resorte rotacional para recipientes cilíndricos
96
96
102
8
8.1
8.2
8.3
8.4
Tuberías conectadas a equipos rotatorios
Tuberías conectadas a turbinas de vapor
Tuberías conectadas a compresores centrífugos
Tuberías conectadas a bombas centrifugas
Método de cedencia en tuberías
106
106
110
110
113
9
9.1
9.2
9.3
9.4
9.5
9.6
9.7
9.8
9.9
9.10
9.11
Tópicos especiales
Válvulas
Análisis debido a fuerzas de reacción para válvulas de descarga
Tuberías de aluminio
Tuberías de aleación de cobre
Tuberías subterráneas
Diseño para presiones externas
Recipientes bajo presión externa
Sistema de tubería enchaquetada a presión
Unidades métricas
Comportamiento del material a temperaturas elevadas
Recubrimiento refractario
116
116
120
122
123
126
131
137
138
139
141
143
10
10.1
10.2
10.3
Código de componentes nucleares, ASME sección III
Cargas de diseño y limites de servicio
Flexibilidad y factores de intensificación de esfuerzos
Análisis para la evaluación de esfuerzos para tuberías clase 2
147
147
147
152
3
10.4
10.5
10.6
10.7
10.8
10.9
Apéndices
A1
A2
A3
A4
A5
Frecuencia natural
Sistemas de tuberías a ser analizadas
Sugerencias útiles en diseño de tuberías
Modelaje por computadora
Anclaje inicial y movimientos de soportes
Modelaje de elementos de tubería
154
155
156
157
158
160
Expansión térmica total para metales
Módulos de elasticidad para metales
Esfuerzos permisibles en tensión para materiales
Propiedades y pesos de tubería
Cálculos muestra para refuerzo de ramales
170
171-180
181-184
187-198
199-203
204
Anexos
Problemas resueltos
205
Índice
210
4
CAPITULO UNO
ANALISIS DE ESFUERZO DE TUBERIA
El análisis de esfuerzo de tubería provee la técnica necesaria para que los ingenieros diseñen sistemas de tubería sin
sobre esforzar o sobrecargar los componentes de tubería y equipo conectado. Los términos siguientes de mecánica
aplicada están aquí brevemente discutidos (no definidos) para familiarizar al ingeniero con ellos.
1.1
Fuerza
Momento
FUERZAS Y MOMENTOS EN SISTEMAS DE TUBERIA
La fuerza es una cantidad vectorial con la dirección y magnitud de los efectos de empuje
(compresión), jalón (tensión) o esfuerzo cortante.
Momento es una cantidad vectorial con la dirección y magnitud de los efectos de torsión y flexión.
Se discutirán mas tarde a detalle los momentos y fuerzas actuando sobre el sistema de tubería debido a diferentes
tipos de cargas, tales como expansión térmica y peso muerto.
El esfuerzo es la fuerza por unidad de área; este cambio en longitud dividido entre la longitud original es llamado
deformación.
Curva esfuerzo-deformación para materiales dúctiles y no dúctiles.
Para un material dúctil tal como el ASTM A53 grado B, la curva esfuerzo-flexión esta dada en la figura 1.1. La
variación de esfuerzos en el material con respecto a la deformación sigue una línea recta hasta que el limite
proporcional se alcanza. La ley de Hook define la pendiente como un modulo de elasticidad de Young E. El ultimo
esfuerzo tensil es la mas alta fuerza….
5
la curva en la cual algún tirón adicional causará deformaciones permanentes a los elementos bajo esfuerzo; el
esfuerzo permisible es el esfuerzo de cedencia dividido entre el factor de seguridad.
Figura 1.1. Típica curva esfuerzo-deformación para material dúctil ( ASTM A53 grado B )
Una curva típica para esfuerzo-deformación para un material no dúctil como el fierro fundido esta dado en la figura 1.2.El diagrama
esfuerzo-deformación para un material de tubería dado muestra las limitaciones en el esfuerzo para evitar la deformación o ruptura.
Figura 1.2. Típica curva esfuerzo-deformación para material no dúctil (Fierro fundido).
Materiales de tubería comunes
Se da a continuación (como referencia 1) una lista de materiales comunes de tubería bajo severas condiciones cíclicas:
Tubería para condiciones cíclicas severas .
Solo la siguiente tubería debiera ser usada bajo condiciones cíclicas severas.
( a ) Tubería de acero al carbón.
API 5L, sin costura
6
API 5L, SAW, Factor (E) 0.95 o mayor
API 5LX 42, sin costura
API 5LX 46, sin costura
API 5LX 52, sin costura
ASTM A 53, sin costura
ASTM A 106
ASTM A 333, sin costura
ASTM A 369
ASTM A 381, factor (E) 0.90 o mayor
ASTM A 524
ASTM A 671, factor (E) 0.90 o mayor
ASTM A 672, factor (E) 0.90 o mayor
ASTM A 691, factor (E) 0.90 o mas grande
(b)
Tubería de acero de baja y alta aleación
ASTM A 333, sin costura
ASTM A 335
ASTM A 369
ASTM A 426, factor (E) 0.90 o mayor
ASTM A 671, factor (E) 0.90 o mas grande
ASTM A 672, factor (E) 0.90 o mayor
ASTM A 691, factor (E) 0.90 o mayor
(c)
Tubería aleada de acero inoxidable
ASTM A 268, sin costura
ASTM A 312, sin costura
ASTM A 358, factor ( E ) 0.90 o mayor
ASTM A 376
ASTM A 430
ASTM A 451, factor ( E ) 0.90 o mayor
(d)
Tubería de cobre o aleaciones de cobre
ASTM B 42
ASTM B 466
(e)
Tubería de níquel o aleaciones de níquel
ASTM B 161
ASTM B 165
ASTM B 167
7
ASTM B 407
Tubería de aleación de aluminio
ASTM B 210, templado 0 y H 112
ASTM B 214, templado 0 y H 112
(f)
Para composición química y propiedades químicas de cada uno de los materiales de arriba, ver Estándares ASTM ( referencia 2 ).
Materiales de tubería especiales incluyen inconel, hastelloy, zirconio y aleaciones de aluminio. La selección de un material especifico
depende de las propiedades de corrosión y temperatura del proceso. El dimensionamiento de la tubería depende del volumen de flujo
con la mínima fricción de flujo ( referencia 8 ).
1.2
Cargas estáticas y dinámicas.
Las cargas afectando el sistema de tubería pueden ser clasificadas como primarias y secundarias. La carga primaria ocurre de cargas
sostenidas como el peso muerto. Las cargas primarias son llamadas cargas no auto limitantes. Un ejemplo de carga secundaria (auto
limitante) es la carga de expansión térmica. A causa de que códigos de tubería diferentes definen el criterio de calificación de tubería
en caminos ligeramente diferentes, cada código será encarado separadamente mas tarde.
Las cargas estáticas incluyen:
1.
2.
3.
4.
Efecto peso ( cargas vivas y cargas muertas )
Efectos de expansión y contracción térmica.
Efectos de soporte, anclaje y movimientos terminales.
Cargas de presión interna y externa.
Las cargas vivas bajo el efecto del peso incluyen peso del contenido, nieve, y cargas de hielo. Las cargas muertas consisten de pesos
de válvulas de tubería, bridas, aislamiento, y otras cargas permanentes sobrepuestas.
Las cargas dinámicas incluyen:
1.
2.
3.
4.
5.
Fuerzas de impacto.
Viento.
Cargas sísmicas ( terremotos )
Vibración.
Cargas de descarga.
Propiedades del material de tubería.
8
Los efectos termales incluyen: cargas térmicas que surgen cuando expansión o contracción térmica libre es estorbada por soportes o
anclajes, cargas debidas a gradientes de temperatura en paredes de tubería delgada, y cargas debidas a la diferencia en coeficientes
térmicos de materiales en tuberías enchaquetadas. El coeficiente de expansión lineal de un solido esta definido como el incremento
de longitud en una unidad de longitud para el cambio de temperatura de un grado F; la unidad es micro pulgadas por pulgada por
°F. La unidad para el coeficiente medio de expansión térmica entre 70 °F ( temperatura de instalación ) y la temperatura dada es
proporcionada como pulgadas de expansión por 100 pies de tubería en la tabla A1 del apéndice ( Los valores son del código de
tubería ASME B31.3 ). Para convertir de pulg/pulg/|F a pulg /100 pies, se puede usar la siguiente relación:
Coeficiente expansión(pulg/100pies)=(coef)x 12 x 100 ( temperatura de diseño – temperatura de instalación)
( 1.1.)
Modulo de Young o modulo de elasticidad E es una unidad de esfuerzo dividida entre una unidad de deformación. Para la mayoría de
materiales estructurales el modulo de elasticidad es el mismo para compresión que para tensión. El valor de E decrece con el
incremento de temperatura. La tabla A2 del apéndice da valores de E para materiales de tubería para el rango normal de temperatura.
La razón de unidad de contracción lateral entre la unidad de elongación se llama razón de Poisson. Los códigos permiten un valor de
0.3 para ser usados a todas las temperaturas para todos los metales.
Tabla 1.1. Razón de Poisson y densidades para materiales de tubería
Tipo de material
Densidad ( lb /
Acero al carbón con 0.3 % de carbón o menos
Aceros austeniticos ( aceros inoxidables )
Aleaciones intermedias de acero 5% Cr Mo-9% Cr Mo
Bronce ( 66% Cu-34 % Zn )
Aleaciones de aluminio
Razon de Poisson
0.283
0.288
0.288
0.292
0.283
0.292
0.316
0.331
0.100
0.334
La tabla 1.1 da razones de Poisson y densidades para materiales comunes de tubería.
Gravedad especifica : La gravedad especifica de un solido o liquido es la razón de la masa de un igual volumen de agua a la misma
temperatura estándar ( los físicos usan 39 °F y los ingenieros 60 |F ). La gravedad especifica de gases es
generalmente expresada en términos de hidrogeno o aire. Es un numero sin unidad.
Densidad:
La densidad ρ es la masa por unidad de volumen del fluido; la unidad es lb/
.
Peso especifica:
El peso especifico ω es el peso por unidad de volumen; la interrelación de densidad y gravedad especifica es
ω = gρ , donde g es la aceleración debido a la gravedad.
Ejemplos
1. Hallar la expansión térmica lineal ( pulg/100pies ) entre 70 y 392 °F para acero al carbón. El coeficiente para 375 °F = 2.48
pulg/100 pies ( valores del apéndice A1 ).
Coeficiente para 400 °F = 2.7 pulg/100pies
9
Diferencia por grado en expansión = ( 2.7 - 2.48 )/25 = 0.0088
Por interpolación, la expansión para 392 °F = 2.48 + (392- 375)(0.0088) = 2.63 pulg/100pies
2. Hallar el modulo de elasticidad para el acero austenitico a : (a) -200 °F, (b) 70 °F y (c) 625 °F.
E a 200 °F = 29.9 x 10 psi ( leer en el apéndice tabla A2 )
E a 70 °F = 28.3 x 10 psi
E para 625 °F seria la interpolación entre los valores de 600 °F y 700 °F
E para 600°F = 25.4 x 10 psi
E para 700°F = 24.8 x 10 psi
E para 625°F es 25.4 - 25((25.4 - 24.8)/100) = 25.4 - 0.15 = 25.25 x 10 psi
Note que los valores de E decrecen con el incremento en la temperatura. Los valores menores del modulo de Young significan que la
se permite para el calculo de momentos y fuerzas en boquillas de equipos.
flexibilidad es mas alta. El uso del modulo caliente
Sin embargo, el valor mas alto ( a 70 °F o temperatura de instalación ) debe ser usado en calculo de esfuerzos.
1.3
Especificación de tuberías.
La especificación de tubería se redacta para cada uno de los servicios como vapor, aire, oxigeno, cáusticos, etc. La especificación
contiene información acerca de material de tubería, grosor, válvulas recomendadas, bridas, conexiones de ramal , y conexiones de
instrumentos. La figura 1.3 muestra una especificación para servicio caustico.
Ejemplo
Un tubería de 8”Ø necesita un tubo con un grosor de cedula 80 ( el cual da 1/8” de corrosión permisible y una presión interna
máxima de 200 psig a 150 °F )sin costura con terminadas biseladas A53 grado B. La válvula de globo usada es Crane 351 ( referencia
1 en el capitulo 9); Las bridas son de 150 psi de rango de presión del tipo de cuello soldadle y deslizables, el material de la brida es
A105 ( según estándar ANSI B16.5 ). El requerimiento de ramal ( aquí weldolet o te )se dan en la tabla de conexiones; para un cabezal
de 8”Ø y un ramal de 3”Ø, se requiere un weldolet para dar la presión interna. Las condiciones de temperatura y presión en la
tubería debieran generalmente estar dentro ( en el interior de la línea achurada ) de la curva de presión-temperatura dadas en la
especificación.
Válvulas
Diámetro
pulgadas
½
¾
1
1½
2
3
4
6
8
10
Tubería
Ced 160 sin
costura
ASTM-A106 Gr B
Ced 80
Con estremos
Biselados
ASTM A53
Grado B
Sin cost
Compuerta,
Bola ,macho
V - BOCB 125 psi
Roscada
Toda acero
Crane 484½
V BOCC
125 psi
Cara plana
Toda fierro
Crane 475½
Conexiones ramal
Globo
Retención
V-IGHT 150 psi
Roscada
Toda acero
Crane 355½
V - BGHU
125 psi
Cara plana
Toda fierro
Crane 351½
V - )CNY
1000 psi
MY
Crane 346½
V - BCHZ
125 psi
Cara plana
Toda fierro
Crane 373½
Juntas
mecánicas
300 psi roscada
Unión Con empaque
asientos acero
Accesorios
Reducciones
300 psi
MI roscada
Te reductora
roscada
Brida 150 # Cara
Realzada ASTM A105
Cuello soldable o
deslizable excepto
En accesorios ver
nota 1
Ced 80
Soldables
Sin costura
ASTM A234
1½” y mas
Pequeñas
Thredolet 3000#
2” y mayores
Ver tabla
inferior
Tamaño
completo
Te recta
roscada
Como se
muestra
en tabla
inferior
tamaño
½
¾
1
1½
2
3
4
6
8
10
10
Flexibilidad
Los sistemas de tuberías debieran tener suficiente flexibilidad, de manera tal que la expansión térmica, o la contracción, ó los
movimientos de soportes o puntos terminales, no causarán:
1.
Falla de tubería o soporte desde sobreesfuerzo ó fatiga
2.
Fuga en las juntas
3.
Esfuerzos perjudiciales ó distorsiones dañinas en la tubería , ó equipo conectado( bombas, recipientes, válvulas,
etc) resultado de un empuje o tracción ó momentos en la tubería excesivos en la tubería
11
La figura 1.4 muestra ejemplos de tuberías tiesas y flexibles. Cuando una tubería esta sujeta a cambios de temperatura y si la tubería
no esta restringida a la expansión, ningún esfuerzo se desarrolla y la tubería solo se expande y se contrae. Cuando la tubería esta
restringida, se crean esfuerzos y fuerzas de considerable magnitud. Por ejemplo, En una refinería cerca de Houston, Texas, donde dos
restricciones estuvieron presentes en una línea de vapor recta ( ver figura 1.13 ), ocasionó que un soporte largo se doblara y la falla
de un tubo en el área soldada de un pie de tubería.
Figura 1.4 Tubería tiesa y flexible.
La fuerza térmica que se desarrolla cuando ambos extremos de una tubería están restringidos es enorme y es también independiente
de la longitud de la tubería.
Fuerza térmica = E ( tirón debido a la expansión ) ( área metálica )
( 1.2. )
Ejemplo
Cal cular la fuerza desarrollada en una tubería de 10” cedula 40 acero al carbón A53 grado B sujeto a 200°F desde una temperatura
de instalación de 70 °F.
El área metálica de un tubo de 10” ced 40 es 11.9 ( Apéndice Tabla A4 )
El coeficiente de expansión a 200°F es 0.99 pulg/100 pies ( Apéndice tabla A1 )
E = 27.9 x 10 psi
( Apéndice Tabla A2 )
12
F = EaA = 27.9 x 10 x
.
x 11.9 {unidades :
(
)
= libras
F = 273 908 libras
El arreglo de un sistema de tuberías provee flexibilidad inherente a través de los cambios de dirección. La tubería rígida que se
muestra en la figura 1.4 puede hacerse mas flexible por diferentes caminos. En la figura 1.5 se muestra la inclusión de una espira de
expansión si existe espacio; Se le puede colocar una junta de expansión ( fig 1.6) ( ver ecuación 5.4 para calculo de fuerzas de
empuje), o el equipo puede ser girado 90 grados para así forzar que la pierna absorba la expansión, como se muestra en la figura 1.7.
Cuando un sistema de tubería carece en el arreglo de cambios de dirección, el ingeniero debiera considerar sumar flexibilidad por
uno o mas de los siguientes medios: codos, espiras o desplazamientos, juntas giratorias, tubería corrugada, juntas de expansión de la
de tipo fuelle o deslizante; u otros tipos de aditamentos permitiendo movimientos angulares, rotativos o axiales. Las juntas de
expansión y las espiras de expansión se discutirán a detalle en el capitulo 5 .
1.4
Explicación de términos relacionados con soportes de tubería.
Anclaje
Un empotramiento rígido que provee sustancialmente completa fijación para las tres traslaciones y rotaciones sobre
los tres ejes de referencia. Se asume un gran numero en el orden de 10 libras/pulg para el atiesamiento
traslacional en los programas de computación digital para simular le fijación. Los detalles de un anclaje estructural
se pueden obtener de cada uno de los estándares de las compañías de soportes de tubería.
Abrazadera
Un artificio proyectado primeramente para resistir desplazamiento de la tubería debido a la acción de cualesquiera
otras fuerzas que las debidas a la expansión térmica o gravedad. Notar que con esta definición, un artificio de
amortiguamiento se clasifica como un tipo de abrazadera.
Soporte de esfuerzo constante
Un soporte capaz de aplicar un fuerza relativamente constante en cualquier desplazamiento
dentro de un rango de operación útil ( por ejemplo, contrapeso o artefacto con resorte compensante).
Artificio de amortiguamiento
Un amortiguador u otro artefacto de fricción que incrementa el amortiguamiento de un sistema,
ofreciendo alta resistencia contra desplazamientos rápidos causados por cargas dinámicas mientras que permiten
esencialmente libre movimiento bajo desplazamientos aplicados muy gradualmente ( por ejemplo, amortiguador ).
Colgante
Un soporte por medio de la cual una tubería esta suspendida de una estructura.
Tope limite
Un artefacto que restringe el movimiento traslacional a una limitada cantidad a lo largo de un eje definido.
Paralelamente se pueden colocar topes de doble acción, topes limites de dos ejes y similares.
Soporte elástico Un soporte que incluye uno o mas miembros fuertemente elásticos ( resortes ).
Soporte portador o deslizante
Un artificio que provee soporte debajo de la tubería pero no oponiendo otra resistencia que la
fricción al movimiento horizontal.
Fijación
Cualquier artificio que previene, resiste o limita el libre movimiento de la tubería.
Soporte rígido (solido) Un soporte que provee fijación en al menos una dirección, la cual sea comparable a la de la tubería.
Limitador
Un artefacto que permite la rotación pero previene el movimiento de traslación en al menos una dirección a lo largo
de cualquier eje. Si la prevención es en ambas direcciones a lo largo de un eje, se debe usar el termino de limitador
de doble acción. El limitador se conoce también como parachoques.
13
Soporte
Un artefacto usado específicamente para sostener una porción del peso del sistema de tubería mas cualesquiera
cargas verticales sobrepuestas.
Limitador de dos ejes
Un artefacto que previene el movimiento de traslación en una dirección a lo largo de dos ejes.
Una vez que el análisis completo del sistema de tubería ( peso, térmico mas presión, y térmico mas presión mas peso ) se han
realizado, las modificaciones de soporte se pueden realizar fácilmente.
Cuando una línea de tubería se mueve como un resultado de la expansión térmica, es necesario que se proporcionen colgantes
flexibles que proporcionen el soporte al sistema de tubería a través de su ciclo térmico. Se emplean generalmente tres tipos de
colgantes:
1 Soporte rígido o colgante de barra el cual supuestamente previene cualquier movimiento a lo largo del eje del colgante; los
colgantes de barra se usan cuando las deflexiones térmicas libres son lo bastante pequeñas para que su sujeción de los
movimientos no produzcan reacciones excesivas en el sistema de tuberías.
2 Soportes variables o colgantes de resorte proporcionan una fuerza soportante igual a la carga caliente ( referencia 6 )
mientras que permite la deflexión.
3 Soporte colgante o colgante de esfuerzo constante es ese que provee una fuerza esencialmente constante a través del ciclo
térmico. Idealmente, los colgantes de esfuerzo constante no deben restringir el libre movimiento del sistema y por esto no
incrementan los esfuerzos de la tubería.
1.5 Método del cantiléver guiado
Uno de los métodos simplificados usados en el diseño de tubería es conocido como el método del cantiléver guiado, a causa de
que se asume que ocurren en un sistema de un plano bajo la aproximación guiada del cantiléver, como se muestra en la figura
1.8.la capacidad de deflexión de un cantiléver bajo esta suposición puede ser dado por la ecuación 1.3 ( referencia 3 ):
∆=
( 1.3 )
Donde:
∆ = Deflexión permisible , pulg.
= Rango de esfuerzo permisible, psi ( dado por ecuación 4.1 )
L = Longitud de pierna necesaria para absorber la expansión, pies.
= Diametro exterior de la tubería. Pulg.
Las limitaciones del método de cantiléver guiado son:
1. El sistema solo tiene dos puntos terminales y esta compuesto de piernas rectas de una tubería, con tamaño y grosor
uniforme en intersecciones a escuadra.
2. Todas las piernas son paralelas a los ejes de coordenadas.
3. La expansión térmica es absorbida solo por las piernas en una dirección perpendicular.
4. La cantidad de expansión térmica que una pierna dada puede absorber es inversamente proporcional a su rigidez. A causa de
que las piernas son de una sección transversal idéntica, su rigidez variará de acuerdo al valor inverso del cubo de sus
longitudes.
14
5. En la acomodación de la expansión térmica, las piernas actúan como un cantiléver guiado, esto es, ellas están sujetas bajo
los movimientos terminales; sin embargo, No se permite la rotación en las terminales, como se muestra en la figura 1.8.
Figura 1.8 Aproximación del cantiléver guiado.
Como un refinamiento adicional de este método, un factor de corrección puede ser usado que permite la reducción del momento
de flexión, debido a la rotación de la pierna adyacente a la que consideramos ( referencia 3 ).
Figura 1.9
Anclaje con movimiento inicial.
Ejemplo
Calcular la pierna L requerida para el problema con dos anclajes y fuerza P dados en la figura 1.9.
Diámetro exterior de tubo = 4½” ;
grosor = 0.237 pulg
Coeficiente de expansión = 4”/100pies
= 15 000 psi
Rango de esfuerzo =
Modulo frio = E = 27.9 x 10 psi
Deflexión = ∆ = 1½ + 20(4/100) = 2.3 pulg
Rearreglando la ecuación 1.3 ( método del cantiléver guiado ):
L=
∆
.
=
Esfuerzo de flexión =
=
Radio medio = r = ½(
.
.
.
= 20.03 pies
=
.
.
) = 2.13 pulg
15
( grosor ) = π 2.13 (0.237) = 3.38
Modulo de sección = Z = π
Fuerza P =
=
.
.
= 421.8 libras
1.6 Comparación de los métodos simplificados de análisis.
Se comparan aquí los resultados obtenidos de otros métodos simplificados y el análisis de tuberías ayudado por computadoras
digitales: Sin embargo cada uno de los métodos no esta completamente explicado a causa de que las referencias dan una detallada
explicación y ellas también necesitan de cartas y graficas para su solución. Para comprender las diferencias entre cada uno de los
métodos, los resultados para tres problemas para un rango de diámetros de 6” - 24” se presentan en la tabla 1.3 ( referencia 4 ).
Métodos
1.
2.
3.
4.
5.
Tube turns ( referencia 5 )
ITT Grinell ( referencia 6 )
M.W. Kellogg ( referencia 3 )
Solución de computadora digital incluyendo factores de flexibilidad ( referencia 7 )
Solución de computadora digital usando aproximaciones cuadráticas ( no incluyen flexibilidad de flexión )
La tabla 1.2 incluye el rango de diámetros (6”-24”), grosor de pared, y el momento de inercia I usado en los cálculos. La tabla 1.3
muestra la configuración de una Espira U ( junta de expansión, una con perfil L y otra con perfil Z. El máximo esfuerzo de flexión
esta dado para cada uno de los métodos.
Tabla 1.2
Tamaños de tubería usados en la comparación de métodos simplificados.
16
Tabla 1.3 Comparación de esfuerzos de flexión máximos de diferentes métodos, psi.
La figura 1.10 muestra la variación de esfuerzos de flexión contra el área de momentos de inercia I para la espira. Aquí I fue
seleccionada en lugar del diámetro a cusa de que I también incluye el efecto del grosor de pared. Como podemos ver el método
Grinell da los resultados conservadores mucho mas altos. Las juntas de expansión se discuten adicionalmente en el capitulo 5.
Figura 1.10 Esfuerzos de flexión en espiras simétricas.
17
La figura 1.11 muestra la variación de los esfuerzos de flexión para un perfil L. El método Kellogg nos da los valores mas altos de
esfuerzo. La figura 1.12 demuestra la variación de esfuerzos de flexión con momentos de inercia para el perfil Z. La solución por
computadora digital usando el programa EZFLEX nos da los números menores, lo cual es entendible a causa de que los otros
métodos son obligados a ser conservadores. El método Kellogg esta discutido en detalle en el capitulo 5 ( ecuaciones 5.2 y 5.3 ).
Figura 1.11 Esfuerzos de flexión en una tubería de perfil “ L “.
Figura 1.12 Esfuerzos de flexión en una tubería de perfil “ Z “.
18
1.
(a)
(b)
(c)
2.
(a )
(b)
3.
4.
Ejercicios
Hallar la expansión total para una tubería de acero de aleación intermedia ( 5Cr Mo a 9 Cr Mo ) a
temperaturas de (1) -55°F, (2) 431 °F, (3) 1572 |F. Si la temperatura dada esta fuera del rango del
material, sugerir un material apropiado para esa temperatura. Considerar una longitud de 120 pies.
Hallar los siguientes datos para aceros austeniticos a la temperatura de operación:
1.
Modulo de Young.
2.
Razón de Poisson.
3.
Densidad.
Calcular la elongación total en 132 pies de tubería hecha de acero al carbón sujeta a 645 °F.
Hallar los valores E para acero de bajo cromo a 115°F, 70 °F, y 800°F.Explicar el efecto de la
temperatura sobre los valores E.
Hallar los esfuerzos frio y caliente para tubería ASTM A53 grado B a 70°F y 625°F.
Calcular las fuerzas térmicas desarrolladas en la tubería que se encuentra fija en ambas terminales como se
muestra en la figura 1.13. Esta consiste de un tubo de 8”Ø cedula 40 de acero al carbón con una
temperatura de operación de 300°F. Usar la ecuación 1.2.
a = coeficiente de expansión térmica a 320°F = 1.82 pulg/100pies.
Figura 1.13 Fuerza térmica.
Calcular los esfuerzos del arrglo de la figura 1.14. Este consiste de un tubo de 10”Ø ced 40, acero al carbón
A53 grado B a 500°F.
= 20 000 psi
= 17 250 psi
Figura 1.14
tuberia de piernas desiguales con perfil “ L “.
19
5.
Calcular la pierna L necesitada en la figura 1.15. La cual es una tubería de 10”Ø ced 40 acero al carbón con
material A53 grado B el cual tiene una temperatura de 200°F. Los esfuerzos admisibles son = =
20 000 psi.
Figura 1.15
6.
Tuberia con perfil “ Z “ con movimientos iniciales de anclaje.
En el arreglo mostrado en la figura 1.16, dos boquillas de equipo tienen movimiento térmico. ¿ cual será la
longitud L ?. La tubería de acero al carbón tiene un diámetro nominal (Ø) 8” y a= 1.82 pulg/100pies.
= 18 000 psi
7.
Dos recipientes están conectados por tubería amo se ve en la figura 1.17. ¿ Cual es la longitud requerida para
la pierna ?,¿ Cual es la fuerza y el momento ? Para una tubería de 6”Ø de acero al carbonA53 grado B;la
expansión lineal es 3” , el rango de esfuerzo permisible es = 28 000 psi.
Figura 1.17
8.
E = 27.9 x 10 psi.
Calculo de la fuerza y momento en el anclaje.
Como se muestra en la figura 1.18, un recipiente tiene una temperatura promedio de operación de 500°F;
con una línea que viene a la boquilla del recipiente desde un equipo. ¿ cual debiera ser la longitud L ? Es
20
una tubería de 12”Ø de acero A53 grado B.
= 20 000 psi y
= 16 350 psi. ( en el caso practico la Lesta limitada
por la altura de la torre.
Referencias
1.
2.
3.
4.
5.
6.
7.
8.
ANSI/ASME B31.3-1980 Chemical plant and Refinery piping..
ASTM Annual Book of ASTM Standars
Diferent parts for different materials.
M.W. Kellog.
Design of piping systems. New York.
Extrems, Fernando and S. Kannappan. “ Comparison of results from different simplified methods with digital computer
calculatios “
Tbe turns Division of Chemetron Corp. “ Piping Engineering.Line expansion and flexibility “.
ITT Grinnell Industrial Piping. “Piping design and Engineering”
EZFLEX Piping flexibility Analysis Program.
Crane Company. “ Flow of fluids”.
21
CAPITULO 2
DISEÑO DE COMPONENTES DE PRESION
2.1
CALCULO DE GROSOR DE PARED MINIMA DE UNA TUBERIA.
Lo códigos de tubería requieren que el grosor mínimo , incluyendo la tolerancia para esfuerzos mecanicos, no
deberían ser menores que el grosor calculado usando la ecuación 2.1.
=
donde:
( 2.1)
= Grosor mínimo de pared requerido, pulg.
t = Grosor de diseño de presión, pulg.
P = Presión interna, psig
= Diámetro exterior de tubería,pulg.
S = Esfuerzo permisible a la temperatura de diseño ( conocido como esfuerzo caliente )psi
( ver apéndice tabla A3 )
A = Tolerancia, grosor adicional que se provee para material que va a ser removido por roscado,
corrosión, o tolerancia por erosión; la tolerancia de manufactureros (MT) debe ser considerada.
Y = Coeficiente que se toma en cuenta de las propiedades del material y temperatura de diseño, para
t< , los valores de Y se dan en la tabla 2.1. Para temperaturas debajo de 900°F, 0.4 puede ser
asumida.
Y=
si t≥
(2.2a)
donde: d = Diámetro interior = - 2t
= Factor de calidad que es el producto del factor de calidad de fundición , el factor de calidad de la junta
factor de calidad del grado estructural cuando se aplican. Los valores de en el rango de 0.85 a 1.0
, y el
22
dependiendo del método usado para examinar la calidad de fundición ( ver tabla 2.2a ). Los valores de con rangos
de 0.6 a 1.0 ( dados en la tabla 2.2b ) y depende del tipo de soladura. Los valores de pueden ser asumidos como
0.92.
=
( 2.2b )
Tabla 2.1 Valores de coeficientes Y a ser usados en la ecuación 2.1.
Referencia ( ASME/ANSI B31.3-2004, tabla 304.1.1 )
Tabla 2.2a Factor incrementado de calidad de fundición .
Referencia ( ASME/ANSI B31.3-2004, tabla 302.3.3c )
23
Tabla 2.2b
Factor de calidad de junta soldada para costura recta y espiral longitudinal.
Referencia ( ASME/ANSI B31.3-2004, tabla 302.3.4 )
Ejemplo
Calcular el mínimo grosor de pared permisible para una tubería de 10”Ø bajo 350 psi y 650°F; el material es acero al carbón ASTM
A106 grado B, la corrosión permisible es 0.05 pulg y la tolerancia del molino (MT) es 12½%
Grosor
S=
=
(2.1.)
= 10.75
= 1.0 para tubería sin costura.
P = 350 psig
= esfuerzo permisible caliente ( tensil ) para A106 grado B = 17 000 psi ( ver apéndice A3 )
24
Y = 0.4 ( a causa de que la temperatura es menor a 900°F )
.
=
0.05
.
Grosor nominal =
.
=
0.144 pulg
.
=0.1648
.
Del manufacturero y la información de propiedades de sección de tubería, ( ver apéndice A4 ) un tubo de 10”Ø ced 20 esta
seleccionado con un grosor de pared de O.25 pulg. Para tuberías bajo presión externa ver ecuaciones 9.10 a 913.
Ecuaciones alternas para calcular grosor de pared.
Mirando de nuevo la ecuación 2.1 , vemos que:
=
( 2.1)
donde t es el grosor de presión de diseño en pulgadas.
Las ecuaciones 2.3 y 2.4 ( Ecuación de Lamé ) pueden también ser usarse para calcular t :
t=
(2.3)
(
t=
Las ecuaciones 2.1, 2.3 y 2.4 son validas para t<
Las tuberías con t ≥
(2.4)
(tubería delgada).
(tubería de pared delgada) o P/S
>0.385 requiere tomaren cuenta especial consideración en diseño y
factores de material, tales como teoría de falla, fatiga y esfuerzos térmicos ( referencia 1 ).
Presión de trabajo permisible.
La presión de trabajo permisible de una tubería puede ser determinada por la ecuación 2.5 :
P=
S
(2.5)
Donde t = grosor de pared especificado o grosor de pared real en pulgadas.
25
Para curvas el grosor mínimo de pared después de el doblado no debiera ser menor que el mínimo requerido para la tubería recta.
½
El grosor de presión de diseño t para tapas ciegas permanentes esta dado por la ecuación:
=
+A
Donde = diámetro interior del empaque, o cara plana o realzada de las bridas, o diámetro de paso de una o-ring y bridas
completas, todas ellas en pulgadas.
Presión de prueba
La presión de prueba hidrostática en cualquier punto del sistema debiera de ser no menor de 1½ veces la presión de diseño. Para
temperaturas arriba de 650°F, la presión mínima de prueba esta dada por :
= 1.5 (
)(presión de diseño)
(2.7)
= esfuerzo permisible a 650°F ( a 650°F )( ver apéndice tabla A3 )
S = Esfuerzo permisible a la temperatura de diseño ( a temperatura de diseño ).
Presiones permisibles en codos fragmentados.
*codos fragmentados * ( del ASME/ ANSI B.31.3-2004 sección 304.2.3)
Una desplazamiento de 3 grados o menos ( ángulo a en la figura 2.2 ) no requiere consideraciones de diseño en un codo
fragmentado. Los métodos aceptables para el diseño de presión de codos fragmentados simples o múltiples están dados en los incisos
(a) y (b).
Figura 2.1. Nomenclatura para codos fragmentados.
26
La siguiente nomenclatura se usa en las ecuaciones 2.8ª, 2.8b y 2.8c para el diseño a presión de codos fragmentados:
c = corrosión permisible.
= Máxima presión interna permisible para codos fragmentados.
= radio medio de tubería usando pared nominal T.
= Radio efectivo del codo fragmentado, definida como la distancia mas corta del centro de tubería a la intersección de
los planos de las juntas de los fragmentos adyacentes.
= Factor de calidad ( ver ecuación 2.2b )
S = Esfuerzo permisible a la temperatura de diseño, psi.
T = Grosor de pared de tubería ( medido o mínimo por especificación de compra )
Θ = Angulo de corte del segmento, grados.
a = Angulo de cambio de dirección en la junta fragmentada = 2Θ.
Para cumplir con este código, el valor de
no deberá ser menor que el dado por la ecuación 2.9:
=
+
( 2.9 )
tiene los siguientes valores empíricos ( no validos en unidades SI ):
Donde
Valor de ( T - c ), pulg
≤ 0.5
0.5 < ( T - c ) < 0.88
≥ 0.88
(a)
Codos fragmentados múltiples:
2
3
(b)
1.17
La máxima presión interna permisible debiera ser el valor menor calculado de las
ecuaciones 2.8 a y 2.8b. Estas ecuaciones no son aplicables cuando Θ excede a 2.5°.
=
=
Valor de
1.0
2(T-c)
.
(
.
( 2.8a )
( 2.8b )
Codos fragmentados simples ( o con ampliamente espaciados cortes ).
1.
2.
La máxima presión interna permisible para un codo simple fragmentado con un ángulo Θ no mayor que 22.5 °
debe ser calculado por la ecuación 2.8a.
La máxima presión interna permisible para un codo fragmentado simple con un ángulo Θ mayor que 22.5° debe
ser calculado por la ecuación 2.8c:
27
=
( 2.8c )
.
Ver el capitulo 4 para discusiones adicionales sobre codos fragmentados.
Ejemplo
Calcular la máxima presión interna permisible para el codo fragmentado múltiple, el grosor de placa es ½”. La corrosión permisible
es 0. La tolerancia del manufacturero es 0.01”. El diámetro exterior del codo fragmentado es 36”.
Para ver codo fragmentado de dos soldaduras fig 2.1.
.
Θ= =
= 11.25 °
El radio medio de la tubería = 35.5/2 = 17.75°
El material consiste de acero inoxidable A312 TP 304 H; la temperatura ES 1 310°F.
El esfuerzo caliente permisible es = S = 3 060 psi ( del apéndice Tabla A3 ).
Interpolando entre = 3 700 psi para 1300 °F y = 2 900 psi para 1350 °F. El radio de doblez es
Usando la ecuación 2.8a la presión permisible es
=
=
( 2.8a )
.
.
.
.
[
.
.
.
= 54 “ ( ver tabla 4.4 )
.
.
.
.
.
.
= 58 psig
Usando la ecuación 2.8b, la presión permisible es:
=
(
=
.
.
( 2.8b )
.
(
.
.
.
) =67.86 psig
La máxima presión permisible para el codo fragmentado de los valores calculados anteriormente es 58.6 psig .
2.2
Refuerzos para conexiones de ramales soldados
Cuando se corta un agujero en una tubería sujeta a presión interna, el disco del material que normalmente estaría conduciendo los
esfuerzos de tensión en la dirección del anillo son removidos y se debe proveer una vía alterna estos esfuerzos. Para alcanzar esto, se
usa una aproximación simplificada de área de remplazo o compensación. Este método provee material de refuerzo adicional, el
cual esta dentro de una distancia especifica de la orilla del agujero, igual al área del material removido. El refuerzo en las
28
intersecciones de ramal también son ocasionalmente necesarias para distribuir los esfuerzos incrementándose por las cargas de la
tubería. Ver los factores de intensificación de esfuerzos (SIF) en el capitulo 4 para la reducción del valor calculado del SIF cuando se
aplicaron los refuerzos. El requerimiento de refuerzo para presión interna generalmente están definidas en la especificación de
tubería del proyecto. Refuerzo adicional puede ser necesario para cargas de tubería.
Figura 2.2
Nomenclatura de conexiones de ramal
( ASME/ANSI B31.3-2004)
La figura 2.2 muestra una conexión ramal que sale de una tubería ( reproducida del código B31.3). Los requerimientos de otros
códigos es similar. Varios problemas solucionados están dados en el apéndice H los cuales provienen del código B31.3-2004.
(a)
Nomenclatura.
La nomenclatura en la figura anterior que se usa en el diseño a presión de conexiones de
ramal soldadas; esta indicada en la figura 2.2 donde nos muestra detalles de construcción o soldadura.
Algunos de los términos
definidos en el apéndice J están sujetos a definiciones adicionales o variaciones, como sigue:
b = Subíndice refiriéndose al ramal.
= Longitud efectiva removida de la tubería para el ramal. Para intersecciones de ramal donde el ramal
la apertura es una proyección del diámetro interior tubería ramal ( por ejemplo, ramal fabricado
tubería-tuberia)
= [ - 2 ( - c ) ] / sen β
= “ radio medio” de la zona de refuerzo = , ó
( - c) + ( - c ) + /2 , cualquiera que sea mayor, pero
en ningún caso mayor que .
H = Subíndice refiriéndose al cabezal o tubería principal.
= Altura de la zona de refuerzo fuera de donde corre el cabezal = 2.5 ( - c ) ó ( - c), cualquiera sea menor.
29
=
Grosor de tubería ramal ( medida o mínimo por especificación de compra ) excepto para accesorios de conexión de
y
es el grosor del barril de
ramal. Para tales conexiones el valor de para usarse en el calculo de ,
refuerzo ( mínimo según especificación de compra ) previendo que el grosor del barril sea uniforme (ver figura a
continuación) y se extienda al menos al limite de ( ver fig 2.2 )
a) sin refuerzo.
b) con refuerzo
c) salida angulada sin refuerzo
Conexiones típicas soldadas de ramal
Nota general:
Estos bocetos muestran detalles de soldadura mínimos. Las soldaduras pueden ser más grandes que las mostradas.
Detalles aceptables para uniones soldadas
= Grosor mínimo del anillo de refuerzo o silleta hecho de la tubería ( usar el grosor nominal si se usa placa ), = 0, si
no hay silleta o anillo de refuerzo .
t = Grosor de presión de diseño de tubería, de acuerdo a la ecuación de grosor apropiado de tubería 2.1. Para tubería
soldada, cuando el ramal no intersecta la soldadura longitudinal del cabezal, el esfuerzo permisible básico S para la
tubería puede ser usado en la determinación de para el propósito solo de reforzar el calculo. Cuando el ramal si
hace la intersección de la soldadura longitudinal del ramal, los esfuerzos permisibles S del cabezal debiera ser
usado en el calculo. El esfuerzo permisible S del ramal debiera ser usado en el calculo de .
β = el Angulo mas pequeño entre los ejes del ramal y el cabezal.
30
(b)
Área de refuerzo requerida.
El área de refuerzo requerida
=
( 2 - sen β)
(2.10)
, es la mitad del area calculada por la ecuación 2.10, usando
Para una conexión de ramal bajo presión externa, el área
como el grosor requerido para presión externa.
=
(c)
para una conexión de ramal bajo presión interna es:
(2.11)
Área obtenible. El área obtenible para refuerzo esta definida como:
+ +
≥
.
Todas esas aéreas están dentro de la zona de refuerzo y son definidas mas ampliamente a continuación.
1.
El área es el área resultante del exceso de grosor en la pared del tubo cabezal:
=(2
2.
El área
-
)(
-
-c )
(2.12)
es el área resultante del exceso de grosor en la pared del tubo ramal:
=
(2.13)
Si el esfuerzo permisible para la pared del tubo del ramal es menor que la calculada para el cabezal, su área
calculada debe ser reducida en proporción a los valores de esfuerzos permisibles del ramal al cabezal en la
determinación de sus
contribuciones al área .
3.
es el área de otros materiales suministrados por la soldadura y refuerzos apropiados adicionales ver
El área
inciso (f) las áreas de soldadura debieran estar basadas en las dimensiones mínimas especificadas en las figuras
de conexiones típicas soldadas de ramal y detalles aceptables para uniones soldadas mostrados en la pagina
29, excepto que mayores dimensiones puedan ser usadas si el soldador ha sido instruido específicamente para
hacer las soldaduras de estas dimensiones.
(d)
Zona de refuerzo
La zona de refuerzo es un paralelogramo cuya longitud se extiende una distancia sobre cada
uno de los lados del centro de línea del tubo ramal y cuyo ancho comienza en la superficie interior de la tubería del cabezal
( en su posición corroída ) y se extiende mas alla de la superficie exterior del cabezal a una distancia perpendicular .
(e)
Ramales múltiples
Cuando dos o mas conexiones de ramal están espaciadas tan cerradamente que sus zonas de
refuerzo se traslapan, las distancias entre centros de las aperturas debiera ser al menos 1 ½ veces su diámetro promedio, y
31
(f)
el área de refuerzo entre cualquiera de dos aperturas debiera ser no menor que el 50% del total que ambas requieran. Cada
una de las aperturas deberá tener adecuado refuerzo de acuerdo a los incisos (b) y (c). Ninguna parte de la sección
transversal de metal se puede aplicar a mas de una apertura, o ser evaluada mas de una vez en cualquier área combinada
( consultar Estándar ES-7 del instituto de fabricación de tubería PFI para recomendaciones detalladas sobre el espaciado
entre boquillas soldables ).
Refuerzos adicionales.
1.- Refuerzo adicionado en la forma de un anillo o silleta como parte del área deberá ser de un ancho razonablemente
constante.
2.- El material usado para el refuerzo puede diferir del que forma parte del cabezal si es compatible con el material del
ramal y el cabezal, con respecto a la soldabilidad, requerimientos de tratamiento térmico, corrosión galvánica, expansión
térmica, etc.
3.- Si el esfuerzo permisible para el material de refuerzo es menor que el del material del cabezal, su área calculada debe
ser reducida en la proporción de los valores de esfuerzo permisible en la determinación de su contribución al área .
4.- Ningún crédito adicional puede ser otorgado para un material teniendo valores de esfuerzo mayores que el del tubo
cabezal.
Ejemplo
Un tubo de 10”Ø tiene 650°F y 400 psig como condiciones de diseño; esta hecho de A.C. sin costura ASTM A53 grado B ced 20. La
corrosión permisible es o.03 pulg. Tiene un ramal de 4”Ø del mismo material. ¿ cuales serán las dimensiones apropiadas para el
refuerzo, si esta hecho de un material de placa de igual calidad que la del material de tubería?.
Partiremos por el cálculo del grosor mínimo requerido para ambos tubos cabezal 10”Ø y ramal 4”Ø desde la ecuación básica:
=
(2.14)
Esfuerzo permisible para ASTM A53 gado B a 650°F = 15 000 psi/
De la tabla 2.1, el factor Y = 0.4 ( debajo de 900°F )
.
Para el cabezal,
=
Para el ramal,
=
Entonces:
El grosor mínimo de tubo 10” ced 20 = 0.219 pulg
Exceso = 0.219 - 0.418 -0.03 = 0.0472 pulg
El grosor mínimo de tubo 4” ced 40 = 0.207 pulg.
.
.
.
.
.
= 0.1418 pulg
= 0.0593 pulg
32
Exceso = 0.207 - 0.0593 - 0.03 = 0.1177 pulg.
Los grosores mínimos de arriba son las dimensiones de cedula nominales menos 12.5% de tolerancia de molino (MT) permitidos por
los estándares.
Longitud efectiva, = 4.5 - 2( 0.1177) =4.2646 pulg
= = 4.2646 pulg
La es el mínimo de 2.5( - c ) ó 2.5 ( - c ) + , esto es , el minimo de 2.5 x 0.22 ó 2.5 x0.207 +0.25 (se asume ¼” de
refuerzo).
Es claro, que la primera condición gobierna, de manera tal que = 0.55 pulg.
El área requerida =
x
= 0.1418 x 4.2646 = 0.6047
El área de compensación obtenible para el cabezal,
=(2
El área de compensación obtenible para el ramal,
=2
-
)(
(
)= 1.1 x 0.1117 = 0.1294
Compensación total obtenible sin atenuador reforsante = 0.3306
Área de sección transversal de atenuador requerida =
)= 4.2646 x 0.0472 = 0.2012
.
.
.
.
Este resulta en un anillo con 11.75 pulg de diámetro exterior,
.
= 0.1370
.
" de ancho, ¼” grueso. Nuestra negación de que el área del cordón
de soldadura no hace diferencia en la práctica; debe ser señalado, sin embargo, que para un servicio de esta severidad un weldolet
debería ser preferido. Para mas ejemplos de problemas, ver en el apéndice la tabla A5.
Ejercicios
1.
2.
3.
Calcular el grosor de diseño para presión interna para un tubo de 8”Ø Acero al carbón ASTM A106 grado B bajo 420 psig a
800°F. Si la tolerancia de molino (MT) = 12.5% y la corrosión permisible es 0.05 pulg. Seleccionar el gorsor comercial
asequible.
Calcular la máxima presión permisible la cual pueda ser soportable en un tubo de 12”Ø de peso estándar ASTM A53 grado B
a 725°F. Asumir una MT usual y o.1 “ para corrosión permisible.
Seleccionar el grosor comercialmente asequible para soportar 500 psig a 700°F en tubería de 12”Ø en material tipo A106
grado A, MT es 12.5% , y su corrosión permisble es 0.06 pulg.
Referencia
1.
Roarque, R.J.
“ Formules for Stress and strain “
33
CAPITULO TRES
Calculo del claro de tuberías
El claro máximo permisible para sistemas de tuberías horizontales, esta limitado por tres factores principales: esfuerzos de flexion,
deflexión vertical, y frecuencia natural. Para la frecuencia natural relativa y limitación de deflexión, el claro permisible puede ser
determinado como el meno r de los espacios de soporte calculados basados sobre el esfuerzo y la deflexión.
3.1
Limitaciones de claro
La formulación y ecuación obtenida depende sobre las condiciones asumidas en los extremos. Si se asume unbrazo de tubería,
simplemente soportado en ambos extremos; se obtienen las ecuaciones 3.1 y 3.2 ( referencia 1 ): estas condiciones de extremos nos
da mas altos esfuerzos y pandeos y por lo tanto resulta en un claro conservador.
L=
.
L=
∆
.
basado sobre limitación de esfuerzos
(3.1)
basado sobre limitación de deflexión
(3.2)
Las condiciones en los extremos pueden también ser asumidas como una media entre una viga uniformemente cargada simplemente
soportada en ambos extremos y una viga uniformemente cargada con ambos extremos fijos. Con esta condición ( referencia 2 ) se
obtienen las ecuaciones 3.3 y 3.4:
L=
.
L=
∆
.
basado sobre limitación de esfuerzos
(3.3)
basado sobre limitación de deflexión
(3.4)
Donde : L = Claro de tubería permisible, pies.
Z = Modulo de sección del tubo,
.
34
= Esfuerzo permisible a la tensión para el material de tubería a la temperatura de diseño, psi (conocida como esfuerzo
permisible caliente)
W = Peso total de tubo, libras/pie = peso metal + peso contenido + peso aislamiento.
∆ = Deflexión permisible o pandeo. Pulg.
I = Momento de área o de inercia del tubo,
.
E = Modulo de elasticidad del material de la tubería a la temperatura de diseño, psi (conocido como modulo de
elasticidad ).
Las excepciones son:
1.
La tubería esta en un estado estático, excepto por el movimiento inducido por los cambios de temperatura. Los
efectos de pulsación, vibración, ladeo, o terremoto no son tomados en cuenta.
2.
Cargas concentradas similares a válvulas no son consideradas en las ecuaciones 3.1 a 3.4.
3.2
Frecuencia natural
Para la mayoría de tuberías de refinería una frecuencia natural de cerca de 4 cps (ciclos por segundo) es suficiente para evitar
resonancia en líneas de tubería no pulsantes. Sin embargo, la frecuencia natural en cps esta relacionada a la máxima deflexión ∆
en pulgadas por:
=
Donde: g = aceleración debido a la gravedad, 386 pulg/
∆
=
.
√∆
( 32.12 pies/
(3.5)
).
Por lo tanto la frecuencia natural para una viga simple correspondiente a 1.00 pulg de pandeo es 3.12 cps. Una de las razones para
limitar la deflexión es hacer la tubería lo bastante rígida con una frecuencia natural lo bastante alta para evitar amplitudes grandes
bajo cualquier pequeña fuerza perturbante. Aunque esta puede parecer bastante baja, en la practica la frecuencia natural será mas
alta a causa de (1) momentos en los extremos, negados aquí , que elevarán la frecuencia por mas de 15%; (2) el claro critico es
usualmente limitado por los esfuerzos y es raramente alcanzado; y (3) el peso asumido del tubo es frecuentemente mas grande que la
carga real.
Para la relación frecuencia natural y limitaciones de deflexión, el claro máximo es así determinado por los valores mas pequeños
obtenidos de las ecuaciones 3.3 y 3.4.
El claro calculado es entonces multiplicado por el factor de reducción de claro. La figura 3.1 muestra diferentes arreglos de tubería y
el factor de reducción de claro f’ ( referencia 3 ); como se puede ver, el factor de reducción de claro es menor a 1.0.
Asumiendo que la tubería esta simplemente soportada en ambos extremos y que la válvula esta colocada en la mitad del claro ( caso 6
de la figura 3.1 , a = b = L/2 ), las ecuaciones 3.6 y 3.7 pueden ser derivadas:
35
Esfuerzos de flexión =
Deflexion =
Donde
.
(3.6)
.
(3.7)
= carga concentrada similar a la válvula en libras.
Figura 3.1 Casos del 1 al 6 de factores de reducción de claro de tuberías.
Se puede ver fácilmente que las ecuaciones 3.6 y 3.7 pueden ser usadas para calcular esfuerzos de flexión reales y deflexiones cuando
el claro es conocido o asumido.
Se pueden usar factores de reducción de claro para calcular claros permisibles para tubería con pesos concentrados similares a
válvulas donde sea a lo largo de su claro ( caso 6 fig 3.1 ) . Para una viga con extremos fijos el factor de reducción de claro se obtiene
( referencia 4 ) por la comparación del momento actuando en el soporte con el momento obtenido de solo el peso uniformemente
distribuido y esta dado por:
f’ =
Donde:
a =
,
(3.8)
β =
La tabla 3.1 nos da valores de f’ para diferentes valores de a y β .
36
Tabla 3.1
Factor de reducción de claro f’ para localización de válvula (usando ecuación 3.8)
3.3
Drenaje
Es frecuentemente necesario que los sistemas de tuberías que se van a instalar se puedan drenar por gravedad, preferentemente en
dirección del flujo normal; para alcanzar este drenaje cada uno de los claros debe ser espaciado de manera tal que la parte baja
quede abajo del máximo pandeo de la tubería. El espaciado de los claros de tubería es la relación éntrela caída en elevación y la
longitud del claro; esto es llamado pendiente promedio y se expresa en pulgadas por pie.
Revisión de la pendiente para drenaje.
Se debe hacer un análisis exhaustivo para propiciar una caída en elevación (pendiente) apropiada para el drenaje.
La condición para un buen drenaje es :
G≤
(3.10)
En el calculo del modulo de sección y el momento de inercia de la tubería, la corrosión permisible puede ser incluida, lo cual
resultará en un ligeramente mas alto claro.
La tabla 3.2 nos da los tipos de masa de materiales aislamiento de tuberías comunes. Los otros tipos son conocidos como reflectivos y
se usan en el interior de edificios de reactor en plantas nucleares ( referencia 7 ).
Tabla 3.2
Materiales de aislamiento de tubería común ( tipo de masa )
37
Para ilustrar el uso de las ecuaciones precedentes se realizaron los ejemplos de problemas siguientes.
Ejemplo 1
Calcular el claro permisible para un tubo de 10”Ø con pared estándar operando a 400°F; el material de tubería es acero al carbón
A106 grado B; el tubo esta lleno con aceite crudo cuya gravedad especifica es 1.2; tiene un ailamiento de 2” de grueso de silicato de
; el peso de metal, peso del contenido, y péso del aislamiento puede también ser obtenido
calcio con una densidad de 11 libras/
de cualquier tabla estándar. Se asume que la máxima deflexión permitida es 5/8”(.625 pulg).
Peso propio del tubo =
( densidad del acero)(longitud)= ( 10.75 - 10.02 ) (0.283) (12) = 40.44 lb/pie
Peso del contenido =
(largo) (densidad) =
10.02
(12)
.
= 34.17 lb/pie
(largo) (densidad) = ( 14.75 - 10.75 )(12)(
Peso del aislamiento =
) = 6.12 lb/pie
Peso total de la tubería = 40.44 + 34.17 + 6.12 lb/pie = 80.73 lb/pie
Usando la ecuación 3.3 basada en la limitación de esfuerzos:
Claro L =
.
Z = modulo de sección = 29.9
= esfuerzo permisible del material de tubería a la temperatura de diseño = 22 900 psi para acero al carbón A106
grado B a 400°F en el código B31.3 (apéndice tabla A1)
Claro L =
.
.
= 58.2 pies
.
Usando la ecuación 3.4 basada sobre la limitación de deflexión permisible de 5/8”:
Claro L =
∆
donde:
.
E = modulo de Young(psi) a 400°F para acero al carbón con contenido de o.3 % o menos= 27 x10 psi
I = area del momento de inercia del tubo = 160.7
=
.
.
.
= 39.7 pies
Seleccionando entre el mas pequeño de los claros ( 58.2 pies ó 39.7 pies ) entonces el claro es 39.7 pies.
Ejemplo 2
Calcular también el claro máximo permisible en los siguientes casos ( usando la información básica del ejemplo 1).
(a) Si una deflexión de 1” es permitida.
38
(b) Si el material del tubo fuera acero inoxidable A312 TP 304.
(c) Si el material del tubo fuera aluminio sin costura B241 grado 6061 T6.
(d) Si el tubo fuera de bronce rojo, sin costura B43 ( bronce comercial 66Cu - 343n).
(e) Si se usa tubo de níquel ( NiCu, especificación B 165,P No 42, grado 400,anillado en caliente ).
Caso (a):
Si se permite una pulgada de deflexión estática:
.
L=
Caso (b)
.
.
= 44.6 pies
Si el material del tubo fuera acero inoxidable A312 TP 304.( tubo 18 Cr - 8 Ni ):
L=
.
L=
∆
.
.
= 52.6 pies
.
/
.
.
.
.
.
= 39.56 pies
El claro requerido, L = 39.56
Caso (c)
Si el material del tubo fuera aluminio sin costura B241 grado 6061 T6 a 400°F:
L=
.
L=
∆
.
.
= 28.8 pies
.
/
.
.
.
.
= 30.0 pies
.
El claro requerido, L = 28.8 pies
Caso (d)
Si el tubo fuera de bronce rojo, sin costura B43 ( bronce comercial 66Cu - 343n).
L=
.
L=
∆
.
.
= 44.2 pies
.
/
.
.
.
.
.
= 37.1 pies
El claro requerido, L = 37.1 pies
39
Tablas de claro: Para proporcionar al lector con una referencia rápida de valores de claro; se presentan las tablas 3.3a y 3.3b .
Tabla 3.3a
Claros máximos para líneas de tuberías horizontales ( pies )
( Seleccionar la mas pequeña de L y L’ )
40
Tabla 3.3b
Factores de calculo (
,
y
) para claros.
Las tablas se basaron en las siguientes condiciones:
1. El material de tubería es acero al carbón A53 grado A; la tabla 3.3a se aplica conservadoramente a todos lo otros aceros.
2. Los rangos de temperatura de cero a 650°F. A 650°F, = 12 000 psi
El modulo de elasticidad = 25.2 x 10 del código de tubería.
3. La gravedad especifica del fluido es 1.0 ( agua ).
4. La densidad del aislamiento es 11 lb/
El grosor del aislamiento es 1½” para tubos de 1 - 4 “Ø.
2” para tubos de 6 - 14 “Ø.
2½” para tubos de 16 - 24 “Ø.
5. La tubería fue tratada como una viga horizontal, soportada en ambos extremos, conduciendo una carga uniforme igual al
peso combinado del metal, agua y aislamiento.
6. La máxima deflexión estática fue de 1 pulgada y la frecuencia natural fue 3.12 cps.
7. El esfuerzo de flexión máximo fue igualado a los esfuerzos máximos permisibles igual a la mitad del esfuerzo caliente ..??
Para otros valores de esfuerzos permisibles, deflexión, y frecuencia natural; los valores de claro dados en la tabla 3.3a necesitan ser
multiplicados por los factores de calculo de claro (dados en la tabla 3.3b) , y .
Los valores en la tabla 3.3b se alcanzaron como sigue:
½
1. Para cualquier otro esfuerzo permisible , el claro máximo es L, donde =
.
2. Para deflexiones diferentes a 1”, el claro máximo de tubería es
3. Para frecuencia natural f diferente a 3.12 cps , el claro máximo es
L’ donde
L´, donde
=
∆ .
=
.
.
Estos factores de calculo están dados en la tabla 3.3b para algunos valores de y f . Estos factores de calculo no debieran ser
confundidos con los factores de reducción de claro dados anteriormente en la figura 3.1.
41
Ejemplo
1. Usando la tabla 3.3 a , calcular el máximo claro permitido para un tubo 14”Ø. ( asumir = 12 000 psi, ∆=1” , y f =3.12 cps)
Claro L considerando los esfuerzos de la tabla 3.3 a = 43 pies
Claro L’ considerando la deflexión = 44 pies
Se selecciona el mas pequeño de los dos claros , el cual es 43 pies.
2. Calcular el claro si fuera 10 000 psi.
De la tabla 3.3 b , el factor de calculo es =0.913, claro = 0.913 (43) = 39.2 pies
3. Calcular el claro si ∆ = ½”
De la tabla 3.3 b , factor de calculo es =0.841, claro = 0.841 (44) = 37 pies
4. Calcular el claro si el tubo esta conectado a un compresor con velocidad de 8 cps.
De la tabla 3.3 b el factor de calculo es =0.625, claro = 0.625 (44) = 27.5 pies
El cálculo del claro permisible bajo cargas dinámicas es complicado. La formula conservadora para el calculo del espacio de fijación
( referencia 5) basada en el criterio de esfuerzo esta dada por :
L ≤ 2.19
(3.11)
Donde K = coeficiente sísmico dependiendo del espectro de respuesta del piso (múltiplos de la aceleración).
El criterio de deflexión dinámica ( referencia 4 ) puede ser usado para calcular el claro permisible bajo carga dinámica.
Para un claro de viga simple simplemente soportado, la deflexión máxima para tomarse como modulo esta dada por:
Máxima ∆ =
(3.12)
Donde m = tubo masa/pie
E = modulo de elasticidad, psi
I = momento de inercia,
= aceleración sísmica del tubo, pies/
3.4
Espaciado de guías para carga de viento
La tabla 3.4 da el espaciado máximo de guías para tubería vertical.
Tabla 3.4
Espaciado máximo de guías
Tamaño nominal de tuberías (pulg)
1
1½
2
3
Espaciado de guías (pies)
22
23
24
27
4
29
42
Tamaño nominal de tuberías (pulg)
6
8
10
12
14
16
18
20
24
Espaciado de guías (pies)
33
37
41
45
47
50
53
56
60
Notas:
1. Las guías debieran mantenerse a cerca de 40 diámetros de tubería claros de las esquinas ó
espiras.
2. El uso de guías de tubería sobre líneas calientes debe ser investigado para asegurar que
ninguna fuerza mayor o esfuerzo sea trasmitido por el sistema de tubería debido a la localización
de la guía.
3. El calculo de cargas de viento sobre tuberías esta dado en la referencia 6.
Tabla 3.5
Espaciado sugerido de soportes de tubería
Notas:
1.
Espaciado máximo sugerido entre soportes de tubería para tuberías estándar o mas pesadas que corren rectas a una
temperatura máxima de operación de 750°F.
2.
No se aplica donde los cálculos de claro se hicieron o donde hay cargas concentradas entre los soporte como bridas,
válvulas, y especialidades.
3.
El espaciado esta basado sobre un máximo de esfuerzos de flexión y cortantes de 1500 psi y tubería aislada llena de agua o
el peso equivalente de tubería de acero para gas, vapor, o servicios de aire y el espaciado de la línea es tal que un pandeo de
0.1 pulgadas entre soportes es permisible.
43
3.5
Reglas de diseño para soportes de tubería.
Espaciado de soportes de tubería.
Los soportes para tubería con eje longitudinal en aproximadamente una posición horizontal, deberían ser espaciados para prevenir
esfuerzos de corte excesivos resultantes del pandeo o flexión en la tubería, dando especial consideración cuando componentes tales
como bombas y válvulas imponen cargas concentradas. Los claros máximos sugeridos para espaciado de soportes de peso, para
tuberías de peso estándar o más pesadas están dadas en la tabla 3.5.
Ejercicios
1.
2.
3.
4.
5.
1.
2.
3.
4.
5.
6.
7.
Calcular el máximo claro permisible para un tubo de 16”Ø de peso estándar. El aislamiento es de silicato de calcio delgado
. El material de la tubería es acero al carbón A 106 grado B y la temperatura del aceite es
con densidad de 12.25 lb/
600°F. Asumir que la deflexión máxima permisible es 1 pulgada.
Calcular el claro, si fue localizada una válvula con un peso de 1050 libras a la mitad de la distancia del claro de un soporte
del ejercicio 1.
Calcular el claro, si fue localizada una válvula con un peso de 1050 libras a un tercio de la distancia del claro de un soporte
del ejercicio 1.
Calcular el claro, si la tubería considerada en el ejercicio 1 tiene un codo a 90° entre los soportes.
Calcula la deflexión estatica en un tubo de 10”Ø ced 80 acero inoxidable lleno de agua y con 3” de aislamiento de fibra de
vidrio.
Referencias
Barc,W et al, Pipe supports for industrial Piping Systems. Procon Inc. 1963
Fluor Design Guides and Q. Truong. Seminar of piping systems. A&M University. Texas.
DMI,Inc. Design Standars.
Niyogi, B.K. “ Simplied Seismic Analysis Methods for small Pipes” ASME 78-PVP-4.3
Stevenson et al. “Seismic Design of Small Diameter Pipe and Tubing For Nuclear Power Plants” Paper #314,
Fifth World Conference of Earthquake Engineering. Rome, 1973.
ANSI Standard A 58.1 “ Wind loads for Buildings and other Structures”.
Wilkes, Gordon B. “ Heat Insulation” Wiley, N.Y.
44
CAPITULO cuatro
Códigos de tubería ANSI y
Códigos de tubería ASME
Los códigos de tubería ANSI y los códigos de recipientes a Presión ASME nos dan guías para el diseño de tuberías. En general, la
ultima revisión debiera ser usada. En el diseño de tubería para una planta de potencia nuclear, el código de registro, el cuan no
necesaria la ultima revisión, para una planta especifica puede ser usado.
Los códigos relacionados al diseño de tubería incluyen:
1. ANSI B31.1, Tubería de Potencia (referencia 1)
2. ANSI B31.3, Tubería para plantas químicas y refinerías de petróleo (referencia 2)
3. ANSI B31.4, Tubería para transporte de líquidos (referencia 3).
4. ANSI B31.8, Tubería para transporte de gas (referencia 4)
5. ASME Sección III, Diseño de componentes nucleares (referencia 5)(el diseño de estos esta en el capitulo 10)
Subseccion NA Apéndice general. Propiedades de materiales.
Subseccion NB Tuberías clase 1 (tuberías de alta energía)
Subseccion NC
Tuberías clase 2
Subseccion ND Tuberías clase 3
Subseccion NF
Diseño de soportes.
4.1
Presión Interna y esfuerzos longitudinales
Los esfuerzos permisibles de código están diseñados para prevenir falla de los sistemas de tubería; los dos tipos de falla contra que
las tuberías debieran ser protegidas son:
1.
Sobreesfuerzos directos o falla debido a la presión, peso, viento, terremoto y otras cargas primarias.
2.
Fatiga o distorsión debido a tirones de desplazamiento (generalmente efectos térmicos) los cuales son cargas
secundarias.
Los limites de los esfuerzos calculados causados por cargas sostenidas y tirones de desplazamiento son:
45
1.
Esfuerzos de presión interna:
Los esfuerzos debidos a la presión interna son considerados seguros cuando el
grosor de la pared del tubo y cualquier refuerzo son adecuados (ver cálculos de grosor en el capitulo 2).
2.
Esfuerzos longitudinales ( ): La suma de los esfuerzos longitudinales resultantes de la presión, peso, y otras
cargas sostenidas no excederá los esfuerzos básicos permisibles para el material a la temperatura máxima del
metal . El grosor usado de tubo usado en el calculo de debe ser reducido por tolerancias tales como
corrosión, erosión, tolerancia de manufactura y profundidad de ranura.
3.
Rango de esfuerzos permisibles para esfuerzos de desplazamiento:
dado por:
= f (1.25
Donde
+ 0.25
)
El rango de esfuerzos permisibles
esta
(4.1)
= Esfuerzos permisibles básicos para el material a la temperatura mínima (fría) ,psi.
= esfuerzo caliente, psi.
f = Factor de reducción de esfuerzo para condiciones cíclicas para el numero total de los ciclos de temperatura
completos sobre la vida esperada.
La tabla 4.1 nos da factores de reducción, f, en el rango de valores de esfuerzo.
Tabla 4.1 Factores de reducción para el rango de esfuerzos
Numero de ciclos
Factor f
7 000 y menor
1.0
7 000 a 14 000
0.9
14 000 a 22 000
0.8
22 000 a 45 000
0.7
45 000 a 100 000
0.6
Arriba de 100 000
0.5
Cuando
es mayor que el valor calculado de , la diferencia entre ellos puede ser sumada al termino 0.25
4.1. En este caso el rango de esfuerzo permisible llega a ser :
en la ecuación
46
-
= f [1.25
Tabla 4.2
Comparación de esfuerzos permisibles y de cedencia para tubería
Temperatura del metal °F
-20 a
Código
(4.2)
]
-100
200
300
400
500
600
650
700
750
800
850
900
950
1000
B31.3
20
20
20
20
18.9
17.3
17.0
16.8
13.0
10.8
-
-
-
-
B31.1
14.4
14.4
14.4
14.4
14.4
14.4
14.4
14.4
13
10.8
-
-
-
-
Secc III Clase 2
15
15
15
15
15
15
15
14.3
-
-
-
-
-
-
35
B31.3
20
18.1
17.4
17.2
17.1
16.8
16.6
16.3
13.2
12.8
12.1
10.9
8.0
5.8
30
B31.1
15
15
15
15
14.5
14
13.7
13.4
13.1
12.8
12
10.4
7.6
5.6
Secc III Clase 2
15
15
14.5
14.4
14.4
14.2
13.9
13.7
-
-
-
-
-
-
30
PNo.8
B31.3
20
20
20
18.7
17.5
16.4
16.2
16
15.6
15.2
14.9
14.6
14.4
13.8
30
18Cr - 8Ni
B31.1
18.8
15.7
14.1
13
12.2
11.4
11.2
11.1
10.8
10.6
10.4
10.2
10
9.8
Secc III Clase 2
17.5
16.6
16.1
15.5
15
14.5
14.3
14.1
-
-
-
-
-
-
A106 Grado B
30
A335 grado P5
5% Cr- ½Mo
A312 TP304
40
Se dan valores representativos de y en la tabla 4.2 para acero al carbón A335 5Cr-½Mo, y para acero inoxidable A312 TP 304
(referencia 1), B31.3 (referencia 2), y sección III (clase 2 subseccion NC, referencia 5). Como se puede ver el código B31.3 nos da
esfuerzos permisibles mayores, mientras que en la sección III materiales clase 2 se permiten mayores esfuerzos de cedencia. El
apéndice en la tabla A3 nos da valores B31.3 para la mayoría de materiales comunes. Para otros códigos, debieran usarse referencias
apropiadas en el diseño actual.
Se encuentran frecuentemente cálculos del rango de esfuerzos permisibles
mostrar el calculo de .
usando la ecuación 4.1. Se dan tres ejemplos para
Ejemplos
1.
Una tubería esta fabricada de acero al carbón sin costura ASTM A106 grado B; la temperatura de diseño es 700°F.
¿ Cual es el rango de esfuerzo de expansión permisible ?. Refiérase al ANSI B31.3 (ultima edición) para hallar los
a la temperatura mínima 100°F (por ejemplo, =20 000 lb/
) , el esfuerzo a 700°F
esfuerzos y
) Apéndice A3. En la ausencia de cualquier razón para tomar un valor
(por ejemplo, = 18 800 lb/
.
asumido menor f = 1.0; entonces = 1.0(1.25 x 20 000 +0.25 x 16 800 ) = 29 000 lb/
2.
Una tubería suministra vapor a un recipiente de proceso enchaquetado que esta operado en un proceso a lotes con
un ciclo de 4 horas; la temperatura del vapor es 200°F, y el material de la tubería es acero de baja y media
aleación sin costura, ASTM A335 5Cr-½Mo. Si la instalación es operada continuamente y la vida de diseño es de 12
años, ¿ Cual es el rango de esfuerzos permisibles para esfuerzos térmicos en la tubería ?
47
Esfuerzo permisible (frio) = = 20 000 lb/
Esfuerzo permisible (325°F) = =18 100 lb/
Numero de ciclos =
( Apéndice tabla A3 )
x 365 x 12 =26 280
F = 0.7 ( para 22 000 - 45 000 ciclos ) ( ver tabla 4.1 )
= f ( 1.25 +0.25 = 0.7(1.25 x 20 000 + 0.25 x 18 000) = 20 667 lb/
3.
Una línea en un sistema de alivio alcanza una temperatura de - 90°F cuando la válvula de alivio se levanta; el
material es acero inoxidable A312 TP 304 ( 18CR - 18 Ni ). ¿ Cual es el rango de esfuerzo de expansión permisible?
Tomar en cuenta dos anotaciones:
1.
2.
A causa de que las líneas de alivio no operan frecuentemente, nosotros estaremos justificados en asumir
que la tubería experimentará menos que 7 000 ciclos de esfuerzos; por lo tanto f = 1.0
El hecho de que el rango de la temperatura ambiente a la temperatura de operación es negativo no hace
diferencia; es el cambio de temperatura el asunto.
Para tubería sin costura ASTM A312 TP 304 , el esfuerzo permisible es ( minimo a 100°F )
= = 20 000
= f ( 1.25 +0.25
4.2
= 1.0(1.25 x 20 000 + 0.25 x 20 000) = 30 000 psi.
Requerimientos del código de tuberías para refinarías de petróleo para Análisis formal.
Del código ASME/ANSI b31.3- 2004 , subseccion 319.4.1.
Ningún análisis formal es requerido de flexibilidad adecuada para un sistema de tubería que:
(a) es un duplicado, o remplaza sin cambio significante, a un sistema operando con un registro de servicio
afortunado.
(b) pueda fácilmente ser juzgada adecuada por comparación con un sistema previamente analizado.
(c) es de un tamaño uniforme, no tiene mas de dos puntos de fijación, no hay sujeciones intermedias, y cae dentro
de los empíricos de la ecuación 4.3.
≤
(4.3)
Donde: D = Diámetro exterior de tubería, pulg (mm)
= Referencia del modulo de elasticidad a 70°F (21°C), psi (MPa), condición fría.
= 30 /
/
= 208 000 /
/
L = Longitud de tubería desarrollada entre anclajes, pies (m)
= Rango de esfuerzos de desplazamiento permisibles de la ecuación 4.1, ksi(MPa)
U = Distancia entre anclaje, en línea recta entre anclajes, pies(m)
48
y = Resultante de los tirones de desplazamiento totales, pulg(mm), a ser absorbidas por el sistema de tuberías.
A causa de que ninguna prueba general puede ser ofrecida de que la ecuación 4.3 será conservadora, se debiera ejercer
precaución al ejercerla en la aplicación de configuraciones anormales ( no parecidas a piernas con curvas “U”), para
tuberías de pared delgada y diámetro grande ( factores de intensificación de esfuerzos de 5 ó mas ), o para condiciones
donde movimientos extraños, otros en que la dirección conectando los puntos de anclaje constituyan una gran proporción
del trabajo de expansión.
El usuario debe estar enterado de que el cumplimiento con la ecuación 4.3 no nos asegura que las reacciones terminales
serán satisfactorias; un valor de 0.03 puede asumirse para la ecuación 4.3 , si no fue asequible suficiente información ( la
ecuación 4.3 no incluye el efecto del peso ).
Ejemplo 4
Checar si es necesario el análisis formal en el arreglo de tuberías dado en la figura 4.1; usando le ecuación 4.3
El diámetro es 10”Ø, la temperatura 300°F, el coeficiente es 0.023 pulg/pie para tubería de acero al carbón A106
grado B ( ver apéndice tabla A1 )
Figura 4.1
Arreglo tuberías.
La expansión en cada dirección y el movimiento terminal es :
∆ x = 40 (0.023) = 0.92 pulg
∆ y = (50 -10)(0.023)+(2 -1 ) = 1.92 pulg
∆ z = 15 (0.023) = 0.345 pulg
y = 0.92
1.92
0.119 = 2.13
D = Diámetro nominal = 10 pulg
= Modulo frio para acero al carbón = 27.9 x 10 psi ( apéndice tabla A2 )
L = longitud desarrollada = 15 + 10 + 15 +50 + 25 = 115 pies
U = distancia entre anclaje = 58.5 pies ( distancia en línea recta entre anclajes )
= f ( 1.25 +0.25 = 1.25( 20 000 + 0.25 x 20 000) = 30 000 psi.
49
La ecuación 4.3 estipula que el análisis formal es necesario si:
≤ 30
=
.
.
.
≤
(4.3)
= 0.00668
30
=
.
106
= 0.0322
A causa de que en los resultados 0.00668 ≤ 0.0322, ningún análisis formal es necesario desde el punto de vista de
flexibilidad térmica.
4.3
Momentos de flexión en plano y fuera de plano
El código B31.3 define momentos flexores en plano y fuera de plano los cuales son mostrados en las figuras 4.2 y 4.3.
Después de la aplicación del momento flexor , el codo o conexión ramal aun permanece en el plano original; pero
fue aplicado, el codo o conexión ramal van fuera del plano original. El
cuando el momento flexor fuera de plano
momento torsional cerca de los ejes de la tubería esta anotado por , el código B31.1( tubería de potencia) y el código
nuclear (ASME sección III) no diferencian entre momentos flexores en plano y fuera de plano. Ver tabla 10.1 para ecuaciones
de código nuclear.
Figura 4.2
Momentos en codos.
50
Figura 4.3 Momentos en plano y fuera de plano para conexiones ramal.
4.4
Factores de intensificación de esfuerzos.
Accesorios auxiliares de tubería como curvas ( por ejemplo, codos, codos fragmentados) y conexiones ramal ( por ejemplo,
te soldable, tes fabricadas ) tienen características de flexibilidad h, factor de flexibilidad k, y factores de intensificación de
esfuerzo (SIF). En esta área la mayoría de códigos incluyendo el estándar británico BS3351 usan el trabajo hecho por Markl
(referencia 6).La tabla 4.3 (reproducido del apéndice D, ANSI B31.3-2004) nos da ecuaciones para el calculo de valores h,
k, SIF en plano , y SIF fuera de plano . Note que otros códigos no permiten el uso de valores menores para el SIF
( 0.75/
fuera de plano comparado con el valor alto de ( 0.9/
para SIF en plan
Notas que se aplican a las tablas 4.3ª y 4.3b.
(1)
Los datos de factor de intensificación de esfuerzo y de en flexibilidad en las tablas 4.3 son para usarse en la
ausencia de datos mas directamente aplicables. Su validez ha sido demostrado para D /Ť≤100.
(2)
El factor de flexibilidad, k , en la tabla se aplica para flexión en cualquier plano: Los factores de flexibilidad, k, y
los factores de intensificación de esfuerzos, i , no deberán ser menos que la unidad; los factores para torsión igual
a la unidad. Ambos factores se aplican sobre la longitud del arco efectivo ( mostradas con líneas de centro pesadas
en los bocetos ) para codos curveados y fragmentados, y para la intersección de puntos para tes.
(3)
Un solo factor de intensificación igual a
.
puede ser usado para ambos
y , si se desea.
51
Tabla 4.3a
Factores de flexibilidad k y de intensificación de esfuerzos i
52
Tabla 4.3b
Carta de SIF y factor de flexibilidad.
53
Continuación de notas para las tablas 4.3a y 4.3b
(4)
Los valores de k e i pueden ser leídos directamente de la carta A, introduciendo la característica h computada de las
formulas dadas arriba. La nomenclatura es como sigue:
= Diámetro exterior del ramal.
= Radio de curvatura de la te soldable o curva de tubería.
= En una te radio de curvatura de bifurcación en la porción contorneada externa de la salida, ver detalle en la
tabla 4.3.
= Radio medio de la tubería principal. ver detalle en la tabla 4.3.
s = Distancia en línea recta entre los cruces de los segmentos con el radio de curvatura. ver detalle en la
tabla 4.3.
Ť = Para codos y codos fragmentados, el grosor de pared nominal de los accesorios = para tes, el grosor de
pared nominal de la tubería enchufada.
= En una te, el grosor de pared de donde empieza el ramal. ver detalle en la tabla 4.3.
Ť = Grosor de pared del refuerzo o silleta. ver detalle en la tabla 4.3.
Θ = La mitad del ángulo entre los ejes de dos gajos adyacentes.
(5)
Cuando se fijan bridas a uno o ambos extremos, los valores de k é i en la tabla serán corregidos por los factores
los cuales pueden ser leídos directamente de la carta B, usando el h computado.
(6)
El diseñador esta avisado que los accesorios soldables fundidos pueden tener paredes considerablemente mas
gruesas que la tubería que esta usando.. Grandes errores pueden ser introducidos a no ser que el efecto de estos
grosores mas grandes sean considerados.
En codos y curvaturas de pared delgada y diámetros grandes, la presión puede afectar significativamente las
magnitudes de k é i; para corregir los valores de la tabla,
(7)
dividir k entre
1+6
dividir i entre
1 + 3.25
,
Ť
Ť
(8)
Por consistencia use psi y pulg para sistema ingles; y kPa y mm para sistema métrico.
Cuando Ť es > 1½Ť, use h = 4Ť / .
(9)
El diseñador debe estar satisfecho que esta fabricación tiene un rango de presión equivalente a tubo recto.
(10)
Los factores mostrados se aplican a flexión, el factor de flexibilidad para torsión es igual a 0.9.
54
≥ 1.5 Ť , una flexibilidad característica de 4.4 Ť / puede ser usada.
(11)
Si ≥
y
(12)
Los factores de intensificación de esfuerzo fuera de plano (SIF) para una conexión ramal reductora con una relación
de diámetro cabezal-ramal de 0.5 <
< 1.0 puede ser no conservadora. Una soldadura cóncava suave ha sido
mostrada para reducir el SIF. La selección de una SIF apropiada es responsabilidad del diseñador.
(13)
Los factores de intensificación de esfuerzos para conexiones ramal esta basada sobre pruebas con al menos dos
diámetros de de tubería de cabezal en cada lado del centro de línea del ramal. Ramales m as cerradamente
cargados pueden requerir consideración especial.
(14)
2.1 máximo o 2.1
Ť
, pero no menor que 1.3
es la longitu de soldadura de la pierna ( ver figura a
continuación). Para longitudes de pierna desiguales, use la mas pequeña pierna para
.
Dimensiones mínimas de soldadura para componentes enchufables de tubería diferentes a bridas.
Ejemplo 5
Calcular SIF y factor de flexibilidad para un codo de 12”Ø cedula estándar radio largo.
(a) Para un codo soldable,
Radio de curvatura = = 1.5(diámetro nominal) = 1.5(12) = 18 pulg
Ť = grosor de pared nominal = 0.375 pulg ( ver apéndice tabla A4, propiedades de tubería ) y asumir que el codo y la
tubería tienen el mismo grosor.
Ť
= radio medio del tubo =
h = Flexibilidad característica =
k = factor de flexibilidad =
.
=
Ť
=
.
.
= 6.1875 pulg
( ecuación de la tabla 4.3 a) =
.
.
.
.
= 0.176
= 9.358
55
= factor de intensificación de esfuerzos en plano=
.
= SIF fuera de plano =
El valor menor =
.
.
=
.
=
.
= 2.86
.
= 2.4
.
esta permitido para B31.3 B31.4; si se desea un valor mas alto i =
.
puede ser usado para
ambas y . Para B31.1 tuberías de potencia y tubería nuclear, sección III, clases de tubería 2 y 3 , se usa
solo el valor mas alto.
(b) Si uno de los extremos esta bridado, el factor de corrección =
SIF en plano =
SIF fuera de plano =
.
= 0.564(
.
.
.
=
= .176
= 5.25
= 0.564(2.86) = 1.6
= 0.5664 (2.4) = 1.345
Para modelado de bridas en los codos, los valores mas bajos de SIF pueden usarse ventajosamente; sin embargo, el factor de
flexibilidad también ha sido reducido lo cual no es deseable.
Codos fragmentados
Los codos fragmentados serán usados, cuando es mas económico, para cambios en dirección en tubería de agua de acero, líneas de
drenaje, y en tuberías internas en recipientes a presión, en el cual las limitaciones de espacio prohíben el uso de codos. Los codos
fragmentados en líneas de succión horizontal de bombas debieran estar a un mínimo de seis diámetros de tubería de la brida de
succion. Las ecuaciones para calcular los factores de intensificación de esfuerzo para los codos fragmentados están dados en la tabla
4.3 a. El codo fragmentado en sus gajos puede ser espaciado en una manera cerrada o en una manera abierta, tal y como esta
determinado por el uso de las siguientes ecuaciones:
El fragmentado esta espaciado cerradamente, si el espacio del fragmento S es:
S<
( 1 + tanθ )
(4.4 a)
= radio curvatura =
(4.4 b)
El fragmentado esta espaciado abiertamente, si el espacio del fragmento S es:
S≥
( 1 + tanθ )
(4.4 c)
(4.4 d)
56
Donde θ = ángulo del gajo(fragmento), grados.
= radio medio de la tubería empalmada, pulg.
( para cálculos de presión interna máxima permisible, ver ecuaciones 2.8 a, 2.8 b y 2.8 c )
El ángulo del gajo θ es igual a 11.25° para un codo fragmentado de 5 piezas (o cuatro soldaduras) en el boceto (d) en la tabla 4.4 ;
θ es igual a 15° para un codo de cuatro piezas (o tres soldaduras)en el boceto (c)en la tabla 4.4; y θ es igual a 22.5° para un codo
de tres piezas ( o dos soldaduras) en el boceto (b) en la tabla 4.4. Esta tabla muestra esos codos fragmentados (gajos) y también nos
da el espacio del gajo S.
Tabla 4.4
Dimensiones de espaciado de gajos parea un codo fragmentado, pulgadas.
57
Ejemplo 6.
Calcular el SIF y el factor de flexibilidad k para un codo fragmentado de 8ӯ de cuatro piezas; el grosor de la placa es 0.322
pulgadas.
Para una tubería de 8”Ø, =radio medio= 4.152 pulg. Para un codo fragmentado de 4 piezas (3 soldaduras), θ=
ángulo del gajo=15°
De la tabla 4.4 , S=espaciado del gajo=6 ”. Checar para gajos ampliamente y cerradamente espaciados: (1+tan 15)=5.26
Lo cual es menos que el espaciado de gajos de la tabla. Por esto el gajo dado ,es un gajo ampliamente espaciado.
Usando la ecuación del código, tabla 4.3 a.
Ť
h = flexibilidad característica=
.
k= factor de flexibilidad =
= = SIF =
.
=
2
.
=
4.152
= 0.1835
=6.24
.
.
=
.
.
.
= 2.78
La tabla 4.3 a nos da las ecuaciones para calcular los factores de flexibilidad y SIF para los siguientes tipos de intersección de ramal:
1.
Te soldable
2.
Te fabricada reforzada con cuello o silleta.
3.
Te fabricada sin refuerzo o injerto.
4.
Te soldable extruida.
5.
Inserto soldado en el contoeno ( weldolet )
6.
Ramal soldado sobre accesorio.
Las intersecciones de ramal son algunas veces identificados por nombres de marcas o nombres dados por manufactureros específicos.
Es importante recordar que el valor del SIF debiera no ser menos que 1 (nota 1 de la tabla 4.3 b)
Cuando el grosor del cuello de refuerzo T, es mas grande que 1.5 veces el grosor de la tubería Ť, la ecuación para calcular h se
convierte en
h=4
Ť
(ver nota 5, tabla 4.3 b)
(4.4 e)
Cuando esta condición es alcanzada h no es mas grande que la función del grosor del cuello de refuerzo, eso significa que no puede
darse crédito para una porción de grosor de cuello que es mayor que 1.5 veces el grosor de tubería.
Los valores de SIF para la mayoría de tipos de intersección de ramal son una función de las dimensiones del tubo cabezal y no del
ramal.
58
Ejemplo 7
Calcular SIF y factor k para un tubo de 8”Ø cedula estándar con un ramal de 4”Ø, si:
(a) si la intersección es una te fabricada no reforzada.
(b) si el grosor del cuello de refuerzo usado es igual al grosor del cabezal.
(c) si el grosor del cuello de refuerzo es 0.57 pulg
El grosor de pared del cabezal es Ť= 0.322 pulg; el radio medio de la tubería es
Ť
= radio medio del tubo =
=
.
.
= 4.1515 pulg
(a) La te fabricada no reforzada:
h = flexibilidad característica = Ť/ =0.322/4.152 = 0.0776
k = factor de flexibilidad = 1
=SIF fuera de plano = 0.9/
=SIF en plano =
= 0.9 / 0.776 = 4.95
= (4.95) + = 3.96
(b) La te fabricada reforzada:
Ť = grosor cuello refuerzo = 0.322 pulg, k = 1.0
h=
Ť ½Ť
Ť
=
.
½ .
.
.
=SIF fuera de plano = 0.9/
=SIF en plano =
=
.
.
.
= 0.213
= 0.9 / 0.213 = 2.52
= (2.52) + = 2.14
(c) El grosor del cuello de refuerzo = 0.57 pulg. Ver nota 5 de la tabla 4.3 b. Cuando Ť es > 1½Ť, use h = 4Ť / .
1.5(0.375) = 0.5625
Dado el grosor del cuello Ť = 0.57 pulg >1.5(0.375)
Por lo tanto ,
h = 4Ť /
=4
.
.
) = 0.3613
59
=SIF fuera de plano = 0.9/
=SIF en plano =
= 0.9 / 0.3613 = 1.18
= (1.18) + = 1.137
K = 1.0
4.5
Efecto de la presión sobre los factores de intensificación de esfuerzos y la flexibilidad.
Algunos códigos de tuberías ( referencias 2 y 3 ) dan formulas para corregir el factor de flexibilidad y el factor de intensificación de
esfuerzo (SIF) para codos o curvas. El efecto de la presión sobre el esfuerzo, fuerzas, y momentos por el uso de factores corregidos de
intensificación de esfuerzos y de flexibilidad se discuten a continuación.
Cuando el efecto de la presión es considerado, los valores de SIF son mas bajos, de este modo reducen el esfuerzo térmico real. Sin
embargo, la fuerza de anclaje se incrementa a causa de que flexibilidad en el codo se ha reducido. La presión puede afectar
significativamente la magnitud del factor de flexibilidad y el SIF en codos de pared delgada y diámetro grande.
Los factores de flexibilidad y SIF son constantes muy importante en cálculos de esfuerzo de tubería.
Tabla 4.5
Factores de flexibilidad e intensificación de esfuerzos para curvas.
La tabla 4.5 nos da ecuaciones para calcular flexibilidad característica h, factor de flexibilidad k , factores de
intensificación de esfuerzos en plano y fuera de plano ( y ) para codos y curvas.
El factor de flexibilidad k en la tabla se aplica para flexión en cualquier plano. El factor de flexibilidad k y el factor de intensificación
de esfuerzo i no debieran ser menos que la unidad; los factores para torsión igual a la unida. Ambos factores se aplican sobre la
longitud de arco efectiva ( mostrada por una línea de centros gruesa en el boceto anterior) para codos curveados.
Un factor de intensificación simple igual a 0.9 puede ser usada para ambos y si se desea.
El factor de corrección CFK para el factor de flexibilidad debido a la presión sobre codos y curvas esta dado por la ecuación 4.5 a:
CFK = 1 + 6
)
Ť
(4.5 a)
El factor de corrección CFI para SIF esta dado por la ecuación 4.5 b:
CFI = 1 + 3.25
)
Ť
(4.5 b)
60
Donde Ť = Grosor de pared nominal de los accesorios para codos o codos fragmentados, pulgadas.
= radio medio del tubo, PULG.
= Radio medio del codo soldable o curva de tubería, pulg.
P = Presión manométrica, psi.
= modulo frio de elasticidad, psi.
Las ecuaciones 4.5 a y b para factores de corrección están dados son dados por el (B31.3-2004) Tubería para plantas químicas y
refinerías de petróleo y transporte de líquidos de petróleo…..falta informacion
Falta informacion
….
Para ilustrar el efecto de la presión sobre el factor de flexibilidad y los factores de intensificación de esfuerzos, se muestra un
problema en la figura 4.4, usando codos soldables ( nodo 50 )
Figura 4.4
Espira de expansión simetrica
Ejemplo 8
El diámetro exterior de la tubería es 8.625 pulg.
Ť
= radio medio del tubo =
=
.
.
= 4.1515 pulg
Ť= 0.322 pulg
= 1.5(diámetro nominal) = 1.5(8) = 12 pulg
P = 250 psi
= 27.9 x 10 psi
La flexibilidad característica es:
h = Flexibilidad característica =
=SIF fuera de plano = 0.75/
Ť
( ecuación de la tabla 4.3 a) =
.
.
= 0.224
= 0.75 / 0.224 = 2.03
61
=SIF en plano = 0.9/
= 0.9 / 0.224 = 2.44
K = factor de flexibilidad =
.
.
=
.
= 7.366
El factor de corrección CFK para el factor de flexibilidad (ecuación 4.5 a)
CFK = 1 + 6
)
=1+6
Ť
.
El factor de flexibilidad corregido es:
.
.
106
)
.
.
= 1.02967
.
= 7.1537
El factor de corrección CFI para SIF ( ecuación 4.5 b )
CFI = 1 + 3.25
)
SIF en plano corregida =
.
Ť
.
106
)
.
.
.
= 1.03527
= 2.36
.
SIF fuera de plano corregida =
= 1 + 3.25
.
.
= 1.96
Note que el factor de flexibilidad y el factor de intensificación de esfuerzos se reduce cuando se considera el efecto de la presión
sobre codos. Para comparación de resultados se usaron cuatro diferentes diámetros con un rango de 6 a 12 pulgadas de diámetro
nominal.
Tabla 4.6
Efecto de la presión en codos ( nodo 50 ) ( presión = 250 psi )
62
La tabla 4.6 nos da los resultados obtenidos. Por ejemplo, con un diámetro exterior de tubería de 8.625 pulg, los factores SIF son
= 2.44 y = 2.03 cuando ningún efecto de presión fue considerado, resultando un esfuerzo de expansión de 18 396 psi en la
curva 50. Cuando el efecto de presión fue considerado, para la misma tubería de 8”Ø , se obtuvieron, = 2.36 y = 1.96, y el
esfuerzo de expansión de 18 009 psi en la curva 50 .
El porciento de cambio en los resultados debido al efecto de la presión para una línea de 8”Ø es:
Porciento de cambio ( mas bajo ) en el esfuerzo de expansión =
x 100 = 2.1 %
Porciento de cambio ( mas grande ) en la fuerza axial en el anclaje =
x 100 = 1.0 %
Como muestra la tabla 4.7 , los efectos de presión llegan a ser mas significativos en cuanto se incrementa la presión; para la misma
espira de expansión de tubo de 8.625 de diámetro exterior los rangos de presión fueron cambiados.
Tabla 4.7
Efecto de la presión en codos (nodo 50)
OD = 8.625 pulg, Grosor = 0.322 pulg, Temperatura = 450°F
Es posible que incluyendo el efecto de la presión sobre el SIF y sobre el factor de flexibilidad podía hacer la diferencia entre los
valores obtenidos del esfuerzo de expansión con y sin el efecto de presión. Este efecto puede ser significativo en el caso de codos de
pared delgada y diámetros grandes.
Como se ha estipulado antes solo los códigos de tuberías B31.3 yB31.4 han permitido el uso de la ecuación 4.5 b, para incluir el
efecto de la presión en el SIF. El trabajo básico sobre esta area y la formulación de las ecuaciones se halla en la referencia 7 y esta
información fue usada para reducir los esfuerzos en tuberías en el análisis de caso reales. Dos líneas de vapor de gran diámetro
(65.74pulg) y longitud (6 500 pies) fueron construidas para suministrar vapor saturado a 400°F a plantas de agua pesada en el
Ontario Hydro´s Bruce Nuclear Power Development ( referencia 8 ). En el análisis preliminar, se usaron las ecuaciones para
flexibilidad y factores de intensificación de esfuerzos dados en el código B31.1( referencia 1 ); en el análisis posterior las ecuaciones
4.5 a y b se usaron y la tubería fue calificada.
63
Esfuerzos en un sistema de tuberías
La ecuación para esfuerzos de expansión esta dada en la ecuación 4.6; la ecuación para los esfuerzos de flexión esta dada en la
ecuación 4.7. Para conexiones de ramal, la ecuación de esfuerzos de flexión resultantes requiere atención, a causa de que el valor del
modulo de sección Z, usado para cabezal y ramal es ligeramente diferente. ; las ecuaciones 4.8 y 4.9 muestran esta diferencia. El
valor calculado del esfuerzo de expansión
necesita ser mas bajo que el rango del esfuerzo de expansión , que se definió
anteriormente en la ecuación 4.1.
Los esfuerzos en un sistema de tuberías son generalmente bajos para variaciones de temperatura pequeñas, diámetros pequeños,
coeficientes de expansión pequeños, módulos bajos de elasticidad y la mas larga longitud de la tubería en dirección perpendicular a
la dirección de expansión.
El grosor de pared de tubo no tiene efecto significativo sobre el esfuerzo de flexion debido a la expansión térmica, sino afecta las
fuerzas terminales y momentos en razón directa; por lo tanto los sobresfuerzos no pueden ser remediado por la adicion de grosor; al
contrario, este aumento de grosor tiende a hacer que se comporte peor por el incremento de fuerzas y momento.
4.6
1.
Esfuerzos en un sistema de tuberia
Los esfuerzos de flexión y torsión serán computados usando el modulo de elasticidad de referencia a 70°F , , y entonces
combinado de acuerdo a la ecuación 4.6 para determinar el rango de desplazamiento computado , el cual no excederá el
rango de esfuerzo permisible :
=
Donde
4
(4.6)
= esfuerzo flexor resultante, psi
=
= esfuerzo de torsión, psi
= Momento de torsión, pulg-libra
Z = Modulo de sección del tubo,
El esfuerzo de expansión térmica (ecuación 4.6) esta basado en la teoría del máximo corte.
2.
Los esfuerzos flexores resultantes a ser usados en la ecuación 4.6 para codos y codos fragmentados será calculado de
acuerdo a la ecuación 4.7 , con momentos como los mostrados en la figura 4.2
= esfuerzo flexor resultante =
Donde
(4.7)
= factor de intensificación de esfuerzo en plano de la tabla 4.3 a
= factor de intensificación de esfuerzo fuera de plano de la tabla 4.3 a
= Momento flexor en plano, pulg-lb
= Momento flexor fuera de plano, pulg-lb
Z = Modulo de sección del tubo,
64
3.
Los esfuerzos flexores resultantes a ser usados en la ecuación 4.6 para conexiones ramal, serán calculados de acuerdo
con las ecuaciones 4.8 y 4.9 para los momento que se muestran en la figura 4.3; para cabezales ( piernas 1 y 2 )
Para cabezales ( piernas 1 y 2 ):
=
(4.8)
Para ramales ( pierna 3):
=
(4.9)
Donde
= esfuerzo flexor resultante, psi
= Modulo de sección efectivo para ramal de te,
=π
= radio medio de la sección transversal del ramal, pulg.
= Grosor de pared efectivo del ramal, pulgadas ( menos de y
))
= grosor de tubería que se une a la parte recta de la te del cabezal excepto los elementos de refuerzo, pulg.
= grosor de tubería que se une a la parte del ramal,pulg.
= Factor de intensificación de esfuerzos fuera de plano.
= Factor de esfuerzos en plano.
4.
Rango de esfuerzo permisible
4.2.
y los esfuerzos aditivos permisibles serán computados de acuerdo con la ecuación 4.1 y
Ejemplo 9
Calcular el esfuerzo de torsión, esfuerzo flexor y esfuerzo de expansión en la intersección del cabezal de 4”Ø ced 80 y el
ramal de 3ӯ ced 40 ( fig 4.5 )
Figura 4.5
Esfuerzos en cabezal y ramales.
Los esfuerzos actuando en la intersección se muestran en la tabla debajo:
Cabezal
Cabezal
Ramal
Pierna 1
Pierna 2
Pierna 3
pie - libra
- 550
425
- 180
2 322
1821
- 920
800
- 890
682
65
Solución:
Para el cabezal, “y” es momento torsión, “x” es momento en el plano, y “z” es momento fuera de
plano. Para el ramal, “y” es momento fuera de plano, “x” es momento en plano, y “z” es momento de torsión. Asumir que
una te fabricada no reforzada ( injerto) , es la que da el mas alto numero para SIF.
Ť = 0.337 pulg. ( ver apendice Tabla A4 para 4”Ø ced 80 )
= ( 4.5 - 0.337 ) = 2.082 pulg.
Z = 4.27
h=
Ť
=
.
.
= 0.162
=SIF fuera de plano = 0.9/
= 0.9 / 0.162 = 3.03
=SIF en plano = 0.75 (3.03) + 0.25 =2.52
Para el cabezal pierna 1:
El esfuerzo flexor resultante es:
=
=
.
.
.
=
.
= 9 638 psi
El esfuerzo de torsión :
=
=
=
= 3 262 psi
.
El rango de esfuerzo de desplazamiento computado es:
4
=
=
Para el cabezal pierna 2:
9638
= 13 630 psi
4 3262
El esfuerzo flexor resultante es:
=
=
.
.
.
=
.
= 10 717 psi
El esfuerzo de torsión :
=
=
=
= 2 558 psi
.
El rango de esfuerzo de desplazamiento computado es:
=
4
=
10 717
4 2 558
= 11 876 psi
66
Para el ramal pierna 3:
Ť = 0.337 pulg.
Z = 1.724
= Modulo de sección efectivo para ramal de te,
( ver apéndice Tabla A4 para 3”Ø ced 40 )
=π
= ( 3.5 - 0.216 ) = 1.642 pulg.
= Grosor de pared efectivo del ramal, pulgadas ( menos de
= 0.337 pulg ( Ť y significan la misma cosa )
) = 3.03(0.216) = 0.654 pulg
= 0.337
=π
= π 1.642 0.337 = 2.85
El esfuerzo flexor resultante es:
=
=
.
ó
.
))
=
.
.
= 11 892 psi
El esfuerzo de torsión :
=
=
=
= 2 373 psi
.
El rango de esfuerzo de desplazamiento computado es:
=
4
=
10 892
4 2 373
= 12 804 psi
Dese cuenta que el mismo SIF es usado para el cabezal y el ramal.
4.7
Muelle frio
Un sistema de tubería puede ser tensado en frio o pretensado para reducir la fuerza de anclaje y los momentos causados por la
expansión térmica; el muelle frio puede ser cortado corto para una tubería caliente, o cortado largo para una tubería fría
(criogénica). El corte corto va acompañado por el acortamiento de la longitud total del tubo por la cantidad deseada pero que no
exceda la expansión calculada. El corte largo es hecho para insertar una longitud ( haciendo la longitud del tubo mas larga). La
cantidad del muelle frio (CS) esta expresado como un porcentaje o fracción de la expansión térmica.
Credito para el muelle frio no esta permitido para cálculos de esfuerzo; códigos diferentes estipulan el mismo significado por
ligeramente diferentes palabras. El párrafo siguiente viene del Código Nuclear, Clase 2 tubería NC - 3673 - 3 ASME Sección III:
NC - 3673 - 3 Muelleo frio.
Ningún crédito para muelleo frio esta permitido como consideración a los esfuerzos. En el
calculo de corrimientos y momentos actuando sobre el equipo, las reacciones reales en cualquier tiempo, de preferencia que su
rango serán usadas. El crédito para muelleo frio esta permitido en los cálculos de corrimiento y momentos , convenido el método de
obtención especificado y usado en el diseño del muelle frio.
67
La figura 4.6 muestra la posición de la tubería antes y después del muelle frio (corte mas corto en este caso); la longitud del tubo
es 85 pies en la dirección de la equis y crece 1.54 pulgadas en la temperatura de 300 °F. El porcentaje de muelle frio es 50 %; la
cantidad de longitud a ser recortada es igual al producto del porciento de muelle frio por la expansión real; aquí es o.77 pulgadas.
Por razones practicas, para alcanzar lo mismo en el sitio de construccion se usa un muelle frio de ¾”. Como se puede ver la tubería
es jalada hacia atrás durante la instalación; esto se realiza por fuerza física usando equipos como un tractor. Cuando la tubería se
calienta, cruza la posición neutral y crece hacia el otro lado.
C = Posición instalada ( fría )
H = Posición después instalación ( caliente )
Figura 4.6 Tubería mostrando posición inicial ( fría ) y final C caliente )en el muelle frio.
Las siguientes dificultades han sido encaradas con respecto al muelle frio:
1.
2.
3.
4.
5.
Por error algunos calculan el esfuerzo también con muelle frio, lo cual es erróneo; primero el sistema debiera pasar por los
cálculos de esfuerzo sin consideración del muelle frio ; solamente en el próximo calculo puede ser considerado el muelle frio
para reducir cargas en el equipo.
Algunas veces las cuadrillas de construcción no hacen caso de la necesidad del muelle frio y asi no realizan el muelleo frio.
La cantidad de fuerza necesaria para jalar una línea grande a su posición inicial para soldarla es enorme es enorme.
La reacción en frio a un muelleo frio necesita ser calculada y hecha con la seguridad de que el equipo puede oponerse a esta
carga adicional debida al muelleo frio al principio cuando esta fria.
La localización de las deflexiones en un muelleo frio aun permanecen igual, a causa de que el muelleo frio solo relocaliza el
punto de soldadura y no reduce la expansión real; esta deflexión real es importante en el diseño del muelleo frio; Si no se
satisface la atención, el muelleo puede ser sobredimensionado por la deflexión.
El muelleo frio necesita estar especificado en los puntos de soldadura para ahorrar costos de soldadura adicionales.
Reacciones máxima para Sistemas Simples
( del ANSI B31.3 -2004, párrafo 319.5.1)
Para un sistema de tuberías de dos anclajes sin sujeciones intermedias, los valores máximos instantáneos de las fuerzas de reacción y
momentos puede ser estimado por las ecuaciones 4.12 y 4.13 a.
68
(a)
Para condiciones de desplazamiento extremas,
. La temperatura para este cómputo
reacción, la máxima o mínima temperatura del metal:
=R(1-
)
es la produzca mayor
(4.12)
C= Factor de muelleo frio variando de cero para nada de muelle frio hasta 1 para 100% de muelle frio ( el factor 2/3 esta
basado en la experiencia, el cual nos muestra que el muelleo frio no puede estar completamente asegurado, aun cuando
se elabore con precauciones).Usualmente C de 0.5 se recomienda.
Modulo de elasticidad de referencia a 21 °C(70°F)
= Modulo de elasticidad a la temperatura máxima o mínima del metal
R = Rango de fuerzas de reacción o momentos ( derivados del análisis de flexibilidad) correspondiendo al rango de esfuerzo
de desplazamiento completo y basado sobre .
= Fuerza de reacción máxima instantánea estimada o momento, a la temperatura máxima o mínima del metal.
(b)
Para la condición original,
esta para ser ensamblada.
, La temperatura para este computo, es la temperatura esperada a la cual la
= CR ó
R , cualquiera sea mayor.
tubería
(4.13 a)
Donde la nomenclatura es similar al párrafo anterior y:
=1-
(4.13 b)
= auto-muelleo estimado o factor de relajación; use 0 si el valor de es negativo.
= fuerza de reacción instantánea estimada o momento a la temperatura de instalación.
= Rango de esfuerzo de desplazamiento computado ( de la ecuación 4.6 )
= Esfuerzo caliente, psi.
Reacciones máximas para Sistemas Complejos.
Para sistemas multianclaje y sistemas de dos anclajes con restricciones intermedias, las ecuaciones 4.12, 4.13 a y b no son
aplicables; cada caso debe ser estudiado para estimar localización, naturaleza y extensión de sobredeformaciones y su efecto sobre
la distribución de esfuerzos y reacciones.
Si una tubería esta diseñada con diferentes porcentajes de muelleo frio en varias direcciones, estas ecuaciones no son
aplicables. En este caso, el sistema de tubería será analizado por un método que compendie todo; Las reacciones calientes serán
basadas sobre muelleos fríos teóricos en todas direcciones no mayores que dos tercios de los muelleos fríos tal y como se
especificaron o midieron.
69
Ejemplo 16
Calcular los momentos frio y caliente en la boquilla ( figura 4.7 ) después del 55% de muelleo frio, si el
momento sin muelleo frio fue 2 500 pies-libra del análisis de tubería.
Figura 4.7
Calculo de momento bajo muelleo frio.
El material de la tubería es acero inoxidable A312 TP 304; la temperatura es 900°F. Para calcular la reacción
caliente, use la ecuación 4.12
=R(1-
)
Donde R = momento antes del muelleo frio = 2 500 pies - libra
C = 0.55
= Modulo caliente = 23.4 x 10 psi , a 900°F para acero inoxidable ( apéndice tabla A2 )
= Modulo frio = 28.3 x 10 psi ,
=R(1-
)
=2 500( 1 -
.
)
.
106
.
106
= 2500 ( 0.37) ( 0.8269 ) = 758 pies-libra
Para calcular reacción fría usar la ecuación 4.13 a :
Donde
= CR ó
R , cualquiera sea mayor.
= factor de relajación = 1 -
A causa de que no hubo suficiente información para calcular el rango de esfuerzos de expansión calculado
no podía ser calculado.
La reacción fría,
,el factor
= CR = 0.55 ( 2 500 ) = 1 375 pies-libra
Es importante que la boquilla del equipo debiera soportar no solamente 758 pies-libra en condiciones de operación, sino
también 1 375 pies-libra en una condición fría.
Ejercicios.
1.
Hallar los esfuerzos frios y calientes para tubería de acero al carbón sin costura a - 30°F, 657°F, 1125 °F.:
(a) El material es A53 grado A
(b) El material es API 5 L grado B
2.
Una boquilla de equipo rotativo puede solo soportar una fuerza de 800 libras durante la operación ( figura 4.8 ) y una fuerza
calculada de 3 520 lb……..
………………….
70
usada para reducir la fuerza. ¿ Cual es el porcentaje mínimo de muelleo frio que debiera ser usado ?
3.
4.
5.
6.
7.
8.
Figura 4.8
Ejemplo de muelleo frio
Calcular la fuerza de reacción en el sistema de tubería en acero inoxidable con 65 % de muelleo frio. La temperatura de
operación es 800°F y la fuerza sin muelleo frio es 982 libras.
¿ En que condiciones puede el muelleo frio ser usada ? Enliste las dificultades encontradas con el muelleo frio en teoría y en
la practica.
(a) Calcular el rango de esfuerzos permisibles para tubería A53 grado A a 682°F.
(b) Calcular esfuerzos longitudinales en un codo soldable de 12”Ø de peso estándar, cuando:
Momento flexor en plano = 423 pies-libra
Momento flexor fuera de plano = 325 pie-libra
Fuerza axial = 628 libra
El material es A53 grado A y la temperatura es 682°F.
Calcular SIF y factor de flexibilidad:
(a) Codo 6”Ø radio largo grosor estándar.
(b) Calcular SIF corregido y k , si el codo esta bridado en ambos extremos.
(c) Codo fragmentado con θ= 15° y 12”Ø con un grosor de 0.25 pulg.
(a) Calcular la fuerza de expansión térmica en la tubería mostrada en la figura 4.9; la tubería es 16”Ø ced 80 A53 grado B a
600°F.
(b) Si la distancia entre anclajes se incrementa a 300 pies ¿Cual será la fuerza?
Figura 4.9
Fuerza axial en tubería fija.
Para una tubería sin costura A53 grado B, los esfuerzos permisibles a 70°F y 600°F son 20 000 psi y 17 300 psi,
respectivamente, de acuerdo al Código B31.3. Para un sistema de tubería actual a 600 ° F, los esfuerzos de tubería
computados en ciertas locaciones son como siguen:
(a) El esfuerzo longitudinal debido al peso de presión y otras cargas sostenidas es 9 800 psi.
(b) El rango de esfuerzo de desplazamiento computado es 33 475 psi.
(c) Los esfuerzos debidos a la carga del viento son de 5 822 psi.
¿ Satisface este sistema de tubería el criterio de esfuerzo del código B31.3 ?
71
9.
Calcular el esfuerzo de expansión térmica para el ramal y el cabezal de acuerdo al código ANSI B31.3 para la carga en la
intersección del ramal (dado en el ejemplo 9 y la figura 4.5 ): el ramal y el cabezal son 12”Ø pared estándar y 8”Ø ced 40.
Referencias
1.
2.
3.
4.
5.
6.
7
8.
ANSI B31.1- 1980 Power Piping Code.
ANSI B31.3- 1980 Chemical Plant and Petroleum Refinery Piping Code.
ANSI B31.4- 1974 Liquid Transportation Piping Code.
ANSI B31.8 DOT Gas Transmission transportation Piping Code.
ASME Section III Nuclear components Code.
Markl, Arc
“ Fatige Tests of Piping Components “ Trans. ASME, Vol 74(3), pp 287-303 (April 1952)
Rodabough,E.C. “ Effect of internal Pressure on flexibility and SIF on Curved Pipe” Journal of Applied
Mechanics. Vol 24; Trans. ASME. Vol. 79 ( May 1957 )
Machacek.S.
“ Design and operation of a large Diameter Steam line at Ontario Hydro’s Bruce Nuclear
Power Development “ ASME 78 - PVP - 86
72
CAPITULO CINCO
Espiras de expansión y juntas de expansión
Como se describe en el capitulo 1, dos dispositivos usados para incrementar la flexibilidad de la tubería son las espiras de expansión
y las juntas de expansión. Este capitulo se comprometerá con estos dos tópicos en mas detalle.
5.1
Espiras de Expansión
Las espiras proveen la pierna necesaria de tubería en dirección perpendicular para absorber la expansión térmica; ellas son mas
seguras comparadas con las juntas de expansión, pero toman mas espacio. Las juntas de expansión pueden ser simétricas (figura 5.1)
o asimétricas (figura 5.2). Las espiras simétricas son ventajosas de usar a causa de que la pierna H (figura 5.1) es usada
eficientemente para absorber en igual cantidad la expansión en ambas direcciones; la longitud de curvatura esta dada por:
=W+2(H)
(5.1)
Figura 5.1
Espira simétrica
Figura 5.2
Espira asimétrica
Algunas veces las espiras asimétricas se usan para usar los soportes existentes de acero o para localizar la espira en un cruce de
caminos. Los soportes en dirección vertical se proveen para soportar el peso de la gravedad en el claro calculado como se discute en
el capitulo 3. Las espiras horizontales ( longitud de curva una u otra plana u horizontal) necesitaría un poco mas soportes, cuando se
compara con espiras verticales en la porción de longitud de curva, como se muestra por los soportes
en la figura 5.3. La razón
optima de altura por ancho puede ser estimada o usada.
73
Cuando diversas espiras de tubería yacen lado a lado sobre un puente de tuberías, el tamaño de la espita incluyendo la relación
altura-ancho puede ser modificada para arreglar las espiras una a un lado de la otra como se muestra en la figura 5.3 ; pero el
tamaño final de cada una de las espiras (longitud de curva) debe ser mas grande que la la longitud de curva calculada.
Figura 5.3
Arreglo en planta de muchas espiras.
Las líneas mas calientes y mas grandes se sitúan al exterior como espiras exteriores, a causa de que la altura H necesaria es mas
larga; las líneas mas pequeñas con temperaturas menores se sitúan como espiras interiores; a causa de que este arreglo puede
cambiar el arreglo del puente de tuberías completo, es admisible estimar los tamaños de espira con los cálculos simplificados del
monograma (figura 5.12) en las etapas tempranas del proyecto. Las guías en ambos lado de la espira, como se muestra como y
en la figura 5.3, son importantes para el apropiado funcionamiento de las espiras, a causa de que las guias dirigen la expansión
dentro de la curva a lo largo del eje de tubería, lo cual evita el corrimiento de lado de las líneas. Un problema practico
frecuentemente encontrado es la interferencia cuando no se provee suficiente hueco en el diseño entre tuberías; el hueco, después de
considerar aislamiento en ambas líneas, debiera ser mayor que la expansión diferencial en los codos y como muestra la figura
5.4. Para evitar interferencia, el hueco debe ser > (∆x2 - ∆x1), donde ∆x2 y ∆x1 son las expansiones ocurriendo en la misma
dirección al mismo tiempo.
Vea la figura 5.4 mostrando el hueco requerido y también la consideración de aislamiento.
Figura 5.4
Hueco requerido con ambas líneas calientes.
Precaución debiera ser ejercida en el cálculo de la expansión diferencial, si la espira interior no esta operando y esta a 70°F; en este
caso, el hueco real es menor que el mostrado en la figura 5.5: La figura 5.6 a muestra que sin guías la espira de expansión no se
74
dirige apropiadamente; la figura 5.6 b muestra que la tubería ocupa espacio (conocido como víboras) necesario para el arreglo de
tuberías futuras; esta figura demuestra la necesidad de guias.
Figura 5.5
Hueco requerido, cuando espiras interiores no están operando.
Figura 5.6 (a) Necesidad de guías para controlar la dirección de deflexión.
(b) Puente de tuberías con y sin suficientes guias.
Espiras en tres dimensiones (figura 5.7) son ampliamente usadas debido a que este arreglo no bloquea la ruta de líneas de baja
temperatura debajo de la espira; el alzado usual de altura es cerca de 3 pies. La longitud de curva de la espira es también tomada
aquí como = W + 2 H sin dar crédito para los dos alzados.
5.7
Espiras horizontales en tres dimensiones.
Espiras verticales se sitúan en cruce de caminos y algunas veces son localizadas no simétricamente debido a la localización del
camino; guias verticales pueden ser necesarias para mantener la línea vertical como muestra la figura 5.8
75
Figura 5.8
5.2
Espiras verticales en cruces de caminos.
Esfuerzos y cargas en espiras.
El método de calculo de esfuerzos y cargas en espiras , por M.W. Kellog (referencia 3 en capitulo 1) se sigue.
Ejemplo de cálculo.
Dada una espira de tubo de 20” Diam. Ext. por ½” de grosor ASTM A-135, grado A. L es 20 pies; las guias están localizadas están
localizadas a 10 pies en cada uno de los lados de la espira, de manera tal que L = 40 pies; la distancia entre anclajes A’ y B’ es 100
pies (figura 5.9); la temperatura de la línea es 425°F y es usada para una tubería de aceite. Hallar:
(a) La altura requerida de L.
(b) Las fuerzas actuando en los puntos A’ y B’ y los momentos actuando en los puntos A y B.
Espira de expansión simétrica sujeta a expansión térmica.
Figura 5.9
(a)
Esfuerzos y cargas en una espira simétrica.
La expansio0n térmica lineal unitaria para acero al carbón a 425°F es 0.03 pulg/pie; ∆ = 100 x 0.03 = 3”
pulgadas. = 19 890 ( ignorando permisos de código para excluir eficiencia de la junta longitudinal)
∆
=0.0531
Entre a la figura 5.10 con 0.0531 Lea sobre la curva representando
0.32 ; L es por lo tanto 40 x 0.32 = 12.8 pies.
= 0.5 y bajar hasta que el valor de K sea
76
Multiplique L por
y
para obtener las dimensiones de la espira.
Figura 5.10
Diseño de espiras usando la carta de M. W. Kellog.
77
Figura 5.11
Momentos y fuerzas en una espira usando la carta M.W. Kellog.
78
´=-
´ = - 10
∆
(5.2)
=-
= - 10
∆
(5.3)
(b) El momento de inercia para 20” pulg. De Diámetro externo x ½” de grosor de tubo = 1 457
∆
=
∆
= 0.0683
=
= 2.73
Entrar en la figura 5.11 con = 0.5 y = 0.32
Leer
= 0.55
= 0.86
´=-
=-
´ = 0.0683 x 10
x 0.55 = 37 600 libras (usando la ecuación 5.2)
= 2.73 x 10 x 0.86 = 235 000 pies-libras (usando la ecuación 5.3)
Figura 5.12
Nomograma para determinar el tamaño de espira
79
El nomograma presentado en la figura 5.12 puede ser usada para estimar el tamaño de la espira de expansión. Fuera de los cuatro
arreglos de espiras de expansión en un plano simple mostrados, el tipo A es popular debido a al facilidad de fabricación usando codos
estándar y tramos de tubería recta. Los otros arreglos requieren que la tubería se doble a una configuración específica.
En el alcance de el nomograma, se asumió lo siguiente:
La formula usada es la del cantiléver guiado dada por la ecuación 1.3
La pierna requerida es :
Donde:
L=
∆
( 1.3 )
= 20 000 psi
E = 29 x 10 psi
∆= expansión a ser absorbida por la espira, pulgadas.
D = Diametro nominal, pulg ( note que la ecuación 1.3 usa el diámetro exterior)
L = Distancia entre guias, pies.
= Distancia entre anclajes, pies.
= Longitud de curva requerida para absorber la expansión, pies.
Ejemplo 1
Hallar el tamaño de la espira para absorber la expansión en 200 pies de un tubo de 12”Ø de acero al carbón a 400°F; Asumir la
relación altura a ancho.
Expansión total = 200 (0.027) = 5.4 pulg
Usando el nomograma y asumiendo una línea recta comenzando desde un diámetro de 12” y a través de 5.4 pulg de
expansión, se lee una longitud de curva como 50 pies; Asumir que H = W, entonces = 2H + W = 50 pies.
Así, H = W = 17 pies, haciendo que = 51 pies
Por calculo
L=
∆
=
106
.
= 44 pies
El tamaño de espira estimado esta dado en la figura 5.13
Figura 5.13
Tamaño de espira estimado usando nomograma.
Ejemplo 2
Usando el método de Kellog, calcular esfuerzo, fuerza, y momento en la espira de expansión mostrada en la figura 5.14. El diámetro
de tubería es 6”Ø ced 40, la temperatura es 450°F y es tubería de acero al carbón. Usar las figuras 5.10 y 5.11 para alcanzar la
80
solución. Este problema es el mismo para el cual los resultados se presentaron en el capitulo 1, tabla 1.3. Aquí el problema esta
solucionado paso por paso.
El coeficiente de expansión para acero al carbón a 450°F = 0.0316 pulg/pie ( apéndice A1)
Figura 5.14
Constante
=
= 0.5 y
Para
Calculo de esfuerzo y cargas usando el método de Kellog.
=
=
= 0.5
= =
=
= 0.5
= 0.5 , de la figura 5.10, leer
∆
como 0.03
=½(L)(1= ½ ( 40 ) ( 1 - 0.5 = 10 pies
∆ = deflexión= 200 ( 0.0316 ) =6.32 pulg
OD = 6.625 pulg
S =esfuerzo =
.
∆
=
.
.
.
Momentos y fuerzas
Usando la figura 5. 11 , se lee:
Donde
= 0.21
= 0.5
I = 28.14
Fuerza axial en el anclaje ( ecuación 5.2 ):
´=-
´=-
∆
=-
= 7 850 psi
= 0.5
= 0.5
.
.
.
.
= 584 libras
Momentos en la guias ( ecuación 5.3 ):
=-
Nota:
=-
∆
=
.
= 5 558 pies - libras
El primer subíndice denota dirección, el segundo subíndice denota localización , los signos son aquellos de las
fuerzas y momentos actuando sobre los anclajes ( ver figura 5.15 ).
81
Figura 5.15
5.3
Coordenadas usadas.
Juntas de expansión
En 1984 las juntas de expansión fueron permitidas en el diseño de tuberías nucleares excepto para el Código ASME Sección III. La
subseccion NB -3671.2 estipula que las juntas de expansión no están permitidas en la clase NB de componentes nucleares. Accidentes
en el pasado con juntas de expansión son una preocupación desde el punto de vista de seguridad; las juntas de expansión se usan
para absorber la compresión axial o la extensión del descentrado lateral y la rotación angular. Tal y como dice los estándares de los
manufactureros de las juntas de expansión ( referencia 1 ), la rotación torsional debiera ser evitada sobre el fuelle debido a que el
torque produce altos niveles de esfuerzos en el fuelle.
Las juntas de expansión pueden ser clasificadas de una manera amplia como deslizantes y flexibles. Hay un movimiento relativo de
partes adyacentes en el caso de juntas deslizantes; las juntas resbaladiza, juntas giratorias y juntas de bola están agrupadas bajo las
juntas deslizantes. Los coples Dresser y coples Victaulic son unos de los nombres de marca de las juntas de este tipo. Las juntas
deslizantes son también llamadas juntas empacadas, a causa de que el empaque contiene la presión interna sin fugas si es necesario.
Las juntas de expansión flexibles pueden ser divididas adicionalmente en: Juntas de fuelle, mangueras metálicas, y tubería corrugada
(referencia 2 y 3).
Figura 5.16 Tipos de juntas de expansión (Estándares de la Asociación de Manufactureros de Juntas de Expansión)
82
Los siguientes son términos usados en el diseño y especificación de las juntas de expansión ( ver figura 5.16 para los símbolos usados
para algunos de los términos ):
Anclaje principal: Un anclaje principal debe ser diseñado para resistir las fuerzas y momentos impuestos sobre cada una de las
secciones de tubería para las cuales el anclaje es implementado. En el caso de una sección de tubería conteniendo
una junta de expansión, las fuerzas y momentos consistirán del corrimiento debido a la presión (ecuación 5.4),
flexionar la junta de expansión (ecuación 5.5), y las fuerzas de fricción debidas al alineamiento de la tubería en las
guías y soportes. Cuando un anclaje principal esta instalado en el cambio de dirección de flujo, el efecto en el codo
del empuje centrifugo debido al flujo (ecuación 5.6) debe también ser considerado.
Anclaje intermedio: Un anclaje intermedio divide una línea de tubería , en secciones de tubería expandiéndose individualmente, cada
una de las cuales es hecha flexible a través del uso de una o mas juntas de expansión.
Anclaje direccional: Un anclaje direccional o anclaje deslizante, es uno diseñado para absorber la carga en una sola dirección,
mientras que permite el movimiento en otra dirección.
Fuelle:
El elemento flexible de una junta de expansión, consiste de una o mas corrugaciones y las tangente, si hay alguna.
Material del fuelle: Una lista de materiales metalicos prar fuelles es dada a continuación:
Material del fuelle
Acero inoxidable 304
Acero inoxidable 316
Acero inoxidable 321
Acero inoxidable 347
Niquel 200
Monel 400
Inconel 600
Inconel 625
Incoloy 800
Incoloy 825
Rango de Temperatura °F
( especificado por ASME Sección VIII)
- 300 a 750
- 300 a 750
- 300 a 1 500
- 300 a 1 400
- 300 a 600
- 300 a 900
- 250 a 1 200
- 250 a 1 200
- 250 a 1 500
- 250 a 800
Retorcimiento(serpenteo) en una junta de expansión de fuelle: Un termino empleado para denotar el acontecimiento de mutabilidad
debido a la presión interna y es predominantemente asociada con juntas de 20 “ ó mas pequeñas.
83
Flexibilidad de una junta de expansión: Esta puede ser incrementada por: fuelles mas delgados ( debe además poder resistir la
presión) , incrementar el numero de arrugas, y por fuelles multiples.
Cubierta externa: Una cubierta usada para proteger el exterior del fuelle de los objetos extraños, especialmente cuando la junta esta
sepultada debajo de la tierra.
Recubrimiento interior o camisa , se usa para lo siguiente:
1.
Donde es necesario para minimizar las perdidas por fricción.
2.
Donde las velocidades de flujo son altas ( para líneas de vapor con velocidades que exceden los 1 000
pies/min/pulgada de diámetro, en líneas hasta 6”Ø)
3.
Cuando están presentes materiales abrasivos.
4.
Cuando hay retrocesos o fluo turbulento.
5.
Para todas las aplicaciones de alta temperatura.
6.
Para todos los codos de cobre.
Cuando flambeo lateral o rotación esta presente, la camisa debe ser lo suficientemente pequeña en diámetro para
proveer el claro necesario.
Varillas de tensión: Estas son dispositivos de varillas o barras con el propósito de fijar la junta de expansión del corrimiento debido
a la presión interna. El numero y tamaño de las varillas depende de la magnitud de las fuerzas de empuje; estas
varillas también pueden actuar como varillas limitadoras de flambeo.
Anillos reforzadores o igualadores: Estos ayudan a reforzar los codos contra la presión interna y mantener el perfil deseado de los
codos.
Guías:
Las guías son partes importantes del desempeño de las juntas de expansión.
5.4
Tipos de juntas de expansión ( ver figura 5.16 )
Junta de expansión simple: La forma mas simple de junta de expansión, de construcción en un solo fuelle, diseñada para absorber
todo el movimiento de la sección de tubería en la cual esta instalada.
Junta de expansión doble: Una junta de expansión doble consiste de dos fuelles reunidos por un conector común el cual esta anclado
a alguna pate rígida de la instalación por medio de una base de anclaje. La base de anclaje puede ser conectada al
conector común en la instalación o cuando se manufactura. Cada fuelle actúa como una junta de expansión simple,
y absorbe el movimiento de la sección de tubería en la cual esta instalada, independientemente de las otros fuelles.
Las juntas de expansión dobles no debieran ser confundidas con las juntas de expansión universales.
84
Juntas de expansión guiadas internamente: Una junta de expansión guiada internamente esta diseñada para proveer guía axial
dentro de la junta de expansión por la incorporación de una camisa guía pesad telescópica interna, con o sin el uso
de anillos de apoyo. ( Nota: el uso de una junta de expansión internamente guiada, no elimina la necesidad del uso
de adecuadas guías externas de tubería).
Junta de expansión Universal: Una junta de expansión universal contiene dos fuelles en un conector común para el propósito de
absorber cualquier combinación de los tres movimientos básicos, esto es, el movimiento axial, la deflexión lateral,
y la rotación angular. Las juntas de expansión universal son usualmente compradas con varillas limitadoras, para
distribuir el movimiento entre los dos fuelles de la junta de expansión y estabilizar el conector común. Esta
definición no implica que solo una junta de expansión de doble fuelle pueda absorber el movimiento universal.
Junta de expansión articulada(de bisagra): Una junta de expansión articulada contiene unos fuelles y esta diseñada para permitir
rotación angular en un plano solo por el uso de un par de pasadores a través de las cuales se articulan las placas
adicionadas a las terminales de la junta de expansión. Las bisagras y los pasadores de la bisagra deben ser
diseñados, donde se aplican, para sujetar el empuje de la junta de expansión debido a la presión interna y fuerzas
extrañas. Las juntas de expansión articuladas debieran ser usadas en conjuntos de dos o tres para funcionar
apropiadamente.
Junta de expansión giratoria: Una junta de expansión giratoria esta diseñada para absorber deflexión lateral y/o rotación angular
en un plano; el empuje de presión y las fuerzas extrañas son sujetadas por el uso de un par de barras giratorias,
cada una de las cuales esta articulada a los extremos de las juntas de expansión.
Junta de expansión cardan: Una junta de expansión cardan esta diseñada para permitir rotación angular en cualquier plano por el
uso de un par de bisagras fijadas a un anillo cardan flotante común. El anillo cardan, las bisagras y los pasadores,
donde se aplican, deben ser diseñados para sujetar el empuje de la junta de expansión, debidos a la presión interna
y fuerzas extrañas.
Juntas de expansión de presión balanceada: Una junta de expansión de presión balanceada esta diseñada para absorber movimiento
axial y/o deflexión lateral, mientras que sujeta el empuje de presión por medio de artificios de tirantes
interconectado los fuelles de flujo con un fuelle opuesto también sujeto a la presión de la línea. Este tipo de junta
de expansión se usa normalmente donde un cambio de dirección en la ruta de una tubería. El extremo de flujo de
una junta de expansión de presión balanceada, algunas veces contiene dos fuelles separados por un conector
común, en tal caso se llama junta de expansión de presión balanceada universal.
85
5.5
La fuerza estática
Fuerza de empuje de presión.
debida a la presión interna esta dada por la ecuación 5.4:
= ap
(5.4)
Donde a = área efectiva correspondiente al diámetro medio de las corrugaciones,
p = Presión de diseño de la línea basada en la condición mas severa, psi
La fuerza requerida para comprimir la junta de expansión en la dirección axial
es:
= ( constante de muelleo axial)( cantidad de compresión)
El desplazamiento centrifugo
en el codo debido al flujo esta dado por :
=
(5.5)
sen
(5.6)
Donde A = Área interna del tubo,
ρ= Densidad del fluido,
V = Velocidad de flujo, pie/seg
G = Aceleración debida a la gravedad = 32.2 pie/
Θ= Angulo de curva.
La figura 5.17 muestra el codo donde un anclaje principal esta localizado. El diseño de la fuerza de anclaje debiera incluir el empuje
de presión, empuje centrifugo, fricción en soportes y guías, y la fuerza para comprimir los fuelles.
Figura 5.17
Fuerza de anclaje en el codo.
Ejemplo
Usando la ecuación EJMA (referencia 1) , calcular la presión de prueba hidrostática si la presión de diseño es 125 psig, y la
temperatura de diseño es 500°F. El material del fuelle es acero al carbón ASTM A53 grado B.
La presión de prueba es: ( usando la ecuación 2.7)
= 1.5
Donde
= Presión de diseño = 125 psig
= Esfuerzo permisible del material del fuelle a la presión de prueba (70°F)= 20 000 psi ( del apéndice A3)
= Esfuerzo permisible del material del fuelle a la temperatura de diseño de 500°F=18 900 psi ( del apéndice A3)
86
Así,
= 1.5
= 1.5
= 198.4 psig
Ejercicios
1.
(a) El tamaño de la espira de expansión para las siguientes condiciones:
Diámetro = 16”Ø peso estándar
Material = A53 grado A
Distancia entre anclajes = 220 pies
Peso/pie de longitud de tubería = 80 libras/pie
Temperatura = 750°F
Claro = 25 pie
(b) Calcular la fuerza de anclaje para zapatas con placa deslizante de teflón.
(c) Calcular la fuerza en las guias.
2.
(a) Diseño de la espira de expansión, por ecuación, con una espira con relación alto-ancho igual a 1.
Distancia entre anclajes = 225 pies
Temperatura = 800°F
Claro = 20 pies
Diámetro = 12”Ø peso estándar
Material = A53 grado B
(b) Calcular la fuerza en los anclajes para zapatas con acero sobre acero
(c) Calcular la fuerza en las guias.
3.
(a) Calcular la expansión térmica en A y B en el sistema de tubería dado en la figura 5.18; el material es A106 grado B a
750°F.
Figura 5.18
Espira
(b) Cual de las siguientes es mas ventajosa de usar en la figura anterior: (1) ¿espira de expansión simétrica? (2) ¿ espira de
expansión asimétrica ?
87
4.
La dimensión de una espira de expansión esta limitada a como se muestra en la figura 5.19, Si una tubería tiene una
temperatura de de 650°F, ¿ cuantas espiras de expansión requiere para 500 pies de longitud de tubería ?
Figura 5.19
5.
Si una línea esta anclada en ambos extremos, pero los anclajes tienen movimientos térmicos como los mostrados en la figura
5.20, ¿ Cual es el tamaño de la espira ? Es una tubería de 4”Ø ced 80 acero al carbón A53 grado B a 350°F.
Figura 5.20
6.
Numero de espiras.
Tamaño de espira
Una espira de 6”Ø de tubo cedula estándar acero A53 grado B con temperatura de operación de 375°F.
Para la espira mostrada en la figura 5.21: (a) hallar la fuerza resultante F en los anclajes, (b) Hallar el momento M en los anclajes.
Figura 5.21
Espira
7.
Tamaño de la espira de expansión basada sobre las siguientes condiciones: un tubo de 12”Ø ced 40 A53 grado B ; la
temperatura es 350°F, el ancho de espira es 8 pies; y la longitud del tubo es 180 pies.
8.
Del catalogo de manufacturero hallar la longitud total de manguera flexible necesaria para ± ½” de descentrado de
flambeo para una manguera de diámetro interno de 6”Ø. Asumir el tipo de conexión en el extremo.
9.
Una tubería de 12”Ø peso estándar acero al carbón esta a 525°F; la presión de diseño es 180 psig. Con una junta de
expansión simple de fuelle en el sistema de tubería como en la figura 5.22, ¿ calcular las fuerzas en la boquilla y el anclaje?
El área media del repliegue es 151
; la tasa de muelleo axial es 882 lb/pulg.
88
Figura 5.22
10.
Junta de expansión
Una turbina de 40” de diámetro de un sistema de ductos de extracción esta fabricada de una pared de 5/8” de acero al
carbón, y opera a un vacio completo a 320°F. El movimiento en el brida de extracción de la turbina y la entrada al
condensador esta determinado como se muestra en la figura 5.23. Una junta de expansión de presión balanceada universal
esta localizada entre dos piezas del equipo con las dimensiones mostradas en la fig 5.23. Determine las fuerzas y momentos
debidos a las rigideces del fuelle en las conexiones del condensador y la turbina. Los datos suministrados por el
manufacturero de la junta de expansión son los siguientes:
Diametro medio del fuelle = 42 pulg
Tasa de muelleo de trabajo = 32 000 lb/pulg/ pliegue
Numero de pliegues del fuelle de flujo = 6 + 6
Numero de piegues del fuelle balanceante = 6
Figura 5.23 Junta de expansión de presión balanceada universal.
11.
Una junta de expansión de fuelle simple esta situada en una tubería de 20”Ø de acero al carbón que corre entre los anclajes
A, B, C. En el punto de anclaje B esta una guía direccional que restringe solo el movimiento axial. La línea esta operando a
150 psig y 550°F; las longitudes de tubería se muestran en la figura 5.24. ¿ cuales son las fuerzas y movimientos actuando
en A, B, C ? . Los datos proporcionados por el manufacturero de juntas de expansión son:
El área efectiva correspondiente al diámetro medio del fuelle = 480
Diámetro medio
= 21.5 pulg
Longitud libre del fuelle = 12 pulgadas
Numero de pliegues N = 12
89
Referencias
1.
2.
3.
Expansion Joint Manufacturers Association 1973 Addenda to Standars of EJMA. 3rd ed, 1969.
Robert L. Benson, Chemetron Corp “ A Basic to Analyzing Piping Flexibility” Chemical Engineering ( Oct 23, 1973 )
Engineering data on expansion joints are available from ( company or trade name ); Pathway, Flexonics, Adsco, Solar,
Anaconda, Temp Flex, Tube turns, Zallea Bros, and Metall Bellows.
90
CAPITULO SEIS
Juntas bridadas.
Las bridas se usan para reunir secciones de longitudes de tuberías, y para conectar tubería a equipos. Los dos principales tipos de
bridas son de cara plana o cara realzada. En el análisis de esfuerzo de tubería, la capacidad de una brida para conducir momento
externo es de una importancia conocida. El diseño real de una junta bridada puede ser obtenido de otras fuentes ( referencias 1 y 2 ).
Los efectos de la precarga del tornillo, presión, temperatura, y momentos externos se discuten a continuación.
Precarga del tornillo:
El apriete inicial del tornillo es una operación de pre-esfuerzo; la cantidad de esfuerzo desarrollado del
tornillo debiera ser suficiente para soportar contra toda condición esa tendencia a producir fugas en la
junta, y al mismo tiempo no ser tan excesiva que la deformación del tornillo o bridas puedan producir
relajación que pueda también resultar en fugas; por eso, para que la junta sea hermética bajo presión
hidrostática ( una y media veces la presión de diseño ), puede ser permisible un esfuerzo inicial en
tornillos mas alto que los esfuerzos de diseño.
Presión interna:
Cuando se aplica presión interna, cedencia adicional del tornillo puede causar fugas, si el margen entre el
esfuerzo inicial del tornillo y el esfuerzo de cedencia es menor.
Presión externa:
La fuerza combinada del momento de flexión externó y la carga del tornillo, pueden plásticamente
deformar ciertos empaques lo que resulta en perdida de la presión del empaque cuando la conexión es
despresurizada.
Temperatura:
El incremento en la temperatura reduce la presión a la cual la brida puede estar sujeta. En temperaturas
elevadas, los valores de esfuerzo de diseño están gobernados por una tasa de deslizamiento. Si el
coeficiente de expansión térmica es diferente (diferente material) para la brida y el tornillo, la fuga puede
ocurrir debido al incremento en la carga del tornillo; entonces el reapriete del tornillo puede ser
necesario, pero no debe ser olvidado que los efectos de reaprietes repetidos puede ser acumulativo y
puede deformar el empaque y causar fugas.
6.1
C
Nomenclatura
Esfuerzo de cedencia del material de la brida, psi
Diámetro del circulo de tornillos de la brida, pulg.
Área total de sección transversal del área de tornillos en la raíz de la rosca,
Diámetro exterior de la cara realzada de la brida
91
PR
G
Presión concurrente con el momento flexor bajo la carga dinámica
Diámetro de localización de la reacción de carga del empaque, pulg ( puede ser aproximado al diámetro interior de la cara
realzada de la brida ).
Esfuerzo permisible del tornillo, psi.
Unidades:
Momentos
pies-lb
Esfuerzos
psi
OBE Terremoto base operante
SSE
terremoto paralizante de seguridad
SAM
Movimiento de anclaje sísmico
Las condiciones de falla están asociadas con el SSE ó ruptura de tubería; es un evento extremadamente poco probable.
LOCA( Loss of coolant accident ) El accidente de perdida de refrigerante, el resultado sería una apertura inadvertida de la válvula de
alivio o seguridad presurizada, a causa de la perdida de refrigerante superando la capacidad del sistema de recuperación de
refrigerante del reactor.
6.2
Momentos externos
El efecto de los momentos externos será discutido en detalle. Los momentos permisibles pueden ser calculados, por los tres métodos
resaltados por el código ASME sección III, Componentes de plantas nucleares de potencia NC - 3658.
Método 1: Este se refiere a al ANSI B16.5 para juntas bridadas con tornillos de alto esfuerzo ( el material del tornillo con esfuerzos
permisibles a 100°F no menores que 20 000 psi.
(a)
Para niveles de servicio A y B bajo cargas estáticas dado por la ecuación 6.1
(b)
Para niveles de servicio A y B bajo cargas estáticas y dinámicas dadas por la ecuación 6.2
(c)
Para niveles de servicio C y D bajo cargas estáticas y dinámicas dadas por la ecuación 6.3
Método 2: Este método atañe a juntas bridadas estándar a rangos de presión modernos, y temperaturas de estándares ANSI B16.5,
MSS SP - 44, API 605 ( presiones menores que 100 psi y temperaturas menores que 200°F )
Método 3: Este es el método de presión equivalente .
Los límites de servicio de los niveles A y B deben ser satisfechos para todas las cargas identificadas en la especificación de diseño en
el desempeño de su función de servicio especificada. El componente o soporte debe resistir estas cargas sin daño que requiera
reparación.
92
Los limites de servicio de los niveles C y D permiten grandes deformaciones en areas de discontinuidad estructural; la ocurrencia de
este tipo de suceso, ocasionaría la necesidad de remoción del componente del servicio, para inspección o reparación del daño al
componente o soporte.
6.3
Comparación de momentos permisibles y reales
Método 1: ( Opción de atornillado de alto esfuerzo ) los limites de diseño y limites de niveles de servicio A y B son:
= 3 125
donde
C
(6.1)
no debiera ser mayor que la unidad.
( para niveles A o B )= 6 250
C
(6.2)
Como se puede ver, los resultados de la ecuación 6.2 serán el doble que los de la ecuación 6.1
Los limites de diseño y limites de niveles de servicio C y D ( fallas ) son:
( para niveles C o D )= [11 250
(6.2)
Método 2: ( Para bridas a presiones y temperaturas moderadas )
=
=
C
(6.4)
C
(6.5)
Método 3: ( Método de presión equivalente )
=
(6.6)
Donde M es el momento mas grande ( real ) calculado de las bridas bajo este método de las ecuaciones 6.7 , 6.8 , y 6.9.
mas la presión de diseño debiera ser menor que la presión estimada en 6.6.b
93
Momentos reales
M ( normal ) =
= el mas alto de los dos momentos flexores el torsional o el resultante para la gravedad mas la
carga térmica normal, el movimiento de anclaje sostenido mas la fuerza de desplazamiento de la vcalvula de alivio
y otras cargas sostenidas mecánicas.
(6.7)
M ( realzado )=
= el mas alto de los dos momentos flexores el torsional o el resultante mas el realce térmico,
mas OBE, mas SAM mas LOCA.
(6.8)
M ( de falla )=
= el mas alto de los dos momentos flexores el torsional o el resultante mas el
realce térmico, mas SSE, mas SAM, mas LOCA
(6.9)
M = El mayor de los tres momentos reales de arriba
Este momento será usado para obtener la presión equivalente.
(6.10)
Como puede ser esperado, para la aprobación del uso de la brida en ciertas locaciones, los momentos flexores reales o calculados
deben ser mas bajos que los momentos permisibles. La tabla 6.1 da los números de ecuación para los momentos reales y los
permisibles para su comparación.
Tabla 6.1
Reales
M ( normal ) ( ecuación 6.7 )
M ( realzado ) ( ecuación 6.8 )
M ( de falla ) ( ecuación 6.9 )
M ( normal ) ( ecuación 6.7 )
M ( realzado ) ( ecuación 6.8 )
M ( de falla ) ( ecuación 6.9 )
+ presión de diseño ( ecuación 6.6 a )
Empaques:
Comparación de momentos reales contra permisibles
Permisibles
( ecuación 6.1 )
( ecuación 6.2 )
( ecuación 6.3 )
( ecuación 6.4 )
( ecuación 6.5 )
( ecuación 6.6 )
Presión esperada
La sección NC - 3647.5 permite solo empaques metálicos o de asbesto, si la presión de servicio normal excede 720
psi ó la temperatura excede 750°F. Sin embargo, Los empaques de hojas de asbesto comprimido confinado no están
limitados tal y como para presión suministrada, sino el material del empaque es apropiado para la temperatura
Problema ejemplo
Calcular los momentos real y permisible y revisar , si la brida dada esta calificada de acuerdo al ASME Sección III, NC
- 3658 (verano 1979)
Diametro tubo = 30ӯ
El diámetro exterior de la cara realzada de la brida = 33.75 pulg
94
Numero de tornillos = 28
Área total de tornillos = 28 ( 0.8898 ) = 24.94
Diámetro del circulo de tornillos C = 36 pulg
El material de la brida es acero al carbón SA 105
El material del tornillo es SA 193 grado B7
Esfuerzo permisible del tornillo = 25 000 psi
Esfuerzo de cedencia del material de la brida
= 32 800 psi
Rango de presión = 150 psi
Temperatura de diseño = 200°F
Presión de diseño = 175 psi
Los momentos reales ( lb - pie )del análisis de tubería están dados en la tabla 6.2
El mas altos de los momentos torsional ó flexor resultante esta tabulado en la tabla 6.2 . Las ecuaciones 6.7, 6.8, y 6.9 se usan para
calcular el momento rea para condiciones normal, realzada y de falla.
Tabla 6.2
Carga
Peso muerto
Termico
OBE
OBE SAM
SSE
SSE SAM
LOCA
M ( normal ) =
M ( realzado )=
M ( de falla )=
Momentos reales del análisis de tubería ( pie - libra )
B
1 084
1 901
8 518
0
18 354
0
0
B
1 939
6 350
7 979
0
16 638
0
0
B
11 520
2 825
9 817
0
10 448
0
0
B
El mas alto de
+
11 682
6 950
12 650
0
19 646
0
0
11 682
6 950
12 650
0
19 646
0
0
= 11 682 + 6 950 = 18 632 pie - lb ( de la ecuación 6.7 )
= 11 682 + 6 950 + 12 650 = 31 282 pie - lb ( de la ecuación 6.8 )
= 11 682 + 6 950 + 19 646 = 38 278 pie - lb ( de la ecuación 6.9 )
Momentos permisibles
El material de tornillos es SA 193 grado B7 de aleación de acero con esfuerzo permisible de 25 000 psi.
El método 1, conocido como la opción de alto esfuerzo, se usa a causa de que el esfuerzo permisble del tornillo es mayor que 20 000
psi a 100°F. En este caso se usan las ecuaciones 6.1, 6.2 y 6.3 para calcular los momentos permisibles
95
= 3 125
( 24.92 ) = 212 858 pies - libra
(6.1)
=2 ( 212 858 ) 425 716 pies - libra
= 11 250 24.92
(6.2)
33.75
175
.
=
= 659 310 pie-libra
(6.3)
La tabla 6.3 nos da la comparación de momentos para el ejemplo problema.
Tabla 6.3 Comparación de momentos ( pie - libra )
Condición
Normal
Realzado
De falla
Momento real
18 632
31 282
38 278
Permisible
212 858
425 716
659 310
Momento
OK
OK
OK
El efecto del material de la brida, rango de la brida, y diámetro de brida, sobre el momento permisible se muestra en la tabla 6.4 . La
presión interna de la brida es 175 psi. Como era esperado los momentos permisibles son mas altos para bridas mas grandes y mas
altos rangos. Los momentos permisibles para bridas de acero al carbón son mas altos que para bridas de acero inoxidable, a causa de
que los esfuerzos de cedencia (usados en la opción de atornillado de alto esfuerzo) para acero al carbón son mas altos; el esfuerzo de
cedencia para acero al carbón es de 32 800 psi comparado con 21 300 para acero inoxidable ambos a 200°F.
La temperatura usada es 200° F y la presión es 175 psi.
Tabla 6.4
Momentos permisibles de bridas ( pie - libra ) Usando el método 1.
Referencias
1.
2.
3.
4.
5.
6.
Código ASME Sec III, Div 1.”Nuclear Power Plant Components” Article XI - 3 000
Código ASME Sec III, Div 1. “Design of Flanged Joints “ Appendix II.
Código ASME Sec III, Div 1.”Nuclear Power Plant Components” subsection NC3658 (summer 1979)
“Flange Qualification Programs” Tennessee Valley Authority.
ANSI B16.5 “Steel Pipe Flanges and Flanged Fittings” (1977)
API 605 Reaffirmed in 1973, “ Large Diameter Carbon Steel Flanges”
96
CAPITULO SIETE
Tubería conectada a equipo no rotatorio.
Las cargas externas impuestas sobre equipo no rotativo por una tubería, debiera estar por debajo de las cargas permisibles
proporcionadas por los manufactureros. Ejemplos de equipos sin fuego como intercambiadores de calor, tanque, tambor colector,
Recipientes a presión, enfriadores de aire, y condensadores. Ejemplos de recipientes a fuego son los calentadores y calderas a fuego.
Las fuerzas reales y momentos de un análisis de esfuerzo de tubería puede ser enviado a los manufactureros para que den un
aprobación de estas cargas.
Los métodos para calcular esfuerzos locales sobre el recipiente y la interacción con la boquilla, son:
1.
2.
3.
Análisis de elemento finito que es el mas acucioso pero que podía ser caro por sus recursos de computación.
Calculo de esfuerzo local delineado en forma destacada por Weldin Research Council ( WRC ) boletín 107 (referencia 1)
WRC boletín 297, (referencia 8) Esfuerzo local en cubiertas cilíndricas, suplemento del boletín 107 de WRC.
Para cada pieza del equipo, los estándares y códigos aplicable debieran ser satisfechos. Presentamos aquí una discusión con ejemplos
para recipientes cilíndricos y esféricos, en lugar de una copia del texto asequible de otras fuentes.
7.1
Calculo de esfuerzo local usando el boletín 107 de WRC
El WRC 107 fue preparado basándose en un trabajo realizado por Bijlaard. Las convenciones de signo usadas son exactamente como
las dadas en el boletín.
1.
El rango de relación del diámetro del recipiente(cilíndrico) entre el grosor es 10 ≤ ≤ 600.
2.
El rango de relación diámetro de la boquilla entre diámetro del recipiente es 0.02 ≤ ≤ 0.57
3.
4.
El grosor de la boquilla no esta considerado para recipientes cilíndricos.
La lectura de las constantes no-dimensionales del boletín WRC 107 son solo para rangos aceptables; la extensión de las
curvas pueden ser usadas solo si es permitido. Los valores fuera de rango pueden dar resultados poco conservadores.
La revisión de marzo de 1979 nos da revisiones importantes; versiones anteriores se deben usar con mucho cuidado.
Los signos para los esfuerzos fueron obtenidos de la consideración de la deflexión resultante de la cubierta de varios modos
de carga. El esfuerzo tensor esta marcado como +, y el esfuerzo de compresión esta marcado como -.
La teoría de máximo corte ha sido usado para determinar la intensidad de esfuerzo.
El WRC 107 omite el esfuerzo de presión interna. El efecto de la presión puede ser incluido si se desea.
Los esfuerzos calculados están en la pared del recipiente ( cubierta ) y no en la boquilla; los esfuerzos pueden ser mas altos
en la pared de la boquilla , en caso de que la abertura de la boquilla no este reforzada.
El método WRC 107 puede ser usado para tapas elipsoidales, tan bien como en cubiertas cilíndricas y esféricas.
5.
6.
7.
8.
9.
10.
97
11.
12.
Los esfuerzos debidos a la carga radial en cubiertas cilíndricas no es aplicable, si la longitud del cilindro es menor que su
radio. Las curvas son para relaciones radio-longitud de 8.
Los esfuerzos debidos a momentos externos no son aplicables, si el accesorio esta localizado dentro de la distancia de la
mitad del radio de la cubierta del extremo cercano de la pared.
La tabla 7.1 nos da los factores de concentración de esfuerzos
y
. Las ecuaciones para calculo de los factores de
y
se dan en las ecuaciones 7.1 y 7.2. La tabla 7.1 fue generada usando estas ecuaciones.
concentración de esfuerzos
Tabla 7.1 Factores de concentración
T ( pulgadas)
3
8”
7
16”
1
2”
9
16”
5
8”
11
16”
3
4”
7
8”
( Basados sobre radios de 3 8” en la interface cubierta a boquilla )
1
11
8”
1 1 4”
1 1 2”
1 3 4”
2“
1.5121
1.5661
1.6174
1.6665
1.7138
1.7594
1.8036
1.8882
1.9688
2.0459
2.1200
2.2609
2.3938
2.5202
1.2899
1.3280
1.3650
1.4010
1.4363
1.4709
1.5048
1.5771
1.6355
1.6983
1.7597
1.8790
1.9943
2.1064
Los esfuerzos reales calculados son comparados con los esfuerzos permisibles. Si el esfuerzo real es mas alto, un grosor de refuerzo
se asume, y el calculo se vuelve a correr con el grosor total( suma del grosor del recipiente y el refuerzo) como grosor . En la
practica, el grosor asumido de refuerzo es igual al grosor del recipiente; si el doble del grosor no es suficiente, los esfuerzos deben
enfocarse en reducir cargas sobre el recipiente.
Para carga de membrana,
=1
Para flexión,
=1
.
.
.
.
(7.1)
(7.2)
Donde r = radio usado para la interface cubierta-a-boquilla (pulgadas), y T = grosor de la cubierta (pulgadas).
98
Tabla 7.2
Hoja de computo para esfuerzos locales en cubiertas (cuerpos cilíndricos) Referencia 1.
99
Tabla 7.3
Hoja de calculo para esfuerzos locales en cubiertas(cuerpos) esféricos (accesorio hueco) Referencia 1
100
Ejemplos problema
1.
Calcule los esfuerzos locales para el recipiente cilíndrico dado como sigue (referencia 1):
= 72 pulg
Radio del recipiente =
Grosor del recipiente = T = 0.4375 pulg
Radio del accesorio = = 3.125 pulg
Los parámetros geométricos son:
v=
=
β =0.875
= 164
.
= 0.875
.
= 0.043
Los factores de concentración de presión son para la carga de membrana
Las cargas aplicadas son: Carga radial P = - 97.8 lb
= - 768 pulg - lb
Momento circular
Momento longitudinal = - 10 152
= 31 368
Momento torsional
Carga de corte = - 4
Carga de corte = - 451
Las constantes no dimensionales leídas de las graficas del WRC 107 son:
WRC 107 Numero de grafica
3C
Constante
Ø
Valor
30
1C
Ø
0.15
3A
Ø
4.1
Ø
0.095
Ø
16
Ø
0.048
= 1. Para la carga de flexion
=1.
/
/
1A
/
3B
/
1B ó 1B-1
/
4C
30
/
2C
0.095
4A
5.6
/
2A
0.055
/
4B
4.2
/
2B ó 2B-1
0.075
/
101
Ejemplo problema
2.
Calcular los esfuerzos locales para el recipiente esférico a continuación:
Radio del recipiente = = 167.43 pulg
Grosor del recipiente = T = 1.125 pulg
Grosor de boquilla =0.5
Radio medio de boquilla = 11.75
Radio exterior boquilla = 12
Las cargas aplicadas son :
Carga radial = p = 1 977 lb
Carga de corte = = 97
Carga de corte = = - 36
= - 158 808 pulg-lb
Momento de vuelco =
= - 47 976 pulg-lb
Momento de vuelco =
= - 10 344 pulg-lb
Momento de torsion =
=2
y
=2
Los factores de concentración son:
Los parámetros geométricos son:
v=
=
.
.
= 23.5
ρ= =
.
.
= 2.25
U=
=
√
.
.
= 0.8746
Las constantes no dimensionales de las graficas WRC 107 son las siguientes :
SP 1 a SP 10
0.0078
SM 1 a SM 10
0.04
0.03
0.09
SP 1 a SP 10
0.055
0.083
0.025
0.33
0.189
SM 1 a SM 10
0.025
0.119
0.068
En un esfuerzo para extender los resultados del WRC 107 para valores mayores de D/T y menores de d/D y para incluir el efecto del
grosor de la boquilla, se presentan los cálculos usando las soluciones de Flüge-Conrad (referencia 2).
El boletín WRC 297 (referencia 8) amplia la cubierta del boletín 107, y esta basado en la teoría de Steele (referncia 2). El WRC 297
incluye el efecto del grosor de boquilla y datos de flexibilidad de la boquilla. La boquilla y el recipiente son tratados como cuerpos
cilíndricos de pared delgada.
102
7.2
Tasa de resorte rotacional para recipientes cilíndricos
Como una aproximación conservadora, las boquillas de los recipientes son consideradas rigidas en los cálculos de esfuerzo de tubería.
Sin embargo, el recipiente o tambor tienen flexibilidad inherente que puede ser usada ventajosamente para obtener mas bajos y mas
reales momentos externos.
Fuera de las tres fuerzas primarias y los tres momentos primarios que puede ser aplicados al cuerpo de la cubierta y a la boquilla,
solo la fuerza radial y dos momentos son considerados significantes en las causas de la deflexión del cuerpo. Las rotaciones de los
extremos elásticos son generalmente mas importantes que las traslaciones. Por eso las traslaciones elásticas de las boquillas y la
flexibilidad radial son ignoradas.
Las tasa de muelleo en plano y fuera de plano son importantes; En un recipiente cilíndrico, la tas de muelleo en plano corresponde al
momento longitudinal, y la tasa de muelleo fuera de plano corresponde al momento circunferencial. Como se muestra en la figura
7.1, por la aplicación del momento flexor longitudinal, el plano formado por las líneas de centro del cuerpo y la boquilla permanecen
en plano. El momento circunferencial será el momento fuera de plano a causa de que este momento llevará a la boquilla duera
del plano original.
Figura 7.1
Arreglo de recipiente y boquilla.
Cargas de tubería
El punto de vista que usan los resultados de las constantes de resorteo rotacional en valores no-conservadores para momentos
flexores, debieran ser investigados. Es conocido que las cargas primarias en tubería( peso, presión) y su efecto permanecen en igual
magnitud, mientras que las cargas secundarias (térmica) y su efecto aflojan en si mismas cuando la resistencia se reduce. Un ejemplo
es el que sucede bajo carga térmica, los momentos flexores actúan sobre la boquilla y caen cuando se permite la rotación. Todos los
sistemas estructurales tienen flexibilidad inherente, que es expresada como tasas de resorteo rotacional para recipientes y conexiones
de boquillas; estas tasas de resorteo debieran ser usadas para boquillas de bombas, turbinas y compresores.
La ecuacion 7.3 puede ser usada para calcular rigidez rotacional en la boquilla de conexión. La ecuacion 7.4 expresa la formula para
calcular el factor de flexibilidad K; los valores para la constante C es 0.09 para flexion en plano y C es 0.27 para la flexion fuera de
plano (referencia 3)
=
donde
(7.3)
= constante de resorteo pulg-lb/grado
M = momento flexor, pulg-lb
103
θ = angulo de rotación, radianes
E = modulo de elasticidad en condiciones frias, psi
I = momento de inercia del area de la boquilla,
DN = Diametro de la boquilla, pulg
K = factor de flexibilidad.
El factor de flexibilidad K:
K=C
(7.4)
Donde C = 0.09 constante para flexion en plano.
C = 0.27 para flexion fuera de plano.
D = diámetro del recipiente,pulg.
T = grosor de pared del recipiente, pulg.
DN = diámetro de la boquilla, pulg.
TN = grosor de pared de la boquilla, pulg.
Estas tasas de muelleo no debieran ser usadas si la boquilla o el diámetro del refuerzo es mayor que un tercio del diámetro del
recipiente o cabezal.
Ejemplo problema
Los siguientes cuatro casos son considerados para calcular la tasa de muelleo:
1.
La boquilla en la figura 7.2 será tratada como rígida.
Figura 7.2
2.
3.
4.
Arreglo de tubería para comparación de tasa de muelleo.
Usando rigidez rotacional para un recipiente de 48 pulgadas de diámetro.
Usando rigidez rotacional para un recipiente de 60 pulgadas de diámetro.
Usando rigidez rotacional para un recipiente de 96 pulgadas de diámetro.
El calculo de la constante de muelleo para el recipiente de 48 pulgadas, 1 pulgada de grosor y 12.7 pulgadas de diámetro exterior , y
0.375 pulgadas de grosor de boquilla, es como sigue:
104
K=C
.
= 0.09
.
.
= 0.27
= 2.98
.
= 8.94
La constante de muelleo es:
=
.
=
.
La constante de muelleo en plano con
como 2.98 = 358 x 10 pulg-lb/grado. La constante de muelleo fuera de plano con
Como 8.94 = 119 x 10 pulg-lb/grado.
La tabla 7.4 da valores calculados de constantes de muelleo para los casos considerados.
Diámetro recipiente (pulg)
Tasa muelleo longitudinal (en plano)
(Pulg-lb / grado)
48
60
96
358
320
253
Tabla 7.4
Tasa muelleo circunferencial (fuera plano)
(Pulg-lb / grado)
10
10
10
119
107
844
10
10
10
Valores calculados para constantes de muelleo
Los análisis de esfuerzos de tubería que fueron hechos para los cuatro casos ( tres diferentes diámetros de recipiente ) y los
momentos y fuerzas en la boquilla están dados en la tabla 7.5. Como puede verse fácilmente, los valores del momento flexor en los
ejes “x-“ y “y-“ han caído cuando la flexibilidad de la boquilla del recipiente esta incluida. También muestra al de 48” de diámetro
comparado cuando la flexibilidad no esta incluida.
Fuerza (lb)
Momento (pie-lb)
CASO
Sin flexibilidad
- 481
5 066
-388
25 457
2 248
-583
48”
-476
1 866
-466
9 994
2 004
-485
60”
-475
1 727
-469
9 321
1 989
-476
96”
-474
1 450
-476
7 980
1 918
-451
Tabla 7.5
Fuerzas y momentos en la boquilla del recipiente
El problema ejemplo dado en la figura 7.2 fue seleccionado para comparar los valores de tasa de muelleo calculados aquí, con
resultados ya publicados usando una aproximación ligeramente diferente,
En el recipiente cilíndrico:
Cuerpo 132 pulg, grosor 0.625 pulg.
Tubo 35 pulg, grosor 0.5 pulg
E = 27.9 x 10 psi
I = 8 785
105
El factor de flexibilidad fuera de plano es:
La tasa de muelleo fuera de plano es:
.
= 0.27
=
=
.
.
.
.
= 180.8
= 776 569 pulg-lb/grado.
La tabla 7.6 nos da valores calculados de tasa de muelleo. Los valores dados son para un recipiente de 132” Diam ext x 0.625” grosor,
con un tubo de 36” Diam ext x 0.5” grosor. Como se puede ver os valores están próximos, conociendo los valores usados para rigidez
para un sistema 10 pulg-lb/grado.
Tabla 7.6
Comparación de tasas de muelleo calculadas
Constante de Muelleo
Fuente
Stevens,P.G. (referencia 5)
Simplex (referencia 6)
Bijlaard,P.P. (referencia 7)
Ecuacion 7.3
(pulg-lb/grado)(fuera plano)
727 200
659 712
588 252
776 569
Los valores de tasa de muelleo cuando son usados dan momentos de flexion reducidos, asi evitan mas tubería, placas de refuerzo, o la
consideración de arreglos alternos de tubería.
El rango de esfuerzo en el cuerpo del recipiente, el cual viene bajo el código de recipientes a presión es de importancia pero no se
discute aquí. Las ecuaciones dadas aquí son asistencia cuando los momentos de flexion son ligeramente mas altos que los permitidos,
y estos valores ligeramente mas altos pueden reducirse en el análisis por el uso de constantes de tasa de muelleo.
Referencias
1.
2.
3.
4.
5.
6.
7.
8.
Wicman,K.R. “Local Stresses in spherical and Cylindrical Shells due to external loadings”, Welding Research Council Bulletin
107 (revised March 1979)
Steel,C.R. “Stress Analysis of Nozzles in Cylindrical Vessels with External Load”, Journal Pressure Vessel Technology, Vol 105
(august 1983)
Kannappan S. “Effect of Inclusion of Rotacional Spring Rate of Vessel Nozzles in Pipe Stress Calculations”, Society of Piping
Engineers Conference. Houston in October 1982
Oakridge National Laboratory (ORNL) Phase report 115.3
Stevens,P.G. et al “Vessel Nozzle and Piping Flexibility Analysis” Journal of Engineering for Industry”,May 1962, p 225.
Simplex Computer Program User´s Manual. Peng Engineering.
Bijlaard P.P. “ Stresses from Radial Loads and External Moments in Cylindrical Vessel” The Welding Journal, Vol 34 (1955)
Mershon,J.J. WRC bulletin 297, August 1984, Supplement to WRC Bulletin 107
106
CAPITULO OCHO
Tubería conectada a equipo rotatorio.
Las cargas externas impuestas por la tubería sobre las boquillas del equipo rotatorio debieran ser menos que las cargas permisibles.
Ejemplos de equipos rotatorios son: bombas centrifugas, turbinas de vapor y compresores centrífugos.
Si cargas excesivas son impuestas, el desalineamiento puede ocasionar que afecte la operación mecánica y podía ocasionar vibración
objetable. Un alineamiento cerrado debe ser mantenido entre las partes rotatorias y estacionarias ; la provisión para la expansión de
la carcasa y el mantenimiento de los claros cerrados, requiere que las fuerzas y momentos debidos a la tubería sean limitados.
En lugar de duplicar lo que se obtiene en otras fuentes, los ejemplos se dan aquí con referencia a diferentes estándares.
8.1
Tubería conectada a turbinas de vapor
Los estándares NEMA SM 23 (referencia 1) remarca guías para calcular cargas permisibles.
Este estándar tiene dos partes:
1.
Permisibles locales en cada boquilla.
2.
Permisibles combinadas para comparación de cargas transferidas a centro de línea de boquilla de descarga.
El método para transferir fuerzas y momentos esta dado en la ecuación 8.1 . La siguiente ecuación es dada para dos boquillas, pero la
misma ecuación puede ser extendida más allá (referencia 2):
∑
∑
∑
∑
∑
∑
= ( entrada ) + ( descarga )
= ( entrada ) + ( descarga )
= ( entrada ) + ( descarga )
=
( entrada ) +
( descarga ) =
( entrada ) +
( descarga ) =
( entrada ) +
( descarga ) -
( entrada ) (
( entrada ) (
( entrada ) (
+
+
( descarga ) ( )
( descarga ) ( )
( descarga ) ( )
Ejemplo problema
Revise, si la carga real dada en la boquilla de entrada y salida de la turbina de vapor bipartida verticalmente de una sola etapa esta
bajo la norma NEMA. El diámetro de entrada es 3” Ø y el diámetro de descarga es 8”Ø. El sistema NEMA de coordenadas ( El eje X
paralelo a la flecha de la turbina ) es dado en la figura 8.1. Dos vistas de la turbina están dadas en las figuras 8.2 y 8.3 (referencia 3).
La orientación de los ejes X, Y y Z y las distancias , y para el ejemplo problema están mostrados en las figuras 8.2 y 8.3.
y
las distancias son medidas desde la línea de centro de la válvula de descarga. El signo menos (-) mostrado con las distancias
corresponden con las sumatorias de los momentos de la ecuación 8.1. El signo para estas distancias depende sobre la localización
de la boquilla de entrada con respecto a la boquilla de salida en el sistema NEMA. Las fuerzas locales y los momentos en las boquillas
de entrada y descarga obtenidas del análisis de esfuerzos del tubo, se alistan en la tabla 8.1
107
Figura 8.1
Figura 8.2
Figura 8.3
Sistema de coordenadas usado en el estándar NEMA
Turbina de vapor bipartida verticalmente de etapa simple.
Las distancias X , Y y Z usadas en el problema ejemplo para la ecuación 8.1
108
Tabla 8.1
Fuerzas y momentos del Analisis
Fuerzas y momentos
( libras )
Entrada
Descarga
- 30
- 55
204
213
120
- 67
127
185
( pie-libras )
- 155
1 095
170
1 119
44
- 425
- 722
839
Los componentes de las fuerzas y momentos resultantes después de su transferencia a la salida pueden ser obtenidos por el uso de la
ecuación 8.1
∑
∑
∑
∑
∑
∑
= 30 + 155 = - 185 lb
= 55 + 1 095 = 1 040 lb
= 204 + 170 = 374 lb
= 120 + 44 - 55 2.3 + 204 2.25 = 494. 85 pie - libra
= 67+ 425 + 30 2.33 - 204 2.08 = 2.22 pie - libra
= 124 - 722 - 30 2.25 + 55 2.08 = - 416 pie - libra
La fuerza y momento resultantes combinados después de ser transferidos a la descarga son como sigue:
La fuerza combinada resultante a la descarga =
185
El momento resultante combinada a la descarga =
494.85
1 040
= 1 121 lb
374
2.22
416
= 647 pie - lb
Fuerzas y momentos locales permisibles
La regla 1 de NEMA se aplica para calcular la fuerza local resultante permisible:
para la descarga
= 166.6 D -
= 166.6 (8) -
= 1 053 lb
(regla 1)
Una grafica (figura 8.4) puede ser usada para determinar la fuerza resultante permisible. El calculo se muestra con líneas punteadas.
Para la entrada,
= 166.6 D -
= 166.6 (3) -
= 438 lb
109
Figura 8.4
Relación Fuerza - Momento usando el estándar SM 23 NEMA
Los componentes permisibles de las fuerzas y momentos resultantes después de ser transferidos a la descarga, usando la regla 2b del
NEMA,
Diámetro equivalente =
=
Esto esta debajo de el limite de 9” para el diámetro , dada en el código NEMA; por esto
= 50 ( 8.544) = 427 lb
= 125 (8.544) = 1 068 lb
= 100 (8.544) = 854.4 lb
=√3
8 =8.544
= diámetro equivalente = 8.544.
= 250 (8.544) = 2 136 pie-lb
= 125 (8.544) = 1 068 pie-lb ( regla 2b )
= 125 (8.544) = 1 068 pie-lb
La fuerza y momento resultante combinado permisible en la descarga usando la ecuación 2b NEMA es,
=
=
.
= 744.5 lb
( Regla 2a )
Cuando la carga real es mas alta que la permisible, se debe entrevistar a los vendedores de la turbia para que den las mas altas cargas
aprobadas. Según la experiencia de los ingenieros de esfuerzos los valores permisibles son conservadores; sería muy útil ,que NEMA
publique las bases de criterio de las ecuaciones dadas.
110
Tabla 8.2
Comparación de fuerzas y momentos reales y permisibles
Boquilla
Entrada
Descarga
Componentes
Real
= 213 lb
= 1 119 lb
= - 185 lb
= 1 040 lb
= 374 lb
= 495
=2
= - 416
= 1 121 lb
Resultante combinada
8.2
Permisible
= 438 lb
= 1 054 lb
= 424 lb
= 1 068 lb
= 854 lb
= 2 136
= 1 068
= 1 068
= 745 lb
Observaciones
OK
Excede
OK
OK
OK
OK
OK
OK
Excede
Tubería conectada a compresores centrífugos
El estándar 617 de API se refiere al NEMA SM 23 como la base para las cargas permisibles; las ediciones de 1979 y 1973 tienen
ligeramente diferentes palabras en su texto.
El API 617, 1979, Sección 2.5.1, pagina 7, “ Los compresores debieran ser diseñados para resistir fuerzas y momentos externos al
menos o igual a 1.85 veces los valores calculados de acuerdo al NEMA SM 23”
El API 617, 1973, Sección 2.4.1, pagina 5,”Los compresores debieran ser diseñados para resistir fuerzas y momentos al menos igual a
los calculados del NEMA 23; estas constantes de calculo de la formula serán incrementadas por un factor de 1.85”
El ejemplo presentado anteriormente para turbinas de vapor, puede ser usado por la misma vía para compresores centrífugos,
excepto por el factor 1.85. Las referencias 4 a 6 se aplican para compresores centrífugos. Consideración especial para vibración
dinámica se necesita en el caso de compresores reciprocantes, los cuales están fuera de esta discusión.
8.3
Tubería conectada a bombas centrifugas
El estándar API 610 (referencia 7) nos da ecuaciones para calcular las fuerzas y momentos permisibles en el caso de bombas
centrifugas para servicio general en refinerías. El criterio se aplica a bombas con boquillas de descarga de 4”Ø o mas pequeñas ( las
boquillas de succión pueden ser mas grandes), y situaciones donde la bomba esta construida de acero ó aleación de acero. El modulo
de elasticidad para el material de tubería a la temperatura de operación (conocido como modulo caliente), puede ser usado para
calcular cargas reales. Usando el modulo caliente resultará en cargas mas bajas, a causa de que la tueria es mas flexible a altas
temperaturas.
Figura 8.5 a
Sistema de coordenadas del estándar API 610 para bombas.
111
Figura 8.5 b
Sistema de coordenadas para momentos y fuerzas en la tablas API 2.1A (2.1B) para bombas horizontales con
boquillas de entrada y descarga en el lado.
Figura 8.5 c
Sistema de coordenadas para momentos y fuerzas en la tablas API 2.1A (2.1B) para bombas horizontales con
boquillas de entrada al frente y descarga hacia arriba.
Las figuras 8.5 a, b y c nos dan el sistema de coordenadas usado por el API 610 para bombas; la flecha de la bomba es paralela al eje
X, y el eje Z esta a lo largo del centro de línea del pedestal. Para bombas de diámetro mas grande, los valores permisibles pueden ser
obtenidos de los proveedores, o determinados por medios experimentales (referencias 8 y 9).
Anexo a continuación las tablas a las que se refieren las figuras 8.5 b , c. Que son las mas al dia que pude obtener.
112
113
La fuerza permisible para cada boquilla es:
≤ 1.3 W ≤ 160 lb / diámetro nominal
≤ 1.0 W ≤ 130 lb / diámetro nominal
≤ 200 lb / diámetro nominal ≤ 1.2 W
≤ 100 lb / diámetro nominal ≤ 0.5 W
donde W = peso de la bomba.
La fuerza de corte resultante es:
=
≤ 2 000 lb
∑
= 3.4 W pie-libra
∑
= 2.0 W pie-libra
∑
= 1.5 W pie-libra
Donde el máximo valor para W es 1 000 libras.
Los momentos permisibles son:
Las fuerzas y momentos reales de ambas boquillas la de succión y la de descarga serán transferidas a la intersección de los ejes X, Y ,
y Z , para obtener la sumatoria de momentos en cada dirección para comparación con las permisibles. El menor de los valores
obtenidos del peso considerado y el diámetro debieran ser usados como los permisibles.
8.4
Método de deformación de tubería.
El método de deformación de tubería es un caso extremo en el cual el componente esta dado con la suficiente fuerza para deformar
completamente la tubería conectada en la flexión de la boquilla. Elñ sistema de coordenadas y ecuaciones dadas en la referencia 10 se
presentan en la figura 8.6
Figura 8.6
Sistema de coordenadas de boquilla de tubería
Las fuerzas y momentos para los cuales el equipo necesita ser diseñado son como sigue:
=
=
fuerza axial ( a lo largo del eje de la boquilla )
114
=
=
= 1.3
Momento de flexión
=
Momento de torsión
Ecuaciones que son ligeramente diferentes de estas se usan también en la industria (referencia 11):
=
= 0.01
Area de metal de tubería
El momento flexor acerca de las direcciones ortogonales ( otras que la torsión ) es:
=
= 0.0707
El momento de torsión esta expresado por:
=
= 0.1
El sistema de coordenadas para las ecuaciones de arriba es la misma como en la figura 8.6
= esfuerzo de deformación (cedencia) del material del tubo (máximo de 36 000 psi)
modulo de sección del tubo,
Método de fracción de seis componentes para revisión de cargas en boquillas.
El método de fracción de seis componentes, requiere que la suma de las relaciones de las cargas reales entre las cargas permisibles
del vendedor sean iguales o menores que la unidad.
+
+
+
≤1
Referencias
1.
2.
3.
4.
5.
6.
National Electrical Manufacturers Association. Publication No. SM 23, 1979 Sec SM 23, 8.06, “Steam Turbine for Mechanical
Drive Service “
General Electric Company. “Design Recommendations for steam Piping Systems”, manual number GEK-27,060
Kannappan, S et al. “How to Determine Allowable Steam Turbine Loads”. Hydrocarbon Processing, Vol 53, No 8 ( August
1974), p 75
American Petroleum Institute API 617, 4a edición (november 1979), sec 2.5.1, “Centrifugal Compressors for Refining
Service”
American Petroleum Institute API 617, 3a ed. (October 1973) sec 2.4.1, “Cenrifugal Compressors for Refining Service”
Kannappan,S. “ Determining Centrifugal Compressor Piping loads” Hydrocarbon Processing ( February 1982) p 91
115
7.
8.
9.
10.
Amercan Petroleum Institute API 610. “ Centrifugal Pumps for General Srvice” Sec 14
Simmon C. A. “ Allowable Pump Piping Loads “ Hydrocarbon Processing , p 98
Doolin J. H. “ Install Pumps for Minimum Stress” Hydrocarbon Processing”,p 96
Meyer R.A. “Survey of Nozzle Piping Reaction Criteria for.. .. Structural Design of Nuclear Plant Facilities,Vol II,p 283
116
CAPITULO NUEVE
Temas especiales.
Los temas que no caen dentro de las categorías de los otros capítulos, se agrupan y discuten a continuación:
Válvulas.
Empujes de válvulas de alivio de presión.
Tuberías de aleación de Aluminio, Níquel, y cobre.
Tuberías subterráneas y de plástico.
Diseño de presión externa - Tuberia enchaquetada.
Unidades métricas.
Temperatura elevada - Efectos de deslizamiento.
Recubrimiento refractario.
9.1
Válvulas
Las válvulas son usadas en un sistema de tubería para alcanzar lo siguiente:
1.
2.
3.
4.
5.
Para detener o comenzar el flujo de fluidos; Los ejemplos son: compuerta, pistón (macho), bola o mariposa.
Para regular flujo; los ejemplos son: globo, Angulo, aguja, y mariposa.
Para prevenir el retorno del flujo; los ejemplos son: retención de disco y retención de columpio.
Para regular presión; un ejemplo es el regulador de presión.
Para relevar presión; Los ejemplos son: las válvulas de seguridad de resorte o válvulas pop, las válvulas de alivio .
Hay numerosos manufactureros haciendo válvulas para diferentes usos; la referencia 1 enlista alguna de la información de los
manufactureros acerca de las válvulas para aplicación en tuberías.
Válvulas de compuerta
Las válvulas de compuerta conectan tres componentes mayores: cuerpo, bonete, y mecanismo (referencia1). El cuerpo esta
generalmente conectado a la tubería por medio de bridas, rosca o conexiones soldadas. El bonete contiene las partes en movimiento,
se une al cuerpo generalmente con tornillos, para permitir limpieza y mantenimiento. El mecanismo incluye el vástago, la compuerta,
la guillotina o disco y los anillos del asiento.
117
Materiales del cuerpo de la válvula
Los cuerpos de las válvulas están hechos de latón o bronce principalmente en los tamaños pequeños y para presiones
y temperaturas moderadas. El fierro fundido se usa en la mayoría de los servicios; el acero forjado se usa para
servicios severos o altas presiones y temperaturas.
Materiales del mecanismo de la válvula
Los materiales del mecanismo de la válvula incluyen el anillo del asiento, disco y vástago; los materiales comunes del mecanismo son
monel, bronce, estelita, y acero inoxidable. Entre los principales factores que influyen el desempeño de los materiales del
mecanismo: (1) propiedades tensiles, estabilidad química, y resistencia química a la temperatura de operación; (2) dureza y
rugosidad; (3) un coeficiente de expansión que corresponda cerradamente a ese del cuerpo de la válvula: y (4) diferencia en
propiedades del asiento y el disco para impedir se traben.
El tipo de válvula que se usa para un servicio dado se presenta en la especificación de tubería ( figura 1.3). En general, los análisis
preliminares de esfuerzo se sacan con el peso aproximado. El peso real obtenido del manufacturero (referencia 1) debiera ser usado
en el análisis de esfuerzo final en los sistemas críticos. En tuberías nucleares, las válvulas son agrupadas adicionalmente como (1)
válvulas activas y (2) válvulas no activas que están basadas sobre el requerimiento de desempeño después de un evento de terremoto
(capitulo 10). El modelado de válvulas en análisis computarizado esta descrito en el capitulo 10( fig 10.19). Las válvulas requieren
soporte rigido próximo al centro de gravedad. Es aconsejable evitar soportes sobre los operadores de la válvulas. En general, la
máxima aceleración a que una válvula puede estar sujeta es 3 g . Si la aceleración real excede la permisible, el proveedor de la
válvula se debe contactar.
Válvulas de alivio de presión
Presión de diseño y velocidad para descargas abiertas. Instalación de codos de descarga y tuberías de venteo.
Hay diversos métodos asequibles al diseñador para determinar la presión de diseño y velocidad en el codo de descarga y tubo de
venteo. Es responsabilidad del diseñador asegurarse a si mismo que el método admite resultados conservadores. Un método para
determinar la presión de diseño y velocidades en el codo de descarga y tubo de venteo, para instalación de descarga abierta, se
muestra a continuación y se ilustra en el ejemplo problema.
Primero, calcular la presión de diseño y velocidad en el codo de descarga.
1.
Determine la presión que existe en el codo de descarga de salida (figura 9.1)
=
2.
Determine la velocidad
(9.1)
que existe en el codo de descarga de salida (figura 9.1)
=
(9.2)
118
donde W = tasa de flujo másico real, lbm/seg
= Área del codo de descarga, pulg
Entalpia de estancamiento en la entrada de la válvula de seguridad. BTU / lb
= Constante gravitacional = 32.2 lbm-pie/lbf= Presión, psia (lbf/, pulg , absolutos)
V = pie/seg
Figura 9.1
Válvula de seguridad.
Los valores comunes de a y b se enlistan en la tabla 9.1
Tabla 9.1
Condiciones del vapor
A, BTU / lbm
b
Vapor húmedo, < 90% de calidad
291
11
Vapor saturado, 90% de calidad, 15 psia
≤ 1 000 psia
Vapor sobrecalentado, 90% de calidad, 1 000 psia < ≤ 2 000 psia *
*
Este método puede ser usado como una aproximación. Para presiones > 2 000 psi, se debiera usar un método alternativo de
verificación.
119
Fuerzas de reacción con el sistema de descarga abierto
Codo de descarga
La fuerza de reacción F debida al flujo en estado continuo, siguiendo la abertura de la valvula de seguridad, incluyendo ambos
efectos momento y presión. La fuerza de reacción aplicada se muestra en la figura 9.1, y puede ser calculada por la siguiente
ecuación:
=
Donde
+(
-
(9.3)
= fuerza de reacción, lbf en el punto 1
W = Tasa de flujo másico, ( capacidad de alivio estampada en la válvula x 1.11 ), lbm /seg
= constante gravitacional = 32.2 lbm-pie/lbf= velocidad de salida en el punto 1, pie/seg
= Presión estática en el punto 1, psia
= área de flujo de salida en el punto 1, pulg
Para asegurar la consideración de los efectos de una carga F súbitamente aplicada, un factor de carga dinámica DLF debiera ser
aplicado ( figura 9.2 ).
Figura 9.2
Factores de carga dinámica para sistema abierto de descarga
Los métodos para calcular las velocidades y presiones en los puntos de salida del codo de descarga son los mismos que esos
discutidos en las ecuaciones 9.1 y 9.2.
120
9.2
Análisis para las fuerzas de reacción debidas a la válvula de descarga.
Sistemas de descarga abierta
Los momentos debidos a las fuerzas de reacción de la válvula pueden ser calculados por la simple multiplicación de la fuerza,
calculada como se describe en la ecuación 9.3, por (veces) la distancia desde el punto en que la tubería esta siendo analizada,
por(veces) un apropiado factor dinámico. En ningún caso será tomado el momento de reacción en la conexión del ramal debajo de la
válvula, en menos que el producto dado en la ecuación 9.4
Momento ≥ ( DLF ) ( ) ( D )
(9.4)
= Fuerza calculada en la ecuación 9.3
D = Diámetro nominal del tubo de entrada
DLF = factor de carga dinámico ( figura 9.2 )
Los efectos de la fuerza de reacción y el momento resultante sobre el cabezal, soportes y boquillas de cada una de las válvulas o
combinación de válvulas soplando, debiera ser considerado.
Donde
Amplificación de fuerzas de reacción
En un sistema de tuberías actuado sobre cargas que varían con el tiempo, las fuerzas y momentos son generalmente mayores, que
esos producidos bajo aplicación estática de la carga. Esta amplificación es frecuentemente expresada como el factor de carga
dinámica DLF, y es definida como la relación máxima de la deflexión dinámica a cualquier tiempo entre la deflexión que sería
resultado de la aplicación estatica de la carga. Para estructuras teniendo esencialmente un grado de libertad y una aplicación de
carga simple, el valor de DLF oscilará entre uno y dos dependiendo de la historia con respecto al tiempo de la carga aplicada, y la
frecuencia natural de la estructura. Si la tubería que corre esta rígidamente soportada, la instalación de la valvula de seguridad
puede ser idealizada como un sistema de un grado de libertad, y la historia-tiempo de las cargas aplicadas puede frecuentemente ser
asumida a ser una función simple de enlace, entre la no-carga y la condición de estado continuo; en este caso el DLF puede ser
determinado de la siguiente manera.
1.
Calcular el periodo T de la instalación de la válvula de seguridad usando la siguiente ecuacion y figura 9.2:
T = 0.1846
(9.5)
Donde T = Periodo de instalación de la válvula de seguridad, seg
W= peso de la valvula de seguridad, tubería de instalación, bridas, aditamentos, etc, lb
h = distancia desde donde corre la tubería al centro de línea de la tubería de descarga, pulg
E = Modulo de Young de la tubería de entrada, lb/pulg , a la temperatura de diseño
I = Momento de inercia de la tubería de entrada, pulg
121
2.
3.
Calcular la relación del tiempo de apertura de la válvula para el periodo de instalación ( / ) donde es el tiempo que
la válvula de seguridad toma de la posición completamente cerrada a completamente (seg), y T esta determinado en el inciso
1 anterior.
Entrar en la figura 9.2 con la relación de tiempo de apertura entre el periodo de instalación, y lea el DLF de las ordenadas; El
DLF nunca debiera ser tomado menos de 1.1.
Si el DLF conservador menor es usado, El DLF debiera será determinado por calculo o prueba.
Ejemplo de calculo de fuerzas de reacción con sistemas de descarga abierto.
Calcular la fuerza de reacción con lo que se ve en la figura 9.3
Figura 9.3
Problema ejemplo para sistema de descarga abierto
Temperatura de operación = 700°F
Presion de operación = 200 psig
= 1 374 BTU/lbm de la tabla de vapor
a = 823 BTU/lbm
b = 4.33 ( de la tabla 9.1 )
W=
= 55.6 lbm/seg
= 50 pulg
J = 778.16 pie-lb/lbf-seg
Se asume que el factor de carga dinámica es 2.
Por lo tanto
=
=
=
Por lo tanto
=
=
+(
-
.
.
.
.
.
.
.
=
.
.
.
.
= 50 psig
= 1 899 pie/seg
x 1 899 + (50 - 14.7 50= 3 404.5
= F (DLF) = 3 404,2 x 2 = 6 809 lb
122
9.3
Tubería de aluminio
Diferentes aleaciones de tubería de aluminio tienen similar resistencia deseable a la corrosión pero varia en las propiedades
mecánicas. La mayoría de aleaciones de aluminio comúnmente usadas para sistemas de tubería son: aleación 160, aleación 3003,
aleación 5052, aleación 6061 y aleación 6063. De estos, la aleación ASTM B241-6063-T6 es la que mas ampliamente se usa, a causa de
que tiene buenas propiedades mecánicas en un costo razonable.
El aluminio ha hallado varios usos en las aplicaciones criogénicas y de baja temperatura. Cuando la temperatura del aluminio
decrece, muestra incremento en los valores esfuerzo tensil y de cedencia, con igual ó incrementada ductivilidad ó resistencia al
impacto. Las aleaciones especificas mas frecuentemente usadas en aplicaciones de temperatura fría son la alloy 3003 y la alloy 5052.
Las aleaciones de aluminio pueden ser soldadas: El método arco-gas inerte-tugsteno usando gas argón, es el procedimiento
recomendado. Referencias adicionales acerca de material y técnicas de instalación, accesorios, etc, pueden ser obtenidos de
compañías manufactureras de metal como ALCOA y Reynolds.
Tabla 9.2
Propiedades
Propiedades físicas de varias aleaciones de aluminio
Aleacion
3003
Esfuerzo tensil, psi
Esfuerzo de cedencia, psi
Modulo de elasticidad, psi x 10
Conductividad térmica, BTU/hr/ /°F/pulg
Coeficiente promedio de expansión térmica, pulg/°F/pulg x 10
- 58 a 68°F
68 a 212°F
68 a 392°F
68 a 572°F
12 x 10
12.9 x 10
13.5 x 10
13.9 x 10
5052
12 x 10
6061
6063
2.1 x 10
13 x 10
13.5 x 10
14.1 x 10
12.1 x 10
13 x 10
13.6 x 10
14.2 x 10
La tabla 9.2 muestra las propiedades físicas de varias aleaciones de aluminio (referencia 4). Como se puede ver, las unidades para la
expansión térmica promedio están dadas en pulg/°F/pulg; vea el capitulo 1 (ecuacion 1.1) para la conversión a pulg/pie lineal de
tubería. La expansión térmica para aluminio es alta y provisión adecuada debe ser hecha para compensar la alta cantidad de
expansión. La presión de operación de una tubería de aluminio se calcula de la misma manera de la tubería ferrosa, usando la
ecuación 2.4 con y = 0.4 y corrosión permisible de 0.
El aluminio esta sujeto a corrosión galvanica en la presencia de un electrolito. Cuando esta en la presencia de acero al carbón, cobre,
bronce, níquel, y plomo, el aluminio se corroerá. Por eso, los colgadores de tubería de acero al carbón debieran ser evitados; sin
embargo, las series 300 de acero inoxidable y Zinc son usualmente compatibles con aluminio. Por esto los colgadores de acero
galvanizado (cubierto de Zinc), colgadores de aluminio o colgadores recubiertos pueden ser usados. La tabla 9.3 da espaciado de
soportes (referencia 4) para tubería de aleación 6063.
La tabla esta basada en que la tubería no esta aislada, operando a una temperatura máxima dwe 400°F, y transportando un liquido de
gravedad especifica 1.35 ( condición conservadora ). Si la línea esta aislada, reducir el claro 30%. Ninguna tolerancia ha sido hecha
para cargas concentradas tales como válvulas. Las ecuaciones 3.1 y 3.2 pueden ser usadas para calcular el claro.
123
Tabla 9.3
Espaciado de soportes para tubería de aleación de aluminio 6063
Tamaño nominal
de tubería
(pulgadas)
1/2
3/4
1
1½
2
3
4
6
8
10
12
Numero de cedula de tubería
10 S
Espaciado de soportes ( pies )
5.5
6.0
7.0
7.5
8.0
8.5
9.0
10.0
11.0
11.5
13.0
5S
5.0
5.5
6.0
6.5
6.5
7.5
8.0
9.0
9.5
10.0
10.5
9.4
40 S
6.0
6.5
7.5
8.5
9.0
10.0
11.5
13.0
14.0
15.0
15.5
Tubería de aleación de cobre
Muchas aplicaciones de la tubería de cobre han sido encontradas en la industria de la alimentación. La tabla 9.4 muestra las
propiedades físicas. El coeficiente de expansión térmica de la tubería de cobre es alto; por eso, espiras ó juntas de expansión deben
ser proporcionadas para absorber la expansión. La tubería de cobre puede ser unida por: rosca, soldadura de plomo ó soldadura, y
bridas, puede ser instalada por cualquiera de estos métodos. La tabla 9.5 a da dimensiones de la tubería de cobre (roscado
apropiado), diámetro exterior, grosor de pared, y presiones máximas permisibles a una temperatura de operación de 300°F para
cedula regular. Una tubería de cobre no debiera ser forzada dentro del lugar durante la instalación; forzando la tubería dentro del
lugar y manteniéndola bajo esfuerzo puede causar falla. La tabla 9.5 b da espaciado de soportes para tubería de cobre. El espaciado
esta basado (referencia 4) en una línea no-aislada, operando a una temperatura máxima de 300°F y conduciendo un fluido con
gravedad especifica 1.35. Si las líneas están aisladas, el espaciado debiera ser reducido por un 30%. Ninguna tolerancia ha sido hecha
para cargas concentradas como válvulas. En orden de prevenir corrosión galvánica, colgadores de cobre o compensados no debieran
ser usados en tubería de cobre. La tabla 9.6 muestra esfuerzos permisibles para aleaciones de níquel, cobre y aluminio para los
códigos B3.1., B31.3 y sección III.
Tabla
Propiedades físicas de aleaciones de cobre
Esfuerzo de tensión
Conductividad térmica a 68°F
Coeficiente promedio de expansión térmica lineal 77 - 572°F
Modulo de elasticidad en tensión
54 000 psi
2 364 BTU/hr/ /°F/pulg
9.8 x 10 pulg/°F/pulg
17 x 10 psi
124
Tabla 9.5 a
Tamaño
Tubería nominal
pulgadas
1/8”
1/4”
3/8”
1/2”
3/4”
1”
1 ¼”
1 ½”
2”
2 ½”
3”
3 ½”
4”
5”
6”
8”
10”
12”
Dimensiones de tubería de cobre estándar ( apropiada para roscada)
y presiones de operación máximas permisibles.
Diámetro exterior
Cedula regular
0.405
0.540
0.675
0.840
1.050
1.315
1.660
1.900
2.375
2.875
3.500
4.000
4.500
5.562
6.625
8.625
10.750
12.750
Tabla 9.5 b
Diámetro interior
Grosor pared
0.281
0.376
0.495
0.626
0.822
1.063
1.368
1.0-600
2.063
2.501
3.062
3.500
4.000
5.062
6.125
8.001
10.020
12.000
0.062
0.082
0.090
0.107
0.114
0.126
0.146
0.150
0.156
0.187
0.219
0.250
0.250
0.250
0.250
0.312
0.365
0.375
Presion permisible a
300°F o menor
220
540
540
550
500
340
430
390
330
270
315
350
310
250
210
220
220
210
Espaciado de soportes para tubería de cobre cedula estándar (referencia 4)
Tamaño Tubería nominal (pulgadas)
1/2”
1”
1 ½”
2”
3”
4”
6”
8”
10”
Espaciado (pies)
6.5
8.0
9.5
10.5
12.5
13.5
15.5
17.0
20.0
125
Material
Tubo aleación
aluminio B241
6061 P No.13
Temper T6
Cobre aleación
B647 sobre
4½” Cu-Ni
90/10
Aleación níquel
B161 alloy 200
P No 41
anillado sob 5”
Código
Temperatura del metal ° F
-325ª 150
100°F
200
250
300
350
400
450
500
550
600
650
700
Esfuerzo
cedencia
(ksi)
12.7
9.5
9.5
12.7
9.5
9.5
12.7
9.5
9.5
12.3
9.1
9.1
10.5
7.9
7.9
7.9
6.3
6.3
5.6
4.5
4.4
-
--
-
-
-
-
35
7.4
7.4
8.7
7.0
7.0
6.9
6.9
8.1
6.8
6.8
6.6
6.6
7.8
6.5
6.5
6.4
6.4
7.5
6.2
6.2
-
6.1
6.1
-
5.9
5.2
-
5.1
4.3
-
-
-
13
8
8
8
8
8
8
8
8
8
8
8
8
8
8
8
8
8
8
8
8
8
8
8
-
12
-
B31.3
B31.1
Secc III
clase CL3
B31.3
B31.1
Secc III
clase 2 y 3
B31.3
B31.1
Tabla 9.6
35
13
Esfuerzos permisibles ( ksi ) para aleaciones no-ferrosas
Un número de metales no ferrosos y sus aleaciones son ampliamente usados por su material de tubería resistente a la corrosión; el
zirconio y Titanio son ejemplos de estos metales. El Incoloy, Hasteloy, e Inconel son aleaciones que tienen propiedades buenas
resistentes a la corrosión; estas aleaciones son marca registrada. Su numero de especificación ASTM y propiedades, están dados en la
tabla 9.7. El ASTM anual de 1977 o 1980, parte 8, da mas información.
Tabla 9.7
Propiedades de resistencia a la corrosión de metales y aleaciones
Metal/aleación
Especificación ASTM
Esfuerzo cedencia (ksi)
Incoloy 800
Incoloy 825
Inconel 600
Zirconio Gr
7002 no-aleado
Titanio gr 1
Hastelloy B2 ,
código ASME
1642
Hastelloy C276
Código ASME
1410
B407
B423
B167
42
35
36
B337
B517
25
51
59.8
Coeficiente expansión
térmica (pulg/pulg/°F)
7.9 x 10
7.8 x 10
7.4 x 10
Modulo E
(psi)
28 x10
28 x10
31 x10
14.4 x10
0.333
6.2 x 10
31.4 x10
0.321
7.1 x 10
29.8 x10
Densidad
)
(lb/
0.290
0.294
0.304
0.234
Gravedad
especifica
8.01
8.14
8.43
126
9.5
Tuberías subterráneas
La ruta de tuberías subterráneas es algunas veces necesaria para cruzar una calle, tubería entre edificios, cruzando patios, etc. Los
factores que son importantes en el diseño de tubería plástica subterránea son los siguientes:
1.
2.
3.
4.
5.
6.
7.
Esfuerzos de flexión longitudinal.
Pandeo, arqueo.
Combeo.
Rigidez del suelo y geometría del suelo ( muy importante para suelos expansivos )
Carga viva y muerta.
Compresión de la pared, curveo y resistencia al corte.
Fuerza de levantamiento hidrostática (flotacion)
Modos de falla y colapso se describen a continuación como si se aplicaran a tubería plástica. (referencia 8):
Figura 9.4
1.
2.
3.
4.
5.
6.
7.
Modos de falla en tubería subterránea.
Socavación debida a la deflexión ( ver fig 9.4 a )
Compresión de pared(tipo anillo) debido a la deformación en A ( ver fig 9.4 b )
Pandeo: (a) elástico y (b) plástico. En estado de pandeo se muestra como en la figura 9.4 c
Flexión tipo viga ( fig 9.4 d )
Tensión longitudinal ( a lo largo del eje ) ( ver fig 9.4 e )
Corte directo ( ocurriendo en la interface duro-suave del terreno )( ver fig 9.4 f )
Falla en la junta ( ver figura 9.4 g)
127
Las perdidas de transferencia de calor de una tubería sepultada llegan a ser mas importantes en el caso de tuberías de aceite
calentado, ó en el caso de tuberías de vapor subterráneas para mantenerlas frías en paso de peatones y autos. Ecuaciones para
calcular la transferencia de calor en tuberías sepultadas se dan en la referencia 3.
Diseño de tuberías subterráneas
Diseñar la siguiente tubería subterránea. Asumir que datos son necesarios; la profundidad del cubrimiento = H = 3 pies; el ancho
de la trinchera = 2 pies 6 pulgadas; el material es ASTM A53 grado B; el mínimo esfuerzo de cedencia especificado es 35 000 psi a
145°F. Ver figura 9.5. El diámetro exterior de la tubería incluyendo aislamiento es 12”.
Asumir que el coeficiente de fricción entre la tubería y el terreno es 0.3.
La densidad de la arcilla saturada del terreno ω = 100 lb/
La tubería contiene aceite combustible # 6 13 API con gravedad especifica 1.2
Figura 9.5
Tubería sepultada con dimensiones de trinchera.
Etapas:
1.
Calcular la resistencia a la fricción
2.
Calcular la fuerza térmica , después calcular el esfuerzo longitudinal .
Encontrar el punto de ningún movimiento, el cual es = .
Calcular esfuerzo en la espira, esfuerzo flexor debido a la carga de tierra, el esfuerzo radial debido a la presión, y los
esfuerzos de temperatura debidos a la temperatura de operación.
Calcular el esfuerzo combinado de los esfuerzos en el inciso (4) usando la teoría de la máxima deformación.
Hallar el esfuerzo máximo permisible usando el código B31.4,( tubería de transporte de líquidos )
Para un diseño apropiado el esfuerzo combinado debiera ser menos que el esfuerzo máximo permisible.
3.
4.
5.
6.
7.
.
Primero, calcular la carga en la tubería desde el relleno
= carga sobre tubería, libras/ pie =
ω
.
(9.6)
128
Donde
= coeficiente de carga =
(9.7)
donde k = Relación de presión unitaria lateral entre presión unitaria vertical.
m´=m= coeficiente de fricción entre el material de relleno y la zanja ≤ m, donde m es el coeficiente de friccion interna
del relleno.
H = altura del relleno arriba dl tope de tubería, pies.
= ancho horizontal de la trinchera, pies.
Los valores del coeficiente de carga pueden ser tomados del diagrama en la figura 9.6 (referencia 7).
Figura 9.6
Coeficientes de carga
para conductos trinchera.
129
Etapa 1.
Calculo de resistencia de fricción (unidades lb/pie):
= carga sobre tubería desde el relleno negando el movimiento de la carga.
Permita que
Usando la formula de Marston :
donde
(9.6)
ω
= coeficiente de carga. Se lee en la grafica de la figura 9.6
= 1.0 x 100 x 2.5 x 2.5 = 625 lb/pie
=1
para
=
.
= 1.2
ω = densidad del terreno = 100 lb/
= ancho horizontal de la trinchera, 2.5 pies.
Altura del contenido = (peso de agua) gravedad especifica = (21.69) 1.2 = 26 lb/pie
Peso aislamiento = 5.38 lb/pie
Peso tubería de metal = 28.55 lb/pie
Peso total de la tubería = 625 +26 +5.38 +28.55 = 685 lb/pie
Factor de resistencia = m(peso total) = 0.3 ( 685 ) = 205.5 lb/pie
Etapa 2 y 3.
Punto de ningún movimiento:
La fuerza de fricción se opone a la fuerza térmica; en el punto de ningún movimiento, la fuerza de fricción es igual a la
fuerza de expansión térmica.
Esfuerzo longitudinal =
= Eα ( -
)-
(9.8)
Donde E = 27.9 x 10 psi
v = relación de Poisson = 0.3
D = 8.625 pulg
α= coeficiente lineal de expansión térmica
= 145°F
= 80°F
t = 0.322 pulg
P = 300 psig
La ecuación 9.8 proviene del código de tubería B31.4 ( referencia 3 en el capitulo 4 ). La sección 419.6.4 del código de
transporte de líquidos. Esta ecuación es para tubería sujeta, en este caso a causa de la tubería subterránea:
= 27.9 x 10 (6.5 x 10 )(145-80) - 0.3(300)
.
.
.
= 11 787 - 0.3 ( 3 717 ) = 10 669 psi
130
La fuerza de expansión térmica
=
( area de metal) = 10 669 ( 8.4 ) = 89 625 lb
Distancia del punto de ningún movimiento desde el punto de entierro =
= 436 pies
.
La figura 9.7 muestra la distancia de 436 pies desde el punto marcado de entierro.
Figura 9.7
Etapa 4.
Esfuerzos.
Esfuerzo anillo (
=
Para esfuerzo flexor (
Punto de cero movimiento en una tubería enterrada.
.
=
:
.
= 3 717 psi
.
), se usa la ecuación de Spangler :
= 0.177
Donde
(9.9)
.
= radio medio de la tubería = ( D - t )/2 = 4.1515 pulg. Los otros términos son los mismos de la ecuación 9.8
= 0.177
.
.
.
.
.
.
= 4 179 psi
.
:
Esfuerzo radial (
= P = 300 psi
:
Esfuerzo térmico (
= Eα ( - ) = 27.9 x 10 x 6.5 x 10 (145-80) = 11 787.83 psi
Esfuerzo circunferencial = =
+ ( esfuerzo térmico + esfuerzo flexor debido a la tierra)
= 3 717.87 + 0.3( 11 787.73 + 4 179 ) = 8 507 psi.
Etapa 5
Esfuerzo combinado ( S ): Usar la teoría de la máxima deformación.
2
S=
= 10 669
8 507
=
300
2 0.3 10 670 8 507
300 10 670
8 507 =
=11 327 psi
131
Etapa 6
Esfuerzo máximo permisible:
Usar tubería sujeta de acuerdo al B31.4.
Esfuerzo máximo permisible = 0.90 (mínimo de la tubería) = 0.90 ( 35 000 ) = 31 500 psi
Etapa 7:
El esfuerzo combinado de 11 327 psi esta debajo del esfuerzo permisible de 31 500 psi. Por lo tanto el diseño de la
tubería es seguro.
Diseño con presión externa
El diseño de recipientes cilíndricos que están sujetos a presión externa es remarcado en el código ASME sección VIII, División 1 UG28
(c).
Nomenclatura:
= Presion critica de colapso, psi
= Presion permisible, psi.
t = grosor de pared, pulg
E = modulo de elasticidad, psi
L = longitud entre soportes, pulg
= longitud critica, pulg
= Esfuerzo de cedencia, psi
= esfuerzo tangencial en la presión de colapso, psi
Factor A = /E
Factor B = /2
9.6
Esfuerzo de tubería bajo presión externa ( referencia 10)
El esfuerzo de tubería bajo presión externa es una función de las propiedades físicas del material de construcción, en la temperatura
de operación y sus parámetros geométricos tales como: longitud no soportada L, grosor de pared t, diámetro exterior , y la
tubería fuera de redondez.
El comportamiento de cuerpos cilíndricos de pared delgada bajo presión externa uniforme, varia de acuerdo al la longitud del
cilindro de acuerdo a lo siguiente:
1.
Cilindros muy largos:
La presión de colapso critica esta dada por :
2.2
La longitud critica
(9.10)
, la longitud no-soportada mínima mas allá de la cual
= 1.11
½
es independiente de L, esta dada por:
( 9.11)
132
2.
Cilindros intermedios con L <
:
La presión critica
dos relaciones características
y
. Para diseño practico,
=
3.
Cilindros cortos:
es una función complicada del contorno colapsado, y las
puede ser dado por la siguiente ecuación empírica:
.
.
(9.12)
El cilindro fallará en este caso por deformación plástica; la presión critica puede ser dada por:
=
(9.13)
Cartas ASME
Carta geométrica:
Para L > , el esfuerzo tangencial
escrito como:
=
= 1.1 E
Deformación =
Para L ≤
a la presión de colapso
(9.14)
= 1.1
, el esfuerzo tangencial
=
.
Deformación =
(dado por la ecuación 9.10), puede ser
(9.15)
a la presión de colapso
( dado por la ecuación 9.13 ) es:
.
(9.16)
=
.
.
(9.17)
Las ecuaciones 9.14 y 9.16 fueron impresas para desarrollar la carta geométrica en la figura UGO-28.0 del código ASME Caldera y
Recipiente a Presión, Sección VIII, División 1. Ver figuras 9.8 a y 9.8 b.
Cartas de material:
Estas cartas son realmente curvas esfuerzo-deformación para materiales a temperaturas de diseño ( el
valor de
en la abcisa y el valor de
en la ordenada ). (
se llama factor A y
se llama factor B
en la notación ASME ).
133
Figura 9.8 a
Carta geométrica para recipientes cilíndricos
Figura 9.8 b
Carta geométrica para recipientes cilíndricos
134
Figura 9.9 a
Carta para determinar el grosor de cuerpo de recipientes cilíndricos y esféricos bajo presión externa cuando están
construidos de acero austenitico [Aceros inoxidables:18Cr-8 NiMo,tipo 316; 18Cr-8 NiTi, tipo
321; 19Cr-8 NiCb, tipo 347; 25Cr-12Ni, tipo 309 ( hasta 1 100°F solo); 25Cr-20Ni, tipo 310; y 17Cr, tipo 430 (hasta
700°F solo)]( ASME sección VIII división 1)
Figura 9.9 b
Carta para determinar grosor de pared de recipientes cilíndricos y esféricos bajo presión externa, cuando están
construidos de acero austenitico ( 18Cr-8 Ni-0.03 de carbono máximo, tipo 304 L) ( ASME Sección VIII,Division 1)
135
Figura 9.10 a
Carta para determinar grosor de pared de recipientes cilíndricos y esféricos bajo presión externa, cuando están
construidos de acero al carbón o de baja aleación( Esfuerzo de cedencia especificado 24 000 psi, a pero no
incluyendo 30 000 psi) (ASME Sección VIII, División 1 )
Figura 9.10 b
Carta para determinar grosor de pared de recipientes cilíndricos y esféricos bajo presión externa, cuando están
construidos de acero al carbón o de baja aleación( Esfuerzo de cedencia mínimo especificado 30 000 psi (207 MPa) y
mas arriba ) y aceros inoxidables tipo 405 y 410 (ASME Sección VIII, División 1 )
136
La presión permisible puede ser obtenida por el uso de la siguiente relación:
=B=
Dejemos que
=3
=
( factor de seguridad = 3 )
= B
(9.18)
La ecuación 9.18 es la misma que la ecuación de la sección VIII subseccion UGO-28 ( c ) -1.
Diseño práctico usando las cartas ASME: Determine el grosor de tubería T bajo presión externa ( D/t ≥ 10).
Etapa 1. Asumir un valor para t y determinar las relaciones L/D y D/t.
Etapa 2. Determine el valor del factor A de la carta geométrica( usando los valores obtenidos en la etapa 1 )
Etapa 3. Determine el valor B por el uso de la carta de material apropiado, y el valor del factor A obtenido en la etapa 2.
Etapa 4. Calcular la presión externa permisible , usando la ecuacion 9.18
puede ser
Etapa 5. Para valores de A cayendo a la izquierda de la línea aplicable material/temperatura; el valor de
determinado por la siguiente formula:
= AE
(9.19)
( nota: para D/t < 10 use el procedimiento remarcado en ASME UG-28 ( c ) -2 )
Etapa 1. Asumir un valor para t y calcular B:
B=
Etapa 2. Hallar el factor A usando la carta de material apropiado y el valor de B obtenido arriba; Si el valor del factor B es
menor que el valor enlistado en la carta, el factor A es dado por:
A=
.
Etapa 3. Determine el valor de L/D por el ingreso del factor A y la curva apropiada D/t en la carta geométrica: la Longitud
máxima sin refuerzo se obtiene por la multiplicación del valor L/D por D. ( si no hay intersección entre la
proyección vertical de A y la curva D/t, entonces los refuerzos no son requeridos para ninguna longitud).
Ver el ASME Sección VIII, división 1, subseccion UGO-29 para el diseño de anillos de refuerzo.
137
Ejemplo ( copia del apéndice L del ASME, sección VIII, división 1 )
9.7
Recipientes bajo presión externa.
Nota:
Las líneas sobre la figura UGO-28.0 del apéndice V (fig 9.8 a y b) expresan una relación geométrica entre L/
y
para
cuerpos cilíndricos y tubos, la cual es común para todos los materiales. Esta carta es usada solo para determinar el factor
A, cuando el factor A no es obtenido por la formula en el caso especial cuando
< 10. ( ver UG- 28 ( c )-2)
Las tablas que permanecen en el apéndice V son para materiales específicos, o clases de materiales, y representan
diagramas de pseudo esfuerzos de deformación, conteniendo factores de seguridad apropiados relativos al fluo elástico y
colapso elástico.
Referencia del ASME Sección VIII, UA - 270
(a )
Cuerpo cilíndrico bajo presión externa. ( Un ejemplo del uso de las reglas en UG-28 ( c ) ) ( ecuación 9.18 )
Dado: Torre fraccionadora de 14 pies de diámetro interior por 21 pies de longitud, de línea curva a línea curva, con
bandejas fraccionadoras, y operando bajo vacio a 700°F. La torre esta construida de acero al carbón SA-285 grado C.
La longitud de diseño es 39 pulg.
Se requiere:
Grosor del cuerpo t.
Solución:
Etapa 1.
=
Etapa 2, 3
.
D
= 0.231
Etapa 6.
=
.
.
= 540
Entrar a la figura UGO-28.0 en el apéndice V ( fig 9.8 a y 9.8 b) en el valor de
horizontalmente hasta la línea
Etapa 4, 5
Asumir diámetro exterior = D = 168.625 pulg
Asumir un grosor t = 0.3125 pulg
D
= 0.231. moverse
de 540, y leer el valor de A de 0.0005.
Entrar a la figura UCS-28.2 ( fig 9.10 b )en el valor de A = 0.0005 y moverse verticalmente hasta la línea
del material a 700°F. Moverse horizontalmente y leer valor de B de 6100 sobre la ordenada.
La máxima presión externa permisible ( ecuación 9.18 ) para el grosor de cuerpo asumido de 0.3125 pulg,
es:
=
Dado que
D
=
= 15.1 psi
es mayor que la presión de diseño P de 15 psi, el grosor asumido debiera ser satisfactorio.
138
9.8
Sistemas de tubería enchaquetada a presión.
Método de calculo del grosor del núcleo de tubería
Ejemplo 1
La tubería es de 4”Ø, operando bajo un vacio completo a 650°F; la presión externa es 100 psig; la longitud máxima
del carrete sin anillos de refuerzo es 10 pies 0 pulg. El material de tubería es acero inoxidable T 316 ASTM A-312
(fig 9.11).
Figura 9.11
Tuberia enchaquetada ( vacio en la tubería a presión )
Calcular el grosor del núcleo de tubería.
Etapa 1 Asumir el grosor de tubería como ced 10S ( 0.12 pulg)
(grosor mínimo) = 0.12 x 0.875 = 0.105 pulg( el .875 es el remanente del 12.5% de tolerancia de manufactura)
D (diámetro exterior) = 4.5 pulg
l (longitud del carrete) = 120 pulg
Asi
=
D
= 26.66
.
Etapa 2 Entrar el valor de
.
.
= 42.85
=26.66 (fig 9.8 b) en la figura UGO-28.0, del apéndice V, ASME Seccion III, división 1,
moverse horizontalmente hasta el
Para valores de
=
D
= 42.85 , y leer el valor A= 0.0006.
> 50 , entrar a la carta en 50 para determinar elvalor de la constante A.
Etapa 3 Entrar en la figura (fig 9.9 a) UHA-28.2 en el valor de A = 0.0006 y moverse verticalmente hasta la línea de
material para 650°F( interpolado entre las líneas de material de 400°F y 700°F). Moverse horizontalmente y leer B
de 6 700 sobre la ordenada.
Etapa 4 La presión máxima externa permisible ( ec 9.18)para la tubería, asumiendo tubo ced 10 S como nucleo, es:
= B
=
.
= 208 psig
Para valores de constante A cayendo a la izquierda de la línea material-temperatura aplicable, la presión externa máxima
puede ser directamente evaluada de la siguiente ecuacion:
=
(9.19)
139
Donde E = modulo de elasticidad del material a la temperatura siendo considerada.
La presión externa de diseño es 115 psig ( el nucleo a vacio completo y presión externa es 100 psig, la presión actuando en
la misma dirección se convierten en aditivas)
Puesto que,
Ejemplo 2
es mas grande que la presión de diseño 115 psig, el grosor asumido es por lo tanto satisfactorio.
La tubería es de 4”Ø, operando bajo presión interna de 125 psig a 650°F; la presión externa es 100 psig; la máxima
longitud del carrete sin anillos de refuerzo es 10 pies 0 pulg; el material del tubo es acero inoxidable tipo 316
ASTM- A312 ( ver fig 9.12)
Figura 9.12
Tuberia enchaquetada ( mas alta presión en la tubería de proceso )
Calcular el grosor del núcleo de tubería. Las etapas 1 a 4 son las mismas como en el ejemplo 1, los resultados son
derivados de las figuras UGO 28.0(fig 9.8 b) y UHA-28.2(fig 9.9 a) del apéndice V, ASME Seccion VIII, Division 1.
De la etapa 4 en el ejemplo 1, la máxima presión externa permisible ( ) para el núcleo de tubería ced 10 S es de 208 psig.
La presión de diseño externa (P) = 100 psig, en vista que es mayor que P, el grosor asumido es satisfactorio.
La presión externa es el factor gobernante para el diseño de seguridad del tubo núcleo en los sistemas de tubería
enchaquetada. Si no hubiera habido alguna presión externa, la tubería conduciendo 125 psg de presión de fluido podía
haber tenido pared de sección más delgada.
Para calcular el grosor de chaqueta, use la ecuación 2.1 ( del ASME B31.3, 304.1.2 )
Tubería recta bajo presión interna
El grosor de diseño para presión interna t será no menor que el calculado por la ecuacion 2.1, cuando t es menos que D/6 ( ver
capitulo 2 ):
t=
(2.1)
9.9
Unidades métricas
Las unidades métricas son usadas en la mayoría de los países del mundo, los códigos de diseño de tubería y estándares comienzan
comprometiéndose con las unidades métricas. En una futura edición las ecuaciones dadas en este libro quizá serán modificadas para
acomodar las unidades métricas. Todas las ecuaciones dadas aquí pueden ser usadas para diseño de tubería en unidades métricas,
por el uso de los factores de conversión apropiados ( ver tabla 9.9, la cual proviene del código de recipientes a prezion, ASME Seccion
VIII, Division 1 ). Después de calcular el grosor de tubería, , diámetro, etc, usando unidades Británicas, los valores estándar próximos
140
en el lado conservador en unidades métricas, pueden ser seleccionados. Se debe tomar precaución, para referirse a los códigos de
tubería y estándares de fuerza en cada país.
Tabla 9.9 a
Tablas de conversión sistema métrico internacional: lista de unidades SI para usarse en el código ASME para
calderas y recipientes a presion.
141
* Las relaciones son exactas en términos de las unidades base que son seguidas de un simple asterisco.
Τ Los factores están escritos basados en potencias base 10 , Por ejemplo 3.523907 E -2 = 3.523907 x 10 = 0.03523907
Tabla 9.9 b
9.10
Factores de conversión usados comúnmente ( para otros ver ASTM-380 )
Comportamiento del material a elevadas temperaturas ( referencia 10 )
Las elevadas temperaturas son aquellas en las cuales los efectos de deslizamiento son significativos; la figura 9.13 es el resultado de
un espécimen a tensión uniaxial sujeto a un nivel de esfuerzo de carga inducido, en una temperatura (baja) de prueba dada. Ambos
esfuerzo y deformación alcanzan su valor máximo al mismo tiempo, y permanecen constante en los valores máximos después de eso
( a lo largo que la carga es mantenida ): Cuando la temperatura de prueba es lo bastante alta, la deformación se incrementara con el
tiempo, y posiblemente has ta la fractura después de la aplicación de la carga como se muestra en la figura 9.14. En este caso el
efecto de deslizamiento es significativo. Si, por el otro lado, la prueba uniaxial a elevada temperatura es una a la cual el espécimen es
deformado a una cantidad fija y entonces mantenida constante. La historia esfuerzo-deformación seria algo similar a la figura 9.15. La
142
reducción de esfuerzo como se muestra en esta figura es llamado el esfuerzo de esfuerzo de relajación debido a los efectos de
deslizamiento.
De esta figuras puede fácilmente ser visto que a elevadas temperaturas, el comportamiento del material es una función del esfuerzo,
temperatura y tiempo.
Figura 9.13
Esfuerzo y deformación contra tiempo a baja temperatura
Figura 9.14
Esfuerzo y deformación contra tiempo a elevada temperatura ( efectos de deslizamiento )
Figura 9.15
Esfuerzo y deformación contra tiempo a elevada temperatura ( esfuerzo de relajación )
Aplicación de los datos de deslizamiento al diseño de tubería ( referencia 2 )
A temperaturas debajo del rango de deslizamiento, los valores de esfuerzo permisible están establecidos en el valor mas bajo de
esfuerzo obtenido del uso del 25% de la fuerza mínima ultima especificada a la temperatura del cuarto, ó 25% de la fuerza ultima
mínima esperada a la temperatura, ó 62.5 % del esfuerzo de cedencia mínimo esperado para 0.2% de desplazamiento en temperatura.
Para material de atornillado, los valores de esfuerzo estuvieron basados sobre 20% del esfuerzo tensil mínimo, ó 25% del esfuerzo
de cedencia para 0.2% de deslizamiento, cualquiera sea menor. ( Es reconocido que a los tornillos generalmente se espera funcionen
a esfuerzos arriba del valor de diseño, como se a distinguido de otras partes ).
Ningún crédito es permitido para aumentar las propiedades tensiles por tratamientos térmicos especiales.
A temperaturas mas altas, donde el deslizamiento gobierna, los valores de esfuerzo estuvieron basados sobre el 100% del esfuerzo
para producir una tasa de deslizamiento de 0.01% para mil horas , los valores de manera tal seleccionados están siendo basados
143
sobre un promedio conservador de muchas pruebas reportadas como evaluadas por el Subcomité, el mayor peso esta siendo dado la
las pruebas de largo tiempo en la evaluación de datos. En adición a los requerimientos de esfuerzo de deslizamiento arriba
estipulados, los valores de esfuerzo fueron también limitados al 100% de los esfuerzos para producir ruptura al final de las 100 000
horas, los valores de manera tal seleccionados están siendo basados sobre un promedio conservador de muchas pruebas reportadas
como evaluadas por el Subcomité. Sin embargo, en la mayoría de los casos, el esfuerzo de deslizamiento esta lejos debajo del
esfuerzo de ruptura. También, en unos pocos casos , el Subcomité ha provisto valores de esfuerzo sin datos de prueba de ruptura
sobre la composición especifica, tales aprobaciones se basan sobre pruebas de materiales de composición similar.
En el rango de transición de temperaturas, los esfuerzos permisibles fueron limitados a valores obtenidos de una curva suave
juntando los valores para los rangos de baja y alta temperatura, la curva descansando sobre o debajo de la curva de 62.5% del
esfuerzo de cedencia mínimo esperado a la temperatura.. En la selección de los valores de esfuerzos , en el rango donde un
porcentaje del esfuerzo tensor o el esfuerzo de cedencia gobiernan, las limitaciones indicadas arriba han sido repudiadas en ciertos
casos ( Este valor de 100% concierne al Código de recipientes a presión sin fuego. En el código de calderas de potencia, esta
limitación de esfuerzo es 60% del promedio ó 80% del esfuerzo mínimo para producir la ruptura en las 100 000 horas como se
reporta en los datos de prueba) como fue sentido que los valores mas altos de esfuerzo podían ser justificados cuando la deformación
no fuera en si misma objetable, provistos todos los otros requerimientos que hayamos encontrado.
En el diseño de equipos no cubiertos por lis códigos, los valores de esfuerzo de diseño pueden ser decididos con los manufactureros y
vendedores de tubería, y debieran estar basados sobre los mejores datos asequibles mas un conocimiento de la expectativa de vida
del equipo, también como las condiciones de operación, y el posible daño al personal. Las reglas que generalmente se siguen son:
a.
b.
Hasta 750°F ó 850°F, 25% del esfuerzo tensil de corto tiempo y que no exceda de 62.5 % del esfuerzo de cedencia.
Arriba de 900°F, 100% del esfuerzo para producir una tasa de deslizamiento en la segunda etapa de 0.01% en 1 000
horas, ó 80% de los esfuerzos para producir ruptura en 100 000 horas, cualquiera es menor.
9.11
Recubrimientos refractarios
Los recubrimientos refractarios se usan en hornos de secado, hornos de coque, fogones, y chimeneas, para proteger las partes
metálicas de la exposición directa de temperaturas altas ( figura 9.16 ). Los refractarios necesarios para resistir muy altas
temperaturas sin fundirse, debieran tener necesariamente propiedades mecánicas y de transferencia de calor, no debieran reaccionar
con el medio en el interior del fogón, y grandes cantidades necesitan ser asequibles a bajo precio ( referencia 5 ). Basados en sus
propiedades químicas, los refractarios son clasificados como: acidos ( silica ), básicos ( magnesia ) y neutros ( mineral de cromo ). La
forma ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||estándar para refractarios es el ladrillo.
En el diseño de un laminador de acero, tuberías de diámetro grande inclinadas se usan. Es de importancia el calculo de peso a ser
soportado en los puntos de apoyo ( figura 9.16 )
Densidad del refractario
Densidad del acero
Densidad del aislamiento
= 40 lb/
= 0.283 lb/
=11 lb/
144
Diámetro interior del refractario = 39 pulg
Diametro exterior del tubo
= 48 pulg
Diametro exterior del aislamiento = 52 pulg
Figura 9.16
Recubrimiento refractario
Peso por pie = peso de ( refractario + metal tubería + aislamiento )
=
47
39
12
+
48
47
12 (0.283) +
(9.20)
52
48
12
= 151.55+255.83+21
= 428.46 lb/pie
Ejercicios
1.
¿Verdadero o falso?
(a) Los muelles fríos no pueden ser usados para reducir el momento sobre un recipiente.
(b) El modulo caliente de elasticidad pude ser usado para calculo de esfuerzo.
(c) Para calculo de espaciado, la máxima deflexión permitida adentro de la planta es 1 pulgada.
(d) El código de tubería B31.1 permite el uso de SIF en-plano y fuera de plano.
(e) El refuerzo (pad) es necesario cuando el área requerida es mas pequeña que el área removida.
(f) Cuando hay presión interna incluida decrece el valor del SIF para un codo.
(g) Cuando los efectos de bridas están incluidos para un codo, el factor de flexibilidad se reduce.
(h) Las espiras de expansión toman menos espacio comparado con una junta de expansión.
2.
¿Verdadero o falso?
(a) El muelleo frio solo puede ser aplicado a tubería caliente .
(b) Para calculo de espaciado el modulo caliente debiera ser usado.
(c) La presión interna incrementa el factor de flexibilidad para un codo.
(d) Las espiras de expansión son mas seguras que las juntas de expansión.
(e) El crecimiento de la boquilla de un recipiente es para ser incluido en cálculo de esfuerzos.
(f) El diseño de tubería (refinería) esta gobernado por el código ASME.
145
(g) El diámetro exterior de una tubería de 6”Ø (diámetro nominal) es 6.5”.
(h) El diámetro de salida es mas grande que el diámetro de entrada de válvulas de alivio de presión.
3.
Una tubería subterránea de 12”Ø ced 40 ASTM-A53 grado B tiene las siguientes condiciones:
Temperatura de operación: 175°F
Temperatura de instalación: 70°F
Profundidad de la fosa: 3 pies 6 pulg
Gravedad especifica del contenido: 0.73
Presion de operación: 375 psig
(a) ¿Dónde esta la localización del anclaje natural?
(b) ¿La cantidad de expansión térmica en el extremo? ( el coeficiente de friccion = 0.75)
4.
Calcular la fuerza de expansión dinámica con el sistema de descarga abierto.
Flujo = 165 000 lb/hr
Área del orificio de la válvula = 55
J = 778 pie-libra/BTU ; g = 32.2 pie/
Temperatura = 650°F; PR 0 155 psig
= 1 374 BTU/lb ( de las tablas de vapor)
a = 823 BTU/lb ; b = 4.33
la línea de descarga es 6”Ø ced 40.
5.
Un compresor de gas reciprocante de doble acción tiene una tasa de velocidad máxima de 650 rpm, con una presión de
pulsación limitada a 13 psi. La tubería de descarga es de 3”Ø ced 40. ¿Cuál será la fuerza de pulsación?, ¿Cuál es el máximo
espaciado (claro) entre soportes de tubería? =3.02
.
6.
Una tubería de 20”Ø de acero al carbón tiene un grosor de pared de .25”. El mínimo esfuerzo de cedencia especificado es
47 000 psi a una presión de diseño de 600 psig. La temperatura de diseño es 170°F y la temperatura de invierno es 25°F.Si
el esfuerzo flexor es 9 200 psi, ¿ Cual es la temperatura de conexión? ( el rango de temperatura entre verano e invierno es
25 a100°F.
7.
Una tubería de crudo de 18”Ø va a ser diseñada con una presión de operación de 1 300 psi, y una temperatura de operación
de 170°F. La tubería que se usara es API-grado X52 soldada por resistencia eléctrica. La eficiencia de junta de la soladura es
85%. El esfuerzo mínimo permisible especificado es 53 000 psi. La temperatura de contruccion esperada es de 75°F. Si el
esfuerzo flexor es 9 750 psi, ¿Cuál será el grosor de pared de la tubería?.
8.
Si la tubería del ejemplo 7 estuviera sujeta, ¿ Cual será el esfuerzo longitudinal en el punto de anclaje?
146
9.
Para una tubería de 20”Ø la presión de operación máxima requerida es 670 psig, y la temperatura de operación máxima
esperada es 165°F. El material del tubo será API-5Lx, grado X52 con un esfuerzo de cedencia minimo especificado de 49 000
psi. Basado en la presión el grosor de pared calculado es 0.25”. Si la temperatura de conexionx tiene que ser 75°F con un
esfuerzo flexor de 7 700 psi, Calcular el esfuerzo en la tubería.
Referencias
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
Información sobre válvulas se obtiene de:
Vogt Forged Steel Valves, Fittings, Union, Flanges, Catalog F-12
Powell Valves, Catalog 150
Walworth Valves, Catalog 130
Crane Valve Fittings, Catalog 60
King, C. Reno and Sabin Croker. Piping Handbook, New York: Mc Graw Hill
Amir,S.J. “Calculating heat transfer from a Buried pipeline” Chemical Engineering (August 4,1975)
Schweitzer, Handbook of corrosion Resistant Piping. Industrial Press
Nord, Melvin Textbook of engineering Materials, New York: Wiley
ANSI Standard A58.1, Wind Loads for Buildings and Other Structures.
Leonards,G.A. Foundation Engineering, New York: Mc Graw Hill
Owens-Corning, Plastic Pipe Program
ITT Grinnell “ Pipe Hangers Design an Engineering” in Weght of Piping Materials, revised in 1979
Truong,Q.N. “ International Piping Conference”, at Texas A & M University, Texas, April , 1983.
147
CAPITULO Diez
Componentes Nucleares.
Código ASME Sección III
10.1
Cargas de diseño y limites de servicio.
El código de diseño de componentes nucleares, ASME Sección III (referencia 5 en el capitulo 4) requiere que los efectos de terremoto
se incluyan en el diseño de tubería, soportes de tubería, y sujeciones (ver sección III, subseccion NC-3262, efectos dinámicos). Las
cargas, los movimientos incluyendo los de anclaje de terremoto, y el numero de ciclos a ser usados en el análisis, son parte de las
especificaciones de diseño. Los esfuerzos resultantes de estos efectos de terremoto deben ser incluidos con el peso, presión u otras
cargas aplicadas cuando se esta haciendo el análisis requerido. La sección III también requiere que sean especificadas las cargas de
diseño (NC-3611.2(b)), y cargas de servicio (NC-3611.2(c)). Las cargas de servicio están agrupadas con limites de servicio, como nivel
A ( ecuaciones 10.10 y 10.11 ), nivel B ( ecuación 10.9U ), nivel C ( ecuación 10.9 E ), y nivel D ( ecuación 10.9 F ). Ver también el
capitulo 6 para una breve explicación de estos limites de servicio. Los limites de servicio B, C y D requieren la inclusión de cargas de
terremoto. Las cargas de diseño están dadas por la ecuación 10.8. Las ecuaciones 10.4 a 10.7 han sido eliminadas de manera tal que
los números de ecuaciones usados en (la tabla 10.2) serán lo mismo que esos usados en la sección III (referencia 5 en el capitulo 4).
La tubería nuclear esta clasificada como clase 1 (NB), clase 2(NC), y clase 3 (ND). La tubería que conecta el reactor y el generador de
vapor y otras tuberías criticas caen bajo el análisis clase 1, el cual esta fuera del alcance presente de este libro. Un análisis muestra
de este sistema de tubería nuclear clase 1 preparado por el comité de ASME de calderas y recipientes, sería gran ayuda para lecturas
adicionales de diseño clase 2 que se presentan aquí. La mayoría de compañías diseñan conservadoramente bajo guias de tuberías
clase 3 y clase 2.
10.2
Flexibilidad y factores de intensificación de esfuerzos.
La tabla es una reimpresión de la tabla NC-3000 del ASME sección III. Note que solo una ecuación para SIF correspondiente para los
valores mas altos de 0.9 / es dada. El código nuclear también da ecuaciones para calcular SIF de conexiones de ramal, basadas
también sobre las dimensiones del ramal, juntas soladas, transiciones cónicas a 30° y reducciones concéntricas.
Ejemplo 1
Calcular el SIF para una conexión dada de copa soldada en la conexión de un ramal. ( las mismas ecuaciones se aplican para
un medio cople enchufable soldado y un cople soldado). El cabezal o tubería que corre es de 12”Ø con un grosor de 0.375
pulg. El ramal es 6”Ø con un grosor de 0.28 pulg ; con un diámetro exterior de la soldadura de copa = OD del ramal + 2
(grosor de la copa soldada).
148
Tabla 10.1
Factores de intensificación de esfuerzo ( diseño NC-3000 ) continua
149
Tabla 10.1
Factores de intensificación de esfuerzo ( diseño NC-3000 ) continuacion
1.
Se aplica la siguiente nomenclatura:
r = radio medio del tubo, pulg. ( tubería machimbrada para tes y codos )
= grosor de pared nominal del tubo, pulg ( tubería machimbrada para tes y codos, ver nota 9 )
R = radio de curvatura de la curva o codo, pulg
θ = la mitad del Angulo entre los ejes de dos gajos adyacentes
s = espaciado entre centros de línea de gajos, pulg.
= grosor del refuerzo, pulg
δ= desacople, pulg
= diámetro exterior,pulg
2.
Los factores de flexibilidad k y factores de intensificación i se aplican para curvas en cualquier plano y no serán tomados en ningún caso
menores que la unidad. Ambos factores se aplican sobre la longitud del arco efectivo ( mostrado en líneas de centro gruesas en los bocetos ) para
curvas y codos de gajos, y para los puntos de intersección de tes. Los valores de k e i se pueden leer directamente ( tabla 4.3 b ) introduciendo
las h características computadas de las ecuaciones dadas.
Cuando se colocan bridas en uno o ambos extremos, los valores de k e i serán corregidos por el factor c dado abajo, el cual puede ser leído
directamente de ( tabla 4.3 b ), entrando la h calculada.
3.
4.
5.
6.
ambos extremos bridados c=
Una brida en un extremo c=
También incluye juntas simples de gajos.
Cuando >1.5 , h = 4.05 /r.
La ecuación se aplica solo si se encuentran las siguientes condiciones:
(a) Se cumplen los requerimientos de area de refuerzo del NC-3643.
(b) El eje de el ramal esta normal a la superficie de la pared del cabezal.
(c) Para conexiones de ramal en una tubería, la distancia de arco medida entre los centros de línea de dos ramales adyacentes a lo largo de la
superficie del cabezal, no es menor que tres veces la suma de sus radios interiores en la dirección longitudinal, ó no es menos que dos veces la
suma de sus radios a lo largo de la circunferencia del cabezal.
(d) El radio de la curva interior ( fig NC-3673.2(b) ) ( fig 10.1 ) esta entre 10 y 50% de .
(e) El radio exterior no es menor que la mas grande de /2, ( + y )/2 ( fig NC-3673.2(b)-2) (fig 10.1 )boceto (c) ó /2.
150
(f) El radio exterior no es menos que el mas grande de
(1)
0.002 θ
(2)
2
veces el desfase para las configuraciones mostradas en las figuras NC- 3673.2(b)-2 (fig 10.1) bocetos (a) y (b)
/
50 y ´ /
0.5
(g)
7.
8.
9.
La ecuación se aplica solo si se cumplen las siguientes condiciones:
(a) El Angulo del cono α no exceda de 60°, y la reducción sea concéntrica.
(b) El mas grande de / y / no exceda de 100.
(c) El grosor de pared no sea menos que de un extremo a otro del cuerpo de la reducción, excepto en e inmediatamente adyacente a la
porción cilíndrica en el extremo pequeño, donde el grosor no será menor que .
Los factores mostrados se aplican a flexion,; el factor de flexibilidad para torsión es igual a 0.9.
El diseñador esta avisado que los codos fundidos soldados a tope pueden ser considerablemente mas pesado de pared que ese de la tubería con el
cual ellos son usados. Grandes errores puede ser introducidos a no ser que el efecto de estos grosores mas grandes sean considerados.
Continua el ejemplo 1 de la pagina 147
El SIF A esta dado por:
Donde
½
SIF = 1.5
´
SIF ≥ 1.0
≤ 50
´
´
≤ 0.5
(10.1)
radio medio del cabezal, pulg.
´ = radio medio del ramal, pulg.
= Grosor de pared nominal del cabezal, pulg.
= Grosor de pared nominal del ramal, pulg.
= Radio exterior del cople o copa, pulg. ( radio exterior de la conexión ramal )
La figura 10.1 ( del ASME Sección III, subseccion Figura NC- 3673.2(b)2 ) muestra cuatro conexiones de ramal para las cuales
la ecuación 10.1 se aplica.
OD del cabezal = 12.75 pulg, y un grosor = 0.375 pulg.
OD del ramal = 6.625 pulg y un grosor = 0.28 pulg.
=
.
.
= 6.025 pulg
´ =
.
.
= 3.0325 pulg
= Radio exterior del cople o copa = [ 6.625 + 2 (.625) ]0.5 = 3. 9375 pulg
= 1.5
´
½
´
= 1.5
6.025
3.0325 ½
0.28
3.0325
0.375
6.025
0.375
3.9375
=
= 1.5 (6.637)(0.709)(0.7466)(0.77) =
= 3.89
151
Figura 10.1
Dimensiones del ramal ( ASME sección III, NC 3673.2(b)-2 )
Las ecuaciones de arriba se aplican solo si las condiciones de la nota 6 de la tabla 10.1 son encontradas. Note que
´
= 0.5033, lo
cual excede el limite de 0.5 ligeramente.
Los valores de intensificación de esfuerzo debieran ser tomados como el mas alto del valor calculado arriba por la ecuacion y el SIF
del tubo ramal. El SIF para el tubo recto asumiendo que la soldadura enchufable será igual a 2.3.
Ejemplo 2
Calcular el SIF para la reducción concéntrica con un diámetro mayor de 6.625 pulg y un diámetro menor de 4.5 pulg. El grosor del
lado mas grande es 0.28 pulg , y del lado menor es 0.237 pulg ( fig 10.2 )
Figura 10.2
Reducción concéntrica.
152
El ángulo del cono de reducción = α=
.
=
.
.
=
(0.19318)= 11.138 °
Checar para el uso de la ecuacion de SIF en la tabla 10.1, nota 7.
=
.
.
= 23.66 < 100
α= 11.138 ° < 60°
Usar
OK
=
.
.
= 18.98 < 100
OK
OK
SIF = 0.5 + 0.01 α
ó
SIF = 0.5 + 0.01 (11.138)
.
.
≤ 2.0
(10.2)
=1
SIF = 1
10.3
Análisis para evaluación de esfuerzos de tubería Clase 2 ( Componentes NC )
La tabla 10.2 nos da el criterio para el análisis riguroso y comprensivo para la tubería clase 2 ( referencia 1 ). A continuación se
explican las abreviaturas usadas:
DW= cantidad de peso
CS= Muelleo frio
PL= Precarga
VT= empuje de válvula
WH= Golpe de agua
E1= Carga base de operación para terremoto
E2= Carga de corte de seguridad para terremoto
J1= Golpeo Jet
S1= Movimiento de anclaje sísmico debido al OBE
S2= Movimiento de anclaje sísmico debido al SSE
BS= Asentamiento edificio
Ti= Carga térmica
CP= Movimiento de contención debido a la presion después del DBA
CT= Movimiento de contención debido a la temperatura después del DBA
P=
Presion de diseño, psi.
= Diametro exterior de tubo, pulg.
= Diametro interior de tubo, pulg.
i = Factor de intensificacion de esfuerzo ( i≥1, 0.75 i ≥1 )
0.75 i no puede ser menos que 1.
153
Z=
AVC=
DM=
DBA=
=
=
=
Modulo de seccion,
Coeficiente de válvula active ( 0.75 a 0.9 )
Movimiento dinámico
Diseño base accidente.
Esfuerzo básico permisible a la mínima temperatura (fría)psi.
Esfuerzo básico permisible a la temperatura de diseño, psi ( ver Sección III para valores )
Rango de esfuerzos permisibles ( ec 4.1 )
=Presion pico, psi.
= Esfuerzo de cedencia, psi
PT= presión de corrimiento del fuelle. lb
=
bajo condición de falla. Pie-lb
Tabla 10.2
Criterios para la evaluación de los esfuerzos de tubería clase 2 ( tuberías, categoría I y II )
Notas de la tabla 10.2:
1.
Todos los momentos son calculados en los tres componentes
la suma de los cuadrados ( SRS ).
,
2.
,
,
y
. Los términos
,
y
representan la raíz cuadrada de
=
El muelleo friono debiera ser usado para reducir esfuerzos. Las cargas de muelleo frio pueden ser consideradas en la evaluación de cargas en
soporte y equipo.
154
3.
4.
5.
6.
7.
8.
9.
10.
11.
La evaluación de las ecuaciones 10.9U y 10.9F no es requerida para la tubería de categoría II ( donde solo se requiere limitada integridad
estructural ).
El código ASME Sección III, División 1, Subseccion NC-3652. Análisis de tubería.
En general, las cargas de golpeo Jet no son asequibles an la fase de análisis, y por eso no se incluyen en la evaluación para la condición de falla.
El termino SAM también conocido como (Dynamic Anchor Movements) movimientos de anclaje dinámicos S1 y S2, pueden ser incluidos en las
ecuaciones 10.9 y 10.10 pero no ambas.
Para condición normal o recalcada, Las ecuaciones 10.8 ó 10.9U más las ecuaciones 10.10 ó 10.11 deben ser satisfechas.
La ecuación 10.10 a se aplica a movimientos no repetidos, tales como los de asentamiento de edificio.
para casos de emergencia ó falla (secundaria) en la ecuación 10.10ª debe incluir a ambos, movimiento térmico de contención
El momento
(CT) y movimiento de contención de presión (CP) después del diseño base accidente (DBA).
Los esfuerzos de presión pueden también ser calculados por el uso de la formula P /2(grosor).
La tabla 10.2 puede tambien ser usado conservadoramente para tubería clase 3 ( componentes ND )
10.4
Frecuencia Natural
Si la frecuencia natural de un sistema de tubería esta en, ó cerca de la frecuencia de una fuente de excitación, por ejemplo, un
compresor, las amplitudes resultantes pueden inducir esfuerzos de flexión que conduzcan a una prematura falla por fatiga. Debe
haber un necesario criterio de diseño, por eso, las frecuencias naturales en un sistema de tuberías deben ser significativamente mas
altas que , ó diferentes de las frecuencias de la fuente exitante.
La frecuencia natural en ciclos por segundo esta dada por la ecuacion 10.3.
=
(10.3)
Donde L = longitud de tubería, pies.
E = modulo de elasticidad. Psi
I = momomento de inercia,
W = peso de tubería, lb/pie
α = valor dependiendo sobre las condiciones finales y el modo bajo consideración. Ver tabla 10.3 para valores de α.
Tabla 10.3
Calculo de frecuencia natural ( valores
para la ecuación 10.3 )
155
10.5
Sistemas de tuberías a ser analizados
Los esfuerzos de tuberías normalmente serán realizados para sistemas de tuberías en las categorías siguientes:
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
Líneas de 3”Ø o mas grandes : (a) conectadas a equipo rotatorio, ó (b) sujetas a asentamiento diferencial de equipo
conectado y/ó soportes, ó (c) con temperaturas menores que 20°F.
Líneas conectadas a equipo reciprocante.
Líneas de 4”Ø o mas grandes conectadas a enfriadores de aire, generadores de vapor, ó secciones de tubos de calentamiento
a fuego.
Líneas de 6”Ø ó mas grandes con temperaturas de 250°F y mas altas.
Líneas con temperaturas de 600°F y mas altas.
Líneas de 16”Ø y mas grandes.
Líneas de material de aleación.
Líneas de alta presión.
Líneas sujetas a presión externa.
Tubería de pared delgada, o ductos de 18” de diámetro y mayores, teniendo una relación de diámetro exterior entre grosor
de pared de mas de 90.
Las líneas requiriendo artificios de expansión apropiados, tales como juntas de expansión y coples Victaulic.
Líneas de proceso subterráneas.
Tuberías de proceso recubiertas internamente.
Líneas en servicio critico.
Sistemas de alivio de presión.
Información necesaria para análisis de esfuerzo de tubería
1.
2.
3.
4.
5.
6.
7.
8.
9.
Diámetro exterior de tubería, grosor de pared ( ó diámetro nominal, numero de cedula ) ( apéndice A4 )
Temperatura, presión interna.
Material de tubería ( serán seleccionados para el material el coeficiente de expansión, modulo de Young, y densidad )
(Apendice A2).
El material y grosor de aislamiento ( si no se dan, los grosores estándar para silicato de calcio serán seleccionados )
La gravedad especifica del contenido.
¿La carga de viento será considerada? Si si, la dirección de aplicación es importante.
Cualquier traslación de anclaje inicial, Δx en pulg, Δy en pulg, Δz en pulg ( para torres, intercambiadores, etc, es
importante la traslación inicial de boquilla )
Tolerancia de corrosión para la tubería, pulg.
Rango de presión de la brida, psi (ANSI B16.5)
156
10.
11.
12.
13.
14.
15.
16.
17
El peso estándar de válvula y bridas será usado ( referencia 1 en el capitulo 9 ) (para válvulas especiales marque el peso en
el isométrico de esfuerzo de tubería.
En el análisis de tubería Nuclear, el ramal también necesita ser incluido con el cabezal, si el área del la razón de momento
de inercia / < 40. En otras palabras no se permite el desacople. Cheque el criterio de la compañía para la razón
que se va a usar.
Preguntar por cualquier carga permisible de los manufactureros de bombas, turbinas, compresores. ( de los dibujos de
vendedores de equipo)
Preguntar por cualquier preferencia para espiras de expansión, juntas de expansión,etc; si es necesario (capitulo 5)
Marque el tipo de intersección( te fabricada reforzada,etc )
Marque las localizaciones de soporte en el isométrico ( cruces con acero asequibles, etc.)
¿Se considera la condición de prueba de carga hidráulica para tomar cargas de soportes estructurales?
Son necesarios los planos de tuberías de esfuerzos isométricos de tubería (ejes x, y, z) y cortes.
10.6
1.
2.
3.
4.
5.
6.
7.
8.
Ideas útiles en diseño de tuberías
Los movimientos máximos en na localización de ramal deben ser más bajos que el limite especificado. El ramal debiera
descansar con bastante flexibilidad para absorber el movimiento del cabezal.
En el análisis Nuclear, el ramal también necesita ser incluido con el cabezal, si la razón del momento de inercia / <
40, en otras palabras no se permite el desacople. Cheque el criterio de la compañía para la razón
que se va a usar.
Si el ramal es analizado separadamente, los movimiento del desacople debieran ser incluidos en el movimiento inicial (ó
impuesto) en el calculo del ramal.
El valor del modulo de elasticidad a la temperatura de operación puede ser usado en la tubería para calcular las cargas en el
equipo , tal y como por el estándar API 610 (referencia 7 en capitulo 7). Usando
resultara en cargas mas bajas,
es mas baja que
. La tubería es mas flexible cuando el valor de E es mas bajo.
a causa de que
La guía no debiera ser localizada tan cera el cambio de dirección; una pierna mínima debe ser requerida para absorber la
expansión. Calcular la pierna mínima por el método remarcado en el capitulo 1.
No se puede obtener crédito para el muelleo frio en el calculo de esfuerzo; solo se pueden reducir las cargas en el equipo
por el efecto del muelleo frio.
Proveer zapatas mas largas en soportes de tubería, cuando la deflexión axial sea grande.
Las guías de la Comisión de Regulación Nuclear se seguirán en el diseño.
Resultados
Los resultados comúnmente conocidos en la información de salida de un análisis asistido por computadora, consisten de lo siguiente:
157
1.
2.
3.
De la alimentación de datos: Coordenadas de los nodos ó puntos de datos, longitud, diámetro, grosor, radio de curvatura,
peso total de tubería, temperatura, coeficiente de expansión, modulo de elasticidad, presión, peso de válvulas, longitudes,
cargas de viento, localización y tipo de soportes.
Resultados: Deflexiones, rotaciones, fuerzas, momentos, SIF, esfuerzos de flexión resultantes, esfuerzo torsional, y
esfuerzos de expansión.
Los requerimientos para los diferentes códigos varían. El cumplimiento del ASME/ANSI B31.3 se discute a continuación.
(a)
(b)
(c)
(d)
(e)
El grosor de pared usado debiera ser más grande que el grosor mínimo requerido usando la ecuación 2.1.
La presión de entrad debiera ser mas baja que la presión permisible calculada usando la ecuacion 2.4
El esfuerzo de expansión
calculado usando la ecuacion 4.7 debiera ser menos que el rango de esfuerzo de
expansión de la ecuacion 4.1 ó 4.2.
El esfuerzo de expansión no incluye uno u otro, el peso ó la carga de presión, sino solo las cargas térmicas.
El esfuerzo aditivo no debiera exceder el esfuerzo caliente
= esfuerzo flexor resultante de, la carga del eso + el esfuerzo de presión longitudinal
:
=
4.
5.
Si el sistema de tubería esta sobre esforzado ó si las cargas en la boquilla del equipo son excesivas, entonces la
flexibilidad del sistema de tubería necesita ser incrementado como se discutió en los capítulos 1 y 5.
La deflexión real ( máxima considerando casos de diferentes cargas ) debiera ser mas baja que el claro de la camisa.
La relación de esfuerzo es la relación de los esfuerzos de código ( tabla 10.2 ) para esfuerzos permisibles, y debiera ser
menos que 1.
10.7
Modelado por computadora
Los diferentes programas de computadora sugieren de manera distinta el ingreso (código de entrada) de los diferentes componentes
de tubería que . Las descripciones de guías siguientes, las condiciones de un programa lógico, la codificación podía ser diferente en
una modelación de un programa de computación asistido.
1.
Movimientos de anclaje inicial, descritos mas tarde en detalle.
2.
Tipo de intersecciones (ver figuras 10.6 hasta 10.11)
Te reducción
Te fabricada
Te no reforzada
Te reforzada, refuerzo ó silleta
Weldolet
Sockolet
Sweepolet
Pipet
Latrolet
158
3.
4.
5.
6.
7.
8.
9.
10.
11.
12
13.
Te soldable enchufable
Codos, curvas, codos de gajos, elbolet, codo soldable enchufable, soporte sobre la curva, y codos bridados ( ver figuras 10.17
hasta 10.18 )
Reducciones concéntricas y excéntricas, reducciones injerto, y medios coples ( ver figuras 10.13 hasta 10.16 )
Muelleo frio, corte corto o corte largo ( ec 4.12 )
Cargas de viento ( referencia 6, capitulo 9 )
Válvulas, bridas, operadores de válvula, tapones Cap, bridas ciegas ( ver figuras 10.19 hasta 10.21 )
Anclaje relajado para una dirección especifica de la sujeccion, anclaje flexible, la inclusión de la tasa de muelleo en el
anclaje de boquillas (ecuación 7.3).
Juntas de expansión ( fuelle simple, de balancín, articulada(bisagra), universal ), calculo de empuje de presión (ec 5.4)
Soportes de una dirección.
Peso de aislamiento, peso del contenido, peso del refractario (ec 9.20)
trazado de la espira, coordenadas de los puntos de balanceo.
Tubería enchaquetada ( figura 9.11 )
10.8
Movimientos de anclaje inicial y movimientos de soportes
Los anclajes y soportes están movidos una cantidad calculada en el análisis para incluir:
1.
2.
3.
El movimiento debido al crecimiento térmico de las torres, intercambiadores de calor, bombas, turbinas,etc.
Asentamiento de edificio, asentamientos de tanque ( puede ocurrir cuando la tubería esta fría )
Anclaje sísmico y movimientos de soporte conocido como SAM.
Movimientos debido al crecimiento térmico
Recipientes verticales
La figura 10.3 muestra un recipiente con boquillas en diferentes orientaciones. El movimiento térmico calculado esta basado sobre la
temperatura media y la longitud de la sección del recipiente. No es inusual tener muchas temperaturas diferentes en diferentes
elevaciones.
El coeficiente térmico para las temperaturas es obtenido del apéndice A1, y se muestra en la tabla 10.4
Tabla 10.4 Coeficiente térmico ( para figura 10.3 )
Temperatura,°F
Pulgadas/ 100 pies
70
0.00
200
0.99
250
1.40
400
2.70
550
4.11
700
5.63
159
El material de recipiente es acero al carbón y el diámetro es 72 pulgadas.
Figura 10.3
Crecimiento térmico en el recipiente.
El crecimiento térmico en la boquilla A = 12 ( 0.099 ) + 14 ( 0.014 + 8 ( 0.027 ) + 6 ( 0.0411 ) + 4 ( 0.0563 )
= 1.002 pulg
El crecimiento en la boquilla B = 0.3148 + 3 ( 0.027 ) = 0.3958 pulg
El crecimiento radial horizontal en B =
( 0.027 = 0.081 pulg
El crecimiento en C = 0 pulg
El crecimiento vertical en el soporte D = 0.53 + 2.5 ( 0.0411 ) = 0.632 pulg
Los problemas de flexibilidad son mas severos cuando el recipiente esta caliente y la tubería esta fría; la diferencia de elevación entre
la boquilla A y el soporte D debiera ser mínima para evitar un gran crecimiento diferencial, y así evitar un soporte de muelleo.Si el
soporte esta construido desde el acero estructural (frio), un resorte en esta localización de soporte es necesaria. Cuando esta
soportada desde el recipiente, la carga en D es critica y el cuerpo del recipiente necesita revisarse para esfuerzos localesDesde la
localización del soporte D, la tubería de arriba crece hacia arriba, y la tubería de abajo crece hacia abajo. El primer soporte rigido ,
mostrado como E, debiera no ser localizado tan cerrado a la caída para absorber el crecimiento hacia abajo.
Intercambiadores de calor
La figura 10.4 muestra un intercambiador de calor. La cosa importante concerniente al intercambiador es el encuentro del soporte
base a la que esta anclado (A1), y el otro soporte que esta ranurado mostrado en la figura 10.5. La base con las ranuras le es
permisible deslizar a lo alrgo del eje del intercambiador ( dirección +x en la figura 10.4 ). La selección de cual de los dos soportes es
anclado podía estar basado en el crecimiento de la tubería de conexión; es necesario que el intercambiador crezca con la tubería.
160
En la figura 10.4 la temperatura de la coraza es de solo 40°F y la coraza se contrae en vez de expandirse; el coeficiente de expansión
es 6.07 pulg/pulg/°F
El crecimiento vertical en P = ( +63 ) (6.07 x 10 ) ( 40-70 ) = -0.0115 pulg
( El signo negativo muestra que la coraza se contrae hacia abajo, Δy = - 0.0115 pulg )
Figura 10.4
Figura 10.5
Elevación del intercambiador
Anclaje y soporte ranuarado para intercambiador de calor
El crecimiento horizontal en P = Δx = ( -11 ) (6.07 x 10 ) ( 40-70 ) = -0.002 pulg
( El signo menos es usado para 11 pulg, a causa de que P esta en el lado negativo de las x del anclaje A1 en el cual comienza
el crecimiento horizontal ).
Δx en Q = ( 108 ) (6.07 x 10 ) ( 40-70 ) = -0.0197 pulg
Δy en Q = ( 30 ) (6.07 x 10 ) ( 40-70 ) = -0.0055 pulg
Δx en movimiento en la dirección x.
Algunas veces dos intercambiadores son encimados uno sobre el otro ó muy cercanos uno a otro; la expansión entre los
intercambiadores es críticamente importante.
10.9
Modelado de elementos de tubería
El modelado de elementos de tubería descrito por las figuras 10.6 hasta 10.21 es de The Tennessee Valley authority ( referencia 1 )
Figura 10.6
SIF Modelada para un Latrolet de 45 °
161
El miembro A hasta B ( fig 10.6 ) esta modelado usando la misma sección transversal en la tubería que corre (cabezal) pero sin peso;
el miembro B hasta C esta modelado usando el mismo diámetro interno como la tubería del ramal, pero tiene dos veces el grosor de
pared pero sin peso. Un peso alzado debiera ser sumado en el punto B para la latrolet . El peso de cualquier agua o aislamiento será
incluido sobre la carta de sección transversal de la tubería.
Preparación del extremo Descripción del factor de intensificación de esfuerzo
SIF
Soldada a tope
Punto A ( todos los miembros conectantes ) *
Computado
Punto C ( ambos miembros conectantes ) *
General
.
.
h=
t
SIF =
t = grosor de pared nominal del cabezal
r = radio medio del cabezal
Punto B (ambos miembros conectantes ) *
1.0
* En el lado C del miembro ramal use el mas grande de los SIF calculados aquí y el SIF del cabezal. Esto se aplica también en los puntos C siguientes de
referencia.
Sweepolet
En la figura 10.7 el miembro A hasta B esta modelado usando la misma sección transversal como la del cabezal pero sin peso; el
miembro B hasta C esta modelado lo mismo como ramal incluyendo el peso por pie de tubería.
Figura 10.7
Preparación del extremo
Soldada a tope
General
SIF modelada para sweepolet
Descripción del factor de intensificación de esfuerzo
Punto A ( todos los miembros conectantes ) *
Para ≤ 0.5
= 0.8
(
SIF
Computado
)
≥1
Para > 0.5
= 0.4
(
)
≥ 1.5
El punto C ( ambos miembros conectantes ) *
Computado
Sockolet, Thredolet, Weldolet
El la figura 10.8 el miembro A hasta B esta modelado usando la misma sección transversal como el cabezal pero sin peso.
162
Figura 10.8
SIF modelada para sockolet, thredolet , y weldolet
El miembro B hasta C (fig 10.8) esta modelado usando el mismo diámetro interno como el ramal pero tiene dos veces el grosor de
pared pero sin peso. Un peso alzado debiera ser sumado en el punto B para el sockolet. El peso de cualquier agua o aislamiento será
incluido sobre la carta de sección transversal de la tubería.
Preparación del extremo Descripción del factor de intensificación de esfuerzo
SIF
Soldada a tope
Punto A ( todos los miembros conectantes ) *
Computado
Punto C ( ambos miembros conectantes ) *
General
.
.
h= t
SIF =
SIF ≥ 1
t = grosor de pared nominal del cabezal
r = radio medio del cabezal
Punto B (ambos miembros conectantes ) *
1
45° Ye Lateral, 45° reductora Ye lateral, 45 ° Ye soldada enchufada Lateral, 45 ° Ye roscada lateral.
Para yes soldadas a tope laterales, los miembros A hasta B , y B hasta D (fig 10.9) están modelados lo mismo que el cabezal
incluyendo el peso por pie de tubería, y el miembro B hasta C esta modelado lo mismo que el ramal incluyendo el peso por pie de
tubería.
Figura 10.9
SIF modelada para yes laterales a 45°
Para yes laterales soldadas enchufables, los miembros A hasta B , B hasta C , y B hasta D están modelados usando el mismo diámetro
nominal de tubería como la del cabezal, con accesorios clase cedula 80 para 3 000 psi, y accesorios cedula 160 usados para 6 000 psi
pero sin peso (referencia 2). Un peso alzado debiera ser sumado en el punto B para la Ye lateral. El peso de cualquier agua o
aislamiento será incluido sobre la carta de sección transversal de la tubería.
163
Preparación del extremo
Soldada a tope
General
Descripción del factor de intensificación de esfuerzo
Punto B
.
.
h=
t
SIF =
t = grosor de pared nominal del cabezal
r = radio medio del cabezal
θ= 45°
Los puntos A, C, y D ( lados laterales )
para t ≥ 0.322
t < 0.322
transición cónica de 30°
t = grosor nominal de pared
SIF
Computado
1.0
1.8
1.9
Copa soldable, medio cople soldable enchufable, medio cople roscado, couplet soldable
El miembro A hasta B ( fig 10.10 ) esta modelado usando la misma sección transversal como el cabezal pero sin peso. El miembro B
hasta C esta modelado usando el mismo diámetro nominal de tubería como el ramal, con accesorios clase cedula 80 para 3 000 psi, y
accesorios cedula 160 usados para 6 000 psi pero sin peso. Un peso alzado debiera ser sumado en el punto B para la copa soldable. El
peso de cualquier agua o aislamiento será incluido sobre la carta de sección transversal de la tubería.
Figura 10.10
Preparación del extremo
Soldada a tope
General
SIF modelada para couplet soldado.
Descripción del factor de intensificación de esfuerzo
Punto A ( todos los miembros conectantes ) *
Punto C ( ambos miembros conectantes ) *
½
SIF = 1.5
´
SIF ≥ 1
≤ 50
SIF
Computado
´
´
≤ 0.5
= radio medio del cabezal
´ = radio medio del ramal
= grosor de pared nominal del cabezal
= grosor de pared nominal del cabezal
= radio exterior del cople o copa.
Punto B (ambos miembros conectantes ) *
2.25
164
Te, te soldable enchufable, te reductora, te roscada
Para tés soldables a tope ( figura 10.11 ), los miembros A hasta B, y B hasta D están modelados lo m ismo como el cabezal incluyendo
el eso por pie de tubería, y el miembro B hasta C esta modelado lo mismo que el ramal. Para tes tipo soldable enchufable, los
miembros A hasta B, B hasta C, y B hasta D usan el mismo diámetro nominal de tubería como el ramal, con accesorios clase cedula 80
para 3 000 psi, y accesorios cedula 160 usados para 6 000 psi pero sin peso (referencia 2). Un peso alzado debiera ser sumado en el
punto B para la te. El peso de cualquier agua o aislamiento será incluido sobre la carta de sección transversal de la tubería.
Figura 10.11 SIF modelada para Te, te soldable enchufable, te reductora
Preparación del extremo
Soldada a tope
General
Enchufable
Soldado
Descripción del factor de intensificación de esfuerzo
Punto B
Puntos A, B, y D ( lado de TE )
para t ≥ 0.322
t < 0.322
transición cónica de 30°
t = grosor nominal de pared
Punto B
Puntos A, B, y D ( lado de TE )
SIF
Computado
1.0
1.8
1.9
Computado
1.0
Tubería Recta
El miembro A hasta B ( figura 10.12 ) tiene el peso de la tubería y el peso de cualquier agua o aislamiento será incluido
sobre la carta de sección transversal de la tubería. Ver las otras paginas para los factores de intensificación de esfuerzos debidos a
los accesorios en los ramales de la tubería.
Figura 10.12
SIF modelada para tubería recta.
165
Preparación del extremo
Soldada a tope
General
Brida loca ( para stub end )
Soldada enchufable
Roscada
Brida deslizable
Descripción del factor de intensificación de esfuerzo
Puntos A y B ( lados del miembro )
para t ≥ 0.322
t < 0.322
transición cónica de 30°
t = grosor nominal de pared de tubería
Puntos A y B
Puntos A y B
Puntos A y B
Puntos A y B
SIF
1.0
1.8
1.9
1.6
2.1
2.3
2.1
Reducción concéntrica
El miembro A hasta B ( figura 10.13 ) esta modelado lo mismo que el mas grande adicionado.
Figura 10.13 SIF modelada para reducción concéntrica
Preparación del extremo
Soldada a tope
General
Descripción del factor de intensificación de esfuerzo
Punto A ( lado de la reducción )
Punto B ( lado de la reducción )
SIF
2.0
computado
SIF =2
= modulo de sección de la tubería mas grande
= modulo de sección de la tubería mas pequeña
Reducción excéntrica
El miembro A hasta B ( figura 10.14 ) esta modelado lo mismo que la tubería mas grande incluyendo el peso por pie de tubería. El
desfase entre A y B esta modelado
Figura 10.14 SIF modelada para reducción excéntrica
166
Preparación del extremo
Soldada a tope
General
Descripción del factor de intensificación de esfuerzo
Punto A ( lado de la reducción )
.
SIF =
h = 4.4
Punto A ( lado de la reducción )
SIF =
.
h=
.
1
t
SIF
Computado
Computado
SIF ≥ 2
= radio medio de la tubería mas grande
= modulo de sección de la tubería mas grande
= modulo de sección de la tubería mas pequeña
Injerto reductor
El miembro A hasta B ( figura 10.15 ) esta modelado usando el mismo diámetro nominal de tubería como la tubería conectada en el
punto B pero sin peso: accesorios cedula 80 para 3 000 psi, y accesorios cedula 160 usados para 6 000 psi pero (referencia 2). Un
peso alzado debiera ser sumado en el punto A para el injerto. El peso de cualquier agua o aislamiento será incluido sobre la carta de
sección transversal de la tubería.
SIF = 2.25 ( el mismo que para extremo soldado enchufable )
Figura 10.15 SIF modelada para injerto reductor
Cople, cople roscado, cople reductor soldado enchufable
El miembro A hasta B ( figura 10.16 ) esta modelado usando el mismo diámetro nominal como la tubería acoplada ( el mas grande
diámetro nominal, si es un cople reductor ) con accesorios clase cedula 80 para 3 000 psi, y accesorios cedula 160 usados para 6 000
psi pero sin peso (referencia 2). Un peso alzado debiera ser sumado en lo puntos A y B para el cople. El peso de cualquier agua o
aislamiento será incluido sobre la carta de sección transversal de la tubería.
SIF = 2.25 ( el mismo que para extremo soldado enchufable )
167
Figura 10.16
SIF modelada para cople
Todos los codos
Para codos soldados a tope ( figura 10.17 ) el miembro A hasta C esta modelado como a la tubería que se une incluyendo el peso por
pie de tubería. Un retorno de 180° se modela como dos codos de 90°. Si es un codo reductor, el miembro A hasta C es modelado lo
mismo que el tubo adicionado más grande.
Para codos soldados enchufables, los miembros A hasta B y B hasta C están modelados como miembros rectos usando el mismo
diámetro nominal como la tubería acoplada con accesorios clase cedula 80 para 3 000 psi, y accesorios cedula 160 usados para 6 000
psi pero sin peso (referencia 2). Un peso alzado debiera ser sumado en el punto B para el codo. El peso de cualquier agua o
aislamiento será incluido sobre la carta de sección transversal de la tubería.
Figura 10.17 SIF modelada para codos
Elbolet ( soldado enchufable, soldado a tope, roscado )
El miembro A hasta C ( figura 10.18 ) esta modelado usando la misma sección transversal como el cabezal pero sin peso. El miembro
C hasta D esta modelado usando el mismo diámetro nominal como el ramal pero tiene dos veces el grosor de pared pero sin peso.
Un peso alzado debiera ser sumado en el punto B para el elbolet. El peso de cualquier agua o aislamiento será incluido sobre la carta
de sección transversal de la tubería.
168
Figura 10.18
Preparación del extremo
Soldada a tope
General
SIF modelada para elbolet
Descripción del factor de intensificación de esfuerzo
Punto A ( miembro A hasta B ) lo mismo como el codo
SIF
Punto A ( miembro A hasta C ) y punto C ambos miembros
conectados
Punto D (ambos miembros conectados )
.
=
≥1
1.0
=
.
≥1
SIF =
Computado
x
=
=
t = grosor de pared nominal del cabezal
r = radio medio del cabezal
R = radio de curvatura del codo
Válvulas, Válvulas con operador
En la figura 10.19, los miembros A hasta B, B hasta C , y B hasta D ( si existe el operador )son modelados usando el mismo diámetro
interno como la tubería acoplada pero con el doble de pared sin peso. Los miembros A hasta B y B hasta C tienen el peso de cualquier
agua o aislamiento de la carta de sección transversal de tubería. Los pesos alzados de la válvula y el operador ( si existe el operador )
debieran ser sumadas a los puntos donde se necesiten. Se requieren los dos puntos de masa, uno para la válvula y uno para el
operador CG.
Figura 10.19 SIF modelado para válvulas sin operador
169
Todas las Bridas
Los miembros A hasta B Y B hasta C ( figura 10.20 ) están modelados usando el mismo diámetro interno como la tubería acoplada
pero con el doble de pared sin peso. Un peso alzado debiera ser sumado en B para las bridas. El peso de cualquier agua o aislamiento
será sobre la carta de sección transversal de la tubería.
Figura 10.20 SIF modelada para bridas
Tapón Capa.
El miembro A hasta B ( figura 10.21 ) esta modelado usando las mismas secciones transversales como para el Cap. El peso de
cualquier agua o aislamiento será incluido en la carta de sección transversal de la tubería.
Referencias
1.
2.
Tennessee Valley Authority, Piping Analysis Procedure.
Oakridge National Laboratory Report ORNL - TM - 4929
170
APENDICES
171
Tablas A1.1
Expansion térmica Total
172
Tabla A1.2
Expansión térmica Total
173
Tabla A1.3
Expansión térmica Total
174
Tabla A1.4
Expansión térmica Total
175
Tabla A1.5
Expansión térmica Total
176
Tabla A1.6
Expansión térmica Total
177
Tabla A1.7
Expansión térmica Total
178
Tabla A1.8
Expansión térmica Total
179
Tabla A1.9
Expansión térmica Total
180
Tabla A1.10
181
Tabla A2 . 1
Módulos de elasticidad
182
Tabla A2 . 2
Módulos de elasticidad
183
Tabla A2 . 3
Módulos de elasticidad
184
Tabla A2 . 4
Módulos de elasticidad
185
186
187
Tabla A3 . 1
Esfuerzos permisibles
188
Tabla A3 . 2
Esfuerzos permisibles
189
Tabla A3 . 3
Esfuerzos permisibles
190
Tabla A3 . 4
Esfuerzos permisibles
191
Tabla A3 . 5
Esfuerzos permisibles
192
Tabla A3 . 6
Esfuerzos permisibles
193
Tabla A3 . 7
Esfuerzos permisibles
194
Tabla A3 . 8
Esfuerzos permisibles
195
Tabla A3 . 9
Esfuerzos permisibles
196
Tabla A3 . 10 Esfuerzos permisibles
197
Tabla A3 . 11 Esfuerzos permisibles
198
Tabla A3 . 12 Esfuerzos permisibles
199
Tabla A4. 1
Propiedades y pesos de tubería
200
Tabla A4. 2
Propiedades y pesos de tubería
201
Tabla A4. 3
Propiedades y pesos de tubería
202
Tabla A4. 4
Propiedades y pesos de tubería
203
Tabla A4. 4
Propiedades y pesos de tubería
204
Problemas diversos
Calculos muestra para refuerzos de ramales
Desgraciadamente se encuentra desaparecido la primera parte del ejemplo 1
X
X
X
X
X
205
Ejemplo 2
Hay un ramal de 8”Ø en ángulo recto a un cabezal de 18”Ø ( Fig A1 ); ambos cabezal y ramal son tubería sin costura ced 80 ASTM
A335 grado P11. La conexión esta reforzada con un anillo de 14”de diámetro exterior ( medido a lo largo del cabezal), se cortó una
pieza de un tubo sin costura de 18ӯ ced 80 ASTM A335 grado P12 y se coloco el ramal. La costura de soldadura tiene las
dimensiones mínimas. Se especificó una corrosión permisible de 0.10 pulg .¿ Cual es la presión de operación normal máxima
permisible, si la temperatura de operación normal es de 1 005°F ?
Solucion:
Del apéndice A tabla 1 del B31.3 ( apéndice A3 ) SE = 7.68 ksi para grado P11, y SE = 7.38 ksi para grado P12, ambos a
1 005 °F.
Dimensiones de pierna de soldaduras: ( ver fig A1 para dimensiones de soldadura )
=
.
.
.
.
.
.
= 0.354 pulg
( debido a 0.25 pulg de soldadura minima )
= 0.663 pulg
= ( 0.938 ) ( 0.875 ) = 0.821 pulg
= ( 0.5 ) ( 0.875 ) = 0.438 pulg
= ( 0.938 ) ( 0.875 ) = 0.821 pulg
( debido a M T de 12.5% )
= 2.5 ( 0.438 - 0.1 )+ 0.821 = 1.666 pulg
[ Este es mas pequeño que 2.5 ( 0.821 - 0.1 ) = 1.8 pulg ]
= = 8.625 - 2( 0.438 -0.1 ) = 7.949 pulg
Coeficiente y para 1 005°F = 0.7 ( tabla 2.1 )
SE = 7.68 ( apéndice A3 )
=
=
.
.
Usando la ecuacion q =
= 18 q y
(2.1)
.
.
.
, nosotros podemos escribir brevemente
= 8.625 q
206
= 143.08 q
El área requerida, = 7.949
El area de refuerzo
=(7.949)(0.821 - 18q -0.1 ) = 5.731 - 143.08q
en la pared del cabezal,
= (2)(1.666)(0.438 - 8.625q- 0.1 ) = 1.126 - 28.73q
en la pared del ramal,
=(0.821)(14-8.625)(7250/7570) = 4.226
en el anillo refuerzo,
= (2)(0.5) 0.354 + (2)(0.5) 0.663 = 0.565
en la costura de soldadura,
El area total de refuerzo
= 11.648- 171.818 q
(2.10)
(2.12)
(2.13)
En la presión de operación normal máxima permisible, el área requerida y el área de refuerzo son iguales; por lo tanto:
143.08 q = 11.648 - 171.818 q ; 314.898 q = 11.648 ;
Pero también,
q=
En estos términos,
.
q = 0.037
.
P = ( 0.037 ) ( 15360 + 1.4 P ) = 568.32 + 0.0518 P
0.948 P = 568.32
P = 699.494 psig la cual es la presión de operación normal máxima permisible.
Ejemplo 3
En un sistema de tuberías de aceite un ramal de 6”Ø ced 40 tiene su eje a un ángulo de 60° , con respecto al cabezal de 16”Ø ced
40 ( fig A1 ). Ambas tuberías son sin costura API 5L grado A. La conexión esta reforzada con un anillo de 12” de diámetro exterior
(medido a lo largo del cabezal) hecho de placa ASTM A285 grado C. ------------ faltan datos que no se encuentran en el original
-------Tolerancia de corrosión = 0.10 pulg.
La presión de diseño es 500 psig a 700°F.
¿ Es adecuado el diseño para la presión interna ?
Solucion:
el
Los valores de esfuerzos permisibles del apéndice A tabla 1 del B31.3 ( apéndice A3 ) son: para el tubo, SE = 14.4 ksi; para
anillo, SE = 14.4 ksi
= ( 0.5 ) ( 0.875 ) = 0.438 pulg
= ( 0.28 ) ( 0.875 ) = 0.245 pulg
= 0.5 pulg
= 2.5 ( 0.0245 - 0.1 )+ 0.5
207
= 0.8625. Este es mas grande que 2.5 ( 0.438 - 0.1 ) = 0.845 pulg
=
.
=
=
= 0.274 pulg
.
= 0.113 pulg
.
=
.
El area requerida,
.
.
°
= 7.315 pulg
.
= ( 0.274 ) ( 7.315 ) ( 2- 0.866 ) = 2.27
El area de refuerzo
en la pared del cabezal,
en la pared del ramal,
en el anillo,
.
=
= ( 7.315 ) ( 0.438 - 0.274 - 0.1 ) = 0.468
= (2)
= 0.5 ( 12 -
en la costura de soldadura,
.
.
.
( 0.245 - 0.113 - 0.1 ) = 0.062
.
)
= 2.175
=(4)(½)
= 0.281
Area total de refuerzo
Este total es mas grande que 2.27
(2.10)
(2.12)
(2.13)
= 2.986
, por eso ningún refuerzo adicional se necesita.
Ejemplo 4
En un sistema de tubería de aceite se tiene un cabezal de 8”Ø y un ramal de 4”Ø en angulo recto ( fig A1 ). Ambas tuberías son sin
costura ced 40 API 5L grado A. Las condiciones de diseño son 350 psig a 400°F. Se asume que el sistema de tubería esta para
permanecer en servicio hasta que todo el grosor de metal, en ambos cabezal y ramal, en exceso del que es requerido por la ecuacion
2.1 se lo halla llevado la corrosión. ¿ Que refuerzo es requerido para esta conexión ?
Solucion:
El valor de esfuerzo permisible del apéndice A, tabla 1 del B31.3 ( apéndice A3 ) es SE = 16 ksi
=
.
.
= 0.0935 pulg
208
.
=
= 0.0448 pulg
.
= 4.5 - ( 2 ) ( 0.0448 ) = 4.402 pulg
El area de refuerzo requerida,
= ( 0.0925) ( 4.402 ) = 0.412
Tratar soldadura de filete solo.
= ( 2.5 ) ( 0.0935 ) = 0.234 pulg ó
= (2.5 ) ( 0.0488 ) = 0.122 pulg
usar 0.122 pulg
Debido a la limitación en la altura de la zona de refuerzo, ningún tamaño de soldadura de filete practica suministrará
suficiente área de refuerzo; por lo tanto, la conexión debe ser reforzada con un anillo. Tratar con un anillo de 6.5 pulg de DE
(diámetro exterior)(medido a lo largo del cabezal). Asumir que el refuerzo se cortara de una pieza de tubo sin costura de
8”Ø ced 40 API 5L grado A , y soldado posteriormente a la conexión con el tamaño mínimo de soldadura de filete.
Grosor mínimo de refuerzo, = ( 0.322 ) ( 0.875 ) = 0.282 pulg
= ( 2.5 ) ( 0.0488 ) + 0.282 = 0.404 pulg
Nueva
Ó
= ( 2.5 ) ( 0.0935 )
= 0.234 pulg
se usará 0.234 pulg
El área de refuerzo en el anillo ( considerando solo el grosor dentro de
= 0.234 ( 6.25 - 4.5 ) = 0.41
Dimensión del pie de soldadura :
= 0.228 pulg
):
Área de refuerzo en la soladura de filete:
= ( 2 ) ( ) 0.228 = 0.052
Área total de refuerzo,
=
+
= 0.462
Esta área total de refuerzo es mas grande que el área de refuerzo requerida, por eso, un anillo de refuerzo de 6.25 “ de DE,
cortado de una pieza de tubo sin costura de 8” Ø ced 40 API 5 L grado A y soldado a la conexión ramal con una soldadura
de filete mínima proveerá adecuado refuerzo para la conexión.
209
Ejemplo 5 ( no ilustrado )
Un cople soldado enchufable de acero forjado de 1½”Ø de 3 000 # ( rango de presión ) se soldó en ángulo recto a una pieza de tubo
sin costura de 8”Ø ced 40 ASTM A53 grado B, para un servicio de aceite. La presión de diseño es 400 psi y la temperatura de diseño
es 450°F. La corrosión permisible es 0.1 pulg. ¿ Se requiere refuerzo adicional ?
Solución
No, dado que el ramal es menor que 2”Ø(de acuerdo al código B 31.3, sección 304.3.2 (b) ), el diseño es adecuado para
sostener la presión interna y ningún calculo es necesario. Se presume, por supuesto, que los cálculos han mostrado que el
cabezal ha satisfecho las condiciones de servicio de acuerdo a las ecuaciones 2.1, 2.3, y 2.4 .
210
INDICE
Abrazadera ( brace )
13
Aceleración
34, 117
Acero al carbón
172, 173,181
Acero Austenitico
9,171
Acero de aleación intermedia
7,9,46,71,190
Aislamiento
8,36
Aislamiento reflectivo
36
Aislamiento tipo masa
36
Aleaciones no ferrosas
125,181
Amortiguador
13
Análisis formal
47
Anillo
31
Anclaje direccional
81
Anclaje intermedio
82
Anclaje ( movimiento )
4,187
Anclaje principal
82
Angulo de conicidad
149
Área de metal
12,199
ANSI ( código )
44
ASME Sección III ( código )
44,147
ASTM ( estándares )
7
B 31.1 ( código )
62,117
B 31.3 ( código )
47
B 31.4 ( código )
127
B 31.8 ( código )
44
Bijlard ( curvas de )
95,96
Bomba centrifuga
110
Brida de cara realzada
11,90
Brida de cuello soldable
10,52
Brida de enchufable soldable
7,160
Brida deslizable
12,81
Bronce
173
Cabezal
31,49
Caída de presión
11
Calificación
157
Calculo de claro
33,39
Calculo simplificado cantiléver guiado
14
Calculo simplificado de esquina cuadrada 16
Calculo simplificado de espira
16
Calculo simplificado de perfil “L”
16,17,19
Calculo simplificado de perfil “Z”
16,18,19
Calculo simplificado método Kellog 16,19
Calculo simplificado de tube turns 17,20
Cantilever
14,15
Capa ( tapón )
169
Características de flexibilidad 51,60,148
Carga
Carga auto limitante
8
Carga del peso
Carga de bombeo
110
Carga de nieve
8
Carga de presión
8,45
Carga estática
8,91
Carga muerta
8,152,153
Carga permisible
108
Carga primaria
8
Carga secundaria
8,147,153
Carga sobre tubería
8
Carga sostenida
8,153
Carga viva
8
Cargas de boquilla
106
Cargas de diseño
147
Cargas de equipo
96,106
Cargas de gravedad
8,152
Carga de viento
8,42,44
Cargas dinámicas
8,91,147
Cargas ocasionales
153
Cargas sísmicas
8,41
Choque Jet ( Jet impingement)
153
Ciclos
45,47,147
Circulo de tornillos
90
Claro critico
33
Claro para tubería nuclear
42
Claro permisible
33
Clase 2 ( NC ) ( tubería )
153
Clase 3 ( ND ) ( tubería )
147
Código de plantas químicas
47
Código de recipientes a presion
44,135
Código de transporte de gas
44
Código de transporte de líquidos
127
Código nuclear
44,147
Código de refinerías
47
211
Calculo simplificado método Grinell
15,19
Código de tuberías de potencia
117
Codos
51,148,167
Codo bridado
52,149
Codo de gajos
25,26,28,51,55,148
Codo de gajos amplios
26,51
Codo de gajos cerrados
51
Codo de gajos simples
26,51
Codo de múltiples gajos
26
Codo de radio largo
54
Coeficiente de carga
128
Coeficiente de expansión
8,9,12,171
Coeficiente de fricción
127
Colgante
13
Colgante de rodete
13
Combeo ( bowing )
126
Componentes de presión
21
Composición química
7,8
Compresor centrifugo
110
Condición cíclica
6
Condición de emergencia
153
Condición de falla
93
Condición final
33
Condición normal
153
Condición recalcada
93,153
Construcción del reactor
37
Contracción
8
Copa soldada
149,163
Cople
163
Cople Dresser
81
Cople Victaulic
81
Corrosión permisible
8,19,26
Couplet
163
Cuerpo esférico
99
Curvas
12,49,51,148,167
Deflexión
33
Deflexión permisible
34
Deformación
5
Densidad
9,18
Desfase, desacople ( mismatch )
149
Desfase, corrimiento ( offset )
12
Diámetro
199
Diámetro exterior ( OD )
199
Diámetro interior ( ID )
199
Diseño base accidente
153
Diseño con presión externa
116,131
Dispositivo de amortiguación
13
Distorsión
44
Drenaje
36
Ecuación Lame
24
Ecuación NEMA
108
Ecuación de Markl
50
Efecto de deslizamiento longitudinal
116,141
Efecto de torsión (TWISTING)
5
Efecto del peso
8,147
Efecto flexor
15
Efecto térmico
5,8
EJMA
81
Elbolet
167
Empaque
11,91,93
Empuje de válvula
152
Empuje de válvula de alivio de presión
116,119
Equipo rotativo
106
Esfuerzo
5,63
Esfuerzo caliente
39,45
Esfuerzo de anillo
128,153
Esfuerzo de cedencia
5,46,102,185
Esfuerzo de código
63,153
Esfuerzos de flexibilidad
63
Esfuerzo de presión
151
Esfuerzo flexor
15,17,63,64,126
Esfuerzo local
96
Esfuerzos locales de recipientes
96,97
Esfuerzo longitudinal
45,127
Esfuerzo permisible
6,44,153
212
Esfuerzo radial
128
Esfuerzo tensor
185
Esfuerzo torsional
13
Espaciado ( gap )
73
Espaciado para soportes
39
Espacio de gajos
56
Especificación
10,11
Espira
12,60,72-78
Espira de expansión
12,72
Expansión
8,171
Expansión térmica
171
EZFLEX ( programa de computo )
16
Factor de calidad de fundición
22
Factor de calidad de junta
22
Factor de calidad
22,26
Factor de carga dinámica
120
Factor de concentración de esfuerzo
98
Factor de intensificación de esfuerzo
50,148
Factor de corrección de SIF
59
Factor de flexibilidad
51,52,148
Factor de junta soldada
22
Factor de reducción de claro
34
Factor de reducción de esfuerzo
46
Factor de seguridad
5,6
Falla
5,6
Fatiga
10,44,45
Flexibilidad
10,11,12
Flujo de fluido
20
Frecuencia natural
33,120,154
Fricción de flujo
7
Fuelles
12,81,153
Fuelles metálicos
82
Fuerza
5
Fuerza de empuje
85,128
Fuerza de empuje de presión
85,153
Fuerza de impacto
8
Fuerza térmica
12,19
Fuerza ultima
5
Fuga en brida
10
Golpe de agua
152
Gravedad especifica
9,39
Gradiente promedio
36
Grosor
21,199
Grosor de presión de diseño
21,28
Grosor de la bifurcación (crotch)
52
Grosor de pared
8,21,24,199
Grosor mínimo
21
Guía
42,73
Hastelloy
8,125
Hook ( ley de )
5
Incoloy
125
Inconnel
8,125
Injerto
166
Interferencia
73
Interpolación
27
Juntas de bola
81
Juntas empacadas
81
Junta bridada
52,90
Junta de expansión
12,72,81,83,84,87,88,153
Junta de soldadura de filete
52
Junta deslizante
81
Junta flexible
81
Juntas giratorias
13
Ladeo ( sway )
34
Latrolet
160,162
Limite proporcional
5,6
LOCA
91
Manguera
81
Manguera metálica
81,87
Materiales dúctiles
5,173
Materiales para tubería
6,7
Material de fierro fundido
5,173
Material ferroso
181
Método de Cantilever guiado
14
213
Método de esquina cuadrada
Método Grinell
Método ITT Grinnell
Método M W Kellogg
Método Tube Turns
Modo
Modulo caliente
Modulo de elasticidad
Modulo de sección
Modulo de sección para ramal
Modulo de Young
Modulo frio
Momento
Momento externo
Momento de inercia
Momento flexor en plano
Momento flexor fuera de plano
Momento permisible
Monel
Movimiento de anclaje
Movimiento de anclaje sísmico
Movimiento de presión contenida
Movimientos extraños
Muelleo frio
Nomografica para espiras
Numero de cedula
Operación base terremoto
Operadores de válvula
Orificio
Orillas achaflanadas
Pandeo ( sag )
Paro(bumper)
Paro limite
Pendiente para drenaje
Periodo de instalación de válvula
Peso contenido
14
15,20
15,20
16,76,79,80
17,20
154
10,34
5,9,181
15,16,199
64
5,9,18
15
5
91
16,199
49
49
91, 93
202
8,158
153
153
45,158
66,153
78
199
91,152
158,168
11
11
36
13
13
36
120
9,34,37,199
Peso de agua
Peso de aislamiento
Peso de metal
Peso especifico
Precarga
Precarga de tornillos
Presión atmosférica
Presión de diseño
Presión de prueba
Presión de prueba hidrostática
Presión de trabajo permisible
Presión externa
Presión interna
Pulsación
Radio de giro
Ramal reforzado
Rango de esfuerzo
Rango de esfuerzos permisibles
Rango de presión de bridas
Reacción fría
Reactor
Recipientes cilíndricos
Reducción
Refuerzo ( pad )
Refuerzo de recipientes
Refuerzo
Relación (razón ) de Poisson
Relajación de esfuerzo
Relleno ( back fill )
Resistencia de fricción
Resonancia
Resultados
Revisión de gradiente
Rigidez
Rigidez de boquilla
Ruptura
199
34,37
34,199
9
153
90
118
25
25,86
25,85
24
8,90,131
8,44,90
34,145
119
51
15,46
15,45
11,94
68,69
147
98,100,137
149,152,165
28,52,57
97
27,204
9,18
141
127
129
34
157
36
15
102
153
214
Ruptura de tubería
153
Sepultada ( tubería )
132,144
SIF en plano
51
SIF fuera de plano
51
Silleta
31,52
Sistema de descarga abierta
136
Sockolet
161
Soporte de descanso
13
Soporte de esfuerzo constante
13
Soporte de muelle
13
Soporte de zapata
12
Soporte elastico
13
Soporte rígido
13
Soportes
8,33,117
SRSS
153
Stub in ( injerto )
51
Sujeción
13
Sweepolet
161
Tapa ciega ( grosor )
25
Tasa de muelleo
13
Tasa de muelleo para boquilla
102
Te
11,50,51,57,164
Te enchufable soldable
57,113
Temperatura
90
Te extruida
51
Te reducción
164
Te reforzada
51,148
Te soldada enchufable
194
Temperatura de instalación
8
Tensión
5
Teoría de la máxima deformación
127
Terremoto
8,147
Terremoto de paro de seguridad
102,182
Threadolet
11
Thredolet
192
Tirón de desplazamiento
44
Titanio
125
Tolerancia
Tolerancia de corrosión
Tolerancia de manufactura
Tolerancia de laminación
Torcimiento ( squirm )
Trinchera
Tubería cargada uniformemente
Tubería corrugada
Tubería de acero inoxidable
Tubería de agujero pequeño
Tubería de alta energía
Tubería de acero aleada
Tubería de acero al carbón
Tubería de aleación de aluminio
Tubería de aleación de cobre
Tubería de aleación de níquel
Tubería de fundido centrifugado
Tubería de gas
Tubería de pared delgada
Tubería de pared gruesa
Tubería enchaquetada
Tubería plástica
Tubería sin costura
Tubería subterránea
Tubos
Turbina de vapor
Unidades métricas
Vapor
Válvulas
Válvulas activas
Válvulas de alivio
Válvula de compuerta
Válvula de globo
Válvula de retención
Varilla de tensión ( tierod )
Viga
Viga soportada simplemente
21
4,7,28
21,26
32
82
126
33
15,52,81,149
7,10,38,46
16
50
7
6,7,172,173,185
7,38,116,122,175
7,116,123
7,116,171
191
44
24,52
24
8,116,138
116
7,11,185
116,126
185
106
116,140
118
8,10,11116,168
117, 153
43,117
11,116
10
11
83
154
33
215
Weldolet
WRC (boletín)
Zirconio
Zona de refuerzo
11,32,51,57,161
96
8,125
28
216
Anexos.
Problemas resueltos.
Capitulo 1:
1.
(a) Hallar la expansión total para una tubería de acero de aleación intermedia ( 5Cr Mo a 9 Cr Mo ) a
temperaturas de (1) -55°F, (2) 431 °F, (3) 1572 °F. Si la temperatura dada esta fuera del rango del
material, sugerir un material apropiado para esa temperatura. Considerar una longitud de 120 pies.
Respuesta:
1)
Coeficiente para -50°F = 0.79 pulg/100 pies
Coeficiente para -75°F = 0.94 pulg/100 pies
Diferencia por grado de expansión = (0.94 - 0.79) / 25 = 0.006
Por interpolación, la expansión para -55°F = -0.79 + [ (-55)-(-50) ]0.006 = -0.79 +(-0.03) =
= -0.79 - 0.03 = 0.82 pulg/100 pies
2)
/
} = 0.082 pies
Coeficiente para 425°F = 2.72 pulg/100 pies
Coeficiente para 450°F = 2.93 pulg/100 pies
Diferencia por grado de expansión = (2.93 - 2.72) / 25 = 0.0084
Por interpolación, la expansión para 431°F = 2.72 + [ 431 - 425 ]0.0084 = 2.72 +(0.0504) =
= 2.72 + 0.0504 = 2.77 pulg/100 pies
La expansión térmica total para 120 pies ={
3)
.
x
La contracción térmica total para 120 pies ={
x
.
/
} = 0.277 pies
Coeficiente para 425°F = 2.72 pulg/100 pies
Coeficiente para 450°F = 2.93 pulg/100 pies
Diferencia por grado de expansión = (2.93 - 2.72) / 25 = 0.0084
Por interpolación, la expansión para 431°F = 2.72 + [ 431 - 425 ]0.0084 = 2.72 +(0.0504) =
= 2.72 + 0.0504 = 2.77 pulg/100 pies
La expansión térmica total para 120 pies ={
(b)
x
.
/
} = 0.277 pies
Hallar los siguientes datos para aceros austeniticos a la temperatura de operación:
1.
Modulo de Young.
2.
Razón de Poisson.
3.
Densidad.
217
(c)
Calcular la elongación total en 132 pies de tubería hecha de acero al carbón sujeta a 645 °F.
218