Institución Educativa María Montessori Docente: Gloria Pacheco

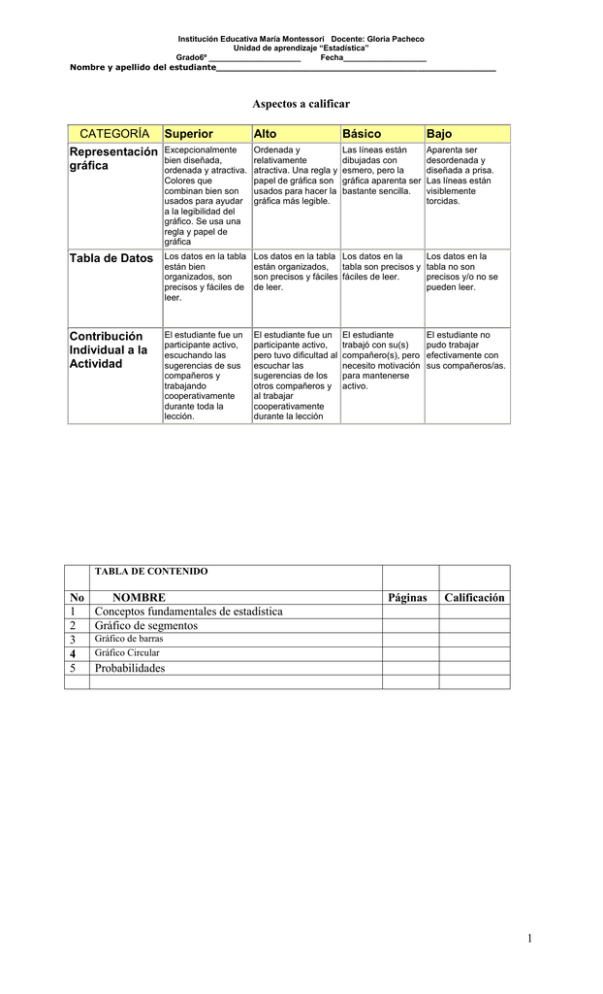
Institución Educativa María Montessori Docente: Gloria Pacheco
Unidad de aprendizaje “Estadística”
Grado6º _____________________
Fecha___________________
Nombre y apellido del estudiante__________________________________________________
Aspectos a calificar
CATEGORÍA
Superior
Alto
Básico
Bajo
Representación
gráfica
Excepcionalmente
bien diseñada,
ordenada y atractiva.
Colores que
combinan bien son
usados para ayudar
a la legibilidad del
gráfico. Se usa una
regla y papel de
gráfica
Ordenada y
relativamente
atractiva. Una regla y
papel de gráfica son
usados para hacer la
gráfica más legible.
Las líneas están
dibujadas con
esmero, pero la
gráfica aparenta ser
bastante sencilla.
Aparenta ser
desordenada y
diseñada a prisa.
Las líneas están
visiblemente
torcidas.
Tabla de Datos
Los datos en la tabla
están bien
organizados, son
precisos y fáciles de
leer.
Los datos en la tabla Los datos en la
están organizados,
tabla son precisos y
son precisos y fáciles fáciles de leer.
de leer.
Los datos en la
tabla no son
precisos y/o no se
pueden leer.
Contribución
Individual a la
Actividad
El estudiante fue un
participante activo,
escuchando las
sugerencias de sus
compañeros y
trabajando
cooperativamente
durante toda la
lección.
El estudiante fue un
participante activo,
pero tuvo dificultad al
escuchar las
sugerencias de los
otros compañeros y
al trabajar
cooperativamente
durante la lección
El estudiante no
pudo trabajar
efectivamente con
sus compañeros/as.
El estudiante
trabajó con su(s)
compañero(s), pero
necesito motivación
para mantenerse
activo.
TABLA DE CONTENIDO
No
1
2
3
4
5
NOMBRE
Conceptos fundamentales de estadística
Gráfico de segmentos
Páginas
Calificación
Gráfico de barras
Gráfico Circular
Probabilidades
1
Institución Educativa María Montessori Docente: Gloria Pacheco
Unidad de aprendizaje “Estadística”
Grado6º _____________________
Fecha___________________
Nombre y apellido del estudiante__________________________________________________
Reflexión: “Dios revela lo profundo y lo
tinieblas, y con Él mora la luz”.
escondido; conoce lo que está en
Daniel 2:22
Tema: ESTADÍSTICA
Objetivo:
 Reconocer algunos conceptos fundamentales de la estadística
 Realizar tablas de frecuencias para datos no agrupados
Materiales: Recortes de periódicos y revistas que muestren datos estadísticos
Conceptos:
CONCEPTOS FUNDAMENTALES DE ESTADÍSTICA
ESTADÍSTICA.
La estadística está ligada con los métodos científicos en la toma, organización, recopilación, presentación
y análisis de datos, tanto para la deducción de conclusiones como para tomar decisiones razonables de
acuerdo con tales análisis.
En un sentido más estricto, el término se utiliza para denotar los mismos datos o números que se derivan
de ellos, como, por ejemplo, promedios. Así se habla de estadística de empleo, estadística de accidentes
etc.
Actividad: De un periódico recorte datos que representen estadísticas
POBLACIÓN
Una población es un conjunto de todos los elementos que estamos estudiando, acerca de los cuales
intentamos sacar conclusiones.
Ejemplo 1. Estudiantes de la I.E. María Montessori
Ejemplo 2. Habitantes de la comuna 5 de la ciudad de Medellín
MUESTRA.
Se llama muestra a una parte de la población a estudiar que sirve para representarla
Ejemplo 1. Estudiantes grado sexto de la I.E. María Montessori
Ejemplo 2. Habitantes del barrio Francisco A. Zea de la comuna 5 de la ciudad de Medellín
Actividad: Escriba 5 ejemplos de población y de muestras de las mismas.
ESTADÍSTICA CUALITATIVA Y CUANTITATIVA
ESTADÍSTICA CUALITATIVA: Cuando los datos suministrados en una encuesta son cualidades o
atributos. Ejemplo: Color preferido, Música favorita, Programa de TV más visto
ESTADÍSTICA CUANTITATIVA: Cuando los datos suministrados en una encuesta son numéricos.
Ejemplos: Edad, Peso, Estatura
Actividad: Clasifica las siguientes variables en cualitativas o cuantitativas: Número de hermanos, color
de los ojos, Comida Favorita, Nº del calzado
Gep/15
2
Institución Educativa María Montessori Docente: Gloria Pacheco
Unidad de aprendizaje “Estadística”
Grado6º _____________________
Fecha___________________
Nombre y apellido del estudiante__________________________________________________
Reflexión: ¡CUAN PRECIOSA, OH DIOS, ES TU MISERICORDIA!
POR ESO LOS HIJOS DE LOS HOMBRES SE AMPARAN BAJO TUS ALAS
Salmo 36:7
Tema: GRÁFICOS ESTADÍSTICOS: Gráfico de Líneas
Objetivo:
 Reconocer el gráfico de líneas
 Realizar gráficos de líneas
Conocimientos previos: Tabla de frecuencias
Materiales: Escuadras, lápiz
Conceptos:
GRÁFICOS ESTADÍSTICOS: Los gráficos estadísticos son formas vistosas de presentar los
resultados organizados en las tablas de frecuencias.
Existen muchos tipos de gráficos Hoy estudiaremos el gráfico de líneas, para ello tomaremos
como referencia la tabla de datos correspondiente a los programas de TV. favoritos de 75 niños
con edades entre 3 y 7 años:
Hi-Fi
Chica Supersabia
Dino Dan
Los Imaginadores
Mecanimales
10
15
20
5
25
GRÁFICO DE LÍNEAS: En este gráfico se representa con un punto la intersección entre la
variable estudiada en este caso, el programa preferido que se ubica en el eje X con su
frecuencia que se representa en el eje Y que en este caso es la frecuencia absoluta. Luego se
unen los puntos por medio de líneas.
N° de niños
50
PROGRAMAS PREFERIDOS
POR 75 NIÑOS ENTRE 3 Y 7
AÑOS
0
Programa Favorito
Se puede observar en el gráfico que el programa que más le gusta a los niños es Los
Mecanimales y el que menos gusta son los Imaginadores
Actividad:
1. Realizar una pregunta de investigación, construir la tabla de frecuencias y el
gráfico de líneas
Gep/15
3
Institución Educativa María Montessori Docente: Gloria Pacheco
Unidad de aprendizaje “Estadística”
Grado6º _____________________
Fecha___________________
Nombre y apellido del estudiante__________________________________________________
Reflexión:
“He aquí nuestro Dios a quien servimos pude
librarnos del horno de fuego”
Daniel 3:17
Tema: GRÁFICOS ESTADÍSTICOS: Gráfico de Barras
Objetivo:
 Reconocer el gráfico de barras
 Realizar gráficos de barras
Conocimientos previos: Tabla de frecuencias
Materiales: Escuadras, lápiz
Conceptos:
GRÁFICO DE BARRAS: Se preguntó a 45 personas sobre el equipo favorito de fútbol de
Antioquia. Se obtuvo la siguiente tabla:
Nacional
Envigado
Medellín
Total
20
10
15
45
En este gráfico se ubican en el eje horizontal la variable estudiada (Equipos favoritos de
Antioquia) y por medio de barras verticales se representa la frecuencia absoluta, dependiendo de
la frecuencia es la altura de la barra, todas las bases de las barras son del mismo tamaño y lo que
varía es la altura.
EQUIPO DE FÚTBOL FAVORITOS DE
ANTIOQUIA
25
20
15
No de personas
10
5
0
Nacional
Envigado
Medellín
En el gráfico se observa que el equipo favorito es El Nacional
Actividad:
1. Realizar una pregunta de investigación, construir la tabla de frecuencias y el
gráfico de barras
Gep/15
4
Institución Educativa María Montessori Docente: Gloria Pacheco
Unidad de aprendizaje “Estadística”
Grado6º _____________________
Fecha___________________
Nombre y apellido del estudiante__________________________________________________
Reflexión:
“Todas las obras de Dios son verdaderas y sus caminos
justos y Él puede humillar a los que andan con soberbia”
Daniel 4:37
Tema: GRÁFICOS ESTADÍSTICOS: Gráfico Circular
Objetivo:
 Reconocer el gráfico circular
 Realizar gráficos circulares
Conocimientos previos: Tabla de frecuencias
Materiales: Compás, escuadra, transportador, lápiz
Conceptos:
GRÁFICO CIRCULAR:
Deportes preferidos de 50 estudiantes.
Deporte
Nº de
estudiantes
Fútbol
Basquet
Bolybol
Otros
Total
20
15
10
5
50
Para representar el gráfico circular se debe calcular que área del círculo en grados corresponde a la frecuencia
absoluta de la variable estudiada. Así para saber qué área corresponde al fútbol que fue escogido como el deporte
preferido por 20 estudiantes de un total de 50. Se realiza el siguiente procedimiento.
Nº de estudiantes
50

20

Grados
360º
X
(20).(360º)
 144º
50
Luego el área que corresponde al fútbol es 144º
Asimismo se calcula el área para cada uno de los otros deportes.
Básquet
Nº de estudiantes
Grados
50

360º
15

X
X 
(15).(360º)
 108º
50
El área que corresponde a básquet es de 108º
X 
5
Institución Educativa María Montessori Docente: Gloria Pacheco
Unidad de aprendizaje “Estadística”
Grado6º _____________________
Fecha___________________
Nombre y apellido del estudiante__________________________________________________
Voleibol
Nº de estudiantes
50

10

Grados
360º
X
(10).(360º)
 72º
50
El área que corresponde a voleibol es de 72º
X 
Otros
Nº de estudiantes
50

5

Grados
360º
X
(5).(360º)
 36º
50
El área que corresponde a otros es de 36º
X 
Nota: La suma de los grados de todos los deportes escogidos debe dar 360º que es el
área total del círculo.
Veamos:
Fútbol
Básquet
Voleibol
Otros
Total
144º
108º
72º
36º
3 60º
Deporte preferido
Otros; 5
Bolybol; 10
Fútbol; 20
Basquet; 15
Para representar el gráfico circular se hace necesario utilizar el transportador.
Actividad: Realizar una pregunta de investigación, construir la tabla de frecuencias y el
gráfico circular
Gep/15
6
Institución Educativa María Montessori Docente: Gloria Pacheco
Unidad de aprendizaje “Estadística”
Grado6º _____________________
Fecha___________________
Nombre y apellido del estudiante__________________________________________________
Reflexión: Riquezas, honra y vida son la remuneración de la humildad
y del temor de Jehová
Proverbios 22:4
Tema: PROBABILIDAD
Objetivo: Comprender el concepto de probabilidad a través de
la resolución de problemas
Conocimientos previos: División de números naturales
CONCEPTO: Las probabilidades constituyen una rama de las matemáticas que se ocupa de medir o
determinar cuantitativamente la posibilidad de que un suceso o experimento produzca un determinado
resultado. La probabilidad está basada en el estudio de la combinatoria y es fundamento necesario de la
estadística.
ORIGEN: La creación de la probabilidad se atribuye a los matemáticos franceses del siglo XVII Blaise
Pascal y Pierre de Fermat, aunque algunos matemáticos anteriores, como Gerolamo Cardano en el siglo
XVI, habían aportado importantes contribuciones a su desarrollo.
La probabilidad matemática comenzó como un intento de responder a varias preguntas que surgían en
los juegos de azar, por ejemplo saber cuántas veces se han de lanzar un par de dados para que la
probabilidad de que salga seis sea el 50 por ciento.
La probabilidad de un resultado se representa con un número entre 0 y 1, ambos inclusive. La
probabilidad 0 indica que el resultado no ocurrirá nunca, y la probabilidad 1 que el resultado ocurrirá
siempre. Los problemas más sencillos estudian la probabilidad de un suceso favorable en un experimento
o acontecimiento con un número finito de resultados, todos ellos con igual probabilidad de ocurrir.
Si un experimento tiene n posibles resultados, y f de ellos se consideran favorables, la probabilidad de un
suceso favorable es f/n. Por ejemplo, un dado no trucado se puede lanzar de seis formas posibles, por
tanto, la probabilidad de que salga un 5 ó un 6 es 2/6.
Métodos de medición de Probabilidad
Uno de los métodos más utilizados es aplicando la Regla de Laplace: define la probabilidad de un suceso
como el cociente entre casos favorables y casos posibles.
Ejemplos:
a) Probabilidad de que al lanzar un dado salga el número 2: el caso favorable (f) es tan
sólo uno (que salga el dos), mientras que los casos posibles (n) son seis (puede salir
cualquier número del uno al seis).
Por lo tanto:
(o lo que es lo mismo, 16,6%)
b) Probabilidad de que al lanzar un dado salga un número par: en este caso los
casos favorables (f) son tres (que salga el dos, el cuatro o el seis), mientras que
los casos posibles (n) siguen siendo seis.
Por lo tanto:
(o lo que es lo mismo, 50%)
c) Probabilidad de que al lanzar un dado salga un número menor que 5: en este caso tenemos cuatro
casos favorables (f) (que salga el uno, el dos, el tres o el cuatro), frente a los seis casos posibles.
Por
lo
tanto:
(o lo que es lo mismo, 66,6%)
d) Probabilidad de ganarse el premio mayor de una lotería en la que juegan 100.000 números nos: tan
sólo un caso favorable (f), el número que jugamos, frente a los 100.000 casos posibles (n).
Por lo tanto:
(o lo que es lo mismo, 0,001%)
7
Institución Educativa María Montessori Docente: Gloria Pacheco
Unidad de aprendizaje “Estadística”
Grado6º _____________________
Fecha___________________
Nombre y apellido del estudiante__________________________________________________
d) Probabilidad al lanzar una moneda, con un águila en una cara y un sol en la
otra. Hay dos casos posibles (n) de ocurrencia (o cae águila o cae sol) y sólo un
caso favorable (f) de que pueda caer águila (pues sólo hay un águila en la
moneda).
Por lo tanto:
(o,
Existe
una
probabilidad
lo
del
que
50%
de
es
obtener
un
lo
mismo,
águila
al
tirar
50
una
%)
moneda.
e) Probabilidad de elegir tal o cual fruta. Si en una canasta hay 20 peras y 10 manzanas. ¿Qué fruta es
más
probable
que
saque
al
azar
de
la
canasta?
Para este ejemplo tenemos que 30 es el total de frutas en la canasta; es decir los casos posibles (n).
Para calcular la probabilidad de sacar una manzana los casos favorables (f) son 10 puesto que existen
sólo 10 manzanas.
Por lo tanto:
(o, lo que es lo mismo, 33,3 %)
(o, lo que es lo mismo, 66,7 %)
Fíjate bien que 33,3% + 66,7% es igual al 100% porque siempre que saquemos algo de
la canasta es seguro que será una fruta.
Condiciones importantes
Para poder aplicar la Regla de Laplace el experimento aleatorio tiene que
cumplir dos requisitos:
a) El número de resultados posibles (sucesos o eventos) tiene que ser finito. Si
hubiera infinitos resultados, al aplicar la regla "casos favorables dividido por
casos posibles" el cociente siempre sería cero.
b) Todos los sucesos o eventos tienen que tener la misma probabilidad. Si al lanzar un dado, algunas
caras tuvieran mayor probabilidad de salir que otras, no podríamos aplicar esta regla.
A la regla de Laplace también se le denomina "probabilidad a priori", ya que para aplicarla hay que
conocer antes de realizar el experimento cuales son los posibles resultados y saber que todos tienen las
mismas probabilidades.
P r o b l e ma s d e p r o b a b i l id a d
1. Busca la probabilidad de que al echar un dado al aire, salga:
a.
b.
c.
2.
Un número par.
Un múltiplo de tres.
Un número Mayor que cuatro.
Se lanzan dos dados al aire y se anota la suma de los puntos obtenidos. Se pide:
a.
b.
c.
d.
Escribir el espacio
La probabilidad de
La probabilidad de
La probabilidad de
muestral
que salga el 7.
que el número obtenido sea par.
que el número obtenido sea múltiplo de tres.
3.
Una urna tiene ocho bolas rojas, 5 amarilla y siete verdes. Se extrae una al azar
de que:
a. Sea roja.
b. Sea verde.
c. Sea amarilla.
d.
No sea roja.
e. No sea amarilla.
Respuestas: http://www.vitutor.com/pro/2/a_g.html Gep/15
8