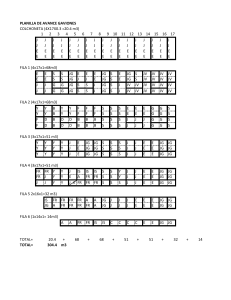
GRUPO 1 INTEGRANTES: - Espinoza Yupanqui Piero Alessandro - Rivas Chamorro Alexis Eduardo - Romaní Rodríguez Nadia Patricia Problema 1 Maximizar Z = 2X1 + 5X2 + 8X3 s.a. 6*X1 + 8*X2 + 4*X3 ≤ 96 2*X1 + X2 + 2*X3 ≤ 40 5*X1 + 3*X2 + 2*X3 ≤ 60 X1, X2, X3 ≥ 0 PASO 1: Igualar la función objetivo a cero junto con las restricciones: 1*Z – 2*X1 – 5*X2 – 8*X3 + 0*S1 + 0*S2 + 0*S3 = 0 0*Z+ 6*X1 + 8*X2 + 4*X3 + 1*S1 + 0*S2 + 0*S3 = 96 0*Z + 2*X1 + 1*X2 + 2*X3 + 0*S1 + 1*S2 + 0*S3 = 40 0*Z+ 5*X1 + 3*X2 + 2*X3 + 0*S1 + 0*S2 + 1*S3 = 60 PASO 2: Colocar los datos en la tabla simplex: 96/4 = 24 40/2 = 20 60/2 = 30 PASO 3: Identificar la columna pivote Donde entrara una variable Maximización: La variable más negativa PASO 4: Identificar la fila pivote Donde saldra una variable Es el menor valor de la división entre la columna solución y la columna pivote sin considerar la fila de función objetivo PASO 5: Intersectar y obtener el elemento pivote Identificado el elemento pivote, lo convertimos en 1 y en ceros los numeros por encima y por debajo de este elemento Fila 3 se multiplica por 1/2 Fila 1 se suma con 8 veces la fila 3, fila 2 se resta con 4 veces la fila 3 y fila 4 se resta con 2 veces la fila 3 PASO 6: Repetir los procedimientos anteriores. 16/6 = 8/3 20/0.5 = 40 20/2 = 10 Fila 2 se multiplica por 1/6 Fila 1 se suma con la fila 2, fila 3 se resta con la mitad de la fila 2 y fila 4 se resta con 2 veces la fila 2 De la tabla: X1 = 0, X2 = 8/3, X3 = 56/3, S3 = 44/3 y Z = 488/3 Comprobando los valores usando el POM Problema 2 Minimizar Z = 3X1 + 2X2 s.a. 2X1 + X2 ≤ 2 3X1 + 4X2 ≥ 12 X1, X2 ≥ 0 PASO 1: Igualar la función objetivo a cero junto con las restricciones y a las desigualdades mayores o iguales a un valor agregarle una variable artificial. 1*Z – 3*X1 – 2*X2 + 0*S1 + 0*S2 - M*A2 = 0 0*Z+ 2*X1 + 1*X2 + 1*S1 + 0*S2 + 0*A2 = 2 0*Z + 3*X1 + 4*X2 + 0*S1 - 1*S2 + 1*A2 = 12 PASO 2: Colocar los datos en la tabla simplex: Entran en la tabla de las filas las variables a la derecha de X1 y X2 positivas Fila 1 se multiplica por m veces la fila 3 PASO 3: Identificar la columna pivote Donde entrara una variable Minimización: La variable más positiva PASO 4: Identificar la fila pivote Donde saldra una variable Es el menor valor de la división entre la columna solución y la columna pivote sin considerar la fila de función objetivo PASO 5: Intersectar y obtener el elemento pivote Identificado el elemento pivote, lo convertimos en 1 y en ceros los numeros por encima y por debajo de este elemento 2/1 = 2 12/4 = 3 Fila 1 se suma con (2-4M) veces la fila 2 y fila 3 se resta con 4 veces la fila 2 Como se observa una variable artificial, deducimos que no existe solución En especifico es una solución no factible Metodo Grafico Se confirma que no existe solución Problema 3 La empresa Whitt Windows tiene solo tres empleados que hacen dos tipos de ventanas: con marco de madera y con marco de aluminio, la ganancia es de $60 por cada ventana con marco de madera y de $30 por cada una con marco de aluminio. Doug hace marcos de madera, y puede terminar 6 al día, Linda hace 4 marcos de aluminio al día, Bob forma y corta el vidrio y puede hacer 48 pies cuadrados de vidrio por día, cada ventana con marco de madera usa 6 pies cuadrados de vidrio y cada de aluminio usa 8 pies cuadrados de vidrio. La compañía desea determinar cuántas ventanas de cada tipo producir al día para maximizar la ganancia total. a) Formule el modelo de programación lineal. b) Use el método grafico para resolver el modelo. c) Un nuevo competidor en la ciudad también produce ventanas de madera, esto puede forzar a la compañía a bajar sus precios y por ende la ganancia debida a este tipo de ventanas. ¿Cómo cambiara la solución óptima (si cambia) si la ganancia por ventana de madera disminuye de $ 60 a $ 40 y de $ 60 a $ 20?. d) Doug piensa reducir sus horas de trabajo, lo cual reducirá el número de ventanas de madera por día. ¿Cómo cambiara la solución óptima si hace solo 5 marcos diarios? PASO 1: DEFINIR VARIABLES DE DECISIÓN A: # ventanas con marco de aluminio M: # ventanas con marco de madera PASO 2: DEFINIR FUNCIÓN OBJETIVO Maximizar la ganancia total. $ 30*A + 60* M PASO 3: RESTRICCIONES Restricción 1: Límite de capacidad de producción de marcos de madera Restricción 2:Límite de capacidad de producción de marcos de aluminio M≤6 A≤4 Restricción 3: Límite de capacidad de producción de 8A + 6M ≤ 48 vidrio para cualquier ventana (1 , 6) (1.5 , 6) Debido a que las variables de decisión deben ser enteras (# de ventanas) ZONA FACTIBLE $ 30*(1) + 60* (6) --> $390 c) Se disminuye el precio de ventanas de madera $ 30*A + ↓60* M --> $390↓ $ 30*A + 59* M --> $384 $ 30*A + 58* M --> $378 -$6 …. $ 30*A + 41* M --> $276 $ 30*A + 40* M --> $270 La solución óptima sigue siendo (1,6) cuando la ventana de madera se vende en $40. -$6 8*A + 6* M 30A+ k*M 8/30=6/k --> k= 22,5 Este valor es la mínimo de k. Nos indica el límite de rango de optimalidad: k ≥ 22,5 Es de decir que si k= 20 < 22,5 ; la solución óptima ya no será (1,6) $ 30*A + 24* M --> $174 $ 30*A + 23* M --> $168 $ 30*A + 22.5* M --> $165 $ 30*A + 22* M --> $162 $ 30*A + 21* M --> $156 $ 30*A + 20* M --> $150 (4 ,2.667)La solución óptima sigue siendo (1,6). (4 ,2) ≥ ≥ = ≤ ≤ ≤ $ 30*A + 24* M --> $168 $ 30*A + 23* M --> $166 $ 30*A + 22.5* M --> $165 $ 30*A + 22* M --> $164 $ 30*A + 21* M --> $162 $ 30*A + 20* M --> $160 La solución óptima cuando la ventana de madera se vende a 20$ es (4,2) $ 30*A + 60* M d) Menos producción de marcos de madera M≤6 ↓ A≤4 8A + 6M ≤ 48 (1.5 ,6) (2.25 ,5) (3 ,4) (4 ,2,667) $ 30*A + 60* M --> $405 $ 30*A + 60* M --> $367.5 $ 30*A + 60* M --> $330 $ 30*A + 60* M --> $280 Precio sombra: - $37,5 / hora -$37.5 Problema 4 Carne con papas es el plato favorito de Ralph Edmund. Por eso decidió hacer una dieta continua de solo estos dos alimentos (más algunos líquidos y suplementos de vitaminas) en todas sus comidas. Ralph sabe que no es la dieta más sana y quiere asegurarse de que toma las cantidades adecuadas de los dos alimentos para satisfacer los requerimientos nutricionales. Cuenta con la siguiente información nutricional y de costo: Problema 4 PASO 1: DEFINIR VARIABLES DE DECISIÓN R: # Porcines de carne en la dieta diaria P: # Porcines de papa en la dieta diaria PASO 2: DEFINIR FUNCIÓN OBJETIVO Minimizar el costo total. $ 4*R + 2*P A) Formular el Modelo de PPL Zmax= $4*R + $2*P PASO 3: RESTRICCIONES Restricción 1: Gramos de Carbohidratos que requiere diariamente $5*R +$1 5*P ≥ $50 Restricción 2: $20*R +$5*P≥ $40 Gramos de Proteinas que requiere diariamente $15*R + $2*P≥ $60 Restricción 3: Gramos de Grasas que requiere diariamente B) Resolver el modelo por método gráfico Zona Factible Solucion Optima La solucion optima es el vertice mas cercano a la funcion objetivo por ser un problema de minimizacion La solucion optima esta en la interseccion entre las restricciones 1 y 3 5*R +1 5*P = 50 15*R +2*P = 60 P= 90/43 2.093 raciones R= 160/43 =3.721 raciones Z min = 2* 2.093+4*3.721 Z min = 19.07$ C) Analisis de sensibilidad para costos marginales de cada tipo de porcion El costo de cada porcion(dejando el otro costo constante) puede variar en un rango tal que la solucion optima sea la misma. Para el precio de papas (-2/15 ≥ -c1/4 ≥ -3) *-1 (3 ≥ c1/4 ≥ 2/15)*4 (12 ≥ c1 ≥ 8/15) Rango marginal para el precio de porcion de papa Para el precio de Res (-2/15≥ -2/c2 ≥ -3)*-1 (3 ≥ 2/c2 ≥ 2/15)^-1 (15/2 ≥ c2/2 ≥ 1/3)*2 Rango marginal para el precio de porcion de Res (15 ≥ c2 ≥ 2/3) Para el precio dual de proteina L1' ^ L3 (5*R+15*P=49) PD=Z-Z'=19.07-18.926 (15*R+2*P=60) R= 3.72 P=2.023 Z'=18.926 PD = 0.144$ Para el precio Limite de proteina L3 ^Y P=0 15*R+2*P=60 R=4 P=0 Z'=16 El Limite para L1 es: 5*R+15*P ≥ 20 D)Hallar precio dual y limite de carbohidratos, proteinas y grasas Para el precio dual de grasas L3'^L2 5*R+15*P=50 ) PD=Z-Z'=19.07-18.836 (15*R+2*P=59) R= 3.651 P=2.116 Z'=18.836 PD= $ 0.234 Para el precio Limite de grasas L1^L2 5*R+15*P=50 20*R+5*P=40 R=1.273 P=2.909 El limite de L3 es: 15*R+2*P ≥ 24.913 D)Hallar precio dual y limite de carbohidratos, proteinas y grasas Para el precio dual de carbohidratos L2'^L1 20*R+5*P=41 ) (5*R+15*P=50) PD= Z-Z'=0 R= 1.327 P=2.89 Z'=19.07 Para el precio Limite de carbohidratos L1^L3 (5*R+15*P=49 ) (15*R+2*P=60) R= 3.72 P=2.023 El limite de L2 es: 20*R+5*P ≥ 84.515