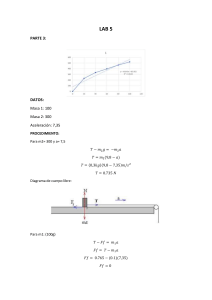
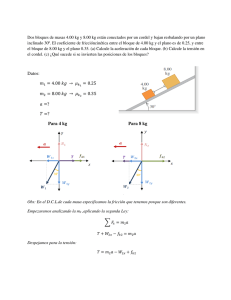
Problemario de Leyes de Newton 1) Un patinador de 75.5 kg, que se desliza inicialmente a 3.50 m/s sobre hielo áspero horizontal, llega al reposo de manera uniforme en 1.5 s debido a la fricción del hielo. a) ¿Qué fuerza ejerce la fricción sobre el patinador? b) ¿Cuál es el coeficiente de fricción? c) ¿Cuál es la aceleración? 2) Si el coeficiente de fricción cinética entre neumáticos y pavimento seco es de 0.95 a) ¿cuál es la distancia mínima para que se detenga un automóvil que viaja a 80 km/h bloqueando los frenos? 3) Considere el sistema de la figura. El bloque A pesa 55.0 N y el bloque B pesa 35.0 N. Una vez que el bloque B se pone en movimiento hacia abajo, desciende con rapidez constante. a) Calcule el coeficiente de fricción cinética entre el bloque A y la superficie de la mesa. 4) Un objeto de 13.00 kg está sujeto a cuatro fuerzas que dan una aceleración 𝑎⃗ = −(13.75 𝑚/𝑠 2 )𝑖 + (6.50 𝑚/𝑠 2 )𝑗. Si tres de las cuatro fuerzas son ⃗⃗⃗⃗ ⃗⃗⃗⃗2 𝐹1 = (38.0𝑁)𝑖̂ − (6𝑁)𝑗̂ , ⃗⃗⃗⃗ 𝐹2 = −(12𝑁)𝑖 + (8𝑁)𝑗 y ⃗⃗⃗⃗ 𝐹3 = 2𝐹 a) ¿Cuánto vale la cuarta fuerza? 5) Se aplica una Fuerza horizontal de 355 N a una caja en reposo, que se encuentra sobre un plano horizontal con coeficiente de fricción cinético de 0.19. Si la masa de la caja es de 96 kg, a) calcule la velocidad de la caja a los 15.0 s. 6) En un plano inclinado 35° por encima de la horizontal, se encuentra una caja de 65 kg inicialmente en reposo. El coeficiente de fricción cinemático y estático, entre la caja y el plano inclinado tienen un valor de 0.77. Si luego se aplica a la caja una fuerza paralela al plano con valor de 680 N, para subir la caja tangencialmente al plano inclinado, a) calcule la aceleración de la caja. 7) Una bola de bolos pesa 71.2 N. El jugador aplica una fuerza horizontal de 160 N a la bola. a) ¿Qué magnitud tiene la aceleración horizontal de la bola? 8) Un hombre arrastra hacia arriba un baúl por la rampa de un camión de mudanzas. La rampa está inclinada 20º y el hombre tira con una fuerza 𝐹⃗ cuya dirección forma un ángulo de 30° con la rampa (figura). a) ¿Qué 𝐹⃗ se necesita para que la componente 𝐹⃗𝑥 paralela a la rampa sea de 60N? b) ¿Qué magnitud tendrá entonces la componente 𝐹⃗𝑦 perpendicular a la rampa? 9) El “columpio gigante” de una feria local consiste en un eje vertical central con varios brazos horizontales unidos a su extremo superior (figura). Cada brazo sostiene un asiento suspendido de un cable de 5.00 m, sujeto al brazo en un punto a 3 m del eje central a) Calcule el tiempo de una revolución del columpio, si el cable forma un ángulo de 30° con la vertical. b) ¿El ángulo depende del peso del pasajero para una rapidez de giro dada? 10) Un bloque de 106𝑁 cuelga de tres cuerdas, como se muestra en la figura, determine los valores de las tensiones 𝑻𝟏 𝒚 𝑻𝟐 11) Una caja con una masa de 50Kg es arrastrada a través del piso con una cuerda que forma un ángulo de 30° con la horizontal. a) ¿Cuál es el valor aproximado del coeficiente de rozamiento cinético entre la caja y el piso si una fuerza de 250 N sobre la cuerda es requerida para mover la caja con rapidez constante de 20 m/s como se muestra en el diagrama? b) ¿Cuál es el coeficiente de fricción estático? 12) Una fuerza F es usada para sostener un bloque de masa 𝑚 = 50 𝑘𝑔 sobre un plano inclinado como se muestra en la figura. El plano forma un ángulo con la horizontal de 20° y 𝐹⃗ es perpendicular al plano. El coeficiente de fricción entre el plano y el bloque es de 𝜇 = 0.29. a) ¿Cuál es la mínima fuerza ⃗𝑭⃗, necesaria para mantener el bloque en reposo?