3.1 Guía de estudio Ingenierias

Guía para examen de nuevo ingreso
Área de
Ingenierías
Todas excepto, Bioquímica
Tecnológico Nacional de México
Instituto Tecnológico de Morelia. Departamento de Desarrollo Académico.
Í NDICE GENERAL
1
I Examen de Admisión
2
P ENSAMIENTO M ATEMÁTICO
3
1.1
3
3
Razonamiento Aritmético
Jerarquía de operaciones básicas.
1.2
Razonamiento geométrico.
Puntos, segmentos y plano cartesiano.
1.3
Razonamiento trigonométrico.
Funciones trigonométricas.
3
4
11
11
1.4
Razonamiento Algebraico
16
1.5
Razonamiento Estadístico y probabilístico
33
33
37
39
40
42
Frecuencias e información gráfica
Medidas descriptivas
Medidas de dispersión
Medidas de posición
Nociones de probabilidad
2
5
5
P ENSAMIENTO A NALÍTICO
45
2.1
Integración de la información
45
2.2
Interpretación de relaciones lógicas
50
2.3
Estructura de la lengua
55
I NGLÉS COMO LENGUA EXTRANJERA
64
3.1
Comprensión lectora
64
3.2
Uso de la grámatica
64
II Examen Diagnóstico
65
M ATEMÁTICAS
66
4.1
Aritmética
Línea recta.
4.2
Geometría
66
73
86
II
5
4.3
Cálculo de perímetros y áreas de figuras planas
91
4.4
Figuras geométricas: perímetro, área y volumen
93
4.5
Pendiente de la recta y ángulo entre rectas
94
4.6
Ecuaciones y gráficas de la circunferencia, la parábola, la elipse y la hipérbola
95
4.7
Cálculo diferencial
99
4.8
Operaciones con funciones
103
4.9
Límite de una función
105
4.10
Derivada de una función
106
4.11
Integral definida
107
F ÍSICA
110
5.1
Fundamentos teórico-prácticos
110
5.2
Mecánica
115
5.3
Termometría
138
138
Ejemplos
5.4
Calor
139
5.5
Transferencia de calor
140
5.6
Termodinámica
140
141
Ejercicios:
5.7
Electricidad
5.8
Circuitos eléctricos
Ejercicios:
Circuitos en serie.
Circuitos de resistencias en paralelo
5.9
6
Óptica y acústica
P ROBABILIDAD Y E STADÍSTICA
142
142
144
144
145
146
154
6.1
Estadística descriptiva
154
6.2
Probabilidad
158
6.3
Variables Aleatorias
167
6.4
DISTRIBUCIONES DE PROBABILIDAD-Discretas
168
6.5
DISTRIBUCIONES DE PROBABILIDAD-Continuas
175
D OCENTES PARTICIPANTES
180
2
Parte I
Examen de Admisión
1
1.1
1.1.1
3
Pensamiento Matemático
Razonamiento Aritmético
Jerarquía de operaciones básicas.
Signos de agrupación
En palabras sencillas, son los signos que agrupan o delimitan operaciones entre números y se
representan con los siguientes símbolos:
Llave: {}, Corchete: [] y Paréntesis: ()
Operaciones con signo de agrupación.
Son operaciones que involucran signos de agrupación, los que se suprimen al multiplicar por
el número o signo que le antecede, en caso de existir varios signos de agrupación se procede
de dentro hacia fuera.
Si en una expresión algebraica encontramos más de un tipo de operación siempre se comienza
desde el interior hasta el exterior, con el siguiente orden:
p
1. Resolver Potencias o raíces: n x ó x n
2. Multiplicación ó división: × ó ÷
3. Sumas y restas +, −
1.1
Signos de agrupación
a) −(8 − 15) = −8 + 15 = 7
a)27
b)7
c)42
d )41
e)19
b) 7 + 3(7 − 2) − (4 − 9) = 7 + 21 − 6 − 4 + 9 = 37 − 10 = 27
a)8
b)27
c)42
d )41
e)19
c) −5 + 43 − (2 − 5) = −5 + 43 − 2 + 5 = −5 + 12 − 8 + 20 = 32 − 13 = 19
a)9
b)7
c)42
d )41
e)19
d ) 3 − −3[4 + 5 − (−5 + 8) + 6] − 2 = 3 − −3[15 − (3)] − 2 = 3 − −3[15 − 3] + −2 = 3 −
−3[12] + −2 = 3 − −36 − 2 = 3 − −38 = 3 − 38 = 41
a)27
b)43
c)42
d )41
e)19
e) 3 × 5 − 2(8 − 5)2 = 3 × 5 − 2(3)2 = 3 × 5 + 2(9) = 15 − 18 = −3
a)5
f)
b) − 2
c) − 4
d) − 3
4 × 2(3 + 6) 4 × 2(9) 4 × 18 72
=
=
= =24
3
3
3
3
a)3
b)7
c)24
d )41
e)19
e)19
Solución .
1.1.2 Relaciones de proporcionalidad.
Razón.
Se refiere a el cociente de entre dos cantidades
1.2
Signos de agrupación
1) Un automóvil viaja a 120 km por hora y un avión comercial viaja a 1,000 km por hora.
Si ambos tienen rapidez constante, ¿cuántas veces es más rápido el avión que el
automóvil?
1, 000km/h
= 8.3
120km/h
a)7.3
b)8.2
c)8.3
d )8.5
e)9.4
2) En horas normales, el Metro de la Ciudad de México viaja a 75 km
h y un automóvil
recorre 90 metros en 6 segundos. Si ambos tienen rapidez constante, ¿cuántas
veces es más rápido el automóvil que el Metro?
75km 75km
1h
1, 000km
=
·
·
= f r ac(75)(1, 000)3, 600 = 20.83
1h
1h
3, 600s
1km
a)21.83
b)20.83
c)20.83
d )20.85
e)21.84
Solución .
Proporción.
Es la igualdad de 2 razones.
m p
=
n
q
Se lee:
m es a n como p es a q.
Donde:
m y q se llaman extremos, n y q medios.
o’
m : n :: p : q
Proporción directa. Una proporción es directa si al aumentar o disminuir una de las cantidades,
la otra también aumenta o disminuye en la misma proporción.
Definición:
p
Si m es a n como p es a q, entonces m
n = q
1.3
Proporciones directas
Una docena de computadoras se venden en $75, 000. ¿Cuál es el valor de 7 computadoras?
a)43, 850
b)42, 750
c)42, 850
d )43, 700
e)43, 750
Solución .
75, 000 x
=
12
7
1.4
x=
−→
(7)(75, 000) 525, 000
=
= 43, 750
12
12
Proporciones directas
El valor de A varía en proporción directa con B , cuando A = 12, B = 36. ¿Cuál será el valor
de A si B = 21?
a)3
b)7
c)24
d )21
e)19
Solución .
12
A
=
36 21
1.2
1.2.1
−→
A=
(12)(21) 252
=
=7
36
36
Razonamiento geométrico.
Puntos, segmentos y plano cartesiano.
El plano cartesiano es un sistema para representar puntos, rectas, planos por medio de referencias o coordenadas.
Para localizar un punto P en el plano cartesiano se puede tomar como referencia , el origen
en el cruce de los ejes a partir de el. De esta manera se avanza tanto como lo indica el primer
número hacia la derecha o la izquierda y con la nueva posición se mueve hacia arriba o abajo
según lo indique el segundo número.
Puntos y coordenadas: ubicación en el plano cartesiano.
Es un elemento geométrico sin dimensiones cuya posición en el espacio cartesiano de dos dimensiones se identifica mediante un par de números reales x, y.
Para localizar un punto P en el Plano cartesiano se toma como referencia el origen a partir de
él, se avanza tanto como lo indique el primer número (abscisa) hacia la derecha o izquierda,
según sea su signo, y a partir de la nueva posición se avanza hacia arriba o abajo, según lo indique el signo del segundo número (ordenada).
1.5
Puntos en el plano
Ubicar los puntos A(5, 3), B (−1, 7),C (−4, −2) en el plano cartesiano
Solución . 1) El punto A(5, 3)
En el plano cartesiano, en primer lugar se localiza la abscisa x, posteriormente la
ordenada y.
2) El punto B (−1, 7)
3) El punto C (−4, −2)
Puntos que dividen segmentos.
El segmento de una recta se define como la porción de recta limitada por dos puntos no coincidentes.
Es el punto P (x, y) que divide al segmento formado por los puntos P 1 (x 1 , y 1 ) y P 2 (x 2 , y 2 ) en 2
segmentos iguales. Sus coordenadas están dadas por las fórmulas:
x=
1.6
x1 + x2
2
y=
y1 + y2
2
Punto medio
¿Cuáles son las coordenadas del punto medio del segmento que une los puntos P 1 (1, −2)
y P 2 (−3, −3)? a)(2, 7.5)
b)(−3, 7.5)
c)(−2, −7.5)
d )(−2, 7.5)
e)(−2, 7.3)
Solución .
x=
x 1 + x 2 −5 + 1 −4
=
=
= −2
2
2
2
y 1 + y 2 3 + 12 15
=
=
= 7.5
2
2
2
Las coordenadas del punto medio son: (−2, 7.5).
y=
1.7
Punto medio
¿Cuáles son las coordenadas del punto medio del segmento que une los puntos P 1 (−5, 3)
y P 2 (1, 12)? a)(1, −2.5)
b)(−1, −2.5)
c)(−1, 2.5)
d )(−2, −2.5)
e)(−1, −1.5)
Solución .
x=
x 1 + x 2 1 − 3 −2
=
=
= −1
2
2
2
y 1 + y 2 −2 − 3 −5
=
=
= −2.5
2
2
2
Las coordenadas del punto medio son: (−1, −2.5).
y=
Línea recta.
Definición 1.1
Línea recta
La línea recta es el lugar geométrico de todos los puntos tales que si se toman 2 cualesquiera, el valor de la pendiente es constante.
Existen dos formulas para obtener la ecuación de una línea recta.
1. Punto-pendiente. Para hallar la ecuación de la recta que pasa por el punto P 1 (x 1 , y 2 ) y
tiene pendiente m, se utiliza la siguiente fórmula:
y − y 1 = m(x − x 1 )
2. Dados dos puntos. Para determinar la ecuación de la recta que pasa por los puntos
P 1 (x 1 , y 1 ) y P 2 (x 2 , y 2 ), se utiliza la siguiente fórmula:
y − y1 =
y2 − y1
(x − x 1 )
x2 − x1
Formas de representar la ecuación de la recta.
General. Es la forma más común de representar la ecuación de una recta y se obtiene al igualar
a cero.
ax + b y + c = 0
Ordinaria. Con esta forma se determina la pendiente de la recta, así como la intersección de la
misma en el eje Y, se obtiene despejando la variable y de la ecuación general.
y = mx + b
1.8
Recta punto-pendiente
La ecuación de la recta en su forma general que pasa por el punto (−2, 5) y tiene pendiente 13 es:
a)x − 3y + 17 = 0
d ) − x − 3y − 17 = 0
b)x + 3y − 17 = 0
e)x + 3y + 17 = 0
c)x − 3y − 17 = 0
Solución .
Al utilizar la fórmula y − y 1 = m(x − x 1 ), se obtiene:
1
y − 5 = (x − (−2))
3
1.9
→
3(y − 5) = 1(x + 2)
→
3y − 15 = x + 2
→
x + 2 − 3y + 15 = 0
→
x − 3y − 17 = 0
Recta que pasa por 2 puntos
¿Cuál es la ecuación de la recta en su forma general, que pasa por los puntos P 1 (2, −5) y
P 2 (−6, 3)?
a)x − y + 3 = 0
b)x + y − 3 = 0
c) − x + y + 3 = 0
d )x + y + 3 = 0
e)x − y − 3 = 0
Solución .
Se aplica la fórmula; y − y 1 =
y − (−5) =
y 2 −y 1
x 2 −x 1 (x − x 1 ).
3 − (−5)
(x − 2)
−6 − 2
→
8
(x − 2)
−8
y + 5 = −1(x − 2)
→
x + y +3 = 0
→
y +5 =
Graficación de rectas.
Existen varios métodos para obtener la gráfica de una recta, para esta guía utilizaremos el método de la forma ordinaria de la recta. En la siguiente imagen se explica brevemente los elementos
que deben tomarse en cuenta para graficar la recta.
Figura 1. Elementos a considerar para graficar una recta.
1) La gráfica de la recta y = 2x − 5, es:
La ecuación y = 2x − 5, tiene la forma ordinaria y = mx + b, entonces m = 2 y b = −5, es
necesario que la pendiente sea una fracción, por tanto la pendiente se puede expresar
como:
m=
3
Movi mi ent over t i c al
=
2 Movi mi ent ohor i zont al
Se ubica la intersección con el eje y, el punto (0, b) = (0, −5)
Se gráfica la pendiente a partir de la intersección realizando un movimiento horizontal y
tres verticales, como lo muestra la figura.
Por último, la gráfica de la recta es aquella que pasa por los puntos indicados.
2) La gráfica de la recta y = − 23 x + 2, es:
De acuerdo con la recta, el punto de intersección con el eje y es (0, 2) y la pendiente
m = −3
2 .
1.3
1.3.1
Razonamiento trigonométrico.
Funciones trigonométricas.
Función seno
Seno de un ángulo. Es la razón entre el cateto opuesto y la hipotenusa.
Coseno de un ángulo. Es la razón entre el cateto adyacente y la hipotenusa.
Tangente de un ángulo. Es la razón entre el cateto opuesto y el cateto adyacente.
1.5.2 Triángulos rectángulos u oblicuángulos.
Razones trigonométricas.
Las relaciones que existen entre los lados de un triángulo rectángulo, se conocen como funciones trigonométricas.
Figura 2. La figura muestra un triángulo rectángulo, donde: Hi es la hipotenusa, C.O. es el
cateto opuesto y C. A. es el cateto adyacente.
Función Trigonométrica
Seno
C oseno
Teng ent e
C ot ang ent e
Sec ant e
C osec ant e
1.10
Razón
.O.
SenΘ = CHi
C .A.
C osΘ = Hi
TanΘ = CC.O.
.A
.A.
C t g Θ = CC .O.
SecΘ = CHi
.A.
C scΘ = CHi
.O.
Triángulo rectángulo
De la siguiente figura obtenga el ángulo α
a)40◦
b)35◦
c)45◦
d )55◦
e)50◦
Solución .
De la razón trigonométrica
de coseno, podemos despejar al ángulo α en este caso, por lo
³ ´
tanto: α = cos −1
p1
2
= 45◦
1.11
Triángulo rectángulo
De acuerdo con el triángulo de la figura, halla el valor del ángulo A, sabiendo que a = 5 y
b = 3. De acuerdo al triángulo rectángulo.
a)59.003◦
b)59.03◦
c)69.03◦
d )49.03◦
e)59.3◦
Solución .
De acuerdo con el ángulo A , a = 5 cateto opuesto y b = 3 cateto adyacente, al sustituir
los valores de a y b en la definición de la función tangente se obtiene:
C .O. 5
=
C .A. 3
µ ¶
5
= 59.03◦
A = Tan −1
3
tan A =
Problemas con ley de senos y cosenos.
Un triángulo es oblicuángulo cuando sus tres ángulos son oblicuos, es decir, no tiene un ángulo
recto. Este tipo de triángulos se resuelven mediante la ley de senos, de cosenos o de tangentes.
Ley de senos.
La razón que existe entre un lado de un triángulo oblicuángulo y el seno del ángulo opuesto a
dicho lado es proporcional a la misma razón entre los lados y ángulos restantes.
Figura 3. La figura muestra los elementos de un triángulo oblicuángulo.
La ley de senos esta regida por la siguiente expresión:
a
b
c
=
=
Sen A SenB SenC
Es posible utilizar la ley de senos solo para dos casos:
a) Cuando se conocen dos lados y el ángulo opuesto a uno de ellos.
b) Se conocen dos ángulos y cualquiera de los lados.
1.12
Ley de senos
En el triángulo ABC , se tienen los siguientes datos: b = 13cm, ∠B = 40◦ y ∠C = 60◦ .
Determina los lados y el ángulo restante.
a)B = 80◦ , c = 17.5148y a = 19.9171
b)A = 80◦ , c = 17.5148y a = 19.9171
c)A = 80◦ , a = 17.5148yc = 19.9171
d )C = 80◦ , c = 17.5148y a = 19.9171
e)C = 80◦ , c = 17.5148y a = 19.9171
Solución .
Para encontrar el ángulo faltante, debemos contemplar que la suma interna de todos los
ángulos es igual a 180◦ , por lo tanto:
A = 180◦ − B −C = 180◦ − 40◦ − 60◦ = 80◦
c
13
=
◦
Sen(60 ) Sen(40◦ )
c=
(13)(Sen(60◦ ))
= 17.5148
Sen(40◦ )
a=
(13)(Sen(80))
= 19.9171
Sen(40)
Ley de cosenos.
El cuadrado de un lado de un triángulo oblicuángulo es igual a la suma de los cuadrados de los
lados restantes, menos el doble producto de dichos lados por el coseno del ángulo opuesto al
lado buscado.
La ley de cosenos esta regida por la siguiente expresión:
a 2 = b 2 + c 2 − 2bcC os A
b 2 = a 2 + c 2 − 2acC osB
c 2 = a 2 + b 2 − 2abC osC
Es posible utilizar la ley de cosenos solo para dos casos:
a) Cuando se conocen dos lados y el ángulo comprendido entre ellos.
b) Cuando se conocen los tres lados.
1.13
Ley de cosenos
En el triángulo ABC , a = 15cm, c = 18cm y ∠C = 70◦ , resolver el triángulo.
a)B = 47.6◦ , A = 62.4y a = 19.09
b)A = 47.6◦ ,C = 62.4y a = 19.09
c)B = 47.6◦ ,C = 62.4yb = 19.09
d )C = 47.6◦ , B = 62.4yb = 19.09
e)C = 47.6◦ , B = 62.4y a = 19.09
Solución .
Para calcular el valor de b, se utiliza la siguiente formula:
b 2 = a 2 + c 2 − 2acC osB
Donde:
b=
p
(152 + (18)2 − 2(15)(18)(C os(70◦ ))
b = 19.09
Una vez conociendo los tres lados del triángulo, es posible determinar los ángulos, por
lo tanto ∠ A.
C os A =
b 2 + c 2 − a 2 (19.09)2 + (18)2 − (152 )
=
= 0.6743
2bc
2(19.09)(18)
A = ar cC os(0.6743) = 47.6◦
Para terminar, se determina el último ángulo C.
∠C = 180◦ − 47.6◦ − 70◦ = 62.4◦
1.4
Razonamiento Algebraico
Un polinomio es el resultado de sumar o restar 2 o más términos algebraicos no semejantes; en
específico, será binomio si son 2 términos algebraicos y trinomio si son 3 términos.
Ejemplos:
Expresión algebraica
Nombre
2x + 3y
Binomio
a 2 + 2ab + 3b 2
Trinomio
Suma de polinomios
Al sumar 2 o más polinomios se simplifican los términos semejantes entre los polinomios.
1.14
Suma de polinomios
El resultado de (4a 2 − 5a + 7) + (−2a 2 + 3a − 4) es:
a) 2a 2 − 2a + 3
b) 2a 2 + 2a + 3
c) 2a 2 − 2a − 3
Solución .
d ) 2a 2 + 2a − 3.
Se acomodan los términos semejantes en forma vertical y se respetan los signos de los
términos algebraicos que forman cada uno de los polinomios. Se procede a la simplificación de los términos algebraicos.
4a 2 − 5a + 7
− 2a 2 + 3a − 4
2a 2 − 2a + 3
Por tanto, la opción correcta es el inciso a.
1.15
Suma de polinomios
La suma de 8x + 7y − 11 con −5y + 12x − 2 + 3z es:
a ) 3x + 19y − 13 + 3z
b ) 20x − 2y + 13 − 3z
c ) 3x + 19y + 13 + 3z
d ) 20x + 2y − 13 + 3z
Solución .
Esta operación se realiza también de manera horizontal, se agrupan los términos semejantes y se simplifica al máximo.
8x + 7y − 11 − 5y + 12x − 2 + 3z = 8x + 12x + 7y − 5y − 11 − 2 + 3z
= 20x + 2y − 13 + 3z
Por tanto, la opción correcta es el inciso d.
1.16
Suma de polinomios
¡
¢ ¡
¢
El resultado de 25 x 2 − x y + 13 y 2 + 2x 2 + 3x y + v 41 y 2 es:
7 2
7 2
2
2
a) 12
b) 12
5 x − 2x y + 12 y
5 x + 2x y − 12 y
7 2
7 2
2
2
d) 12
c) 12
5 x + 2x y + 12 y
5 x − 2x y − 12 y
Solución .
Se agrupan y reducen los términos semejantes
µ
¶
µ
¶
2 2
1 2
1 2
2
1 1 2
2
2
x − x y + y + 2x + 3x y + v y =
+ 2 x + (3 − 1) x y + +
y
5
3
4
5
3 4
7
12 2
x + 2x y + y 2
=
5
12
Por tanto, la opción correcta es el inciso c.
Resta de polinomios
Se identifican el minuendo y el sustraendo para realizar la operación:
Minuendo − Sustraendo
Se cambia el signo a cada uno de los elementos del polinomio al cual le antecede el signo menos.
1.17
Resta de polinomios
El resultado de (4x + 3y − 5) − (2x + y − 3) es:
a) 2x − 2y − 2
b) 2x + 2y − 2 c) 2x + 2y + 2
d) 2x − 2y + 2
Solución .
Se eliminan los paréntesis y se simplifican los términos semejantes.
(4x + 3y − 5) − (2x + y − 3) = 4x + 3y − 5 − 2x − y + 3
= (4 − 2)x + (3 − 1)y + (3 − 5)
= 2x + 2y − 2
Por tanto, la opción correcta es el inciso b.
1.18
Resta de polinomios
2
Si a x 3 + 2x − 5x + 7 se resta 2x 2 − 6x + 1, se obtiene:
a) x 3 + x + 6
b) x 3 + x 2 + x + 6
3
c) x − x + 6
d) x 3 − x 2 + x + 6
Solución .
Se establece la operación:
(x 3 + 2x 2 − 5x + 7) − (2x 2 − 6x + 1) = x 3 + 2x 2 − 5x + 7 − 2x 2 + 6x − 1
= x 3 + (2 − 2)x 2 + (−5 + 6)x + (7 − 1)
= x 3 + 0x 2 + x + 6
= x3 + x + 6
Por tanto, la opción correcta es el inciso a.
1.19
Resta de polinomios
Al restar 2x + 3y − 1 de 5x − 7y + 7, se obtiene:
a) 3x − 10y − 8
b) 3x + 10y − 8
c) 3x + 10y + 8
d) 3x − 10y + 8
Solución .
Se establece la operación:
(5x − 7y + 7) − (2x + 3y − 1) = 5x − 7y + 7 − 2x − 3y + 1
= 3x − 10y + 8
Por tanto, la opción correcta es el inciso d.
Multiplicación de polinomios
Para realizar esta operación se consideran la regla de los signos en multiplicación y la ley de los
exponentes para el producto de bases iguales.
1. Regla de los signos:
(+)(+) = +
(−)(−) = +
(+)(−) = (−)(+) = −
2. Ley de los exponentes:
Cuando se multiplican bases iguales, la base permanece y los exponentes se suman.
x n · x m = x n+m
Monomio por monomio
1.20
Monomio por monomio
El resultado de (x 6 )(x 2 ) es:
a) 2x 8
b) 2x 12
c) x 12
d) x 8
Solución .
Al aplicar la ley de los exponentes para el producto de bases iguales:
(x 6 )(x 2 ) = x 6+2 = x 8
Por tanto, la opción correcta es el inciso d.
1.21
Monomio por monomio
El resultado de (−3x 2 y 3 )(4x y 2 ) es:
a) 12x 3 y 5
b) −12x 3 y 5
c) −12x 2 y 6
d) 12x 2 y 6
Solución .
Se realiza el producto de los signos de los coeficientes, y se suman los exponentes para
cada base que se repita.
(−3x 2 y 3 )(4x y 2 ) = (−3)(4)x 2 + 1y 3 + 2
= −12x 3 y 5
Por tanto, la opción correcta es el inciso b.
1.22
Monomio por monomio
El resultado de (− 12 x 3 )(− 32 x y 2 ) es:
a) 43 x 4 y 2
b) − 34 x 4 y 2
c) 34 x 3 y 2
d) − 34 x 3 y 2
Solución .
µ
¶µ
¶ µ ¶µ ¶
1
3
1
3
− x3 − x y 2 = −
− x 3+1 y 2
2
2
2
2
3 4 2
= x y
4
Por tanto, la opción correcta es el inciso a.
1.23
Monomio por monomio
El resultado de (2x)(−3x 2 )(−4x 3 ) es:
6
a) −24x 6
b) 12x
c) −12x 6
d) 24x 6
Solución .
(2x)(−3x 2 )(−4x 3 ) = (2)(−3)(−4)x 1+2+3
= 24x 6
Por tanto, la opción correcta es el inciso d.
Monomio por polinomio
Se realiza el producto del monomio con cada uno de los términos algebraicos que conforman
el polinomio.
1.24
Monomio por polinomio
El resultado de 2x 2 (x 2 + 3x − 4) es:
a) 2x 4 + 6x 2 − 8
b) 2x 4 − 6x 3 − 8x 2
d) 2x 4 − 6x 2 + 8
c) 2x 4 + 6x 3 − 8x 2
Solución .
2x 2 (x 2 + 3x4) = 2x 2 (x 2 ) + 2x 2 (3x) + 2x 2 (−4)
= 2x 2 + 2 + 6x 2 + 1 − 8x 2
= 2x 4 + 6x 3 − 8x 2
Por tanto, la opción correcta es el inciso c.
1.25
Monomio por polinomio
El resultado de multiplicar −3x y con 2x 3 − 5x y 2 + 6y 4 es:
a) 6x 4 y + 15x 2 y 3 − 18x y 5
b) −6x 4 y + 15x 2 y 3 − 18x y 5
4
2 3
5
c) −6x y + 15x y + 18x y
d) 6x 4 y − 15x 2 y 3 − 18x y 5
Solución .
Se establece la operación:
−3x y(2x 3 − 5x y 2 + 6y 4 ) = −3x y(2x 3 ) − 3x y(−5x y 2 ) − 3x y(6y 4 )
= −6x 4 y + 15x 2 y 3 − 18x y 5
Por tanto, la opción correcta es el inciso b.
Polinomio por polinomio
Cada uno de los elementos del primer polinomio multiplica al segundo, los elementos que
resulten términos semejantes se simplifican.
1.26
Polinomio por polinomio
El resultado de (2x + 5y)(3x − 7y) es: a) 6x 2 + x y − 35y 2
6x 2 + x y + 35y 2
d) ?6x 2 + x y − 35y 2
b) 6x 2 − x y − 35y 2 c)
Solución .
(2x + 5y)(3x − 7y) = 2x(3x − 7y) + 5y(3x − 7y)
= 6x 2 − 14x y + 15x y − 35y 2
= 6x 2 + x y − 35y 2
Por tanto, la opción correcta es el inciso a.
1.27
Polinomio por polinomio
El producto de x 2 + 3x − 2 con x 3 − 5x 2 es:
a) x 5 + 2x 4 − 17x 3 + 10x 2
b) x 5 − 2x 4 ? − 17x 3 + 10x 2
5
4
3
2
c) x − 2x + 17x + 10x
d) x 5 + 2x 4 − 17x 3 − 10x 2
Solución .
Se realiza la operación de la siguiente manera:
(x 2 + 3x − 2)(x 3 − 5x 2 ) = x 2 (x 3 − 5x 2 ) + 3x(x 3 − 5x 2 ) − 2(x 3 − 5x 2 )
= x 5 − 5x 4 + 3x 4 − 15x 3 − 2x 3 + 10x 2
= x 5 − 2x 4 − 17x 3 + 10x 2
Por tanto, la opción correcta es el inciso b.
División de polinomios
Para realizar esta operación se consideran las leyes de los signos para la división y la de los
exponentes para la división de bases iguales.
1. Leyes de los signos:
+
+
−
−
=+
=+
+
−
=−
−
+
=−
2. Ley de los exponentes: Si se dividen bases iguales, la base permanece y al exponente del
numerador se le resta el exponente del denominador.
xn
xm
= x n−m , para todo x ̸= 0
Monomio entre monomio
1.28
Monomio entre monomio
El resultado de
a) −9x 4
Solución .
−108x 6
−12x 2
es :
b) 4x 4
c) 9x 4
d) −4x 4
4
−108x 6 −108 6−2
=
x
= 9x
2
−12x
−12
Por tanto, la opción correcta es el inciso c.
1.29
Monomio entre monomio
12x 3 y 5
El resultado de −4x 2 y 3 es: a) 3x y 2
b) −3x 2 y
c) 3x 2 y
d) −3x y 2
Solución .
12 3−2 5−3
12x 3 y 5
=
x
y
= −3x y 2
2
3
−4x y
−4
Por tanto, la opción correcta es el inciso d.
1.30
Monomio entre monomio
El resultado de
a) 95 abc 2
18a 3 b 5 c 2
es:
10a 2 b 5
b) 95 a 2 c 2
c) 95 ac 2
d) 59 ab
Solución .
La división de coeficientes no es exacta, entonces se simplifica la fracción:
18a 3 b 5 c 2 18 3−2 5−5 2 9 0 2 9 2
=
a b c = ab c = ac
10a 2 b 5
10
5
5
Por tanto, la opción correcta es el inciso c.
Polinomio entre monomio
Se divide cada uno de los elementos del polinomio entre el monomio.
1.31
Polinomio entre monomio
El resultado de
d) x 2 + 2x − 3
4x 3 +8x 2 −12x
4x
es: a) x 2 −2x −3
b) x 2 +2x +3
Solución .
4x 3 + 8x 2 − 12x 4x 3 8x 2 12x 4 3−1 8 2−1 12 1−1
=
+
−
= x
+ x
− x
4x
4x
4x
4x
4
4
4
Pero todo número elevado a la cero potencia es la unidad, entonces
x 2 + 2x − 3(1) = x 2 + 2x − 3
Por tanto, la opción correcta es el inciso d.
c) x 2 −2x +3
1.32
Polinomio entre monomio
−12x 4 y 3 +15x 2 y 6 −20x 5 y
−6x 2 y
5 5
10 3
2 2
a) 2x y − 2 y + 3 x
3
d) 2x 2 y 2 − 52 x y 5 − 10
3 x y
El cociente de
es:
b) 2x 2 y 2 − 25 x y 5 +
10 3
3 x y
c) 2x 2 y 2 − 52 x y 5 −
10 3
3 x y
Solución .
−12x 4 y 3 + 15x 2 y 6 − 20x 5 y −12x 4 y 3 15x 2 y 6 20x 5 y
=
+
−
−6x 2 y
−6x 2 y
−6x 2 y −6x 2 y
12 4−2 3−1 15 2−2 6−1 20 5−2 1−1
=
x
y
− x
y
+ x
y
6
6
6
10
5
= 2x 2 y 2 − x 0 y 5 + x 3 y 0
2
3
5
10
= 2x 2 y 2 − (1)y 5 + x 3 (1)
2
3
5 5 10 3
2 2
= 2x y − y + x
2
3
Por tanto, la opción correcta es el inciso a.
Binomios conjugados
Son de la forma (a + b)(a − b), su característica principal es que tienen los mismos términos,
pero uno de ellos tiene signo contrario y al realizar el producto se obtiene una diferencia de
cuadrados, esto es:
(a + b)(a − b) = a 2 − b 2
1.33
Binomios conjugados
El resultado de (x + 4)(x − 4) es:
a) x 2 + 16
b) x 2 − 16
c) x 2 − 8x + 16
d) x 2 + 8x + 16
Solución .
Al desarrollar se obtiene: (x + 4)(x − 4) = (x)2 − (4)2 = x 2 − 16
Binomio al cuadrado
Es de la forma (a + b)2 y al desarrollarlo se obtiene un trinomio cuadrado perfecto, esto es:
(a + b)2 = a 2 + 2ab + b 2
Su desarrollo es: el cuadrado de un binomio es igual al cuadrado del primer término, más el
doble producto del primero por el segundo, más el segundo término al cuadrado.
1.34
Binomio al cuadrado
El resultado de (2x − 5y)2 es:
a) 4x 2 − 20x y − 25y 2
c) 4x 2 + 20x y + 25y 2
Solución .
Al desarrollar se obtiene:
b) 4x 2 − 20x y + 25y 2
d) 4x 2 + 20x y − 25y 2
(2x − 5y)2 = (2x)2 + 2(2x)(−5y) + (−5y)2 = 4x 2 − 20x y + 25y 2
Por tanto, la opción correcta es el inciso b.
Bionomio al cubo
Son de la forma (a + b)3 y al desarrollarlos se obtiene un polinomio de cuatro términos.
(a + b)3 = a 3 + 3a 2 b + 3ab 2 + b 3
Su desarrollo es: el cubo de un binomio es igual al cubo del primer término, más el triple producto del primer término al cuadrado por el segundo término, más el triple producto del primero por el cuadrado del segundo, más el cubo del segundo término.
1.35
Binomio al cubo
El resultado de (x + 2)3 es:
b) x 3 − 6x 2 + 12x − 8
a) x 3 − 8
c) x 3 + 8 d) x 3 + 6x 2 + 12x + 8
Solución .
Al desarrollar el binomio se obtiene:
(x + 2)3 = (x)3 + 3(x)2 (2) + 3(x)(2)2 + (2)3
= x 3 + 3(x 2 )(2) + 3(x)(4) + (8)
= x 3 + 6x 2 + 12x + 8
Por tanto, la opción correcta es el inciso d.
Ecuaciones de primer grado con una incógnita.
Una ecuación de primer grado con una incógnita es una igualdad entre 2 expresiones, que
involucran constantes y una incógnita cuyo grado es 1; se conforma de 2 miembros.
Primer miembro = segundo miembro
Al resolver una ecuación de primer grado con una incógnita, se obtiene el valor de la incógnita
que satisface la igualdad.
Resolución de una ecuación de primer grado con una incógnita
Para la resolución de este tipo de ecuaciones se aplican los despejes, los cuales permiten obtener el valor de la incógnita mediante las operaciones inversas.
Operación
Operación inversa
Suma
Resta
Resta
Suma
Multiplicación
División
División
Multiplicación
1.36
Ecuaciones de primer grado
El valor de y que cumple con la igualdad −2(5y + 1) = −4(y + 6) − 2 es:
a) −4
b) 4
c) 3
d) −3
Solución .
Se eliminan los paréntesis en la igualdad:
−2(5y + 1) = −4(y + 6) − 2
−10y − 2 = −4y − 24 − 2
Se agrupan en el primer miembro los términos con la incógnita y en el segundo, los términos independientes.
−10y + 4y = −24 − 2 + 2
Se simplifican los términos semejantes:
−6y = −24
Se despeja la variable y
−24
−6
y =4
y=
Por tanto, la opción correcta es el inciso b.
Problemas que se resuelven con ecuaciones de primer grado con una incógnita.
Se establecen los elementos que intervienen en el problema mediante una incógnita y se realiza
el planteamiento que permita resolver el problema mediante una igualdad.
1.37
Problema
La suma de las edades de dos hermanos no gemelos es de 12 años, la diferencia de sus
edades es el doble de la edad de uno de ellos, ¿cuál es la edad de los hermanos?
a) 6 y 6
b) 9 y 3
c) 7 y 5
d ) 10 y 2
Solución .
Si fueran gemelos la diferencia de sus edades sería cero y la condición no tendría razón
de ser, como esto no ocurre, la edad de los hermanos se obtiene de la siguiente manera:
Edad del hermano menor: x
Edad del hermano mayor: 12 − x
Diferencia de sus edades = doble de la edad de uno de ellos
(12 − x) − x = 2(x)
En el segundo término de la igualdad se toma la edad del hermano menor, ya que si se
aplica la edad del hermano mayor al multiplicarlo por dos el resultado será mayor que la
diferencia. Al resolver la ecuación de primer grado se obtiene que x = 3, entonces:
Edad del hermano menor: x = 3 años
Edad del hermano mayor: 12 − x = 12 − 3 = 9 años
Por tanto, la opción correcta es el inciso b.
Ecuación de segundo grado.
Una ecuación de la forma ax 2 + bx + c = 0 , con a, b y c ∈ R y a ̸= 0 , se le llama ecuación
de segundo grado. Los valores que satisfacen la ecuación se llaman raíces o soluciones de la
ecuación.
Solución gráfica de una ecuación de segundo grado.
Considerando la ecuación general de segundo grado
ax 2 + bx + c = 0
la gráfica de esta ecuación es invariablemente una parábola, que abre hacia arriba si el coeficiente a es positiva y abre hacia abajo en el caso que a sea negativa. Las raíces de la ecuación
corresponden a los valores de la variable x donde la gráfica cruza el propio eje X .
En algunos casos la gráfica queda completamente por arriba o por abajo del eje X . En estos
casos decimos que la ecuación no tiene solución real. Si se resolviera por fórmula general se
tendría la raíz de un número negativo.
5x 2 − 3x + 6
−2x 2 + 4x − 3
x 2 − 2x − 24
Solución algebraica de una ecuación de segundo grado.
Existen diversos métodos para obtener las soluciones de una ecuación de segundo grado, entre
los que destaca la fórmula general que se define por:
p
−b ± b 2 − 4ac
x=
2a
Con esta fórmula se resuelve cualquier tipo de ecuación de segundo grado, además está el método por factorización.
Fórmula general.
Para aplicar la fórmula general se deben obtener los valores de a, b y c en el orden de la ecuación de segundo grado a 2 + bx + c = 0, donde:
a: coeficiente del término cuadrático.
b: coeficiente del término lineal.
c: término independiente.
- En la ecuación de la forma ax 2 + bx = 0, se sustituye c = 0.
- En la ecuación de la forma ax 2 + c = 0, se sustituye b = 0.
1.38
Ecuación de segundo grado
Las raíces de la ecuación x 2 + 4x + 3 = 0 son:
a) 1, 3
b) −1, −3
c) 1, −3
d) −1, 3
Solución .
Se obtienen los valores de a, b y c de la ecuación:
a = 1, b = 4 y c = 3
Estos valores se sustituyen en la fórmula general:
x=
=
=
=
p
(4)2 − 4(1)(3)
2(1)
p
−4 ± 16 − 12
2
p
−4 ± 4
2
−4 ± 2
2
−(4) ±
Se calcula para cuando es +2 y para cuando es −2, de forma independiente
x1 =
−4 + 2 −2
=
= −1;
2
2
x2 =
−4 − 2 −6
=
= −3
2
2
Por consiguiente, las raíces son: x 1 = −1 y x 2 = −3 y la opción correcta está en el inciso b.
Sistemas de ecuaciones lineales con dos incógnitas
Se les denomina sistemas de ecuaciones a aquellas que se satisfacen para valores iguales de las
incógnitas.
Método de reducción para resolver un sistema de ecuaciones
Consiste en sumar ambas ecuaciones y eliminar una de las variables, así se obtiene una ecuación de primer grado con una incógnita.
1.39
Sistema de ecuaciones
El valor de x y y que satisface el sistema
2x + 5y = 7
3x + 2y = 5
es:
a)x = 1, y = −1
c) x = 1, y = 1
b) x = −1, y = 1
d) x = −1, y = −1
Solución .
Se elige una incógnita a eliminar, en este caso x, por tanto, los coeficientes deben ser
iguales, pero de signo contrario, entonces la primera ecuación se multiplica por el coeficiente de x de la segunda ecuación, y la segunda ecuación se multiplica por el coeficiente
de x de la primera ecuación de signo contrario.
3(2x + 5y = 7)
−→
6x + 15y = 21
−2(3x + 2y = 5)
−→
−6x − 4y = −10
Las ecuaciones resultantes se suman:
6x + 15y = 21
− 6x − 4y = −10
11y = 11
De la ecuación resultante, se despeja y
11
11
y =1
y=
El valor de y = 1 se sustituye en cualquiera de las ecuaciones iniciales, en este caso se
elige la ecuación 2x + 5y = 7 para determinar x, entonces:
2x + 5y = 7
−→
2x + 5(1) = 7
−→
2x + 5 = 7
−→
2x = 7 − 5
−→
2x = 2
2
x=
2
x =1
−→
−→
La solución del sistema es x = 1, y = 1, por tanto, la opción correcta es el inciso c.
Método de sustitución
Consiste en despejar una incógnita de cualquiera de ambas ecuaciones para sustituir en la
ecuación restante y obtener una ecuación de primer grado con una incógnita.
1.40
Método de sustitución
¿Cuáles son los valores que satisfacen el sistema siguiente 5a + 2b = −5?
a) a = 3, b = 5
b) a = 3, b = −5
c) a = −3, b = −5
b=5
d) a = −3,
Solución .
Se despeja una incógnita de cualquiera de las ecuaciones, en este caso a, de la primera
ecuación.
5a + 2b = −5
−→
5a = −5 − 2b
−→
a=
−5 − 2b
5
El despeje que se obtiene se sustituye en la segunda ecuación.
µ
7a + 3b = −6
7
−→
La nueva ecuación se resuelve.
¶
µ
−5 − 2b
+ 3b = −6
7
5
¶
−5 − 2b
+ 3b = −6
5
µ
−→
¶
−35 − 14b
+ 3b = −6
5
−35 − 14b
= −6 − 3b
5
−35 − 14b = −30 − 15b
−→
−14b + 15b = −30 + 35
−→
b=5
−→
−→
El valor de b = 5 se sustituye en el despeje de a.
−5 − 2b
5
−5 − 2(5)
=
5
−5 − 10
=
5
−15
=
5
= −3
a=
Los valores que satisfacen el sistema son: a = −3 y b = 5
Por tanto, la opción correcta es el inciso d.
Método gráfico
Cada una de las ecuaciones que forman al sistema
a1 x + b1 = c1
a2 x + b2 y = c2
tiene una representación en el plano cartesiano, éstas son rectas que se intersecan en un punto,
al cual se le llama solución del sistema de ecuaciones.
Problemas sobre sistemas de ecuaciones lineales
1.41
Problemas
Hallar dos números cuya suma sea 27 y que el séxtuplo del menor supere en 9 unidades
al triple del mayor.
a) a = 10, b = 17
b) a = 13, b = −15
c) a = 12, b = 8
d) a = 13,
b = 14
Solución .
Número menor = x
Número mayor = 27 − x
6x = 3(27 − x) + 9
6x = 81 − 3x + 9
6x = 90
x = 10
Número menor=10 y número mayor = 27 - 10 = 17
Sistemas de 3 ecuaciones lineales
Un sistema de ecuaciones lineales con 3 incógnitas, consiste en 3 ecuaciones con 3 variables
de grado 1, la forma estándar de este tipo de sistemas es:
a1 x1 + a2 x2 + a3 x3 = d1
b1 x1 + b2 x2 + b3 x3 = d2
c1 x1 + c2 x2 + c3 x3 = d3
A los valores x 1 , x 2 y x 3 que satisfacen las 3 ecuaciones se le llama solución del sistema de
ecuaciones. Al igual que en el sistema de 2 por 2, se conocen diferentes métodos de encontrar
su solución; sustitución, igualación, determinantes y otros, en este caso sólo se abordará el
método de suma y resta, aunque se debe aclarar que todos los métodos son iguales al caso de
2 ecuaciones, sólo se realiza una generalización.
Método de suma y resta
Es quizás uno de los métodos más usados para resolver sistemas de ecuaciones. Es recomendable usar este método cuando se tienen dos ecuaciones completas, es decir, todos los coeficientes son distintos de cero. Los pasos para resolver un sistema de 3 ecuaciones por este método
son:
1.Se identifica una variable a eliminar, puede ser de manera arbitraria pero es importante
trabajar sobre esta variable en los 3 siguientes pasos.
2. Se seleccionan 2 ecuaciones y se multiplican los coeficientes de la variable a eliminar de forma cruzada, es decir, el coeficiente en la primera ecuación se multiplica por la segunda
y viceversa, cuidándose que queden con signos contrarios.
3. Se realiza la suma de las ecuaciones, la ecuación resultante se renombra como ecuación 4
(se reduce a una ecuación con 2 incógnitas.)
4.Se seleccionan otras 2 ecuaciones y se repiten los 2 pasos anteriores, la ecuación resultante
se renombra como ecuación 5 (se reduce a una ecuación con 2 incógnitas con las mismas
variables de la anterior).
5. Se forma el sistema de ecuaciones de 2 por 2 con las ecuaciones 4 y 5 y se resuelve.
6. Se sustituyen los dos valores encontrados en el paso anterior, en cualquiera de las 3 ecuaciones originales y se resuelve para encontrar el tercer valor.
1.42
Método de suma y resta
Resolver el siguiente sistema de ecuaciones por el método de sumas y restas:
x + 4y − z = 6
2x + 5y − 7z = −9
3x − 2y − z = 6
Solución .
Se selecciona la variable x para trabajar, luego se numera el sistema y se escogen las
ecuaciones 1 y 2.
Ec.1)
x + 4y − z = 6
Ec.2)
2x + 5y − 7z = −9
Ec.3)
3x − 2y − z = 6
Se multiplica por −2 la primera ecuación y por 1 la segunda.
−2x − 8y + 2z = −12
2x + 5y − 7z = −9
Al sumar se obtiene −3y − 5z = −21 que se nombra ecuación 4. Ahora se trabaja con la
ecuación 1 que se multiplica por −3 y con la ecuación 3 que se multiplica por 1.
−3x − 12y + 3z = −18
3x − 2y + z = 2
Al sumar se obtiene −14y +4z = −16 que se nombra ecuación 5. Se forma un sistema con
las ecuaciones 4 y 5.
Ec.4)
−3y − 5z = −21
Ec.5)
−14y + 4z = −16
Que al resolver se obtiene y = 2 y z = 3, estos valores se sustituyen en la ecuación 1 y se
resuelve para concluir.
x + 4(2) − (3) = 6
−→
x = 6−8+3
−→
x =1
Representaciones gráficas
Una relación consta de todos los pares ordenados (x, y) que se generan de la correspondencia
que existe entre 2 conjuntos.
Una función es la relación que existe entre 2 conjuntos, de tal manera que a cada elemento del
conjunto origen le corresponde un solo elemento del conjunto destino, mediante una regla de
correspondencia.
Se representa como:
y = f (x) se lee: la variable y está en función de x.
Identificación de una función y una relación a partir de su gráfica.
Se trazan rectas paralelas al eje Y , si la recta corta en un punto a la curva, entonces la gráfica
representa una función, en caso de que la recta corte en 2 o más puntos a la curva, la gráfica
representa una relación.
1.43
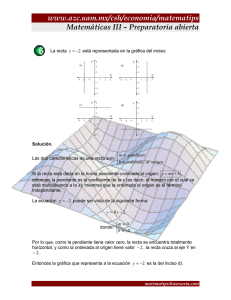
La siguiente gráfica representa una función:
Solución .
Porque al trazar la recta paralela al eje Y , ésta corta en un solo punto a la curva.
1.44
La siguiente gráfica representa una relación.
Solución .
Porque al trazar la recta paralela al eje Y , ésta corta en 2 puntos a la curva.
Tipos de funciones y sus gráficas.
Existen diversos tipos de funciones entre las que destacan las siguientes.
Función constante. Es de la forma f (x) = c, donde c es una constante y representa la distancia
al eje X , su gráfica es una recta paralela al eje X .
Función lineal. Es de la forma f (x) = ax + b y su gráfica representa una línea inclinada.
Si a > 0, su ángulo de inclinación θ es mayor que 0°, pero menor que 90°.
Si a < 0, su ángulo de inclinación θ es mayor que 90°, pero menor que 180°.
Función cuadrática. Es de la forma f (x) = ax 2 + bx + c y su gráfica representa una parábola
vertical.
Si a > 0, la parábola abre hacia arriba (cóncava hacia arriba).
Si a < 0, la parábola abre hacia abajo (cóncava hacia abajo).
Función cúbica. Es de la forma f (x) = ax 3 + bx 2 + c x + d y sus diferentes gráficas son de la
forma:
Si f (x) = ax 3 , entonces:
Con a > 0:
Con a < 0:
Si f (x) = ax 3 + bx 2 + cx + d , entonces
Con a > 0
Con a < 0
Función exponencial. Es de la forma f (x) = a x y su gráfica es:
Si 0 < a < 1
Si a > 1
Función logarítmica Es de la forma f (x) = l og a x, con x > 0 y su gráfica es:
1.45
Función exponencial
¿Cuál de las siguientes funciones es una función exponencial?
a) f (x) = 3 b) f (x) = 2x c) f (x) = 3x + 2 d) f (x) = x 2 + 5x + 6
Solución .
En una función exponencial la variable x se encuentra como exponente, por tanto, la
opción correcta es el inciso b.
1.5
1.5.1
Razonamiento Estadístico y probabilístico
Frecuencias e información gráfica
Las gráficas de barras y diagramas de sectores se emplean para representar distribuciones de
frecuencias (número de veces que se repite un dato o cifra), en atención de un atributo o carácter cualitativo.
1.46
Diagrama de sectores
Con base en la siguiente información, traza un diagrama de sectores. En una encuesta
sobre el grado de escolaridad, hecha a un grupo de 200 personas, los datos obtenidos
son:
Clave
PU
PM
PE
PSL
PNL
Característica
(grado de escolaridad)
Personas con estudios universitarios(superior)
Personas con estudios de preparatoria (medio superior)
Personas con estudios elementales (primaria y secundaria)
Personas que únicamente saben leer
Personas que no saben leer
Total
Número de personas
(frecuencia)
20
35
80
60
5
200
Solución .
Para realizar el diagrama de sectores se dividen los 360◦ del círculo, de forma proporcional a las frecuencias de los distintos valores de las variables
Grados en circunferencia → 360◦ 36◦ 63◦ 144◦ 108◦ 9◦
=
=
=
=
=
Número de personas → 200
20
35
80
60
5
El diagrama de sectores es:
1.47
Diagrama de sectores
Con base en el diagrama de sectores circular del Ejemplo 1.46, ¿cuál de las siguientes
afirmaciones es correcta?
a) El número de universitarios es mayor que el número de personas que únicamente
saben leer.
b) El número de personas con estudios elementales es menor que el número de per-
sonas con estudios universitarios.
c) El número de personas que únicamente saben leer, es mayor que el número de
personas que no saben leer.
d) El número de personas que no saben leer es el mismo que el de personas con estudios universitarios.
e) El número de personas que no saben leer es el mismo que el de personas con estudios elementales.
Solución .
La interpretación del diagrama de sectores es la herramienta para indicar cuál de las
afirmaciones es la correcta, en este caso la respuesta es el inciso c.
Gráficas de barras.
Para elaborar una gráfica de barras es necesario trazar un plano cartesiano: en el eje de las
abscisas (x) se ponen los diversos datos o características de los mismos; en el eje de las ordenadas (y) se pone el número de personas u objetos que cumplen con determinada característica
(frecuencia). Los diagramas de barras también se trazan en forma horizontal, por tanto, la información en los ejes ordenados se invertirá.
1.48
Gráfica de barras
Con base en la información del Ejemplo 1.46 del diagrama de sectores, traza una gráfica
de barras.
Solución .
Al trazar la gráfica de barras se levantan rectángulos de igual base sobre cada una de las
variables. En este caso es el grado de escolaridad que un grupo de 200 personas tiene;
la altura que tendrá cada rectángulo es el número de personas que tiene cada grupo, el
valor de cada variable; a este número se le conoce como frecuencia.
Es importante mencionar que en este caso se emplea una escala en el eje de las ordenadas, la cual es 1:5 personas.
1.49
Gráfica de barras
Con base en el diagrama de barras, ¿cuál de las siguientes afirmaciones NO es correcta?
a) El número de personas con estudios universitarios es mayor que el número de
personas que no tienen estudios y no saben leer.
b) El número de personas con estudios de preparatoria es menor que el número de
personas con estudios universitarios.
c) El número de personas sin estudios, pero que saben leer, es mayor que el número
de personas que no tienen estudios y no saben leer.
d) El número de personas con estudios elementales es mayor que la suma de personas que no tienen estudios pero saben y las que no saben leer.
e) El número de personas con estudios elementales es igual que la suma de personas
que no tienen estudios pero saben y las que no saben leer.
Solución .
La respuesta correcta corresponde al inciso b, ya que el número de personas con estudios
de preparatoria es mayor que el número de personas con estudios universitarios.
Polígono de frecuencias.
El polígono de frecuencias se obtiene al unir los puntos medios colocados en la cara superior
de cada rectángulo de un histograma.
1.50
Polígono de frecuencias
El polígono de frecuencias del ejemplo anterior es:
Solución .
Realizamos la grafica de barras y vamos uniendo cada uno de sus puntos medios como
se indica
1.51
Polígono de frecuencias
La casa editorial El arbolito dio a conocer la venta de libros por mes, del primer semestre
del año 2005, y los resultados fueron los siguientes:
Con los datos anteriores, realiza el histograma y traza el polígono de frecuencias.
Solución .
Realizamos la grafica de barras de acuerdo a los datos proporcionados
Los rectángulos trazados con líneas punteadas representan al histograma, mientras que
la línea continua representa al polígono de frecuencias.
1.5.2
Medidas descriptivas
Medidas de tendencia central
Son las cantidades que indican la tendencia de los datos a agruparse en torno a una cantidad
central y se clasifican de la siguiente manera:


 Media aritmética (promedio)
Medidas de tendencia central Mediana


Moda
Media aritmética. Se define como el promedio de los datos : x 1 , x 2 , x 3 , . . . , x n y se representa por
X.
x1 + x2 + x3 + · · · + xn
X=
n
1.52
Media aritmética
¿Cuál es la media aritmética de los siguientes datos: 5, 7, 3, 5, 4, 4, 8, 5, 3?
a) 4
Solución .
b)4.8
c) 5
d ) 5.2
e ) 5.4
De acuerdo a la fórmula anterior
X=
5+7+3+5+4+4+8+5+3
= 4.8
9
Por tanto, la opción correcta es el inciso b.
Mediana. Al ordenar los datos de forma creciente o decreciente, al valor que se encuentra exactamente a la mitad se le denomina mediana.
1.53
Mediana
Las calificaciones en matemáticas de un grupo de 25 alumnos son:
9, 8, 9, 6, 7, 5, 8, 4, 5, 7, 6, 6, 5, 4, 9, 9, 8, 6, 7, 8, 8, 3, 10, 8, 9
De acuerdo con los datos anteriores, ¿cuál es la mediana?
a) 8
b) 10
c) 5
d)7
e)9
Solución .
La mediana es aquel valor que se encuentra exactamente a la mitad, o que tiene el mismo
número de datos a su izquierda que a su derecha, entonces
Por tanto, la opción correcta es el inciso d.
1.54
Mediana
Las estaturas en metros de un grupo de personas son las siguientes:
1.65, 1.72, 1.68, 1.58, 1.70, 1.71, 1.68, 1.69, 1.65, 1.66, 1.76, 1.74
De acuerdo con los datos anteriores, ¿cuál es la mediana?
a) 1.675
b) 1.68
c) 1.685
d ) 1.69
e ) 1.7
Solución .
Se acomodan los datos en forma ascendente (de menor a mayor).
1.58, 1.65, 1.65, 1.66, 1.68, 1.68, 1.69, 1.70, 1.71, 1.72, 1.74, 1.76
El número de datos es par, entonces los elementos que están exactamente a la mitad son
1.68 y 1.69, por consiguiente la mediana es el promedio de ambos valores
1.68 + 1.69
= 1.685
2
Por tanto, la opción correcta es el inciso c.
Moda. Es el dato que tiene la mayor frecuencia, el que más se repite. Una serie de datos puede
tener más de una moda, por lo que tendría una distribución multimodal.
1.55
Mediana
El sueldo promedio semanal de una serie de empleados gubernamentales es:
$1200, $1100, $2000, $1800, $1500, $1100,
$1200, $1650, $1200, $2000, $1600, $1200
De acuerdo con los datos anteriores, ¿cuál es la moda?
a) $1100
b) $2000
c) $1650
d ) $1200
e ) $1500
Solución .
De acuerdo a la definición, el valor que más se repite es $1200, por tanto, la opción correcta es el inciso d.
1.5.3
Medidas de dispersión
Son las que permiten indicar la distancia de los valores de la variable a un cierto valor central,
o que identifican la concentración de los datos en un cierto sector del recorrido de la variable.
Algunas de las medidas de dispersión más usuales son:
a) Rango, amplitud o recorrido
b) Desviación estándar
c) Varianza
Rango. Se denomina rango a la diferencia entre el dato mayor y el dato menor.
R = x máx − x mín
Desviación estándar. Se define como la raíz cuadrada de los cuadrados de las desviaciones de
los valores de la variable, respecto a su media.
s ¡
¢2
P
x −x
S=
n
Varianza. Se define como el cuadrado de la desviación estándar (S 2 ).
1.56
Rango, desviación estándar y varianza
Las edades de los alumnos asistentes al curso de ajedrez son:
20, 17, 20, 21, 16, 18, 19, 17, 18, 20, 19, 21, 18, 17, 19, 21, 22, 18, 24 y 19
Determinar el rango, la desviación estándar y la varianza.
a) 8, 1.91, 3.66
b) 6, 3.5, 12.25
Solución .
El rango se define como:
c) 8, 1.5, 2.25
d ) 6, 1.8, 3.24
e ) 8, 1.9, 3.25
x máx − x mín = 24 − 16 = 8
Para obtener la desviación estándar y varianza se obtiene la media aritmética
x=
Suma de los datos 384
=
= 19.2
Número de datos
20
y se aplican las fórmulas respectivas
x −x
20 - 19.2
17 - 19.2
20 - 19.2
21 - 19.2
16 - 19.2
18 - 19.2
19 - 19.2
17 - 19.2
18 - 19.2
20 - 19.2
19 - 19.2
21 - 19.2
18 - 19.2
17 - 19.2
19 - 19.2
21 - 19.2
22 - 19.2
18 - 19.2
24 - 19.2
19 - 19.2
0.8
- 2.2
0.8
1.8
- 3.2
- 1.2
- 0.2
- 2.2
- 1.2
0.8
- 0.2
1.8
- 1.2
- 2.2
- 0.2
1.8
2.8
- 1.2
4.8
- 0.2
(x − x)2
0.64
4.84
0.64
3.24
10.24
1.44
0.04
4.84
1.44
0.64
0.04
3.24
1.44
4.84
0.04
3.24
7.84
1.44
23.04
0.04
P
(x − x)2 = 73.2
P
(x − x)2 73.2
=
= 3.66
n
20
sP
(x − x)2 p
= 3.66 = 1.91
n
Varianza
Desviación estándar
Por tanto, la opción correcta es el inciso a.
1.5.4
Medidas de posición
Las medidas de posición son cantidades que dividen una colección ordenada de datos, en 4, 10
o 100 partes iguales.
Cuartiles
Los cuartiles son 3 números que dividen a la colección ordenada de datos en 4 partes iguales.
Sus valores pueden ser datos, o bien cantidades obtenidas al promediar dos datos consecutivos
de la colección ordenada. Cuartil 1 (Q 1 ): es un número tal que el 25 % de los datos son menores
o iguales a él y el 75 % de los datos son mayores o iguales a él. Su posición en la colección
ordenada se obtiene dividiendo el total de datos (n) entre 4.
Cuartil 2 (Q 2 ): coincide con la mediana porque es una cantidad tal que el 50 % de los datos son
menores o iguales a ella y el otro 50 % son mayores o iguales.
Cuartil 3 (Q 3 ): es un número tal que el 75 % de los datos son menores o iguales a él y el 25 % son
mayores o iguales. Su posición en la colección ordenada se obtiene multiplicando el total de
datos (n) por 34.
1.57
Cuartiles
Se tomó el tiempo (en minutos) que tardaron 16 niños en resolver un test psicológico.
Estos son los datos:
28, 20, 21, 20, 23, 25, 26, 19, 29, 22, 18, 30, 26, 29, 24, 25
Encontrar los cuartiles Q 1 ,Q 2 ,Q 3 .
a) Q 1 = 18, Q 2 = 25 y Q 3 = 30.
b) Q 1 = 20, Q 2 = 25 y Q 3 = 27.
c) Q 1 = 20.5, Q 2 = 24.5 y Q 3 = 27.
d) Q 1 = 28, Q 2 = 29 y Q 3 = 25.
e) Q 1 = 21, Q 2 = 25 y Q 3 = 29.
Solución .
Datos ordenados:
18, 19, 20, 20, 21, 22, 23, 24, 25, 25, 26, 26, 28, 29, 29, 30
Cuartil
Q1
Q2
Q3
Posición
1
4 (16) = 4, promedio 4° y 5°
2
4 (16) = 8, promedio 8° y 9°
3
4 (16) = 12, promedio 12° y 13°
Valor
20.5
24.5
27
Así que los cuartiles son: Q 1 = 20.5, Q 2 = 24.5 y Q 3 = 27.
Por tanto, la opción correcta es el inciso c.
1.58
Cuartiles
Las notas obtenidas por 21 estudiantes en un examen de matemáticas, son:
8.5, 10, 7, 7.5, 6, 5, 6.5, 8.5, 9, 7.5, 8, 10, 9.5, 9, 4, 5.5, 6, 7.5, 7, 7.5, 8
Encontrar los cuartiles Q 1 ,Q 2 ,Q 3 .
a) Q 1 = 5.5, Q 2 = 7.5 y Q 3 = 9.5.
b) Q 1 = 7.5, Q 2 = 8.5 y Q 3 = 9.5.
c) Q 1 = 7, Q 2 = 8 y Q 3 = 9.
d) Q 1 = 6, Q 2 = 7 y Q 3 = 8.
e) Q 1 = 6.5, Q 2 = 7.5 y Q 3 = 8.5.
Solución .
Datos ordenados:
4, 5, 5.5, 6, 6, 6.5, 7, 7, 7.5, 7.5, 7.5, 7.5, 8, 8, 8.5, 8.5, 9, 9, 9.5, 10, 10
Cuartil
Q1
Q2
Q3
Posición
1
4 (21) = 5.25, 6° lugar
2
4 (21) = 10.5, 11° lugar
3
4 (21) = 15.75, 16° lugar
Valor
6.5
7.5
8.5
Así que los cuartiles son: Q 1 = 6.5, Q 2 = 7.5 y Q 3 = 8.5.
Por tanto, la opción correcta es el inciso e.
Deciles
Se trata de 9 números que dividen a la colección ordenada de datos en 10 partes iguales. Se
denotan por D 1 , D 2 , D 3 , . . . , D 9 . Estas medidas se usan cuando la cantidad de datos es grande.
Sus valores se calculan de manera similar a la forma en que se calcularon los cuartiles.
El 10 % de los datos son menores o iguales que D 1 y el 90 % mayores o iguales.
El 20 % de los datos son menores o iguales que D 2 y el 80 % mayores o iguales.
El 30 % de los datos son menores o iguales que D 3 y el 70 % mayores o iguales. Y así sucesivamente.
Percentiles
Son 99 números que dividen a la colección ordenada de datos en 100 partes iguales. Se denotan
por P 1 , P 2 , P 3 , . . . , P 99 . Estos permiten determinar rangos de variación de cualquier porcentaje
de los datos. Por ejemplo, el 22 % de los datos son menores o iguales a P 22 y el 78 % son mayores
o iguales. El 65 % de los datos son menores o iguales que P 65 y el 35 % es mayor o igual.
1.5.5
Nociones de probabilidad
Existen dos tipos de eventos
Determinísticos.
Estocásticos o probabilísticos.
Si se arroja una moneda al aire es evidente que, por efecto de la gravedad, la moneda cae. Dicho
evento es invariable, por eso es un evento determinístico.
Al arrojar la moneda al aire, se da por hecho que caerá, lo que se desconoce es si la cara de la
moneda será sol o águila, por tanto, se trata de un evento estocástico o probabilístico.
El número total de eventos es también conocido como espacio muestral. En esta lección se
estudiaran únicamente los eventos probabilísticos. La probabilidad se define:
P (x) =
Número de casos favorables
Número total de casos
donde x es el evento estocástico o probabilístico.
1.59
Probabilidad
Al lanzar una moneda, ¿cuál es la probabilidad de obtener águila?
a) 100 %
b) 75 %
c) 50 %
d ) 25 %
e ) 65 %
Solución .
Evento probabilístico (x = lanzar la moneda).
P (x) =
Número de casos favorables
Número total de casos
Número de casos favorables = 1
Número total de casos = 2
(sólo una cara de la moneda es águila)
(número de caras en una moneda)
1
P (x) =
2
La probabilidad se expresa en fracción común 12 , fracción decimal 0.5, o como porcentaje
50 %.
Por tanto, la opción correcta es el inciso c.
1.60
Probabilidad
Al lanzar un dado, ¿qué probabilidad existe de obtener un número menor o igual que 4?
a) 0.25
b) 0.333...
c) 0.444...
d ) 0.666...
e ) 0.5
Solución .
Evento probabilístico (x = lanzar el dado).
P (x) =
Número de casos favorables
Número total de casos
Número de casos favorables = 4
Número total de casos = 6
(caras posibles, 1, 2, 3 y 4)
(número de caras en un dado)
4 2
P (x) = = = 0.666...
6 3
Por tanto, la opción correcta es el inciso d.
1.61
Probabilidad
En una urna hay 6 esferas rojas, 2 azules y 2 verdes. ¿Cuántas esferas hay que sacar, para
tener la certeza de tener 2 esferas azules?
a) 10
b) 8
c) 4
d)2
e)6
Solución .
Sacar una esfera de la urna es un evento estocástico, por tanto, la primera esfera puede
ser roja, verde o azul. Entonces para tener la certeza de que se tengan 2 esferas azules,
se deben de extraer la suma del número de esferas de los demás colores y el número de
esferas del color que se desea.
6 esferas rojas + 2 esferas verdes + 2 esferas azules = 10 esferas.
Por tanto, la opción correcta es el inciso a.
1.62
Probabilidad
En un grupo de 20 personas, 3 cuartas partes saben nadar, de las cuales una tercera parte
son mujeres. ¿Cuál es la probabilidad de que al escoger a un representante del grupo,
dicha persona sea una mujer que sepa nadar?
a) 0.10
b) 0.25
c) 0.5
d ) 0.75
e ) 0.333...
Solución .
Las tres cuartas partes del grupo son las personas que saben nadar.
µ ¶
3
(20) = 15 personas que saben nadar.
4
µ ¶
1
(15) = 5 mujeres que saben nadar.
3
Evento probabilístico (x = escoger una persona).
P (x) =
Número de casos favorables
Número total de casos
Número de casos favorables = 5
Número total de casos = 20
(personas que son mujeres y saben nadar)
(número total de personas del grupo)
1
5
= = 0.25
P (x) =
20 4
Por tanto, la opción correcta es el inciso b.
1.63
Probabilidad
En una bolsa hay 15 golosinas de vainilla, 10 de café y 5 de chocolate. ¿Qué probabilidad
existe de sacar una golosina que NO sea de chocolate?
a) 83.3 %
b) 66.6 %
c) 50 %
d ) 16.6 %
e ) 75 %
Solución .
Evento probabilístico (x = sacar una golosina).
Número de casos favorables = 25
Número total de casos = 30
(número de golosinas que NO son de chocolate)
(número total de golosinas)
25 5
P (x) =
= = 0.833 = 83.3 %
30 6
Por tanto, la opción correcta es el inciso a.
1.6
1.6.1
Razonamiento Estadístico y probabilístico
Frecuencias e información gráfica
Las gráficas de barras y diagramas de sectores se emplean para representar distribuciones de
frecuencias (número de veces que se repite un dato o cifra), en atención de un atributo o carácter cualitativo.
1.64
Diagrama de sectores
Con base en la siguiente información, traza un diagrama de sectores. En una encuesta
sobre el grado de escolaridad, hecha a un grupo de 200 personas, los datos obtenidos
son:
Clave
PU
PM
PE
PSL
PNL
Característica
(grado de escolaridad)
Personas con estudios universitarios(superior)
Personas con estudios de preparatoria (medio superior)
Personas con estudios elementales (primaria y secundaria)
Personas que únicamente saben leer
Personas que no saben leer
Total
Número de personas
(frecuencia)
20
35
80
60
5
200
Solución .
Para realizar el diagrama de sectores se dividen los 360◦ del círculo, de forma proporcional a las frecuencias de los distintos valores de las variables
Grados en circunferencia → 360◦ 36◦ 63◦ 144◦ 108◦ 9◦
=
=
=
=
=
Número de personas → 200
20
35
80
60
5
El diagrama de sectores es:
1.65
Diagrama de sectores
Con base en el diagrama de sectores circular del Ejemplo 1.46, ¿cuál de las siguientes
afirmaciones es correcta?
a) El número de universitarios es mayor que el número de personas que únicamente
saben leer.
b) El número de personas con estudios elementales es menor que el número de personas con estudios universitarios.
c) El número de personas que únicamente saben leer, es mayor que el número de
personas que no saben leer.
d) El número de personas que no saben leer es el mismo que el de personas con estudios universitarios.
e) El número de personas que no saben leer es el mismo que el de personas con estudios elementales.
Solución .
La interpretación del diagrama de sectores es la herramienta para indicar cuál de las
afirmaciones es la correcta, en este caso la respuesta es el inciso c.
Gráficas de barras.
Para elaborar una gráfica de barras es necesario trazar un plano cartesiano: en el eje de las
abscisas (x) se ponen los diversos datos o características de los mismos; en el eje de las ordenadas (y) se pone el número de personas u objetos que cumplen con determinada característica
(frecuencia). Los diagramas de barras también se trazan en forma horizontal, por tanto, la información en los ejes ordenados se invertirá.
1.66
Gráfica de barras
Con base en la información del Ejemplo 1.46 del diagrama de sectores, traza una gráfica
de barras.
Solución .
Al trazar la gráfica de barras se levantan rectángulos de igual base sobre cada una de las
variables. En este caso es el grado de escolaridad que un grupo de 200 personas tiene;
la altura que tendrá cada rectángulo es el número de personas que tiene cada grupo, el
valor de cada variable; a este número se le conoce como frecuencia.
Es importante mencionar que en este caso se emplea una escala en el eje de las ordenadas, la cual es 1:5 personas.
1.67
Gráfica de barras
Con base en el diagrama de barras, ¿cuál de las siguientes afirmaciones NO es correcta?
a) El número de personas con estudios universitarios es mayor que el número de
personas que no tienen estudios y no saben leer.
b) El número de personas con estudios de preparatoria es menor que el número de
personas con estudios universitarios.
c) El número de personas sin estudios, pero que saben leer, es mayor que el número
de personas que no tienen estudios y no saben leer.
d) El número de personas con estudios elementales es mayor que la suma de personas que no tienen estudios pero saben y las que no saben leer.
e) El número de personas con estudios elementales es igual que la suma de personas
que no tienen estudios pero saben y las que no saben leer.
Solución .
La respuesta correcta corresponde al inciso b, ya que el número de personas con estudios
de preparatoria es mayor que el número de personas con estudios universitarios.
Polígono de frecuencias.
El polígono de frecuencias se obtiene al unir los puntos medios colocados en la cara superior
de cada rectángulo de un histograma.
1.68
Polígono de frecuencias
El polígono de frecuencias del ejemplo anterior es:
Solución .
Realizamos la grafica de barras y vamos uniendo cada uno de sus puntos medios como
se indica
1.69
Polígono de frecuencias
La casa editorial El arbolito dio a conocer la venta de libros por mes, del primer semestre
del año 2005, y los resultados fueron los siguientes:
Con los datos anteriores, realiza el histograma y traza el polígono de frecuencias.
Solución .
Realizamos la grafica de barras de acuerdo a los datos proporcionados
Los rectángulos trazados con líneas punteadas representan al histograma, mientras que
la línea continua representa al polígono de frecuencias.
1.6.2
Medidas descriptivas
Medidas de tendencia central
Son las cantidades que indican la tendencia de los datos a agruparse en torno a una cantidad
central y se clasifican de la siguiente manera:


 Media aritmética (promedio)
Medidas de tendencia central Mediana


Moda
Media aritmética. Se define como el promedio de los datos : x 1 , x 2 , x 3 , . . . , x n y se representa por
X.
x1 + x2 + x3 + · · · + xn
X=
n
1.70
Media aritmética
¿Cuál es la media aritmética de los siguientes datos: 5, 7, 3, 5, 4, 4, 8, 5, 3?
a) 4
b)4.8
c) 5
d ) 5.2
e ) 5.4
Solución .
De acuerdo a la fórmula anterior
X=
5+7+3+5+4+4+8+5+3
= 4.8
9
Por tanto, la opción correcta es el inciso b.
Mediana. Al ordenar los datos de forma creciente o decreciente, al valor que se encuentra exactamente a la mitad se le denomina mediana.
1.71
Mediana
Las calificaciones en matemáticas de un grupo de 25 alumnos son:
9, 8, 9, 6, 7, 5, 8, 4, 5, 7, 6, 6, 5, 4, 9, 9, 8, 6, 7, 8, 8, 3, 10, 8, 9
De acuerdo con los datos anteriores, ¿cuál es la mediana?
a) 8
b) 10
c) 5
d)7
e)9
Solución .
La mediana es aquel valor que se encuentra exactamente a la mitad, o que tiene el mismo
número de datos a su izquierda que a su derecha, entonces
Por tanto, la opción correcta es el inciso d.
1.72
Mediana
Las estaturas en metros de un grupo de personas son las siguientes:
1.65, 1.72, 1.68, 1.58, 1.70, 1.71, 1.68, 1.69, 1.65, 1.66, 1.76, 1.74
De acuerdo con los datos anteriores, ¿cuál es la mediana?
a) 1.675
b) 1.68
c) 1.685
d ) 1.69
e ) 1.7
Solución .
Se acomodan los datos en forma ascendente (de menor a mayor).
1.58, 1.65, 1.65, 1.66, 1.68, 1.68, 1.69, 1.70, 1.71, 1.72, 1.74, 1.76
El número de datos es par, entonces los elementos que están exactamente a la mitad son
1.68 y 1.69, por consiguiente la mediana es el promedio de ambos valores
1.68 + 1.69
= 1.685
2
Por tanto, la opción correcta es el inciso c.
Moda. Es el dato que tiene la mayor frecuencia, el que más se repite. Una serie de datos puede
tener más de una moda, por lo que tendría una distribución multimodal.
1.73
Mediana
El sueldo promedio semanal de una serie de empleados gubernamentales es:
$1200, $1100, $2000, $1800, $1500, $1100,
$1200, $1650, $1200, $2000, $1600, $1200
De acuerdo con los datos anteriores, ¿cuál es la moda?
a) $1100
b) $2000
c) $1650
d ) $1200
e ) $1500
Solución .
De acuerdo a la definición, el valor que más se repite es $1200, por tanto, la opción correcta es el inciso d.
1.6.3
Medidas de dispersión
Son las que permiten indicar la distancia de los valores de la variable a un cierto valor central,
o que identifican la concentración de los datos en un cierto sector del recorrido de la variable.
Algunas de las medidas de dispersión más usuales son:
a) Rango, amplitud o recorrido
b) Desviación estándar
c) Varianza
Rango. Se denomina rango a la diferencia entre el dato mayor y el dato menor.
R = x máx − x mín
Desviación estándar. Se define como la raíz cuadrada de los cuadrados de las desviaciones de
los valores de la variable, respecto a su media.
s
S=
P¡
x −x
¢2
n
Varianza. Se define como el cuadrado de la desviación estándar (S 2 ).
1.74
Rango, desviación estándar y varianza
Las edades de los alumnos asistentes al curso de ajedrez son:
20, 17, 20, 21, 16, 18, 19, 17, 18, 20, 19, 21, 18, 17, 19, 21, 22, 18, 24 y 19
Determinar el rango, la desviación estándar y la varianza.
a) 8, 1.91, 3.66
b) 6, 3.5, 12.25
c) 8, 1.5, 2.25
d ) 6, 1.8, 3.24
e ) 8, 1.9, 3.25
Solución .
El rango se define como:
x máx − x mín = 24 − 16 = 8
Para obtener la desviación estándar y varianza se obtiene la media aritmética
x=
Suma de los datos 384
=
= 19.2
Número de datos
20
y se aplican las fórmulas respectivas
x −x
20 - 19.2
17 - 19.2
20 - 19.2
21 - 19.2
16 - 19.2
18 - 19.2
19 - 19.2
17 - 19.2
18 - 19.2
20 - 19.2
19 - 19.2
21 - 19.2
18 - 19.2
17 - 19.2
19 - 19.2
21 - 19.2
22 - 19.2
18 - 19.2
24 - 19.2
19 - 19.2
0.8
- 2.2
0.8
1.8
- 3.2
- 1.2
- 0.2
- 2.2
- 1.2
0.8
- 0.2
1.8
- 1.2
- 2.2
- 0.2
1.8
2.8
- 1.2
4.8
- 0.2
(x − x)2
0.64
4.84
0.64
3.24
10.24
1.44
0.04
4.84
1.44
0.64
0.04
3.24
1.44
4.84
0.04
3.24
7.84
1.44
23.04
0.04
P
(x − x)2 = 73.2
P
(x − x)2 73.2
=
= 3.66
n
20
sP
(x − x)2 p
= 3.66 = 1.91
n
Varianza
Desviación estándar
Por tanto, la opción correcta es el inciso a.
1.6.4
Medidas de posición
Las medidas de posición son cantidades que dividen una colección ordenada de datos, en 4, 10
o 100 partes iguales.
Cuartiles
Los cuartiles son 3 números que dividen a la colección ordenada de datos en 4 partes iguales.
Sus valores pueden ser datos, o bien cantidades obtenidas al promediar dos datos consecutivos
de la colección ordenada. Cuartil 1 (Q 1 ): es un número tal que el 25 % de los datos son menores
o iguales a él y el 75 % de los datos son mayores o iguales a él. Su posición en la colección
ordenada se obtiene dividiendo el total de datos (n) entre 4.
Cuartil 2 (Q 2 ): coincide con la mediana porque es una cantidad tal que el 50 % de los datos son
menores o iguales a ella y el otro 50 % son mayores o iguales.
Cuartil 3 (Q 3 ): es un número tal que el 75 % de los datos son menores o iguales a él y el 25 % son
mayores o iguales. Su posición en la colección ordenada se obtiene multiplicando el total de
datos (n) por 34.
1.75
Cuartiles
Se tomó el tiempo (en minutos) que tardaron 16 niños en resolver un test psicológico.
Estos son los datos:
28, 20, 21, 20, 23, 25, 26, 19, 29, 22, 18, 30, 26, 29, 24, 25
Encontrar los cuartiles Q 1 ,Q 2 ,Q 3 .
a) Q 1 = 18, Q 2 = 25 y Q 3 = 30.
b) Q 1 = 20, Q 2 = 25 y Q 3 = 27.
c) Q 1 = 20.5, Q 2 = 24.5 y Q 3 = 27.
d) Q 1 = 28, Q 2 = 29 y Q 3 = 25.
e) Q 1 = 21, Q 2 = 25 y Q 3 = 29.
Solución .
Datos ordenados:
18, 19, 20, 20, 21, 22, 23, 24, 25, 25, 26, 26, 28, 29, 29, 30
Cuartil
Q1
Q2
Q3
Posición
1
4 (16) = 4, promedio 4° y 5°
2
4 (16) = 8, promedio 8° y 9°
3
4 (16) = 12, promedio 12° y 13°
Valor
20.5
24.5
27
Así que los cuartiles son: Q 1 = 20.5, Q 2 = 24.5 y Q 3 = 27.
Por tanto, la opción correcta es el inciso c.
1.76
Cuartiles
Las notas obtenidas por 21 estudiantes en un examen de matemáticas, son:
8.5, 10, 7, 7.5, 6, 5, 6.5, 8.5, 9, 7.5, 8, 10, 9.5, 9, 4, 5.5, 6, 7.5, 7, 7.5, 8
Encontrar los cuartiles Q 1 ,Q 2 ,Q 3 .
a) Q 1 = 5.5, Q 2 = 7.5 y Q 3 = 9.5.
b) Q 1 = 7.5, Q 2 = 8.5 y Q 3 = 9.5.
c) Q 1 = 7, Q 2 = 8 y Q 3 = 9.
d) Q 1 = 6, Q 2 = 7 y Q 3 = 8.
e) Q 1 = 6.5, Q 2 = 7.5 y Q 3 = 8.5.
Solución .
Datos ordenados:
4, 5, 5.5, 6, 6, 6.5, 7, 7, 7.5, 7.5, 7.5, 7.5, 8, 8, 8.5, 8.5, 9, 9, 9.5, 10, 10
Cuartil
Q1
Q2
Q3
Posición
1
4 (21) = 5.25, 6° lugar
2
4 (21) = 10.5, 11° lugar
3
4 (21) = 15.75, 16° lugar
Valor
6.5
7.5
8.5
Así que los cuartiles son: Q 1 = 6.5, Q 2 = 7.5 y Q 3 = 8.5.
Por tanto, la opción correcta es el inciso e.
Deciles
Se trata de 9 números que dividen a la colección ordenada de datos en 10 partes iguales. Se
denotan por D 1 , D 2 , D 3 , . . . , D 9 . Estas medidas se usan cuando la cantidad de datos es grande.
Sus valores se calculan de manera similar a la forma en que se calcularon los cuartiles.
El 10 % de los datos son menores o iguales que D 1 y el 90 % mayores o iguales.
El 20 % de los datos son menores o iguales que D 2 y el 80 % mayores o iguales.
El 30 % de los datos son menores o iguales que D 3 y el 70 % mayores o iguales. Y así sucesivamente.
Percentiles
Son 99 números que dividen a la colección ordenada de datos en 100 partes iguales. Se denotan
por P 1 , P 2 , P 3 , . . . , P 99 . Estos permiten determinar rangos de variación de cualquier porcentaje
de los datos. Por ejemplo, el 22 % de los datos son menores o iguales a P 22 y el 78 % son mayores
o iguales. El 65 % de los datos son menores o iguales que P 65 y el 35 % es mayor o igual.
1.6.5
Nociones de probabilidad
Existen dos tipos de eventos
Determinísticos.
Estocásticos o probabilísticos.
Si se arroja una moneda al aire es evidente que, por efecto de la gravedad, la moneda cae. Dicho
evento es invariable, por eso es un evento determinístico.
Al arrojar la moneda al aire, se da por hecho que caerá, lo que se desconoce es si la cara de la
moneda será sol o águila, por tanto, se trata de un evento estocástico o probabilístico.
El número total de eventos es también conocido como espacio muestral. En esta lección se
estudiaran únicamente los eventos probabilísticos. La probabilidad se define:
Número de casos favorables
Número total de casos
donde x es el evento estocástico o probabilístico.
P (x) =
1.77
Probabilidad
Al lanzar una moneda, ¿cuál es la probabilidad de obtener águila?
a) 100 %
Solución .
b) 75 %
c) 50 %
d ) 25 %
e ) 65 %
Evento probabilístico (x = lanzar la moneda).
P (x) =
Número de casos favorables
Número total de casos
Número de casos favorables = 1
Número total de casos = 2
(sólo una cara de la moneda es águila)
(número de caras en una moneda)
1
P (x) =
2
La probabilidad se expresa en fracción común 12 , fracción decimal 0.5, o como porcentaje
50 %.
Por tanto, la opción correcta es el inciso c.
1.78
Probabilidad
Al lanzar un dado, ¿qué probabilidad existe de obtener un número menor o igual que 4?
a) 0.25
b) 0.333...
c) 0.444...
d ) 0.666...
e ) 0.5
Solución .
Evento probabilístico (x = lanzar el dado).
P (x) =
Número de casos favorables
Número total de casos
Número de casos favorables = 4
Número total de casos = 6
(caras posibles, 1, 2, 3 y 4)
(número de caras en un dado)
4 2
P (x) = = = 0.666...
6 3
Por tanto, la opción correcta es el inciso d.
1.79
Probabilidad
En una urna hay 6 esferas rojas, 2 azules y 2 verdes. ¿Cuántas esferas hay que sacar, para
tener la certeza de tener 2 esferas azules?
a) 10
b) 8
c) 4
d)2
e)6
Solución .
Sacar una esfera de la urna es un evento estocástico, por tanto, la primera esfera puede
ser roja, verde o azul. Entonces para tener la certeza de que se tengan 2 esferas azules,
se deben de extraer la suma del número de esferas de los demás colores y el número de
esferas del color que se desea.
6 esferas rojas + 2 esferas verdes + 2 esferas azules = 10 esferas.
Por tanto, la opción correcta es el inciso a.
1.80
Probabilidad
En un grupo de 20 personas, 3 cuartas partes saben nadar, de las cuales una tercera parte
son mujeres. ¿Cuál es la probabilidad de que al escoger a un representante del grupo,
dicha persona sea una mujer que sepa nadar?
a) 0.10
b) 0.25
c) 0.5
d ) 0.75
e ) 0.333...
Solución .
Las tres cuartas partes del grupo son las personas que saben nadar.
µ ¶
3
(20) = 15 personas que saben nadar.
4
µ ¶
1
(15) = 5 mujeres que saben nadar.
3
Evento probabilístico (x = escoger una persona).
P (x) =
Número de casos favorables
Número total de casos
Número de casos favorables = 5
Número total de casos = 20
(personas que son mujeres y saben nadar)
(número total de personas del grupo)
5
1
P (x) =
= = 0.25
20 4
Por tanto, la opción correcta es el inciso b.
1.81
Probabilidad
En una bolsa hay 15 golosinas de vainilla, 10 de café y 5 de chocolate. ¿Qué probabilidad
existe de sacar una golosina que NO sea de chocolate?
a) 83.3 %
b) 66.6 %
c) 50 %
d ) 16.6 %
e ) 75 %
Solución .
Evento probabilístico (x = sacar una golosina).
Número de casos favorables = 25
Número total de casos = 30
(número de golosinas que NO son de chocolate)
(número total de golosinas)
25 5
P (x) =
= = 0.833 = 83.3 %
30 6
Por tanto, la opción correcta es el inciso a.
2
Pensamiento Analítico
Integración de la información
En el nivel superior son de suma importancia las capacidades de análisis y síntesis. Ambas nos
hablan de la habilidad de verificar datos y conceptualizarlos, lo que es necesario, primero, para
la correcta asimilación del conocimiento y, en segundo lugar, para reafirmarlo y producirlo,
posteriormente. De aquí que sea menester la verificación de esta capacidad en el estudiante
que pretende ingresar al nivel superior. Para ello, existen diversas maneras de constatación, las
cuales se desglosarán en lo que viene.
Información textual
La primera manera de corroborar la posesión de habilidades tan necesarias es la lectura. El
estudiante debe ser capaz de visualizar causas, consecuencias, contextos, inferencias y demás,
a partir de datos proporcionados, que van desde un gráfico hasta un escrito. La lectura debe
realizarse de manera global, seguir las premisas para poder captar la generalidad de las ideas
e identificar las ideas centrales, de las cuales se derivan inferencia de causas, consecuencia,
significación de contextos específicos, relaciones diversas, entre otras.
Lee y después contesta las preguntas sobre el texto de Descartes.
Sobre la metafísica, en las que se demuestra la existencia de Dios y la distinción del alma y del
cuerpo (Primera meditación) Y me percaté hace algunos años de cuántas opiniones falsas admití
como verdaderas en la primera edad de mi vida y de cuán dudosas eran las que después construí sobre aquéllas, de modo que era preciso destruirlas de raíz para comenzar de nuevo desde
los cimientos si quería establecer alguna vez un sistema firme y permanente; con todo, parecía
ser esto un trabajo inmenso, y esperaba yo una edad que fuese tan madura que no hubiese de
sucederle ninguna más adecuada para emprender esa tarea. Por ello, he dudado tanto tiempo,
que sería ciertamente culpable si consumo en deliberaciones el tiempo que me resta para intentarlo. Por tanto, habiéndome desembarazado oportunamente de toda clase de preocupaciones,
me he procurado un reposo tranquilo en apartada soledad, con el fin de dedicarme en libertad a
la destrucción sistemática de mis opiniones.
Para ello no será necesario que pruebe la falsedad de todas, lo que quizá nunca podría alcanzar;
sino que, puesto que la razón me persuade a evitar dar fe no menos cuidadosamente a las cosas
que no son absolutamente seguras e indudables que a las abiertamente falsas, me bastará para
rechazarlas todas encontrar en cada una algún motivo de duda. Así pues, no me será preciso examinarlas una por una, lo que constituiría un trabajo infinito, sino que atacaré inmediatamente
los principios mismos en los que se apoyaba todo lo que creí en un tiempo, ya que, excavados los
cimientos, se derrumba al momento lo que está por encima edificado.
Pensamiento Analítico
2.1
60
Todo lo que hasta ahora he admitido como absolutamente cierto lo he percibido de los sentidos o
por los sentidos; he descubierto, sin embargo, que éstos engañan de vez en cuando y es prudente
no confiar nunca en aquéllos que nos han engañado aunque sólo haya sido por una sola vez.
Con todo, aunque a veces los sentidos nos engañan en lo pequeño y en lo lejano, quizás hay
otras cosas de las que no se pueden dudar aun cuando las recibamos por medio de los mismos,
como, por ejemplo, que estoy aquí, que estoy sentado junto al fuego, que estoy vestido con un
traje de invierno, que tengo este papel en las manos y cosas por el estilo. ¿Con qué razón se puede
negar que estas manos y este cuerpo sean míos? A no ser que me asemeje a no sé qué locos cuyos
cerebros ofusca un pertinaz vapor de tal manera atribulario que aseveren en todo momento que
son reyes, siendo en realidad pobres, o que están vestidos de púrpura, estando desnudos, o que
tiene un jarra en vez de cabeza, o que son unas calabazas, o que creados de vidrio; pero ésos son
dementes, y yo mismo parecería igualmente más loco que ellos si me aplicase esos ejemplos.
Perfectamente, como si yo no fuera un hombre que suele dormir por la noche e imaginar en
sueños las mismas cosas y a veces, incluso, menos verosímiles que esos desgraciados cuando están despiertos. ¡Cuán frecuentemente me hace creer el reposo nocturno lo más trivial, como, por
ejemplo, que estoy aquí, que llevo puesto un traje, que estoy sentado junto al fuego, cuando en
realidad estoy echado en mi cama después de desnudarme! Pero ahora veo ese papel con los ojos
abiertos, y no está adormilada esta cabeza que muevo, y consciente y sensiblemente extiendo mi
mano, puesto que un hombre dormido no lo experimentaría con tanta claridad; como si no me
acordase de que he sido ya otras veces engañado en sueños por los mismos pensamientos. Cuando doy más vueltas a la cuestión, veo sin duda alguna que estar despierto no se distingue con
indicio seguro del estar dormido y me asombro de manera que el mismo estupor me confirma en
la idea de que duermo.
Pues bien: soñemos, y que no sean, por tanto, verdaderos esos actos particulares; como, por ejemplo, que abrimos los ojos, que movemos la cabeza, que extendemos las manos; pensamos que
quizá ni tenemos tales manos ni tal cuerpo. Sin embargo, se ha de confesar que has sido vistas
durante el sueño como unas ciertas imágenes, pintadas que no pudieron ser ideadas sino a la
semejanza de cosas verdaderas y que, por lo tanto, estos órganos generales (los ojos, las cabeza,
las manos y todo el cuerpo) existen, no como cosas imaginarias, sino verdaderas; puesto que los
propios pintores ni aún siquiera cuando intentan pintar las sirenas y los sátiros con las formas
más extravagantes posibles, pueden crear una naturaleza nueva en todos los conceptos, sino que
entremezclan los miembros de animales diversos; incluso si piensan algo nuevo de tal manera
que nada en absoluto haya sido visto que se les parezca ciertamente, al menos deberán ser verdaderos los colores con los que se componga ese cuadro. De la misma manera, aunque estos órganos
generales (los ojos, la cabeza, las manos, etc.), puedan ser imaginarios, se habrá de reconocer al
menos otros verdaderos más simples y universales, de los cuales como de colores verdaderos son
creadas esas imágenes de las cosas que existen en nuestro conocimiento, ya sean falsas, ya sean
verdaderas.
En consecuencia, deduciremos quizá sin errar de lo anterior que la física, la astronomía, la medicina y todas las demás disciplinas que dependen de la consideración de cosas compuestas, son
ciertamente dudosas, mientras que la aritmética, la geometría y otras de este tipo, que tratan sobre las cosas más simples y absolutamente generales, sin preocuparse de si existen en realidad en
la naturaleza o no, poseen algo cierto e indudable, puesto que, ya esté dormido, ya esté despierto, dos y tres serán siempre cinco y el cuadrado no tendrá más que cuatro lados; y no parece ser
posible que unas verdades tan obvias incurran en sospecha de falsedad.
Contestar los siguientes ejemplos a partir de la información dada:
2.1
Texto de Descartes
¿Cuál es la idea principal del texto?
a) rechazar todos los datos que no pueda comprobar
b) afirmar que la física, la astronomía y la medicina, son dudosas
c) establecer un sistema de conocimientos firme y permanente
Solución .
La respuesta es c, ya que el primer párrafo muestra el objetivo del texto y cómo se había
llegado a esto: de modo que era preciso destruirlas de raíz para comenzar de nuevo desde
los cimientos si quería establecer alguna vez un sistema firme y permanente, lo cual se
ve reforzado cuando al final del párrafo agrega: Por tanto, habiéndome desembarazado
oportunamente de toda clase de preocupaciones, me he procurado un reposo tranquilo
en apartada soledad, con el fin de dedicarme en libertad a la destrucción sistemática de
mis opiniones.
2.2
Texto de Descartes
¿Cómo haría el escritor para destruir los datos falsos que concebía como verdaderos?
a) atacarlos de uno por uno
b) destruir los cimientos
c) desechar sus opiniones
Solución .
La respuesta es b. Ello porque indica en el párrafo 2: Así pues, no me será preciso examinarlas una por una, lo que constituiría un trabajo infinito, sino que atacaré inmediatamente los principios mismos en los que se apoyaba todo lo que creí en un tiempo, ya que,
excavados los cimientos, se derrumba al momento lo que está por encima edificado.
2.3
Texto de Descartes
¿Cuál es la valoración que tiene el filósofo de ciencias como la física, astronomía y medicina?
a) que no eran dignas de consideración por tratar de datos cambiantes, sujeto en su
valoración a los sentidos
b) que eran ciencias y por tanto dignas de prestigio
c) que su objeto de estudio era verificable
Solución .
La respuesta es a) porque en el último párrafo expresó: la física, la astronomía, la medicina y todas las demás disciplinas que dependen de la consideración de cosas compuestas,
son ciertamente dudosas, mientras que la aritmética, la geometría y otras de este tipo,
que tratan sobre las cosas más simples y absolutamente generales, sin preocuparse de si
existen en realidad en la naturaleza o no, poseen algo cierto e indudable.
En lo que a la lectura se refiere, existen múltiples perspectivas de evaluación. Por ejemplo, la
anterior gira en torno a la comprensión de contenido. De la misma forma, los ejercicios de este
tipo pueden girar en torno a aspectos de estructura y estilo de la redacción, como por ejemplo,
el tipo de texto, la función comunicativa que cumple, identificar el emisor, si tiene la estructura
completa, etc.
Demonios de Tasmania, una carrera contra el cáncer y la extinción
Héctor Rodríguez
Del tamaño de un perro pequeño, musculoso y robusto, Sarcophilus harrisii es el marsupial carnívoro más grande que queda en el mundo tras la extinción del último e icónico tilacino, o lobo
marsupial. Su mal olor, el desagradable sonido que emite cuando se siente amenazado, y una fiereza sin parangón a la hora de alimentarse le han valido a esta bestia en miniatura su merecido
apodo de diablo o demonio.
Y es que quizá resulte que el tiempo nos acabe dando la razón y un día descubramos que este
pequeño marsupial es un auténtico diablo en el sentido más literal de la palabra, pues la muerte parece perseguirle, pero el demonio de Tasmania no está dispuesto a dejarse atrapar. Donde
otros marsupiales, más grandes, más fuertes, más fieros y mejor armados han sucumbido, este pequeño diablo siempre ha cabalgado triunfante esquivando la desaparición hasta nuestros
días.
Considerados una amenaza para el ganado y perseguidos hasta la extenuación, el diablo de Tasmania anduvo a principios de siglo al borde de ser relegado al registro fósil hasta que su inclusión
en 1941 en la lista de especies amenazadas propició la recuperación de sus poblaciones. No obstante, 10 lustros después, durante la década de los años 90, la especie se vio amenazada por un
cáncer facial contagioso que redujo de nuevo sus poblaciones drásticamente hasta volver a ser
declarada en peligro de extinción en el año 2008.
El primer caso documentado de este cáncer se registró en Australia en el año 1995, y aunque
pueda resulta extraño, la llamada enfermedad tumoral facial del diablo de Tasmania -DFTD
por sus siglas en inglés- es contagiosa. Esta se extiende por transmisión directa de las células
cancerígenas vivas a través de las mordeduras y heridas que se infligen los animales en la cara
durante los percances y desavenencias que exhiben a la hora de alimentarse y aparearse. Se trata
de una forma mortal, muy agresiva y transmisible de cáncer facial que se encuentra en el 95 %
del rango geográfico del animal y la cual se estima que es responsable de la disminución del 80 %
de todas las poblaciones de la especie.
2.4
Texto de Demonios de tasmania
¿Qué tipo de texto es?
a) literario
b) personal
c) expositivo
Solución .
Respuesta b). Este tipo de textos es resultado de una investigación, la cual se difunde
entre la población para dar a conocer los nuevos descubrimientos.
2.5
Texto de Demonios de Tasmania
La parte de la estructura que falta en este escrito es
a) introducción
b) desarrollo
c) conclusión
Solución .
Respuesta: c). El texto carece de cierre, deja la temática suelta.
2.6
Texto de Demonios de Tasmania
la función comunicativa que cumple es
a) apelativa
b) poética
c) referencial
Solución .
Respuesta c). Esta función se encarga de describir hechos, cual es el caso de una investigación científica
2.7
Texto de Demonios de Tasmania
DFTD corresponde a un
a) neologismo
b) tecnicismo
c) latinismo
Solución .
Respuesta b), puesto que es un término desarrollado explícitamente para referirse a un
evento especializado de un área.
2.8
Texto de Demonios de Tasmania
El dato faltante en la introducción es
a) el objetivo
b) la referencia al cáncer
c) el tema
Solución .
Respuesta b). La introducción debe contener el tema a tratar, completo, el cual está contemplado en el título, pero no aparece mencionado en la introducción.
2.2
Interpretación de relaciones lógicas
La lógica fue desarrollada por Aristóteles en el siglo IV a. C. Su intención al hacerlo fue desarrollar un método eficiente para comprobar la verdad y poder clasificar los eventos de manera
real, apegándose a los hechos, en un contexto en el que aún se pretendían explicar los fenómenos naturales, atribuyéndolos a la voluntad de los dioses. Entre los diferentes mecanismos
desarrollados para probar la verdad se encuentra la analogía.
Este es un procedimiento mediante el cual se establece una relación de semejanza o diferencia
entre varios elementos. Para verificar el adecuado manejo de este tipo de razonamientos, las
estructuras más comunes son:
*como oraciones: se organiza con dos oraciones cortas, cuyo nexo es regularmente el enlace
como. Ve el ejemplo:
Vino es a uva como sidra es a manzana
Para saber si la relación es adecuada, debemos ubicar la conexión existente entre los dos elementos de la primera oración. Se tiene que verificar a qué clasificación de entes pertenecen los
términos y cómo se conectan, lo cual debemos comprender en términos tan sencillos, fuera
del vocabulario dado, que sea posible identificar si la relación dada en la segunda oración es
correcta, o en el examen, saber elegir el término que haga falta o la oración más adecuada que
preserve la misma relación. En el ejemplo dado, los dos términos de la primera oración son
vino y uva. Su relación, la cual puede expresarse de múltiples maneras, sería, por ejemplo, la
clasificación del vino como bebida embriagante y la uva como su materia prima. Si verificamos
los términos de la segunda oración, veremos que esta relación se cubre, pues la sidra también
es una bebida alcohólica, mientras que la manzana corresponde al material del que se elabora.
Identificado esto, podemos establecer otras analogías correctas, como: sake es a arroz, cebada
a cerveza, agave a tequila o charanda a caña.
¡Atención! En realidad no importa el orden en que aparezcan los términos, sino que se cumpla
la relación en ambas oraciones:
vino es a uva como manzana a sidra ⇄ uva es a vino como sidra a manzana,
aunque lo regular es que aparezcan en el mismo orden.
Este tipo de mecanismos puede prestarse para evaluar cualquier contenido, desde la gramática
de un lenguaje, hasta datos científicos.
2.9
Relaciones Lógicas
Agua es oxígeno como plátano a
a) cáscara
b) potasio
c) fruta
Solución .
La respuesta es b), dado que la relación existente entre los términos de la primera oración
es un elemento y un compuesto que contenga al primero.
2.10
Relaciones Lógicas
ácido acetilsalicílico es a cefalea como ampicilina a
a) disentería
b) dolor de cabeza
c) infección
Solución .
La respuesta es c), dado que la ampicilina es un derivado de la penicilina, que ayuda a
disminuir las infecciones. Esto porque la relación es medicamento y afección que ayuda
a controlar.
2.11
Relaciones Lógicas
Hereje es a cristiano como pagano a
a) otra religión
b) no creyente
c) demoníaco
Solución .
La respuesta es a). Solo alguien que ha sido educado bajo los preceptos del cristianismo
puede ser denominado hereje, ya que el hereje no es un ateo, sino una persona que cree,
pero que se manifiesta en contra de la versión oficial del credo, como que una mujer
soltera se embarace, o si cometes suicidio te vas al infierno, o que los homosexuales no
son bienvenidos en el seno de Dios, etc. Pagano o gentil solo es aquella persona que no
practica el cristianismo, dado que sus deidades y las de su comunidad son distintas.
Otra manera de evaluarlo es con frases sinónimas pero cuya escritura tenga diferentes palabras
o sentido contrario al que sirva de referencia. Por ejemplo: no saber es lo mismo que ignorar; la
primera contiene una negación, mientras que la segunda es solo una palabra sola, lo cual equivale a que es positiva. Haciendo una analogía: así como en matemáticas no se pone el signo a
los números positivos, así tampoco se pone signos a las palabras, pero cuando aparecen vocablos como no, ningún, nada, nadie, no todos, nunca, etc., estas palabras u oraciones deberán
contemplarse como negativas.
2.12
Relaciones Lógicas
Identifica la frase que tenga el mismo sentido que Al titubear:
a) al no mostrar inseguridad
b) al no estar seguro
c) al aseverar
Solución .
Respuesta b). Aseverar, afirmar algo, y no inseguridad (=seguridad), enfocan el dominio o
conocimiento sobre una situación, mientras que titubear, dudar, implica la incertidumbre sobre una situación o evento.
2.13
Relaciones Lógicas
Elige la frase que tenga el mismo sentido que: Grosso modo
a) sin particularidades
b) en términos concretos
c) etcétera
Solución .
Respuesta a). Grosso modo, literalmentemodo grueso, sinónimo de en términos generales, implica una panorámica de un asunto o evento, contrario a en términos concretos.
Etcétera, no tiene ninguna relación con los otros dos vocablos.
2.14
Relaciones Lógicas
Elige la frase sinónima de al no depender
a) ser heterónomo
b) al cumplir los propios deseos
c) ser autónomo
Solución .
Respuesta c). La autonomía es la capacidad con que cuenta una persona para tomar sus
propias decisiones y elegir a conciencia. Muy por el contrario, la heteronomía conlleva
el hecho de que alguien más hace reglas y nos las impone, coartando la elección de la
persona implicada. El cumplir los propios deseos no se relaciona con este ámbito de
decisión personal.
A la par, existen en la lógica otras estructuras de razonamiento, como los silogismos. Silogismo
significarazonamiento encadenado o cadena de pensamientos. Los hay de estructura sencilla,
como el condicional, disyuntivo o entimema, o ya más estructurados, como el categórico.
Si A, entonces B
A, Luego B
Si A, entonces B
lo tanto, No A
seriedad
es decir;
es decir;
es decir;
es decir;
Si estudias con seriedad, entonces pasarás el examen
estudiaste con seriedad, luego pasaste el examen
Si estudias con seriedad, pasarás el examen No B por
No pasaste el examen por lo tanto, no estudiaste con
Silogismo disyuntivo: la premisa mayor es disyuntiva. No da lugar más que a dos opciones.
es decir;
es decir;
O es A o es B
Es A Luego, no B
o estudias o trabajas
estudias, luego no trabajas
Entimema: Se manifiesta es una sola oración. Tiene la forma de los dichos y refranes. Tiene un
solo dato del que se pasa a la conclusión.
No estudiaste, luego no sabes nada.
2.15
Silogismos
Elige la opción que completa el razonamiento: Como no estudiaste
a) pasaste el examen
b) sacaste 10
c) usaste un acordeón
Solución .
Respuesta c), pues las otras indican algo positivo que no se sigue con consecuencia del
hecho descrito.
2.16
Silogismos
Si uso influencias para realizar un trámite oficial, cometo un acto de corrupción. El papá
de un amigo me ayudó a entrar a la escuela que quería, luego
a) mi amigo me aprecia de verdad
b) cometí un acto de corrupción
c) puedes entrar a la escuela que quieras si conoces a alguien que trabaje ahí
Solución .
Respuesta b), ya que se cometió tráfico de influencias y eso, es corrupción.
En lo que respecta al silogismo categórico, este tiene una estructura bien definida que hace que
se pueda entender fácilmente. Posee tres oraciones completas, cada una con su propio sujeto,
verbo y predicado; en total, solo aparecerán 3 términos, esto es, palabras que nos indican el
sujeto y el predicado. Las dos primeras oraciones se llaman premisas y son los antecedentes,
mientras que la última es la conclusión o el resultado. Analicemos el ejemplo clásico:
(primera premisa)
(segunda premisa)
(Conclusión )
Todos los hombres son mortales
Sócrates es hombre
Sócrates es mortal
Solo pueden aparecer 3 términos, en este caso, hombre, mortal y Sócrates. Puede haber cambios
en género y número, los cuales no son relevantes mientras aparezcan las mismas palabras. Otro
elemento a considerar es el signo: se considera negativa una oración si contiene palabras como
no, nada, nadie, no todo, no es, o sinónimos; caso contrario, la oración se considerará positiva
y se aplica la ley de los signos. Si le quitamos una oración, habría que identificar la faltante a
partir de los datos que tenemos:
(primera premisa)
(segunda premisa)
(conclusión)
Ningún mortal es inmortal
Los santos fueron mortales
Primero identifico los 3 términos, que son mortal, inmortal y santos. El que ya aparece 2 veces,
no puede volver a hacerlo, en este caso mortal/mortales. Después, verifico el signo: ningún es
negativo, por lo cual la primera premisa lo es de igual manera; la segunda oración carece de
partícula negativa, por lo tanto, es positiva, lo que da negativo o menos, por positivo o más,
equivale a que la oración faltante sea negativa y contenga las palabras que están una sola vez.
En este caso, la conclusión es:
Ningún santo es inmortal
2.17
Premisas
Elige la respuesta correcta: Todos las las semillas son frutos-Todas los frutos son vegetales
a) ningún vegetal es semilla
b) Todas las semillas son vegetales
c) algunas semillas son frutos
Solución .
La respuesta es b). Tenemos 3 términos; cada uno se repite dos veces, se cumple con el
signo y es verdadera. No olvides que vegetal es el reino, que no es sinónimo de verdura.
2.18
Premisas
Elige la respuesta correcta: Todas las personas tienen el potencial de aprender-un niño
con síndrome de Down tiene potencial de aprender
a) un niño con síndrome de Down es una persona
b) John Langdom Down es una institución para personas Down
c) algunos niños no tienen potencial de aprender
Solución .
Respuesta: a). Se cumple con los tres términos, el signo y es verdadera.
2.3
Estructura de la lengua
La gramática es el estudio del lenguaje. Abarca desde la historia, significado y evolución de
las palabras con las etimologías, hasta la pronunciación con la fonética, las variaciones del
significado con la semántica, las 9 partículas que integran las oraciones con la analogía, hasta
la escritura correcta con la ortografía. Para esta ocasión, nos quedaremos solamente con la
analogía, que estudia las 9 partes que constituyen la oración y las analiza por separado con sus
diferentes accidentes (género, número y persona, si es verbo)
Verbos
Los verbos son las partículas que nos indican acción dentro de la oración. Estos tiene varios
accidentes o cambios, como son número (singular y plural), persona (quien realiza la acción:
yo, tú, él/ella, nosotros, ustedes y ellos), tiempo (10 de indicativo y 6 de subjuntivo) y modo (la
manera en que se realiza la acción: en la realidad, en la posibilidad y las órdenes).
Perífrasis: verbo conjugado y verbo no personal
Primero, cuando un verbo termina en -ar, -er, -ir se encuentra en abstracto, lo que quiere decir
que se encuentra sin conjugar, sin variaciones. Por el contrario, cuando se ha variado e integra
información de quién y cuándo se realizó la acción, se dice que está conjugado. Por ejemplo,
si usamos definen, la acción se encuentra en presente y se refiere a ellos o ustedes, o dicho en
términos gramaticales, corresponde al presente, 2a. o 3a. persona del plural.
2.19
Verbos
Identifica el verbo sin conjugar:
a) manjar
b) enfatizar
c) maxilar
Solución .
Respuesta: b). a) y c) son sustantivos, a) sinónimo de comida deliciosa y c) una de las dos
partes de la boca
2.20
Verbos
Identifica el verbo en pasado o pretérito:
a) vendrá
b) vino
c) venía
Solución .
Respuesta: b). a) se encuentra en futuro; c), en copretérito.
Tiempos verbales simples y compuestos
Cuando un verbo indica tiempo y persona, está conjugado. Existen, por otra parte, tiempos
simples, un solo verbo conjugado en algún tiempo (viniste), y tiempos compuestos, dos verbos, uno de ellos el verbo haber, conjugado en el tiempo en cuestión, seguido de un verbo en
participio (había estado).
Observación
Cuando se agrega el gerundio (terminación -ando, -endo) no se cambia el tiempo, se
construye la idea de duración, pero el tiempo sigue siendo el mismo (estoy pensando).
2.21
Tiempos Verbales
a) vendrá
b) vino
c) venía
Solución .
Respuesta: b). a) se encuentra en futuro; c), en copretérito.
2.22
Tiempos Verbales
a) estaba
b) estado
c) esperando
Solución .
La respuesta es a), que se encuentra en copretérito. b) necesita del verbo haber conjugado para adquirir sentido, mientras que c) requiere de un verbo conjugado para dar la
idea de acción que se prolonga por cierto periodo de tiempo.
2.23
Tiempos Verbales
Elige la opción que contiene un tiempo simple progresivo o continuo:
a) estaba pensando
b) estado pensando
c) estando pensando
Solución .
La respuesta es a). b) necesita del verbo haber conjugado y c) no se usa en español.
El español maneja 3 modos, que son las formas en que se realiza la acción. El subjuntivo o
modo de la no realidad refleja deseos, puntos de vista, aspiraciones u opiniones. Por ejemplo,
en indicativo o modo de la realidad, se dice: voy a la escuela por las mañanas, como hecho,
mientras que, en modo subjuntivo, se expresaría: cuando vaya a la escuela te buscaré, lo cual
no es garantía de que vaya a ocurrir, no es un hecho.
2.24
Verbos subjuntivos
Identifica el ejemplo que incluya un verbo que no se encuentre en subjuntivo:
a) yo no pude venir ayer
b) si fuera posible, compraría un auto
c) hubieras llegado temprano y hubieras encontrado un regalo
Solución .
Respuesta: a), pues remite a un hecho, mientras que los otros corresponden a situaciones
que no son reales.
El tiempo presente de subjuntivo sufre un ligero cambio respecto al presente de indicativo:
Indicativo
Vengo
puedes
está
2.25
Cambia
-o por -a en primera persona
-es por -as en segunda persona
-a por -e en tercera persona
Subjuntivo
venga
puedas
esté
Tiempos Verbales
Elige la opción que contenga un verbo que no esté en subjuntivo
a) quiera
b) tengas
c) bailaré
Solución .
Respuesta: c), puesto que está en futuro de indicativo o de la realidad.
Sustantivos
Los sustantivos son nombres de personas, animales o cosas. Estas palabras pueden tomar diferentes funciones en la oración.
2.26
Sustantivos
Identifica cuántos sustantivos hay en el fragmento: En 1995 fue identificado el primer
caso de cáncer contagioso en Australia, en la Isla de Tasmania
a) 5
b) 6
c) 2
Solución .
Respuesta: a), caso, cáncer, Australia, isla y Tasmania.
2.27
Tiempos Verbales
Identifica cuántos sustantivos hay en el fragmento: Los varones también tienen la posibilidad de gestar y amamantar a sus hijos, según ha revelado la ciencia
a) 7
b) 3
c) 4
Solución .
Respuesta: c), varones, posibilidad, hijos y ciencia.
Por su parte, los adjetivos son características que matizan al sustantivo. Por ejemplo, si tenemos
el sustantivo o nombre niño, las diversas variaciones que puede tener, serán adjetivos: pequeño, pelirrojo, mexicano, latoso y dormilón. Existen diferentes clasificaciones de estos, que van
desde los tamaños, figuras, formas o cosas físicas, pasando por los números en todas sus variaciones, las posesiones, distancias y hasta las características morales de una persona. La clave
es detectar que cerca de esta categoría de vocablos se encuentra el nombre de algo antes o
después (mi hijo, esa casa, niño latoso).
2.28
Adjetivos
Identifica cuántos adjetivos hay en el fragmento: En cuanto entró, lo vi: tenía un sombrero, rojo y grande, que le había costado el doble de dinero que el que tenía en la casa
vieja
a) 5
b) 4
c) 1
Solución .
Respuesta: b), rojo, grande, doble y vieja.
2.29
Adjetivos
Identifica cuántos adjetivos hay en el fragmento: El ornitorrinco es un verdadero mutante de la naturaleza: tiene pico y patas de pato, cuerpo y cola de castor, pone huevos,
amamanta a sus crías y los machos tienen un espolón venenoso en las patas traseras
a) 10
b) 7
c) 4
Solución .
Respuesta: c), verdadero, mutante, venenoso, traseras.
Por su parte, también tenemos a los adverbios. Así como el adjetivo matiza al sustantivo, de
la misma manera el adverbio matiza al verbo (llegué: temprano, tarde, hoy, mañana, siempre,
no?). Su lugar es cercano al verbo a acción.
2.30
Adverbios
Identifica los adverbio que se encuentran en el fragmento: ¡nunca llegas temprano! ¡Siempre tengo que levantarte para que llegues a la escuela!
a) 2
b) 0
c) 3
Solución .
Respuesta: c), nunca, temprano, siempre.
2.31
Adverbios
Identifica los adverbio que se encuentran en el fragmento: difícilmente podía sostenerse
en ambos pies: daba la apariencia de ser un muerto
a) 3
b) 1
c) 0
Solución .
Respuesta: b), difícilmente.
Las preposiciones son partículas que nos ayudan a pegar palabras (vengo __ casa; paso __ ti).
Existe una lista determinada que se enseña en nivel básico (a, ante, bajo, cabe, con, contra, de,
desde).
2.32
Preposiciones
Relaciona las columnas
Ejemplo
Significado
1.-Juan heredó los terreno de su
padre Ejemplo
2.-Juan heredó los terrenos con
su padre
3.-Juan heredó los terrenos a su
padre
a.-Juan recibió los terrenos junto con su padre,
después de que alguien murió
b.-Juan murió y le dejó los terrenos a su padre
a) 1a, 2b, 3c
b) 1c, 2a, 3b
c.-El padre de Juan murió y le dejó los terrenos a él
c) 1c, 2a, 3b
Solución .
Respuesta c), de señala origen o dirección, con señala compañía y a dirección o punto
de llegada.
La ortografía es la parte de la gramática que se encarga de la correcta escritura de las palabras.
Abarca tanto la escritura con las letras correspondientes, como la colocación de acentos en las
sílabas tónicas, de acuerdo a las reglas de acentuación. De igual manera, abarca el uso de los
signos de puntuación.
2.33
Tiempos Verbales
Relaciona las columnas
Signo de puntuación
1.- coma
2.- punto y coma
Puntos suspensivos
Dos puntos
Uso
a.-Dejan en suspenso una idea
b.-Anuncian una información que está por venir
c.-Omite la repetición de un sujeto, predicado o
verbos recién mencionados; agrega información
adicional y antecede a palabras que señalan dificultad
d.-Sirven para separar oraciones en un mismo párrafo o anteceden palabras que indican dificultad
a) 1-b, 2a, 3c, 4d
b) 1d, 2c, 3b, 4a
c) 1c, 2d, 3a, 4b
Solución .
Respuesta: c).
En lo tocante a la acentuación, recordemos que hay reglas que guían la colocación de la tilde.
2.34
Acentuación
Si la regla expresa: todas las palabras agudas terminadas en n, s o vocal llevan acento,
¿cuál de las siguientes palabras debería tener acento escrito?
a) fue
b) dio
c) vio
c) todas
c) ninguna
Solución .
La respuesta es e). En el caso de las palabras monosílabas, el acento es innecesario, a
menos que sea para evitar una confusión, como ocurre con el uso del acento diacrítico,
donde es usado para distinguir homónimos (te, té).
Las palabras sobreesdrújulas no existen de manera natural en el español. Son resultado de la
fusión de verbos con pronombres, pues de lo contrario, no se podría acentuar antes de la antepenúltima sílaba.
2.35
Acentuación
Identifica las palabras que son sobreesdrújulas: (1) dámelo, (2)póngaselo, (3)cártel,
(4)cárcel
a) 1 y 2
b) 2 y 4
c) 2
c) 3
Solución .
Respuesta c): ya que la palabra es la fusión de un verbo con dos pronombres.
2.36
Acentuación
Elija la opción correcta que explica por qué las palabras volumen y examen no llevan
acento en singular, pero sí en plural:
a) es falso, todas estas palabras llevan acento, estén en singular o en plural
b) no, es a la inversa, en singular llevan acento, pero en plural, no
c) en singular son graves y terminan en n, pero al hacerlas plurales, se agrega una sílaba
más y se transforman en esdrújulas
Solución .
La respuesta es c).
El acento diacrítico es aquel que ayuda a distinguir el significado de homónimos, es decir, palabras que se escriben exactamente igual, pero tienen significados distintos.
2.37
aAcento diacrítico
Elige el par de palabras que se aplican a este caso:
a) tu-tú
b) bota-vota
c) arroyo-arrolló
Solución .
Respuesta: a). Tú de persona, pronombre, y tu, posesivo, se escriben exactamente igual,
pero el acento nos facilita la distinción entre una acepción y otra.
En esta misma categoría entra el uso de las grafías o letras. La escritura depende, muchas veces,
del origen de las palabras, de la adaptación que una cultura haya hecho de ellas o simplemente
de un acuerdo que se haya tomado.
2.38
Grafías
Elige la frase que contenga la explicación al siguiente caso: Las palabras terminadas en z
hacen el plural cambiando la grafía por una c. En el caso del verbo nacer, se coloca z en
medio porque:
a) en pez y vez la z está al final y cuando el sonido queda en medio, la letra se modifica
b) nacer no lleva z, pero al conjugar, si no le agregamos la grafía, diría yo naco
c) la z es un comodín que se coloca sin ninguna regla
Solución .
Respuesta: b).
Otra rama de la gramática es la semántica. Esta estudia el significado de las palabras y la identificamos como manejo de vocabulario.
2.39
Semántica
¿Cuál opción contiene vocablos sinónimos?
a) indigente-diligente
b) negligente-irresponsable
c) frecuente-transeúnte
Solución .
Respuesta: b).
2.40
Semántica
¿Cuál opción contiene palabras contrarias?
a) migrar-emigrar
b) emigrar-inmigrar
c) migrar-inmigrar
Solución .
Respuesta: b), ya que son antónimos. Aunque las dos parten de una raíz común, migrar;
viajar, moverse, una indica hacia afuera (e-) y la otra hacia adentro (-in).
2.41
Semántica
¿Cuál homófono completa correctamente la oración?
a) has
b) haz
c) as
Solución .
Respuesta: b). Las otras opciones corresponden a hacer y experto.
3
3.1
3.1.1
79
Inglés como lengua extranjera
Comprensión lectora
Read the article in order to choose the correcte answer.
Madagascar - When to go
Madagascar has two seasons, a warm, wet season from November to April, and a cooler dry
season between May and October. However, different parts of the country have very different
weather. The east coast is hotter and wetter, with up to 4000mm of rainfall per year. In the rainy
season, there are strong winds, and these can cause a lot of damage. Avoid visiting eastern Madagascar between January and March because the weather can make road travel very difficult.
The dry season is cooler and more pleasant. The high, central part of the country is much drier
and cooler. About 1,400 mm of rain falls in the rainy season, with some thunderstorms, but
the summer is usually sunny and dry, but it can be cold, especially in the mornings, with freezing showers, and it may snow in mountain areas above 2,400m, and even stay there for several
days. The west coast is the driest part of the island. Here, the winter months are pleasant with
little rain, cooler temperatures and blue skies. The summers can be extremely hot, especially in
the southwest. This part of the country is semi-desert, and only gets around 300mm of rain per
year.
1.- Madagascar has 4 seasons: spring, summer, autumn and winter.
a) True
b) False
2.- Teher is more rain in January than in June
a) True
b) False
3.- The wet season is colder than the dry season
a) True
b) False
4.- It hardly ever rains in central Madagascar
a) True
b) False
5.- The wettest part of the island is the east.
a) True
b) False
3.2
Uso de la grámatica
3.1
Presentations
Como respondes a la pregunta: How are you?
a) I am 20 years old
b) I am very well
c) I am from Morelia
d ) I live in Mexico
e) You are very good
Solución .
Respuesta: Inciso B. Ya que la pregunta habla sobre un estado actual hacia la persona,
que es lo que le da seguimiento a la respuesta, dando una idea positiva sobre la información requerida.
3.2
Presentations
Como respondes a la pregunta: Where is she from?
a) She is a doctor
b) She is fine
c) She is from Italy
d ) She likes to eat
e) She is 28 years old
Solución .
Respuesta: Inciso C. Ya que la pregunta se refiere al lugar de donde ella es originaria, en
este caso, la respuesta hace referencia a Italia, lo cual ya es locación.
3.3
Presentations
Como respondes a la pregunta: Are you a student?
a) Yes I am
b) I am from france
c) I don´t like school
d ) Yes, I am not
e) I like to study
Solución .
Respuesta: Inciso A. Ya que la pregunta hace referencia a lo que se dedica la persona, en
este caso a ser un estudiente, la respuesta confirma la información que hay en la pregunta.
3.4
Presentations
Como respondes a la pregunta: What do you do?
a) I am a doctor
b) I ate pizza
c) I have homework
d ) I am playing
e) I have eaten
Solución .
Respuesta: Inciso A. La pregunta busca obtener información sobre a qué se dedica la
persona, la respuesta nos dice que la persona tiene como actividad principal el ser doctor.
3.5
Presentations
Como respondes a la pregunta: What does he usually do on weekends?
a) He visited his grandmother
b) He works with his father
c) He do his homework
d ) He study
c) He worked
Solución .
Respuesta: Inciso B.La pregunta busca información sobre la que la persona hace regu-
larmente en momentos específicos, como los son los fines de semana, tomando en cuenta que la pregunta se refiere a una tercera persona, lo cual es importante identificar, ya
que eso afecta directamente la estructura gramatical. La respuesta seleccionada nos da
la información solicitada incluyendo la gramática correcta.
3.6
Presentations
Como respondes a la pregunta: What did they do yesterday?
a) They do their homework
b) They studied for their exams
c) They drink coffee
d ) They work
e) They didn´t play
Solución .
Respuesta: Inciso B. La pregunta hace un cambio en el tiempo de la información que
se está solicitando, en este caso, la información debe estar en pasado, por lo tanto la
respuesta también debe estarlo. La respuesta seleccionada es la única que nos da la estructura correcta de acuerdo a la pregunta.
3.7
Presentations
Como respondes a la pregunta: What does she like doing in the evenings?
a) She likes eating her breakfast
b) She likes reading books
c) She enjoys to have dinner
d ) She enjoy having dinner
e) She liked eating dinner
Solución .
Respuesta: Inciso B. La pregunta busca obtener información sobre las actividades que
le gustan hacer a la persona en un momento especifico del día, lo cual requiere que la
respuesta esté diseñada para dar información que vaya de acuerdo al tiempo que se está
usando.
3.8
Presentations
Como respondes a la pregunta: Has she ever played soccer?
a) Yes, she have played soccer
b) No, she haven´t play soccer
c) Yes, she has played soccer
d ) Yes, she did
e) No, she didn´t
Solución .
Respuesta: Inciso C. La estructura de la pregunta requiere que la respuesta esté usando
el mismo tiempo gramatical (Present perfect), la respuesta seleccionada hace referencia
al tiempo requerido tomando en cuenta que también se debe respetar el uso de la tercera
persona para su correcta aplicación.
3.9
Presentations
Como respondes a la pregunta: What would you do if you won the lottery?
a) I will buy a house and a car
b) I should invest my money
c) I would travel around the world
d ) I can travel around the world
e) I won´t do anything
Solución .
Respuesta: Inciso C. La pregunta hace referencia a una situación irreal, lo cual requiere
que la respuesta use una estructura específica que solamente se usa en las condicionales.
3.10
Presentations
Como respondes a la pregunta: When was the TV invented?
a) The TV was invented in 1922
b) The TV is invented in 1922
c) The TV were invented in 1922
d ) The TV wasn´t invented
e) The TV were invented in 1922
Solución .
Respuesta: Inciso A. La pregunta hace referencia a una acción pasada usando la estructura de Passive voice, este tema requiere una estructura gramatical específica para poder
ser usado. La respuesta seleccionada respeta las características del tema y responde a la
pregunta con la información solicitada.
3.2.1
Ejercicios
Choose the best option to complete the sentence.
1. ... you watching TV at the moment?
a) Are
b) Is
c) Will
b) goed
c) went
2. She ... out lastnight
a) go
3. How often ... your mum clean the house?
a) do
b) does
c) is
4. I think you ... go to the doctor
a) are
b) should
c) has to
b) haven´t
c) don´t
5. My boss ... called me yet
a) hasn´t
6. My dad came home when I ...
a) were doing exercise
b) am doing exercise
c) was doing exercise
b) never
c) every day
7. I ... smoke, I hate it
a) always
8. Since Laura visited me, I ... very sad
a) has been
b) had been
c) have been
b) did never thought
c) would have never thought
9. What a great idea! I ...
a) has never thought
85
Parte II
Examen Diagnóstico
4
Matemáticas
Aritmética
Números naturales.
El ser humano ha tenido la necesidad de contar prácticamente desde su aparición hasta hoy,
para satisfacer dicha necesidad hizo uso de los números, 1, 2, 3, 4, 5, ..., los cuales llamó números naturales, en este conjunto de números no se contempla el cero ni los números negativos,
ya que por naturaleza el ser humano esta asociado a ellos.
Operaciones con números enteros
Suma y Resta.
Números con signos iguales se suman y al resultado se le coloca el signo de los sumandos.
4.1
Suma aritmética
1) −4 − 5 − 9 = −18
2) 2 + 8 + 13 = 23
3) −11 − 6 − 7 = −24
Cuando los números tienen signos diferentes, estos se restan y al resultado se le coloca el signo
del número mayor en valor absoluto.
4.2
Suma aritmética
1) −13 + 9 = −4
2) −6 + 7 + 9 − 11 = 16 − 17 = −1
3) 7 − 21 + 4 + 23 − 9 = 34 − 30 = 4
Leyes de los signos.
Multiplicación
(+)(+) = +, (+)(−) = −, (−)(+) = − y (−)(−) = +
Matemáticas
4.1
86
División
+
+
= +,
+
−
= −,
−
−+ = − y −
=+
Multiplicación y división.
Se aplican las leyes de los signos y se realiza la operación con los coeficientes.
4.3
Multiplicación y división
1) (−7)(6) = −42
2) (−2)(−15) = 30
3) (3)(−5) = −15
4) −21
3 = −7
−105
5) −7 = 15
143
= −11
6) −13
Números Reales.
Los números reales son todos los números que pueden representarse en la recta numérica.
Los números reales, también pueden clasificarse de acuerdo a los siguientes conjuntos de números.
p
Racionales (Q). Son los números de la forma q , donde p, q son números enteros y q ̸= 0, también se le conocen como fracciones comunes.
Ejemplos:
4
3
5 , − 2 , 1.3
Naturales (N).Son aquellos números que se utilizan para contar y su conjunto es: N = {1, 2, 3, 4, ...}.
Números primos. Son los números que solo pueden dividirse entre la unidad y el propio número y obtener como resultado un número entero: {2, 3, 7, 11, 13, 17, 19, ...}.
Números compuestos. Son números que tienen más de 2 divisores: {4, 6, 8, 9, 10, |2, ...}.
Números enteros(Z). Su conjunto se conforma de números positivos, negativos y el cero:
{..., −3, −2, −1, 0, 1, 2, 3, ...}.
Irracionales (Q’). Son todos aquellos números cuya parte decimal se conforma de una serie
infinita de
dígitos, pero no existe periodo y por lo regular son resultado de raíces no exactas:
p
p
π, 2, π2 , 43 .
Notación científica.
En varias áreas de la ciencia, usualmente se trabajan con números grandes o pequños derivados de alguna operación o medición de algún suceso. Estos números pueden ser representados
de manera sencilla y cómoda usando criterios de redondeo de números y múltiplos de diez, lo
cual se conoce como notación científica.
Los múltiplos de diez, pueden representarse expresando diez elevado a una potencia (exponente) positiva.
4.4
Notación científica
100 = 10 ∗ 10 = 102
1000 = 10 ∗ 10 ∗ 10 = 103
1000000 = 10 ∗ 10 ∗ 10 ∗ 10 ∗ 10 ∗ 10 = 106
Las fracciones de diez (o submúltiplos) se representan en forma semejante, la única diferencia
que en éste caso se utilizan exponentes negativos.
1
10
= 0.1−1
1
100
= 0.1−2
1
100000
= 0.1−6
La notación científica tiene la siguiente forma:
a.b ∗ 10±n con dos cifras significativas
a.bc ∗ 10±n con tres cifras significativas
a.bcd ∗ 10±n con cuatro cifras significativas
4.5
Escribe en forma de notación normal
1) 3.2 ∗ 105 = 320, 000
2) 3.57 ∗ 10−4 = 0.000357
3) 1.18 ∗ 10−3 = 0.00118
4.6
Escribe en forma de notación científica.
1) 5, 265, 000 = 5.265 ∗ 106
2) 0.000956 = 9.56 ∗ 10−4
3) 518, 000 = 5.18 ∗ 105
4.2
Algebra
Expresiones algebraicas.
Término algebraico.
Es la expresión que se utiliza para generalizar una cantidad, también se le denomina monomio
y sus elementos son: coeficiente(s), base(s) y exponente(s).
4.7
Término algebraico
Término
x
2m 2
−4x 2 y 5
1
2
3 ab
Coeficiente
1
2
−4
1
3
Base(s)
x
m
x, m
a, b
Exponente(s)
1
3
2, 5
1, 2
Término semejante.
Son términos cuyas bases son iguales y están elevadas a los mismos exponentes.
4.8
Término semejante
Términos semejantes
3x con 5x
5x 2 y 3 con −x 2 y 3
3 2
3
2
3
2 m np con −3m np
No son términos semejantes
3x con 5x 2
5x 2 y 3 con 5x 2 y
3 2
3
2 3
2 m np con −3m n p
Reducción de términos semejantes. Si se suman o restan dos o más términos semejantes, únicamente se realizan las operaciones con los coeficientes y queda la misma base en el resultado.
En la suma o resta de términos semejantes NO se alteran los exponentes de las bases.
4.9
Reducción de términos semejantes
1) Reduce la siguiente expresión 5x + 9x − 12x − 4x:
Solución .
5x + 9x − 12x − 4x = (5 + 9 − 12 − 4)x = (14 − 16)x = −2x
4.10
Reducción de términos semejantes
2) Reduce la siguiente expresión 5x 2 − 6x + 9x 2 + 2x es:
Solución .
5x 2 − 6x + 9x 2 + 2x = (5 + 9)x 2 + (−6 + 2)x = 14x 2 − 4x
4.11
Reducción de términos semejantes
3) Reduce la siguiente expresión 3x 2 + 5x + y?7x 2 − x + 7y es
Solución .
3x 2 + 5x + y?7x 2 − x + 7y = (3 − 7)x 2 + (5 − 1)x + (1 + 7)y = −4x 2 + 4x − 8y
Polinomio
Un polinomio es el resultado de sumar o restar 2 o más términos algebraicos no semejantes; en
específico, será binomio si son 2 términos algebraicos y trinomio si son 3 términos.
Expresión algebraica
3x − 5y
2
a ± 2ab + b 2
Nombre
Binomio
Trinomio
Suma de polinomios. Al sumar 2 o más polinomios se simplifican los términos semejantes entre
los polinomios.
4.12
Suma de polinomios
1) El resultado de (4a 2 − 5a + 7) + (−2a 2 + 3a − 4) es:
Solución .
Para darle solución, se recomienda acomodar los términos semejantes en forma vertical
y se respetan los signos de los términos algebraicos que forman cada uno de los polinomios. Se procede a la simplificación de los términos algebraicos.
4a 2 − 5a + 7
−2a 2 + 3a − 4
———————–
2a 2 − 2a + 3
4.13
Suma de polinomios
2) La suma de 8x + 7y − 11 con −5y + 12x − 2 + 3z es:
Solución .
Para darle solución, se recomienda acomodar los términos semejantes en forma vertical
y se respetan los signos de los términos algebraicos que forman cada uno de los polinomios. Se procede a la simplificación de los términos algebraicos.
8x
12x
20x
4.14
+7y
−5y
+2y
−11
−2
−13
+3z
+3z
Sustracción de polinomios
3) La sustracción de 25 x 2 − x y + 13 y 2 a 2x 2 + 3x y + 14 y 2 es:
Solución .
Para darle solución, se recomienda acomodar los términos semejantes en forma vertical
y se respetan los signos de los términos algebraicos que forman el primer polinomio,
cambiando el signo a todos los términos que forman el segundo polinomio. Se procede
a la simplificación de los términos algebraicos.
2 2
x
5
−x y
1
+ y2
3
−2x 2
−3x y
1
− y2
4
8
− x2
5
−4x y
−
1 2
y
12
Multiplicación de polinomios. Para realizar esta operación se consideran la regla de los signos
en multiplicación y la ley de los exponentes para el producto de bases iguales.
4.15
Multiplicación de polinomios
1) (x 6 )(x 2 ) = x 6+2 = x 8
2) (−3x 2 y 3 )(4x y 2 ) = (3)(4)(x 2+1 )(y 3+2 ) = 12x 3 y 5
3) 2x 2 (x 2 + 3x − 4) = (2x 2 )(x 2 ) + (2x 2 )(3x) + (2x 2 )(4) = 2x 4 + 6x 3 − 8x 2
División de polinomios. Para realizar esta operación se consideran las leyes de los signos para
la división y la de los exponentes para la división de bases iguales
4.16
1)
2)
3)
4.2.1
División de polinomios
−108x 6
6−2
= 9x 4
= −108
−12 x
−12x 2
3 5
12x y
12 3−2 5−3
x
y
= −3x y 2
= −4
−4x 2 y 3
3 5 2
18a b c
18 3−2 5−5 2
= −4
a b c = − 92 5ab 0 c 2
10a 2 b 5
= − 92 ac 2
Métodos para la representación de lugares geométricos; ecuaciones lineales y cuadráticas.
Definición 4.1
Línea recta
Es el lugar geométrico de todos los puntos tales que si se toman 2 cualesquiera, el valor
de la pendiente es constante. Existen dos fórmulas para obtener la ecuación de una línea
recta.
Ecuación de la línea recta
Punto-pendiente. Para hallar la ecuación de la recta que pasa por el punto P 1 (x 1 , y 2 ) y tiene
pendiente m, se utiliza la siguiente fórmula:
y − y 1 = m(x − x 1 )
Dos puntos. Para determinar la ecuación de la recta que pasa por los puntos P 1 (x 1 , y 1 ) y P 2 (x 2 , y 2 ),
se utiliza la siguiente fórmula:
y − y1 =
y 2 −y 1
x 2 −x 1 (x − x 1 )
Formas de representar la ecuación de la recta.
General. Es la forma más común de representar la ecuación de una recta y se obtiene al igualar
a cero.
ax + b y + c = 0
Ordinaria. Con esta forma se determina la pendiente de la recta, así como la intersección de la
misma en el eje Y, se obtiene despejando la variable y de la ecuación general.
y = mx + b
4.17
Ecuaciones lineales y cuadráticas
1) La ecuación de la recta en su forma general que pasa por el punto (−2, 5) y tiene pendiente 13 es:
Solución .
Al utilizar la fórmula y − y 1 = m(x − x 1 ), se obtiene:
y − 5 = 31 (x − (−2))
→
3(y − 5) = 1(x + 2)
→
3y − 15 = x + 2
x + 2 − 3y + 15 = 0
→
x − 3y − 17 = 0
→
4.18
Ecuaciones lineales y cuadráticas
2) ¿Cuál es la ecuación de la recta en su forma general, que pasa por los puntos P 1 (2, −5)
y P 2 (−6, 3)?
Solución .
Se aplica la fórmula y − y 1 =
y − (−5) =
3−(−5)
−6−2 (x − 2)
y 2 −y 1
x 2 −x 1 (x − x 1 ).
→
8
y + 5 = −8
(x − 2)
x + y +3 = 0
→
y + 5 = −1(x − 2)
→
Graficación de rectas.
No existe un solo método para obtener la gráfica de una recta, para esta guía utilizaremos el
método de la forma ordinaria de la recta. En la siguiente imagen se explica brevemente los
elementos que deben tomarse en cuenta para graficar la recta.
Figura 1. Elementos a considerar para graficar una recta.
1) La gráfica de la recta y = 2x − 5, es:
La ecuación y = 2x − 5, tiene la forma ordinaria y = mx + b, entonces m = 2 y b = −5, es
necesario que la pendiente sea una fracción, por tanto la pendiente se puede expresar
como:
m=
3
Movimiento vertical
=
2 Movimiento horizontal
Se ubica la intersección con el eje y, el punto (0, b) = (0, −5)
Se grafica la pendiente a partir de la intersección realizando un movimiento horizontal y
tres verticales, como lo muestra la figura.
Por último, la gráfica de la recta es aquella que pasa por los puntos indicados.
2) La gráfica de la recta y = − 23 x + 2, es:
De acuerdo con la recta, el punto de intersección con el eje y es (0, 2) y la pendiente
m = −3
2 .
Ecuaciones cuadráticas.
Parábola.
Se define como el lugar geométrico de los puntos del plano, cuya distancia a un punto fijo,
llamado foco, es la misma distancia que existe a una recta fija llamada directriz y se obtiene a
partir de una ecuación cuadrática.
Donde: P F = P D
V : Vértice
F : Foco
DD ′ : Directríz
LR : Lado recto, LR = |4p|
p : parámetro (distancia del vértice al foco o a la directriz)
Elementos y ecuación de una parábola con vértice en el origen
Parábola horizontal.
Su foco está sobre el eje X y son cóncavas hacia la derecha o a la izquierda.
Ecuación canónica:
y 2 = 4px
Foco: F (p,³ 0) ´
Directriz DD ′ : x = −p
Ecuación del
´ y =0
³ eje:
Lado recto LR = |4p|
Si p > 0 entonces la parábola abre hacia la derecha.
Si p < 0 entonces la parábola abre hacia la izquierda.
Parábola vertical.
Su foco está sobre el eje Y , son cóncavas hacia arriba o hacia abajo.
Ecuación canónica:
x 2 = 4p y
Foco: F (0,³ p) ´
Directriz DD ′ : y = −p
Ecuación del
³ eje:
´ x =0
Lado recto LR = |4p|
Si p > 0 entonces la parábola cóncava hacia arriba.
Si p < 0 entonces la parábola cóncava hacia abajo.
4.19
Parábola vertical
Obtén la gráfica y ecuación de la parábola con vértice en el origen y foco en el punto
(−4, 0).
Solución .
Ubicamos a los elementos dados en el plano cartesiano, por los elementos dados podemos deducir que la parábola es cóncava hacia la izquierda y el valor del parámetro es
p = −4, al sustituir en la ecuación y 2 = 4px, obtenemos:
y 2 = 4px y 2 = 4(−4)x y 2 = −16x y 2 + 16x = 0
Elementos y ecuación de una parábola con vértice en (h, k).
Parábola horizontal.
Su eje es paralelo al eje X y es cóncava hacia la derecha o izquierda.
Donde: Ecuación ordinaria:
(y − k)2 = 4p(x − h)
Ecuación general: C y 2 + D x + E y + F = 0
Vértice: V (h, k)
Foco: F (h³+ p, k)
´
Directriz DD ′ : x = h − p
Eje: y = k ³ ´
Lado recto LR = |4p|
Si p > 0 entonces la parábola cóncava hacia la derecha.
Si p < 0 entonces la parábola cóncava hacia la izquierda.
Parábola vertical.
Su eje es paralelo al eje Y , y es cóncava hacia arriba o abajo.
Donde: Ecuación ordinaria:
(x − h)2 = 4p(y − k)
Ecuación general: Ax 2 + D x + E y + F = 0
Vértice: V (h, k)
Foco: F (h,³ k + p)
´
Directriz DD ′ : y = k − p
Eje: x = h ³ ´
Lado recto LR = |4p|
Si p > 0 entonces la parábola cóncava hacia arriba.
Si p < 0 entonces la parábola cóncava hacia abajo.
4.20
Parábola vertical
La directriz de una parábola es la recta y − 1 = 0, y su foco es el punto (4, −3), encuentra
su ecuación y gráfica.
Solución .
Al relacionar las fórmulas de los elementos de la parábola vertical con los datos, se obtienen las coordenadas del vértice y el valor del parámetro.
Foco: F (h, k + p) = F (4, −3)
→
h = 4 y k + p = −3
Directriz:
Como y = k − p
Se sabe que y − 1 = 0
Por lo tanto: k − p − 1 = 0
→
k −p =1
Resolvemos un pequeño sistema de ecuaciones:
k + p = −3
k −p =1
La solución es:
h = 4, k = 1, p = −2
Las coordenadas del vertice son V (4, 1) y el parámetro p = −2
Se sustituye el vértice y el parámetro en:
(x − h)2 = 4p(y − k)
(x − 4)2 = 4(−2)(y + 1)
Se desarrollan las operaciones y se simplifica para obtener la siguiente expresión:
x 2 − 8x + 8y + 24 = 0
1.5 Operaciones básicas con fracciones algebraicas.
Simplificación de fracciones.
Simplificar una fracción algebraica es representarla en su forma más simple al aplicar los métodos de factorización.
4.21
Operaciones básicas con fracciones algebraicas
1) Simplifica la expresión
Solución .
x 2 −25
=
x 2 +7x+10
4.22
(x+5)(x−5)
(x+5)(x+2)
=
x 2 −25
x 2 +7x+10
(x−5)
(x+2)
Operaciones básicas con fracciones algebraicas
2) Simplifica la expresión
x 2 −6x+8
x−4
Solución .
x 2 −6x+8
= (x−4)(x−2)
= x −2
x−4
(x−4)
4.23
Operaciones básicas con fracciones algebraicas
3) Simplifica la expresión
Solución .
2x 2 +3x+1
=
x 2 +3x+2
(2x+1)(x+1)
(x+2)(x+1)
=
2x 2 +3x+1
x 2 +3x+2
(2x+1)
(x+2)
1.6 Leyes de los exponentes y radicales.
Potencia.
Es la representación del producto de una base por sí misma, un cierto número de veces.
a n = a ∗ a ∗ a ∗ a...
Donde a es la base y n el exponente.
Propiedades de los exponente:
Si a, b, m, n ∈ R y a, b ̸= 0, entonces:
a m ∗ a n = a m+n
4.24
Propiedades de los exponentes
1) ¿Cuál es el resultado de x 4 ∗ x 7
Solución .
x 4 ∗ x 7 = x 4+7 = x 11
4.25
Propiedades de los exponentes
2)Encuentra el resultado de (−3y 2 )(5y)(−11y 13 )
Solución .
(−3y 2 )(5y)(−11y 13 ) = 165y 2+1+13 = 165y 16
Si se trata de división.
am
= a m−n
an
4.26
Propiedades de los exponentes
1) ¿Cuál es el resultado de
x4
x7
Solución .
x4
= x 4−7 = x −3
x7
4.27
Propiedades de los exponentes
2) Encuentra el resultado de
Solución .
−3y 7
3 7−3
y
=
= 11
−11y 3
−3y 7
−11y 3
3 4
11 y
Cuando se trata de un exponente igual a cero.
a0 = 1
4.28
Propiedades de los exponentes
1) ¿Cuál es el resultado de (−7x 5 )0
Solución .
(−7x 5 )0 = 1
Un exponente elevado a otro exponente.
(a n )m = a m∗n
4.29
Propiedades de los exponentes
1) ¿Cuál es el resultado de (x 5 )7
Solución .
(x 5 )7 = x 5∗7 = x 35
Producto de diferentes bases elevadas a un exponente.
(a ∗ b ∗ c)n = a n ∗ b n ∗ c n
4.30
Propiedades de los exponentes
1) ¿Cuál es el resultado de (x ∗ y ∗ z)7
Solución .
(x ∗ y ∗ z)7 = x 7 ∗ y 7 ∗ z 7
4.31
Propiedades de los exponentes
2) ¿Cuál es el resultado de (x 3 ∗ y 2 ∗ z)7
Solución .
(x 3 ∗ y 2 ∗ z)7 = x 7∗3 ∗ y 7∗2 ∗ z 7∗1 = x 21 ∗ y 14 ∗ z 7
Fracción elevada a un exponente.
³ a ´n
b
4.32
=
an
bn
Propiedades de los exponentes
1) ¿Cuál es el resultado de
Solución
³ 2 4 ´3 . 2∗3 4∗3
x ∗y
x ∗y
= z 5∗3 =
z5
³
´
x 2 ∗y 4 3
z5
x 6 ∗y 12
z 15
Radical.
La expresión
p
n
a recibe el nombre de radical y se define como:
p
n
a = b si y sólo si b 2 = a
Elementos de un radical.
Un radical es una expresión algebraica, que se forma con los siguientes elementos: coeficiente,
radicando e índice de raíz
4.33
Propiedades de los exponentes
Ejemplo
p
2 3
p
3
2x y
p
4
5x 3x 2 y
Coeficiente
2
1
5x
Radicando
3
2x y
3x 2 y
Índice de raíz
2
3
4
Cuando un radical esta elevado a un exponente, el radical se expresa como exponente fraccionario y se multiplican los exponentes:
p
n
4.34
p
m
a m = ( n a)m = a n
Propiedades de los exponentes
1) Expresa el exponente en forma de fracción
p
5
z4
Solución
.
p
4
5
z4 = z 5
4.35
Propiedades de los exponentes
2) Expresa el exponente en forma de fracción
p
x3
Solución
.
p
3
x3 = x 2
4.36
Propiedades de los exponentes
3) Expresa el exponente en forma de fracción
p
4
(x 2 + 2y)3
Solución .
p
3
4
(x 2 + 2y)3 = (x 2 + 2y) 4
Los teoremas de los exponentes también se aplican a los radicales, ya que se expresan como
exponentes fraccionarios.
p
n
a ∗b ∗c =
p
n
a∗
p
p
n
b∗ n c
4.37
Propiedades de los exponentes
1) Expresa el exponente en forma de fracción
p
5
2z 4 y
Solución .
p
p
p
p
5
5
5
2z 4 y = 2 ∗ z 4 ∗ 5 y
r
n
4.38
p
n
a
a
= p
n
b
b
Propiedades de los exponentes
1) Expresa el exponente en forma de fracción
p
5
2z 4 y
Solución
.
q
p
5
3x
5 3x
p
y = 5y
El radical de un radical.
q
n
p
m
x=
1) Expresa el exponente en forma de fracción
p
n∗m
a
p
4 p
5
2z
p
p
p
4 p
5
3∗5
15
2z =
2z = 2z
4.3
Geometría
Paralelismo, congruencia, semejanza (teorema de Tales) y rectas (mediatriz y bisectriz)
Paralelismo.
Dos rectas son paralelas si no tienen un punto en común y guardan siempre una misma distancia. Por ejemplo, las rectas AB y C D son paralelas y se escribe AB ||C D.
Congruencia.
Dos triángulos son congruentes si tienen la misma forma y el mismo tamaño:
a) Sus lados correspondientes son iguales.
b) Sus ángulos correspondientes son iguales.
Por ejemplo los siguientes triángulos son congruentes, porque tienen iguales tanto sus lados
correspondientes como sus ángulos correspondientes.
4.39
Semejantes
Los triángulos ABC y A?B ?C ? son semejantes. Encuentra el valor de b y c.
Solución .
a) x = 4, y = 11◦
b) x = 4, y = 48◦
d ) x = 2, y = 1◦
c) x = 33, y = 48◦
e) x = 5, y = 4◦
Como los triángulos son congruentes se tiene que los lados y ángulos correspondientes
son iguales. Entonces:
3y + 15◦ = 48◦ → 3y = 48◦ − 15◦ → 3y = 33◦ → y = 11◦
x
x
x
+6 = x +4 → 6−4 = x − → 2 = → x = 4
2
2
2
Por lo cual, la respuesta correcta es el inciso a.
Semejanza.
Dos triángulos son semejantes si tienen la misma forma, pero no el mismo tamaño:
a) Sus ángulos correspondientes son iguales.
b) Sus lados correspondientes son proporcionales:
b
c
a
= ′= ′
′
a
b
c
Por ejemplo los siguientes triángulos son semejantes, porque tienen iguales sus ángulos correspondientes y sus lados correspondientes son proporcionales, es decir:
8 6 10
= =
=2
4 3
5
4.40
Semejanza
Los triángulos ABC y A′B ′C ′ son semejantes. Encuentra el valor de b y c.
Solución .
a) b = 14, c = 10
b) b = 4, c = 8
d ) b = 11, c = 10
c) b = 12, c = 15
e) b = 1, c = 12
Como los triángulos son semejantes se tiene que los lados correspondientes son proporcionales
9 b c
= =
3 4 5
por lo que se obtiene
c 9
=
5 3
b 9
=
4 3
→
→
9·5
= 15
3
9·4
b=
= 12
3
c=
La respuesta correcta es el inciso c
Teorema de Tales.
Cuando en un triángulo se traza una recta paralela a uno de los lados, el triángulo que se forma
es semejante al primero.
4.41
Teorema de Tales
En el siguiente triángulo determina el valor de x, si DE ||BC .
Solución .
a) x = 10
b) x = 14
d ) x = 42
c) x = 12
e) x = 24
Por el Teorema de Tales los triángulos ∆ABC y ∆ADE son semejantes. Por la proporcio-
nalidad de los lados se tiene que
x + 12 28 + 14
=
12
14
Y al resolviendo para x
x + 12 42
=
12
14
→
x + 12 =
12 · 42
14
→
x=
12 · 42
− 12
14
→
x = 24
La respuesta correcta es el inciso e.
Mediatriz
La mediatriz es una recta perpendicular a un segmento y que además pasa por su punto medio.
4.42
Mediatriz
Encuentra la ecuación de la mediatriz del segmento de recta cuyos extremos son los puntos P (−3, 0) y Q(1, 1).
a) y = −4x − 7
b) y = 2x − 4
d ) y = −4x −
7
2
c) y = 4x +
e) y = 4x −
7
2
7
2
Solución .
Usando las coordenadas x 1 = −3, y 1 = 0 del punto P y x 2 = 1, y 2 = 1 del punto Q se obtienen el punto medio P m y la pendiente m del segmento PQ
¶
µ
³x +x y + y ´
−3 + 1 0 + 1
1
2
1
2
Pm = Pm
,
= Pm
,
= P m (−1, 1/2)
2
2
2
2
m=
1−0
y2 − y1
=
= 1/4
x 2 − x 1 1 − (−3)
Para obtener la pendiente m 1 de la mediatriz se usa la condición de ortogonalidad entre
la mediatriz y el segmento de recta m 1 · m = −1 para tener
m 1 · (1/4) = −1 → m 1 = −4
Por lo cual, usando la ecuación punto-pendiente, se obtiene la ecuación de la mediatriz
que se busca
y−
1
1
7
= −4(x − (−1)) → y − = −4x − 4 → y = −4x −
2
2
2
La respuesta correcta es el inciso d .
4.4
Cálculo de perímetros y áreas de figuras planas
A continuación se presentan ejemplos de cálculo de perímetros y áreas de algunas figuras planas.
Trapecios.
Perímetro. El perímetro se define como la suma de los lados del trapecio.
Área. Es el semiproducto de la suma de la base mayor y base menor por la altura.
4.43
Trapecios
Encuentra el área de un trapecio isósceles si su perímetro es de 32 cm, sus lados iguales
miden 5 cm y la altura 3 cm.
a) A = 33 cm
b) A = 11 cm
d ) A = 56 cm
c) A = 23 cm
e) A = 66 cm
Solución .
Como se conoce la altura, resta encontrar la suma de las bases mayor y menor. De la
fórmula del perímetro, recordando que el trapecio es isósceles con dos lados iguales a c,
se tiene que
P = a +b +c +c
Al sustituir los valores conocidos del perímetro y los lados iguales se tiene
32 = a + b + 5 + 5 → a + b = 32 − 5 − 5 → a + b = 22
Por lo cual, al sustituir en la fórmula del área se tiene el resultado pedido
A=
(a + b)h 22 · 3
=
= 33 cm
2
2
La respuesta correcta es el inciso a.
Polígonos regulares.
Perímetro. El perímetro se define como el producto del número de lados por la medida de cada lado del polígono regular.
Apotema. Es la longitud del segmento que une el centro del polígono y el punto medio de uno
de los lados.
Área. Es el semiproducto del perímetro por la apotema.
4.44
Polígonos regulares
¿Cuál es el perímetro y área de un pentágono regular de lado igual a 4 m y apotema igual
a 3 m?
a) P = 20 m 2
b) P = 40 m 2
d ) P = 10 m 2
c) P = 30 m 2
e) P = 45 m 2
Solución .
P = 5(4) = 20 m y A =
20 · 3
= 30 m 2
2
La respuesta correcta es el inciso c.
4.5
Figuras geométricas: perímetro, área y volumen
Se presenta a continuación ejemplos de cálculos de área total y volumen de algunas figuras
geométricas.
Cilindro circular recto.
Área lateral: Producto del perímetro de la base y la altura del cilindro.
Área total: La suma del área lateral y las áreas de la base y tapa.
Volumen: Producto del área de la base y la altura.
4.45
Cilindro circular recto
¿Cuál es el área lateral, área total y el volumen de un cilindro con radio de la base igual a
3 cm y con altura de 6 cm?
a) A L = 14π cm 2 , A T = 40π cm 2 , V = 25π cm 3
b) A L = 36π cm 2 , A T = 54π cm 2 , V = 54π cm 3
c) A L = 44π cm 2 , A T = 50π cm 2 , V = 52π cm 3
d ) A L = 16π cm 2 , A T = 14π cm 2 , V = 15π cm 3
e) A L = 6π cm 2 , A T = 4π cm 2 , V = 5π cm 3
Solución .
Área lateral: A L = 2πr h = 2π(3)(6) = 36π cm 2
Área total: A T = 2πr h + 2πr 2 = 36π + 2π(3) = 36π + 18π = 54π cm 2
Volumen: V = πr 2 h = π(3)2 (6) = 54π cm 3
La respuesta correcta es el inciso b.
4.6
Pendiente de la recta y ángulo entre rectas
La pendiente de una recta se define como la tangente del ángulo de inclinación y se denota
por la letra m :
m = tan θ
Si una recta L pasa por los puntos P 1 (x 1 , y 1 ) y P 2 (x 2 , y 2 ) la pendiente se calcula por la fórmula
m=
y2 − y1
x2 − x1
4.46
Pendiente
¿Cuál es la pendiente de la recta que pasa por los puntos P (1, 4) y Q(7, −3) ?
a) m = 1
d)m =
b) m =
8
3
11
10
e) m = −
c) m = −
1
5
7
6
Solución .
Al usar la fórmula anterior, con x 1 = 1, y 1 = 4 para P y x 2 = 7, y 2 = −3 para Q se tiene que
m=
−3 − 4
7
=−
7−1
6
La respuesta correcta es el inciso e.
El ángulo θ entre dos rectas con pendientes m 1 y m 2 respectivamente se define por la fórmula
tan θ =
4.47
m2 − m1
1 + m1 · m2
Pendiente
¿Cuál es la medida del ángulo agudo que forman las rectas cuyas pendientes son 2 y −3 ?
a) θ = 40◦
b) θ = 45◦
d ) θ = 35◦
c) θ = 20◦
e) θ = 60◦
Solución .
Al usar la fórmula correspondiente, con m 1 = 2, m 2 = −3 se tiene que
tan θ =
−3 − 2
−5
−5
=
=
=1
1 + 2 · (−3) 1 − 6 −5
Aplicando tangente inversa se tiene
θ = arctan(1) = 45◦
La respuesta correcta es el inciso b.
4.7
Ecuaciones y gráficas de la circunferencia, la parábola, la elipse y la hipérbola
Circunferencia
Una circunferencia es el lugar geométrico del plano cartesiano que describe un punto P moviéndose de manera que su distancia (radio r ) a un punto fijo (centro C ) siempre es constante.
Ecuación ordinaria: Ecuación de la circunferencia con centro en el punto con coordenadas
C (h, k) y radio r :
(x − h)2 + (y − k)2 = r 2
Ecuación general: Si se desarrollan los binomios de la ecuación ordinaria y se iguala a cero se
obtiene la ecuación general:
Ax 2 + B y 2 + D x + E y + F = 0
4.48
Ecuaciones y gráficas de la circunferencia
Determina la ecuación ordinaria y general de la circunferencia con centro en C (2, −3) y
radio r = 5.
a) 2x 2 + 2y 2 − 6x + 4y − 12 = 0
b) x 2 + y 2 − 12 = 0
d ) x 2 + y 2 − 25 = 0
c) x 2 + y 2 − 4x + 6y − 12 = 0
e) x 2 + y 2 − x + y − 12 = 0
Solución .
Sustituyendo h = 2, k = −3 y r = 5 en la fórmula para la ecuación ordinaria se obtiene
(x − 2)2 + (y − (−3))2 = 52
(x − 2)2 + (y + 3)2 = 25
Al desarrollar los binomios e igualar a cero obtenemos para la ecuación general
x 2 − 4x + 4 + y 2 + 6y + 9 = 25
x 2 − 4x + 4 + y 2 + 6y + 9 − 25 = 0
x 2 − 4x + y 2 + 6y − 12 = 0
x 2 + y 2 − 4x + 6y − 12 = 0
La respuesta correcta es el inciso c.
Parábola
Una parábola es el lugar geométrico del plano cartesiano que describe un punto P que se mueve de tal forma que equidista de un punto fijo F llamado foco, y una recta fija, llamada directriz.
Ecuación ordinaria de la parábola con vértice en el origen:
x 2 = 4p y parábola vertical
y 2 = 4px parábola horizontal
Ecuación ordinaria de la parábola con vértice en el punto: (h,k)
(x − h)2 = 4p(y − k) parábola vertical
(y − k)2 = 4p(x − h) parábola horizontal
4.49
Parábola
Encuentra la ecuación general de la parábola cuyo vértice tiene coordenadas (−4, 3) y su
foco tiene coordenadas (−1, 3) respectivamente.
a) x 2 − 12x − 6x − 39 = 0
b) y 2 − x − y − 9 = 0
d ) y 2 − 12x − 6y − 39 = 0
c) 3y 2 + 2x − 39 = 0
e) x 2 − 6x − 12y − 9 = 0
Solución .
Al graficar los puntos dados se observa que la parábola es horizontal (su eje es paralelo
al eje de las "x") y abre a la derecha. Al sustituir los valores h = −4, y = 3 y p = 3 se tiene
la ecuación ordinaria
(y − 3)2 = 4(3)(x − (−4))
(y − 3)2 = 12(x + 4)
Desarrollando los productos e igualando a cero se obtiene la fórmula general
y 2 − 6y + 9 = 12x + 48
y 2 − 6y + 9 − 12x − 48 = 0
y 2 − 12x − 6y − 39 = 0
La respuesta correcta es el el inciso d .
Elipse
Una elipse es el lugar geométrico del plano cartesiano que describe un punto P que se mueve
de tal forma que la suma de sus distancias a dos puntos fijos F 1 y F 2 , llamados focos, es constante.
Ecuación ordinaria de la elipse con centro en el origen:
x2 y 2
+
= 1 elipse vertical
b2 a2
x2 y 2
+
= 1 elipse horizontal
a2 b2
Ecuación ordinaria de la elipse con centro en el punto: (h,k)
(x − h)2 (y − k)2
+
= 1 elipse vertical
b2
a2
(x − h)2 (y − k)2
+
= 1 elipse horizontal
a2
b2
4.50
Elipse
Encuentra la ecuación general de la elipse de centro en el origen, vértice (0, 5) y foco en
(0, 4).
a) 25x 2 + 9y 2 − 225 = 0
b) 5x 2 + 3y 2 − 225 = 0
d ) 9x 2 + 25y 2 − 225 = 0
c) 3x 2 + 5y 2 − 25 = 0
e) x 2 + y 2 − 225 = 0
Solución .
Al graficar los puntos dados se observa que la elipse es vertical y que las distancias del
centro al vértice y al foco son respectivamente
a = 5, c = 4.
Al usar la condición a 2 + b 2 = c 2 se obtiene para b :
p
p
p
p
b = c 2 − a 2 = 52 − 42 = 25 − 16 = 9 = 3.
Al sustituir los valores de a y b en la ecuación ordinaria tenemos
x2 y 2
+
= 1.
9 25
Si se multiplica por 225 (para eliminar denominadores) e igualar a cero se obtiene la
ecuación general
25x 2 + 9y 2 = 225
25x 2 + 9y 2 − 225 = 0
La respuesta correcta es el inciso a.
4.8
Cálculo diferencial
La aparición del análisis infinitesimal fue la culminación de un largo proceso, cuya esencia matemática interna consistió en la acumulación y asimilación teórica de los elementos del cálculo
diferencial. Las causas que motivaron este proceso fueron las exigencias de la mecánica newtoniana y la astronomía.
La última etapa del desarrollo del análisis infinitesimal fue el establecimiento de la relación e
inversibilidad mutua entre las investigaciones diferenciales, y a partir de aquí la formación del
cálculo diferencial.
Dominio, contradominio, tabulación y graficación
El dominio de una función f : A → B corresponde al conjunto formado por los posibles valores
para x y el contradominio o codominio corresponde a los posibles valores para y.
4.51
Elipse
¿Cuál es el dominio de la función f (x) =
a) x ∈ (5, ∞)
x −3
?
x −5
b) x ∈ (−∞, 5) ∪ (5, ∞)
d ) x ∈ (−∞, −5) ∪ (−5, ∞)
c) x ∈ R
e) x ∈ (−∞, −5) ∪ (5, ∞)
Solución .
La función es racional y el denominador debe ser distinto de cero, ya que la división entre
cero no está definida, por tanto el dominio es
D f = {x ∈ R|x ̸= 5}
o bien
x ∈ (−∞, 5) ∪ (5, ∞)
La respuesta correcta es el inciso b
4.52
Cálculo
¿Cuál es el dominio de la función f (x) =
a) x ∈ (5, ∞)
p
x − 5?
b) x ∈ (−∞, 5) ∪ [5, ∞)
d ) x ∈ [−5, ∞)
c) x ∈ [5, ∞)
e) x ≥ 0
Solución .
El radicando debe ser mayor o igual a cero, es decir x −5 ≥ 0, de donde x ≥ 5 por lo tanto,
el dominio es
D f = {x ∈ R|x ≥ 5}
o bien
x ∈ [5, ∞)
La respuesta correcta es el inciso c
4.53
Cálculo
¿Cuál es el dominio de la función f (x) = log (2x − 3)?
µ
¶
3
a) x ∈ , ∞
2
·
¶
3
b) x ∈ , ∞
c) x > 0
2
¶
µ
3
d)x ∈ R
e) x ∈ − , ∞
2
Solución .
Para determinar el dominio de esta función se debe tomar en cuenta que la función logaritmo solo está definida para números positivos, por lo tanto, se plantea la desigualdad y
se resuelve:
3
2x − 3 > 0 → 2x > 3 → x >
2
½
¾
3
D f = x ∈ R|x >
2
o bien
µ
¶
3
x ∈ ,∞
2
La respuesta correcta es el inciso a.
La gráfica de una función f es el conjunto de puntos del plano cartesiano donde las coordenadas son de la forma (x, y) donde y = f (x). El método general para gráficar cualquier función
es el de tabulación. Consiste en dar valores a la variable x y con ellos calcular los correspondientes a la variable y, los cuales se van anotando en una tabla. Después se localiza en el plano
cartesiano cada punto tabulado así y se unen para obtener la forma de la gráfica buscada.
4.54
Cálculo
Selecciona la ecuación que corresponda a la siguiente gráfica.
b) y = x 2 − 4x + 5
a) y = −4x + 5
d) y =
1
+1
x
c) y = x 3 + x 2 + x − 11
e) y = x + 2 + ln x
Solución .
La gráfica es una parábola vertical, su eje es paralelo al eje Y . La respuesta correcta es el
inciso b.
4.55
Cálculo
Selecciona la ecuación que corresponda a la siguiente gráfica.
a) y = x 2 + 15
d) y =
c) y = x 3 + x 2 + 11
b) y = cos x
1
x
e) y =
p
x +4−5
Solución .
La gráfica de la función tiene al eje "y" como asíntota vertical, esto ocurre cuando x = 0.
La respuesta correcta es el inciso d .
4.56
Cálculo
Selecciona la ecuación que corresponda a la siguiente gráfica.
a) y =
p
x +2
b) y = cos x
d) y =
1
x
c) y = x 3 + x 2 + 11
e) y = x − 5
Solución .
La gráfica de la función es la mitad superior de una parábola horizontal definida únicamente si x ≥ −2. La respuesta correcta es el inciso a.
4.9
Operaciones con funciones
Sean f y g dos funciones se definen las operaciones entre funciones se definen respectivamente como:
Suma ( f + g )(x) = f (x) + g (x)
Resta ( f − g )(x) = f (x) − g (x)
Multiplicación
µ ¶ ( f · g )(x) = f (x) · g (x)
f (x)
f
División
(x) =
g
g (x)
Composición de funciones ( f ◦ g )(x) = f (g (x))
4.57
Operaciones con funciones
Sean las funciones f (x) = x 2 − 7x + 10 y g (x) = x − 5
1) ¿Cuál es el resultado de la suma f (x) + g (x)?
a) x 2 + 6x + 5
b) y = x 2 − 6x − 5
d ) x2 + 5
e) x 2 − 6x
Solución .
f (x) + g (x) = (x 2 − 7x + 10) + (x − 5) = x 2 − 6x + 5
La respuesta correcta es el inciso c.
c) x 2 − 6x + 5
4.58
Operaciones con funciones
Sean las funciones f (x) = x 2 − 7x + 10 y g (x) = x − 5
2) ¿Cuál es el resultado de la resta f (x) − g (x)?
a) x 2 − 8x + 15
b) x 2 − 8x − 15
c) x 2 + 8x + 15
e) x 2 − x + 15
d)0
Solución .
f (x) − g (x) = (x 2 − 7x + 10) − (x − 5) = x 2 − 8x + 15
La respuesta correcta es el inciso a.
4.59
Operaciones con funciones
Sean las funciones f (x) = x 2 − 7x + 10 y g (x) = x − 5
3) ¿Cuál es el resultado de la multiplicación f (x) · g (x)?
a) x 3 − 12x 2 + 45x − 50
b) 12x 2 + 45x − 50
d ) x 4 − 12x 3 + 45x − 50
c) x 3 + 8x + 15
e) x 3 + 45x − 50
Solución .
f (x) · g (x) = (x 2 − 7x + 10) · (x − 5)
= x 3 − 7x 2 + 10x − 5x 2 + 35x − 50 = x 3 − 12x 2 + 45x − 50
La respuesta correcta es el inciso a.
4.60
Operaciones con funciones
Sean las funciones f (x) = x 2 − 7x + 10 y g (x) = x − 5
4) ¿Cuál es el resultado de la composición (g ◦ f )(x)?
a) x 2 + 7x + 5
b) x 2 + 5
d ) x 2 − 7 − 5x
c) x 3 − 7x + 5
e) x 2 − 7x + 5
Solución .
(g ◦ f )(x) = g ( f (x)) = g (x 2 − 7x + 10) = (x 2 − 7x + 10) − 5
= x 2 − 7x + 5
La respuesta correcta es el inciso e.
4.10
Límite de una función
Si al aproximar x lo suficientemente cerca de un número a (sin ser a) tanto del lado izquierdo como del derecho, f (x) se aproxima a un número L, entonces el límite cuando x tiende al
número a es L. Esto lo escribimos:
lı́m f (x) = L.
x→a
4.61
Límites
sin x
.
x→0 x
Calcula, usando el método numérico, el valor del siguiente límite lı́m
a) 0
b) − 1
c) − 2
d)1
e) 2
Solución .
Evaluamos a la función con valores muy cercanos a 0 por la izquierda y por la derecha.
Observe que la función no está definida en x = 0 y que los valores de la función se
aproximan al número 1.
x
−0.005
−0.004
−0.003
−0.001
f (x) = sin x
0.999995833
0.99999733
0.9999985
0.9999995833
x
0.005
0.004
0.003
0.001
f (x) = sin x
0.999995833
0.99999733
0.9999985
0.9999995833
sin x
= 1. La respuesta correcta es el inciso d .
x→0 x
Note que lı́m
4.62
Límites
x2 − 9
?
x→3 x − 3
¿Cuál es el valor del límite lı́m
a) 6
b) − 6
c) 0
d)1
e) 2
Solución .
Al sustituir x con 0 en la función el límite se indetermina
x 2 − 9 (3)2 − 9 0
=
=
x→3 x − 3
(3) − 3
0
lı́m
Para eliminar la indeterminación se factoriza el numerador por diferencia de cuadrados,
luego el límite es
(x − 3)(x + 3)
x2 − 9
= lı́m
= lı́m (x + 3) = 6.
x→3
x→3
x→3 x − 3
x −3
lı́m
La respuesta correcta es el inciso a.
4.11
Derivada de una función
Al considerar a la derivación como la operación básica, Newton produjo sencillos métodos
analíticos que unificaban muchas técnicas diferentes desarrolladas previamente para resolver
problemas, en apariencia no relacionados, como calcular áreas, tangentes, longitud de curvas
y los máximos y mínimos de funciones.
El valor de la derivada en cualquier punto de la curva es igual a la pendiente de la recta tangente en ese punto.
4.63
Derivadas
¿Cuál es la derivada de la función y = x 3 + 2x 2 − 4x + 5?
a) 3x 2 + 4x
b) 3x 2 + 4x − 4
d ) x 2 + 4x − 4
c) 3x 3 + 4x − 4
e) 3x 2 + x − 4
Solución .
Al aplicar las fórmulas respectivas se obtiene
dy
d 3
d 3
d
d
d
=
(x + 2x 2 − 4x + 5) =
(x ) +
(2x 2 ) −
(4x) +
(5)
dx dx
dx
dx
dx
dx
=
d 2
d
d 3
d
(x ) + 2
(x ) − 4
(x) +
(5) = 3x 2 + 2(2x) − 4(1)
dx
dx
dx
dx
= 3x 2 + 4x − 4.
La respuesta correcta es el inciso b.
4.64
Derivadas
x2 − 5
?
1 − 3x 2
−28x
b)
1 − 3x 2
¿Cuál es la derivada de la función f (x) =
a)
−28x
(1 − 3x 2 )2
d)
−28x
(1 − 3x 2 )4
e)
c)
28
(1 − 3x 2 )2
28x
(1 − 3x)2
Solución .
Al aplicar las fórmulas respectivas se obtiene
f ′ (x) =
(1 − 3x 2 )(x 2 − 5)′ − (x 2 − 5)(1 − 3x 2 )′ (1 − 3x 2 )(2x) − (x 2 − 5)(−6x)
=
(1 − 3x 2 )2
(1 − 3x 2 )2
=
2x − 6x 3 + 6x 3 − 30x
−28x
=
(1 − 3x 2 )2
(1 − 3x 2 )2
La respuesta correcta es el inciso a.
4.65
Derivadas
¿Cuál es la derivada de la función y = 4 cos(x 2 − 1)?
a) − 8x
b) sin(x 2 − 1)
c) − 8x · sin(x 2 − 1)
d ) − 8x · cos(x 2 − 1)
Solución .
Al aplicar la fórmula
e) cos(x 2 − 1)
d
dv
cos v = − sin v
se obtiene
dx
dx
·
¸
d
d
d 2
dy
2
2
2
=
4 cos(x − 1) = 4
cos(x − 1) = 4 − sin(x − 1)
(x − 1)
dx dx
dx
dx
= −4 sin(x 2 − 1) · 2x = −8x · sin(x 2 − 1)
La respuesta correcta es el inciso c.
4.12
Integral definida
Representa el área que forma la función f (x) con el eje x en el intervalo [a, b].
Cálculo de una integral definida:
a) Se integra la diferencial de la función.
b) Se sustituye la variable de la integral que se obtuvo, por los límites superior e inferior, y los
resultados se restan para obtener el valor de la integral definida.
4.66
Integral definida
Z6
¿Cuál es el el valor de la integral
2
dx
?
p
3x − 2
a) 6
b) − 6
c) 0
d)
1
3
e)
4
3
Solución .
Se integra y se sustituyen los límites
Z6
2
·
¸6 · p
¸
dx
2p
2
2p
=
3x − 2 =
3(6) − 2 −
3(2) − 2
p
3
3
3
3x − 2
2
·
¸
2
2
8 4 4
= (4) − (2) = − =
3
3
3 3 3
4.67
Integral definida
¿Cuál es el valor del área comprendida entre la curva y = 2x − x 2 y el eje x desde x = 0
hasta x = 2?
a) 6
b) − 6
c) 0
d)
1
3
e)
4
3
Solución .
Se calcula la integral definida
Z2
0
·
¸2 ·
¸ ·
¸
x3
(2)3
(0)3
(2x − x 2 )d x = x 2 −
= (2)2 −
− (0)2 −
3 0
3
3
4−
La respuesta correcta es el inciso e.
8 4
=
3 3
5
Física
Fundamentos teórico-prácticos
Sistemas de unidades y conversiones
Medición: Se llama así a la comparación de dos o más cantidades, para lo que se toma a
una de ellas como medida patrón.
Unidades fundamentales: Están formadas por unidades de longitud, masa, tiempo, estas
pueden ser:
Unidades fundamentales
Longitud
Masa
Tiempo
Temperatura
Ejemplos
Año, día, hora (hr), Minuto (min), Segundo (s) etc...
.....
..............
................
Unidades derivadas: Son las que resultan de combinar dos o más unidades fundamentales mediante operaciones matemáticas.
Sistema de unidades
Estos sistemas se forman con determinados tipos de unidades, que se emplean según el caso.
Ejemplos:
Física
5.1
126
Equivalencias
Relaciones entre las unidades fundamentales de los diferentes sistemas de unidades. Ejemplos:
Conversiones
Equivalencias que existen entre las unidades de medida. Para realizar conversiones es necesario auxiliarse de las equivalencias.
5.1
Conversiones
1.- El resultado de convertir 0.45 horas a segundos es:
a) 620 s
b) 1620 s
c) 1200 s
d ) 7200 s
e) 3600 s
Solución .
Equivalencia: 1 h = 3 600 s
³
0.45 h
1
´¡
3600 s
1h
La respuesta es el inciso b.
5.2
Conversiones
2.- Al convertir 587 mill a km se obtiene:
a) 1580.3 km
b) 1609 km
c) 1.58 km
¢
=
1620 hs
h
= 1620 s
d ) 944.5 km
e) 1580 km
Solución .
Equivalencia: 1 mill = 1 609 km, 1 km = 1 000 m
³
´¡
¢ ¡ 1000 m ¢
587 mi l l
1609 m
1
1 mi l l
1 km
= 944.5 km
La respuesta es el inciso d.
5.3
Conversiones
3.- Al convertir 95 km/h a m/s se obtiene:
a) 26.38 m/s
b) 120 m/s
c) 1.58 m/s
d ) 4.5 m/s
e) 15.8 m/s
Solución .
Equivalencia: 1 km = 1 000 m, 1 h = 3 600 s
³
´¡
¢³
95 km
1000 m
1h
1 km
1h
3600 s
´
= 26.38 m/s
La respuesta es el inciso a.
5.4
Conversiones
4.- Al convertir 60 millas/h a ft/s se obtiene:
a) 45.82 ft/s
b) 220 ft/s
c) 87.98 ft/s
d ) 48.39 ft/s
e) 19.84 ft/s
Solución .
Equivalencia: 1 milla = 1 609 m, 1 m = 3.281 ft y 1 h = 3 600 s
´¡
³
¢ ³ 3.281 f t ´ ³ 1 h ´
1609 m
60 mi l l
1h
1 mi l l
1m
3600 s = 87.98 f t /s
La respuesta es el inciso c.
Suma de vectores
Dados los vectores F⃗1 = (F 1x , F 1y ), F⃗2 = (F 2x , F 2y ) y F⃗3 = (F 3x , F 3y ), el vector resultante representa
la suma de ellos.
5.5
Suma de vectores
⃗=
1.- La magnitud del vector resultante al realizar la suma de los vectores ⃗
A = (6 N , 0) y B
(0, −8 N ) es:
a) 80 N
b) 45 N
c) 10 N
d ) 18 N
e) 36 N
Solución .
La respuesta es el inciso c
5.6
Suma de vectores
2.- La magnitud del vector resultante al realizar la suma de los vectores F⃗1 =
(−8 N , 12 N ) y F⃗2 = (4 N , −9 N ) es:
a) 12 N
b) 5 N
c) 3 N
d ) 17 N
e) 21 N
Solución .
La respuesta es el inciso b.
5.7
Suma de vectores
3.- En la siguiente figura, ¿cuál es la magnitud del vector resultante?
a) 12.7 N
b) 5.25 N
c) 31.2 N
d ) 10.5 N
e) 11.18 N
Solución .
El desarrollo es:
La respuesta es el inciso e.
5.2
Mecánica
Equilibrio estático
Para que un cuerpo se encuentre en equilibrio debe satisfacer las siguientes condiciones:
Que el cuerpo se encuentre en reposo respecto a un marco de referencia (plano cartesiano).
Que el cuerpo se encuentre en movimiento rectilíneo con velocidad constante (equilibrio traslacional).
Primera condición de equilibrio Un cuerpo se encuentra en equilibrio si la suma vectorial de
todas las fuerzas que actúan sobre él es igual a cero.
F⃗1 + F⃗2 + F⃗3 + ... = 0
P
F⃗x = 0 y
P
F⃗y = 0
Segunda condición de equilibrio (equilibrio rotacional) Para que un cuerpo se encuentre en
equilibrio rotacional, la suma de los momentos de torsión que actúan sobre él debe ser igual a
cero.
P
τ = 0 Donde τ = torque o momento
El torque o momento de torsión que produce una fuerza con respecto a un eje de giro, se define
como el producto de la magnitud de la fuerza por el brazo de palanca (distancia desde el punto
donde actúa la fuerza al eje de rotación).
Donde:
F = fuerza [N, dinas, lb]
d = brazo de palanca [m, cm, ft]
τ = torque [N·m, dinas·cm, lb·ft]
La balanza de brazos es una aplicación de la segunda condición de equilibrio.
Formula:
F1 · d1 = F2 · d2
Donde:
F 1 y F 2 = fuerzas aplicadas en los extremos de la balanza
d 1 y d 2 = brazos de palanca
5.8
Equilibrio estático
1. ¿Cuál es la magnitud de la tensión T en la cuerda para que el cuerpo se encuentre en
equilibrio?
a) 820 N
b) 500 N
c) 750 N
d ) 1200 N
e) 1800 N
Solución .
Al aplicar la primera condición de equilibrio se obtiene:
P
F⃗x = 0
P
F⃗y = 0 −→ T − 1200 N = 0
De la última igualdad se despeja el valor de T .
T − 1200 N = 0
T = 1200 N
La respuesta es el inciso d.
5.9
Equilibrio estático
2.- En la siguiente figura, las cuerdas A y B son del mismo material, si se aplica una fuerza
F sobre la cuerda B, ¿cuál de las siguientes afirmaciones es verdadera?
a) Se rompre primero la cuerda A.
b) Se rompre primero la cuerda B.
c) Ambas cuerdas se rompen juntas.
d ) Se equilibran las fuerzas en las cuerdas y no sucede nada.
e) El bloque se desplaza horizontalmente.
Solución .
Al aplicar la fuerza F sobre la cuerda B, en la cuerda A actúan dos fuerzas, la del peso w
del cuerpo y F , entonces la cuerda que se rompe primero es la cuerda A.
La respuesta es el inciso a.
5.10
Equilibrio estático
3.- La magnitud de la fuerza F que equilibra la balanza en el siguiente diagrama es:
a) 540 N
b) 150 N.
c) 480 N.
d ) 20 N.
e) 96 N.
Solución .
Aplicando la fórmula: F 1 · d 1 = F 2 · d 2
F (4 m) = (120 N )(5 m) F (4 m) = 600 N · m F =
600 N · m
4m
= 150 N
La respuesta es el inciso b.
Movimiento rectilíneo uniforme y uniformemente acelerado.
Movimiento rectilíneo uniforme Movimiento por el que los cuerpos se desplazan en una trayectoria recta con velocidad constante recorriendo distancias iguales en tiempos iguales.
Velocidad media
Se define como la razón entre el desplazamiento de un cuerpo y el intervalo de tiempo en que
sucede.
v=
d espl azami ent o
t i empo
En el movimiento rectilíneo uniforme la velocidad media se define como la razón entre la distancia total recorrida por el cuerpo y el tiempo total que tarda en recorrer dicha distancia.
v=
d i st anci a t ot al
t i empo t ot al
=
d 2 −d 1
t 2 −t 1
=
d 3 −d 2
t 3 −t 2
=
d 3 −d 1
t 3 −t 1
= ...
Gráfica de la distancia (d ) recorrida por un cuerpo en función del tiempo (t )
Donde:
d 1 = distancia inicial t 1 = tiempo inicial
d 2 = distancia final
t 2 = tiempo final
Si d 2 − d 1 = d y t 2 − t 1 = t , entonces:
v=
Donde: d = distancia total [m, km, ft]
t = tiempo total [s, h, s]
v= velocidad media [m/s, Km/h, ft/s]
d
t
5.11
Movimiento rectilíneo uniforme
1.- La siguiente gráfica muestra a un cuerpo que se mueve con velocidad constante,
¿Cuál es la velocidad del cuerpo?
a) 108 m/s
b) 18 m/s
c) 3 m/s
d ) 6 m/s
e) 96 m/s
Solución .
Se toman dos parejas de puntos y se aplica la fórmula:
Datos:
d 1 = 18 m
d 2 = 36 m
t1 = 6 s
t 2 = 12 s
Fórmula:
−d 1
v = dt22 −t
1
Sustitución y resultado:
m
18 m
m
v = 3612m−18
s−6 s = 6 s = 3 s
La respuesta es el inciso c.
5.12
Movimiento rectilíneo uniforme
2.- Un cuerpo recorre 300 km en 5 horas. ¿Cuál es su velocidad media en ese intervalo de
tiempo?
a) 150 km/h
b) 50 km/h
c) 1500 km/h
d ) 60 km/h
e) 6 km/h
Solución .
Datos: d = 300 km
t =5h
v =?
Fórmula:
v = dt
Sustitución y resultado:
v = 3005 hkm = 60 km
h
La respuesta es el inciso d.
5.13
Movimiento rectilíneo uniforme
3.- Una partícula viaja a razón de 9 m/s ¿Qué distancia recorre al cabo de 6 minutos?
a) 54 m
b) 540 m
c) 5400 m
d ) 3240 m
e) 6480 m
Solución .
Se despeja la distancia de la fórmula de la velocidad media y se sustituyen los datos.
Datos:
d =?
t = 6 min = 6(60 s)=360 s
v = 9 m/s
Fórmula:
v = dt −→ d = v · t
Sustitución y resultado:
d = (9 m/s)(360 s) = 3240 m
La respuesta es el inciso d.
Movimiento rectilíneo uniformemente acelerado
En este movimiento los cuerpos se desplazan en una trayectoria rectilínea con aceleración
constante.
Aceleración
Cambio en la velocidad de un cuerpo con respecto al tiempo.
a=
v f −v i
t f −t i
a=
v f −v i
t
Si t f − t i = t la fórmula se expresa como:
Donde:
v i = velocidad inicial [ ms , km
h ,
v i = velocidad final [ ms , km
h ,
ft
s ]
ft
s ]
t = intervalo de tiempo [s, h]
a = aceleración [ m
, km ,
s2 h2
ft
]
s2
Fórmulas para el movimiento rectilineo uniformemente acelerado:
Caída libre
En este movimiento los cuerpos describen una trayectoria rectilínea de arriba hacia abajo con
aceleración constante e igual a la gravedad.
a = g = 9.81 m/s 2
Todos los cuerpos en caída libre son acelerados hacia el centro de la Tierra y su velocidad aumenta de manera uniforme con respecto al tiempo. Si dos cuerpos de masas distintas se dejan
caer de una determinada altura, ambos llegan al mismo tiempo al suelo y con la misma velocidad, esto sin considerar la fricción con el aire.
Fórmulas para el movimiento rectilineo uniformemente acelerado (caída libre):
Donde:
t =tiempo [s]
h =altura [m]
v =velocidad [m/s]
g = aceleración de la gravedad = 9.81 m/s 2
5.14
Movimiento rectilíneo
1.- Un automóvil se mueve a razón de 20 m/s, después de 5 segundos se mueve a razón
de 30 m/s ¿Cuál es su aceleración?
a) 10 m/s 2
b) 30 m/s 2
c) 2 m/s 2
d ) 1 m/s 2
e) 20 m/s 2
Solución .
Datos:
v i = 20 ms
v f = 30 ms
t =5 s
a =?
Fórmula:
v f −v i
a= t
Sustitución y resultado:
m/s
2
a = 30 m/s−20
= 105m/s
5s
s = 2 m/s
La respuesta es el inciso c.
5.15
Movimiento rectilíneo
2.- Un cuerpo parte del reposo y se acelera a razón de 4 m/s 2 , ¿Qué distancia recorre
después de 5 segundos?
a) 10 m
b) 20 m
c) 200 m
d ) 50 m
e) 100 m
Solución .
Datos:
vi = 0
a = 4 m/s 2
t =5 s
d =?
Fórmula:
2
d = v i · t + a·t2
Sustitución y resultado:
2
2
d = (0)(5 s) + (4 m/s2 )(5 s) = 0 + 1002 m = 50 m
La respuesta es el inciso d.
5.16
Movimiento rectilíneo
3.- Se deja caer un cuerpo desde la parte más alta de un edificio y tarda 3 segundos en
llegar al suelo. La altura del edificio es:
a) 10.38 m
b) 67.82 m
c) 9.81 m
d ) 28.50 m
e) 44.15 m
Solución .
Datos:
h=?
g = 9.81 m/s 2
t =3 s
Fórmula:
g ·t 2
h= 2
Sustitución y resultado:
2
2
)(3 s)2
)(9 s 2 )
h = (9.81 m/s
= (9.81 m/s
= 44.15 m
2
2
La respuesta es el inciso e.
Movimiento circular uniforme.
Las expresiones matemáticas del movimiento circular se enuncian generalmente con magnitudes angulares como el desplazamiento angular, la velocidad angular y la aceleración angular.
En el movimiento circular de una partícula, resulta práctico considerar que el origen del sistema de referencia se encuentra en el centro de su trayectoria circular.
El desplazamiento angular es la magnitud física que cuantifica la magnitud de la rotación que
experimenta un objeto de acuerdo con su ángulo de giro, se representa con la letra griega θ
(theta) y sus unidades de medida son: el radián, cuando el sistema usado es el Internacional.
La magnitud de la velocidad angular representa el cociente entre la magnitud del desplazamiento angular de un cuerpo y el tiempo que tarda en efectuarlo:
ω=
θ
t
Donde:
ω = magnitud de la velocidad angular [r ad /s]
θ = magnitud del desplazamiento angular [r ad ]
t = tiempo en que efectúa el desplazamiento [s]
La magnitud de la velocidad angular se puede expresar en función de los cambios en la magnitud de su desplazamiento angular con respecto al cambio en el tiempo de lasiguiente manera:
ω=
∆θ
∆t
=
θ2 −θ1
t 2 −t 1
La magnitud de la velocidad angular también se puede determinar si se conoce su periodo (T ),
es decir, el tiempo que tarda en dar una vuelta completa o una revolución (360°= 2pi radianes).
La expresión que se utiliza es:
ω=
2π r ad
T
=
2 r ad
T s
Como T = 1/ f , la magnitud de la velocidad angular también se puede determinar por:
ω = 2π f
Donde:
f = frecuencia (es el número de vueltas, revoluciones o ciclos que efectúa un móvil en un segundo) [número de ciclos/ s]
5.17
Movimiento circular
1.- ¿Cuál es la magnitud de la velocidad angular de una llanta de camión que gira
desplazándose 12 rad en 0.5 segundos?
a) 6 rad/s
b) 30 rad/s
c) 24 rad/s
d ) 150 rad/s
e) 2 rad/s
Solución .
Datos:
ω =?
θ = 12 rad
t = 0.5 s
Fórmula:
ω = θt
Sustitución y resultado:
ad
ω = 12r
0.5 s = 24 r ad /s
La respuesta es el inciso c.
5.18
Movimiento circular
2.- Determinar la magnitud de la velocidad angular y la frecuencia de una pelota atada a
un hilo si gira con un periodo de 0.6 s.
a) 6 rad/s y 2.5 ciclos/s
b) 10.47 rad/s y 1.67 ciclos/s
c) 5.62 rad/s y 1.8 ciclos/s
d ) 0.62 rad/s y 2.48 ciclos/s
e) 12.6 rad/s y 3.8 ciclos/s
Solución .
Datos:
ω =?
f =?
T = 0.6 s
Fórmulas:
ω = 2π
T
f = T1
Sustitución y resultado:
ω = 2(3.14)
0.6 s = 10.47 r ad /s
f = 0.61 s = 1.67 ciclos/s
La respuesta es el inciso b.
5.19
Movimiento circular
3.- Encontrar la magnitud de la velocidad angular de una rueda de esmeril que gira a
810 rpm, así como la magnitud de su desplazamiento angular, si su movimiento duró 2
minutos.
a) 45.62 rad/s y 1213.5 rad
b) 92.5 rad/s y 3500.6 rad
c) 62.45 rad/s y 12 173.8 rad
d ) 85.36 rad/s y 22 245.6 rad
e) 84.78 rad/s y 10 173.6 rad
Solución .
Datos:
ω =?
θ =?
f =810 rpm
t = 2 min=120 s
Fórmulas:
ω = 2π f
θ=ω t
Sustitución y resultado:
Primero es necesario convertir la frecuencia de rpm a ciclos/s
r ev
1 mi n
810 mi
n · 60 s = 13.5 r ev/s = 13.5 ci cl os/s
ω = 2(3.14)(13.5) = 84.78 r ad /s
θ = (84.78 r ad /s)(120 s) = 10 173.6 r ad
La respuesta es el inciso e.
Leyes de Newton: aplicaciones.
Primera ley de Newton (ley de la inercia)
Todo cuerpo en movimiento o reposo conserva ese estado, a menos que una fuerza externa lo
modifique. Esta ley indica que en ausencia de fuerzas, los cuerpos en reposo continuarán en
reposo y los cuerpos en movimiento se moverán en una línea recta con velocidad constante.
Fuerza
La fuerza es una magnitud de carácter vectorial. Sus unidades son los Newtons (N), dinas, libras (lb), etcétera.
Segunda ley de Newton (ley de la masa inercial)
La aceleración que un cuerpo experimenta es directamente proporcional a la resultante de todas las fuerzas que actúan sobre él e inversamente proporcional a su masa. La dirección y el
sentido en que se mueve el cuerpo es la misma que la de la fuerza resultante.
⃗
a=
⃗
F
m
en magnitud a =
F
m
o bien F = m · a
Donde:
a = aceleración [m/s 2 , cm/s 2 , f t /s 2 ]
F = fuerza [N, dinas, lb]
m = masa [kg, g, slugs]
Concepto de masa
Es la medida de la inercia de un cuerpo. Las unidades de masa son los kilogramos (kg), gramos
(g), slugs, etcétera.
Concepto de peso (w)
Es la fuerza ejercida por la tierra sobre los cuerpos.
w=m· g
Donde:
m = masa [kg, g, slugs]
ft
g = gravedad [9.81 m
, 981 cm
, 32 s 2 ]
s2
s2
w = peso [N, dinas, lb]
Tercera ley de Newton (ley de la acción y la reacción)
A toda fuerza de acción corresponde una de reacción de igual magnitud, pero con sentido
opuesto.
Ley de gravitación universal
La fuerza de atracción que experimentan dos cuerpos es directamente proporcional al producto de sus masas e inversamente proporcional al cuadrado de la distancia que los separa.
5.20
Movimiento circular
1.- Sobre una caja de 40 kg actúa una fuerza de 500 N. ¿Qué aceleración le proporciona
la fuerza a la caja?
a) 20 000 m/s 2
b) 3000 m/s 2
c) 12.5 m/s 2
d ) 0.08 m/s 2
e) 540 m/s 2
Solución .
Datos:
m = 40 kg
F = 500 N
a =?
Fórmula:
F
a=m
Sustitución y resultado:
N
2
a = 500
40 kg = 12.5 m/s
La respuesta es el inciso c.
5.21
Movimiento circular
2.- Una masa de 25 kg es acelerada a razón de 10 m/s 2 . Calcula la magnitud de la fuerza
que la acelera.
a) 250 N
b) 300 N
c) 125 N
d ) 80 N
e) 40 N
Solución .
Datos:
m = 25 kg
a = 10 m/s 2
F =?
Fórmula:
F =m · a
Sustitución y resultado:
F = (25 kg )(10 m/s 2 ) = 250 N
La respuesta es el inciso a.
5.22
Movimiento circular
3.- ¿Cuál es el peso de una persona de 70 kg de masa?
a) 315 N
b) 2240 N
c) 7.14 N
d ) 686.7 N
e) 548.27 N
Solución .
Datos:
m = 70 kg
g = 9.81 m/s 2
w =?
Fórmula:
w =m · g
Sustitución y resultado:
w = (70 kg )(9.81 m/s 2 ) = 686.7 N
La respuesta es el inciso d.
Trabajo, potencia y energía mecánica.
El trabajo es una magnitud escalar, que es igual al producto de la componente de la fuerza, que
actúa en la misma dirección en que se efectúa el movimiento del cuerpo, por la distancia que
se desplaza el cuerpo. Si una persona empuja un mueble por una superficie, entonces realiza
un trabajo mecánico.
T =F · d
Donde:
F = fuerza [N, dinas, lb]
d = desplazamiento [m, cm, ft]
T = trabajo [Joules (J), ergios, l b · f t ]
1 joule = 1 N · m = 1 kg
m2
s2
y 1 ergio = 1 dina · cm = 1 g
cm 2
s2
La energía es la capacidad que tiene cualquier cuerpo para desarrollar un trabajo. Las unidades
de la energía en el sistema internacional son los joules (J). Existen 2 tipos de energía mecánica,
la cinética y la potencial.
Energía cinética
Es aquella que tiene cualquier cuerpo en movimiento.
E c = 12 m · v 2
Donde
m = masa [kg, g, slug]
v = velocidad [m/s, cm/s, ft/s]
E c = energía cinética [Joules (J), ergios, l b · f t ]
Energía potencial
Es aquella que tiene todo cuerpo en virtud de su posición.
Ep = m · g · h
o
Ep = w · h
Donde
m = masa [kg, g, slug]
h = altura [m, cm, ft]
E p = energía potencial [Joules (J), ergios, l b · f t ]
ft
g = gravedad [9.81 m
, 981 cm
, 32 s 2 ]
s2
s2
w = peso [N, dinas, lb]
Conservación de la energía mecánica
Si sobre un cuerpo en movimiento sólo actúan fuerzas conservativas, la suma de su energía
cinética y su energía potencial permanece constante y se llama: conservación de la energía
mecánica.
E = Ec + E p
Donde
E c = energía potencial
E p = energía potencial
E = energía mecánica
En un sistema de fuerzas conservativas, la energía cinética de un cuerpo se puede transformar
en energía potencial y viceversa, el cambio en la energía mecánica es cero, es decir, la energía
mecánica inicial es igual a la energía mecánica final.
Concepto de potencia
Rapidez con que se realiza un trabajo mecánico. La magnitud de la potencia es la razón del
trabajo mecánico realizado en la unidad de tiempo, sus fórmulas son:
P=
T
t
P=
F ·d
t
P =F ·v
Donde:
T = trabajo [Joules (J), ergios, l b · f t ]
t = tiempo [s]
F = fuerza [N, dinas, lb]
v = velocidad [m/s, cm/s, ft/s]
d = distancia [m, cm, ft]
P = potencia [watts, ergios/s, hp]
1 watt = 1 J · s; 1 hp=1
5.23
l b· f t
s ; 1 hp = 764 watts; 1 kw = 1 000 watts
Potencia
1.- Una fuerza levanta un cuerpo de 2400 N desde el suelo hasta una altura de 1.5 m.
¿Qué trabajo realiza la fuerza?
a) 360 x 102 J
b) 3.6 x 103 J
c) 36 x 106 J
d ) 7.8 x 103 J
e) 36 x 103 J
Solución .
Datos:
F = 2400 N
d = 1.5 m
T =?
Fórmula:
T = F · d = w ·d
Sustitución y resultado:
T = (2400 N )(1.5 m)
T = 3600 N · m
T = 3600 J = 3.6 x 103 J
La respuesta es el inciso b.
5.24
Potencia
2.- Determina la velocidad que lleva un cuerpo cuya masa es de 6 kg y tiene una energía
cinética de 675 J
a) 30 m/s
b) 225 m/s
c) 62 m/s
d ) 45 m/s
e) 15 m/s
Solución .
Datos:
m = 6 kg
E c = 675 J
v =?
Fórmula:
E c = 12 m · v 2
Despejando: v =
q
2E c
m
Sustitución
y resultado:
q
q
2(675 J )
1350 J
=
v=
6 kg
6 kg
q
m2
m
v = 225 s 2 = 15 s
La respuesta es el inciso e.
5.25
Potencia
3.- Una máquina realiza un trabajo de 90 000 J en 6 minutos. ¿Qué potencia desarrolla?
a) 850 watts
b) 250 watts
c) 4500 watts
d ) 200 watts
e) 500 watts
Solución .
Datos:
T = 90 000 J
t = 6 mi n = 6(60 s) = 360 s
P =?
Fórmula:
P = Tt
Sustitución y resultado:
000 J
P = 90360
s
P = 250 watts
La respuesta es el inciso b.
Presión hidrostática, principio de Arquímedes, principio de Pascal
Presión
Se define a la presión como la razón de la fuerza aplicada por unidad de área o superficie.
P=
F
A
Donde:
P = presión [ mN2 , Pascal=Pa]
F = fuerza [N]
A = área [m 2 ]
La fórmula indica que la presión es directamente proporcional a la fuerza e inversamente proporcional a la superficie. Si se disminuye el área sobre la que actúa una fuerza constante, la
presión aumenta; si el área sobre la que actúa la fuerza constante aumenta la presión disminuye.
Presión atmosférica
Es la presión que la atmósfera ejerce en todas direcciones sobre los cuerpos sumergidos en ella.
La presión atmosférica varía con la altura, a medida que ésta aumenta, la presión disminuye y
a nivel del mar tiene su máximo valor, que es igual a:
1 atm = 760 mm de Hg = 1.013 x 105
N
m2
Presión hidrostática
La presión que ejerce una columna de fluido en el fondo del recipiente que lo contiene es igual
a:
Ph = Pe · h o Ph = ρ · g · h
Donde:
P e = peso especifico [ mN3 ,
kg
gr
Di nas
]
cm 3
ρ = densidad [ m 3 , cm 3 ]
h = profundidad [m, cm]
ft
, 981 cm
, 32 s 2 ]
g = gravedad [9.81 m
s2
s2
P h = presión hidrostática [Pa, dinas/ cm 2 ]
Principio de Pascal
La presión ejercida sobre un fluido encerrado en un recipiente, se transmite con la misma intensidad a todos los puntos de las paredes del recipiente.
Prensa hidráulica
Para su funcionamiento este dispositivo aplica el principio de Pascal, la forman dos recipientes cilíndricos comunicados que contienen un fluido, la sección transversal de uno de ellos es
f
mayor que la del otro, cada recipiente tiene un émbolo, si se ejerce una presión P 1 = a en el
émbolo más pequeño, se obtiene una presión P 2 = FA en el émbolo mayor, de tal forma que
P 1 = P 2 , por tanto:
f
a
=
F
A
Donde:
f = fuerza aplicada en el émbolo menor [N, Dinas]
F = fuerza aplicada en el émbolo mayor [N, Dinas]
a = área del émbolo menor [m 2 , cm 2 ]
A = área del émbolo mayor [m 2 , cm 2 ]
Principio de Arquímedes
Cualquier cuerpo sumergido total o parcialmente en un fluido, experimenta un empuje o fuerza de flotación igual al peso del volumen desalojado del fluido.
E = Pe · V
o
E = ρ · g ·V
Donde:
nas
P e = Peso específico del fluido [ mN3 , Dicm
3 ]
3
3
V = Volumen desalojado [m , cm ]
g = Gravedad [9.81 m
, 981 cm
]
s2
s2
kg
gr
ρ = Densidad [ m 3 , cm 3 ]
E = Empuje [N , Di nas]
5.26
Presión
1.- Sobre una superficie de 0.0025 m 2 se ejerce una presión de 4000 Pa, ¿cuál es la
magnitud de la fuerza que origina esta presión?
a) 1000 N
b) 160 N
c) 10 N
d ) 1600 N
e) 4000 N
Solución .
Datos:
P = 4000 Pa
A = 0.0025 m 2
F =?
Fórmula:
P = FA −→ F = P · A
Sustitución y resultado:
F = (4000 P a)(0.0025 m 2 )
F = 10 N
La respuesta es el inciso c.
5.27
Presión
2.- ¿Cuál es la presión hidrostática que ejerce una columna de agua de 5 m de altura?
kg
(Considerarρ ag ua = 1000 m 3 y g = 9.81 m
)
s2
a) 4 000 Pa
b) 9 810 Pa
c) 1 000 Pa
d ) 9 550 Pa
e) 49 050 Pa
Solución .
Datos:
h=5m
kg
ρ ag ua = 1000 m 3
g = 9.81 m
s2
P h =?
Fórmula:
Ph = ρ · g · h
Sustitución y resultado:
kg
P h = (1 000 m 3 )(9.81 m
)(5 m)
s2
P h = 49 050 mN2
P h = 49 050 Pa
La respuesta es el inciso e.
5.28
Presión
3.- ¿Cuál es la fuerza que se debe aplicar en el émbolo menor de una prensa hidráulica de
0.016 m 2 de superficie, para que pueda levantar una caja de 12 000 N de peso colocada
en el émbolo mayor de 2.56 m 2 ?
a) 92 000 N
b) 75 N
c) 1 000 N
d ) 12 000 N
e) 24 000 N
Solución .
Datos:
a = 0.016 m 2
f =?
A = 2.56 m 2
F = 12 000 N
Fórmula:
f
F
a·F
a = A −→ f = A
Sustitución y resultado:
2
)(12 000 N )
N ·m 2
f = (0.016 m
= 192
2.56 m 2
2.56 m 2
f = 75 N
La respuesta es el inciso b.
5.3
Termometría
Temperatura: La temperatura de una sustancia es la suma de las energías cinéticas promedio
de sus moléculas. Para medir la temperatura de un cuerpo se emplean los termómetros, el más
común es el de mercurio. Este aparato puede estar graduado en escala Celsius, Fahrenheit o
Kelvin.
Escalas termométricas absolutas
Se define al cero absoluto como la temperatura en la cual la energía cinética de las moléculas
del agua es cero.
1 Para convertir grados Celsius a grados Kelvin se emplea la fórmula:
Tk = TC + 273
2 Para convertir grados Kelvin a grados Celsius se emplea la fórmula:
TC = TK − 273.
3 Para convertir grados Celsius a grados Fahrenheit se emplea la fórmula:
TF = 59 TC + 32 ó TF = 1.8TC + 32.
4 Para convertir grados Fahrenheit a grados Celsius se emplea la fórmula:
TC = 59 (TF − 32) ó TC =
5.3.1
Ejemplos
TF −32
1.8
5.29
Conversión
1. Al convertir 71.6 °F a grados Celsius se obtiene:
a) 57.5°C
b) 160.88°C
c) 22°C
d) 128.88°C
Solución .
Como TF =71.6°F
TC =
5.30
TF − 32 71.6 − 32 39.6
=
=
= 22◦C
1.8
1.8
1.8
Conversión
2. Al convertir 50°C a grados Kelvin se obtiene:
a) 323°K
b) 223°K
c) 122°K
d) 100°K
Solución .
TC = 50◦
TK =?
TK = TC + 273 = 50 + 273 = 323◦ K
5.31
Conversión
3. Al convertir 30°C a grados Fahrenheit se obtiene:
a) 12.2°F
b) 22°F
c)34.4°F
d) 86°F
Solución .
TC = 30◦C
TF =?
TF = 1.8TC + 32 = 1.8(30) + 32 = 54 + 32 = 86◦ F
5.4
Calor
El calor es una forma de energía que se transfiere de un cuerpo de mayor temperatura a otro de menor temperatura, también se define como la suma de las energías cinéticas de todas las moléculas
de un cuerpo. La unidad fundamental del calor en el sistema internacional es la caloría.
1 Caloría (cal): Cantidad de calor necesario para elevar en un grado Celsius la temperatura de
un gramo de agua (de 14.5°C a 15.5°C). El equivalente del calor en joules es 1 cal = 4.2J.
Otra equivalencia que se utiliza con frecuencia es 1 kcal=1 000 cal.
2 Capacidad calorífica: Se define como la razón que existe entre la cantidad de calor que recibe
un cuerpo y su incremento de temperatura.
3 Calor específico: Es la razón que existe entre la capacidad calorífica de una sustancia y su
masa. También es la cantidad de calor empleado para elevar en 1°C la temperatura de un
gramo de una sustancia.
Ce =
c
m
o Ce =
Q
m∗△T
Donde:
Q= Cantidad de calor (cal)
m=masa (g)
△T = incremento de temperatura (◦C )
C e = calor especifico( gc∗al◦C )
5.32
En los recipientes mostrados se encuentra contenido un mismo líquido, ¿Cuál de las siguientes afirmaciones es verdadera?
a) La temperatura del líquido contenido en el recipiente 1 aumenta más rápido que el
contenido en el 2.
b) La temperatura del líquido contenido en el recipiente 2 aumenta más rápido que el
contenido en el 1.
c) La temperatura aumenta al mismo ritmo en ambos recipientes.
d) La temperatura es la misma en ambos recipientes.
Solución .
Aunque el líquido es el mismo en ambos recipientes y es igual su calor específico, la
temperatura se incrementa más rápido en el recipiente 2 por tener una cantidad menor
de líquido que el recipiente 1, por tanto, la opción correcta es el inciso b.
5.5
Transferencia de calor
El calor se transfiere o conduce en tres formas diferentes:
a) Conducción: El calor se conduce o propaga en los sólidos debido al choque de las moléculas del cuerpo, sin que éste modifique su forma. Ejemplo: Cuando uno de los extremos
de una varilla metálica se pone en contacto con el fuego, después de un cierto tiempo el
otro extremo también se calienta. Esto se debe a que las moléculas del extremo expuesto al fuego vibran con mayor energía, parte de esa energía se transfiere a las moléculas
cercanas, las cuales a su vez transfieren ese exceso de energía a las otras moléculas. Así la
temperatura del cuerpo aumenta de manera uniforme y se distribuye en todo el cuerpo.
b) Convección: El calor se propaga a través de un fluido. Ejemplo: Al calentar agua en un recipiente, después de cierto tiempo se produce un movimiento en el líquido. Esto se debe
a que al recibir calor el agua del fondo del recipiente aumenta su temperatura y volumen,en consecuencia disminuye su densidad y este líquido tiende a ser reemplazado
por agua a menor temperatura (más fría) y de mayor densidad. Al proceso de circulación
de masas de agua caliente hacia arriba y fría hacia abajo, se le conoce como: corrientes
de convección.
c) Radiación: El calor se transfiere a través de ondas electromagnéticas. Ejemplo: Una situación cotidiana de la transferencia de calor por radiación es el calor que nos llega del Sol,
también conocida como rayos infrarrojos.
5.6
Termodinámica
La termodinámica se puede definir como la ciencia de la energía. Aunque todo el mundo tiene
idea de lo que es la energía, es difícil definirla de forma precisa. La energía se puede considerar
como la capacidad para causar cambios. El término termodinámica proviene de las palabras
griegas therme (calor) y dynamis (fuerza), lo cual corresponde a lo más descriptivo de los primeros esfuerzos por convertir el calor en energía. En la actualidad, el concepto se interpreta de
manera amplia para incluir los aspectos de energía y sus transformaciones, incluida la generación de potencia, la refrigeración y las relaciones entre las propiedades de la materia.
Leyes de la termodinámica: La termodinámica es la rama de la física que estudia la transformación del calor en trabajo y viceversa.
Ley cero de la termodinámica: (equilibrio térmico) Se dice que un sistema de cuerpos se encuentra en equilibrio térmico cuando el intercambio neto de energía entre sus elementos es
cero, la consecuencia es que los cuerpos se encuentren a la misma temperatura.
Primera ley: El calor que se suministra a un sistema es igual a la suma del incremento en la
energía interna de éste y el trabajo realizado por el sistema sobre sus alrededores, esto significa
o reafirma que la energía no se crea ni se destruye, sólo se transforma.
Segunda ley: Es imposible construir una máquina térmica que transforme en su totalidad el
calor en energía y viceversa. La eficiencia de una máquina térmica es la relación entre el trabajo mecánico producido y el calor suministrado.
5.33
Considere un automóvil de 1,200 kg a una velocidad constante de 90 km/h sobre una
carretera plana que después empieza a subir por una cuesta de 30º con respecto a la
horizontal. Si la velocidad del automóvil debe permanecer constante durante la subida,
determine la potencia adicional que debe suministrar el motor.
a) 147 kW
b) 155 kW
c) 142 kW
d) 197 kW
Solución .
Un automóvil que subirá por una cuesta debe mantener una velocidad constante
(energía cinética es cero). Se determinará la potencia adicional requerida. La potencia
adicional es el trabajo requerido por unidad de tiempo para que el automóvil logre
ascender, lo cual es igual al cambio de energía potencial del automóvil por unidad de
tiempo:
˙
Wg = mg △z
△t = mg V ver t i cal
Sustituyendo los datos conocidos, tenemos que:
)(25 ms ) · sen(30◦ )
Wg = (1200kg )(9.81 m
s2
Wg = 147kW
5.34
Determine la potencia requerida para acelerar un auto de 900 kg desde el reposo hasta
una velocidad de 80 km/h en 20 s sobre una carretera plana.
a) 222 kW
b) 11.1 kW
c) 111 kW
d) 14.9 hp
Solución .
Se determinará la potencia requerida para acelerar un automóvil hasta una velocidad especificada. Análisis: El trabajo necesario para acelerar un cuerpo es el cambio de energía
cinética de éste.
h¡
i
¢2
Wa = 12 m(V22 − V12 = 21 (900kg ) 22.22 ms − 02
Wa = 222k J
222k J
a
La potencia media se determina a partir de: Ẇa = W
△t = 20s = 11.1kW
5.7
Electricidad
Carga eléctrica: Es una propiedad que tienen los electrones, protones y neutrones. Los neutrones son partículas eléctricamente neutras, los electrones poseen una carga eléctrica negativa y
la carga de los protones es positiva. La unidad fundamental de carga en el sistema internacional es el coulomb [C].
Carga del electrón [e − ] = −1.6x10−19C
Carga del protón [e + ] = 1.6x10−19C
Las cargas eléctricas de signos iguales se repelen y las cargas eléctricas de signos opuestos se
atraen. Para detectar la presencia y naturaleza de las cargas eléctricas se emplea un aparato
llamado electroscopio.
Ley de Coulomb: La magnitud de la fuerza de atracción o repulsión que experimentan 2 cargas
eléctricas, es directamente proporcional al producto de las cargas e inversamente proporcional
al cuadrado de la distancia que las separa. Cuando las cargas eléctricas son del mismo signo, la
fuerza es repulsiva, y cuando son de signos opuestos la fuerza es atractiva.
F =K ·
q 1 ·q 2
d2
Donde: q 1 o q 2 =carga electrica (C)
d=distancia (m)
F=fuerza (N)
2
K= Constante de Coulomb =9x109 · ( NC·m2 )
5.35
1. El electrón y el protón de un átomo de hidrógeno están separados (en promedio) por
una distancia de aproximadamente 5.3x1011 m. Encuentre las magnitudes de la fuerza
eléctrica y la fuerza gravitacional entre las dos partículas.
a) 5.3x10− 11 N
b)3.6x10− 47 N
Solución .
F =Kd
q 1 ·q 2
d2
F = 8.99x109 (
c)3.6x10− 45 N
d) 3.8x10− 47 N
N · m 2 (−1.6x10−19C )(1.6x10−19C )
)
C2
(5.3x1011 m)2
F e = 8.2x10−8 N
5.36
Dos cargas puntuales q 1 = 25nC y q 2 = −75nC , y están separadas por una distancia de
3.0 cm. Calcule la magnitud y la dirección de a) la fuerza eléctrica que q1 ejerce sobre q2.
a) 0.019 N
b)0.0019 N
c)3.7x10− 3 N
d) −3.8x10− 3 N
Solución .
F =K
F 1 2 = 8.99x109 (
q1 · q2
d2
N · m 2 (25x10−9C )(−75x10−9C )
)
C2
(0.030m)2
F = 0.019N
Corriente eléctrica: Es la razón entre la cantidad de carga que atraviesa la sección transversal
de un conductor y el tiempo. La unidad de la corriente eléctrica en el sistema internacional es
el ampere (A). Resistencia Es la oposición que un conductor ofrece al flujo de la corriente eléctrica a través de él. La unidad de la resistencia en el sistema internacional es el ohm (Ω).
Ley de Ohm: La intensidad de corriente eléctrica que circula por un conductor es directamente
proporcional al voltaje aplicado en sus extremos e inversamente proporcional a su resistencia.
I = VR o V = I xR
Donde:
I = intensidad de corriente eléctrica [ampere=A]
V = diferencia de potencial o voltaje [volts= V]
R = resistencia del conductor [ohms =Ω]
5.37
Calcula la intensidad de la corriente que alimenta a una lavadora de juguete que tiene
una resistencia de 10 ohms y funciona con una batería con una diferencia de potencial
de 30 V.
a) 3 A
b) −3 A
c) 1.5 A
d) 3.8 A
Solución .
I=
V
o V = I ·R
R
Donde: R=10Ω y V=30V
30V
10Ω
I = 3A
I=
5.38
Calcula el voltaje, entre dos puntos del circuito de una plancha, por el que atraviesa una
corriente de 4 A y presenta una resistencia de 10 Ω.
a) 10 V
b) 30 V
c) 40 V
d) 35 V
Solución .
I=
V
o V = I ·R
R
Donde: R=10Ω e I=4A
V = 4A · 10Ω
V = 40V
5.8
5.8.1
Circuitos eléctricos
Circuitos en serie.
Todos los circuitos conectados en serie presentan las siguientes características:
La intensidad de corriente en cada resistencia es la misma.
I T = I 1 = I 2 = I 3 = ...
La resistencia total del circuito es igual a la suma de todas las resistencias.
R T = R 1 + R 2 + R 3 + ...
La diferencia de potencial total es igual a la suma de las diferencias de potenciales de cada resistencia.
VT = V1 + V2 + V3 + ...
5.39
Las resistencias de 5Ω, 10Ω y 20Ω se conectan en serie. ¿Cuál es la resistencia total del
circuito?
a) 5Ω
b) 15 Ω
c) 35 Ω
d) 10 Ω
Solución .
Datos: Las resistencias de 5Ω, 10Ω y 20Ω
R T = R 1 + R 2 + R 3 + ...
R T = 5Ω + 10Ω + 20Ω
R T = 35Ω
5.40
Las resistencias de 3ω, 4 ω y 5 ω se conectan en serie a una batería de 120 volts. ¿Cuál es
la intensidad de corriente que circula por el circuito? a) 40 A
b) 30 A
c) 10 A
d)
24 A
Solución .
Datos: Las resistencias de 3Ω, 3Ω y 5Ω
R T = R 1 + R 2 + R 3 + ...
R T = 3Ω + 4Ω + 5Ω
R T = 12Ω
120V
Ademas: I = VR I = V 12Ω
I = 10A
5.8.2
Circuitos de resistencias en paralelo
Todos los circuitos conectados en paralelo presentan las siguientes características:
La intensidad de corriente total es igual a la suma de todas las intensidades en cada resistencia.
I T = I 1 + I 2 + I 3 = ...
La resistencia total del circuito se obtiene con la fórmula:
1
RT
=
1
R1
+ R12 + R13 + ..
La diferencia de potencial total es igual a la diferencia de potencial de cada resistencia.
VT = V1 = V2 = V3 = ...
5.41
Una resistencia de 6 Ω se conecta en paralelo con otra de 3 Ω. ¿Cuál es la resistencia total
o equivalente del circuito?
a) 3 Ω
b) 9 Ω
c) 2 Ω
d) 1 Ω
Solución .
Datos: R 1 = 6Ω R 2 =3 Ω
1
RT
=
1
R1
1
RT
+ R12 + R13 + ..
1
1
= 6Ω
+ 3Ω
R T = 2Ω
5.42
Se conectan en paralelo las resistencias de 12 Ω y 6 Ω, a una batería de 40 volts, ¿Cuál es
la intensidad de corriente que circula por el circuito?
a) 2.2 A
b) 10 A
c) 3.3 A
d) 6.6 A
Solución .
Datos: R 1 = 12Ω R 2 =6 Ω
1
RT
1
1
1
R 1 + R 2 + R 3 + ..
1
1
1
R T = 12Ω + 6Ω
=
R T = 4Ω
Ademas: I = VR I =
I = 10A
40V
4Ω
5.9
Óptica y acústica
Reflexión y refracción de la luz
La óptica es parte de la física que estudia la luz y aquellos fenómenos que impresionan al sentido de la vista.
Óptica geométrica
Se fundamenta en la teoría de los rayos de luz, la cual considera que todo objeto visible emite
rayos rectos de luz en cada punto de él y en todas direcciones.
Reflexión de la luz
En este fenómeno un rayo luminoso experimenta un cambio de dirección y sentido al chocar
contra la superficie de separación entre 2 medios. Una reflexión regular ocurre cuando la superficie reflectora es lisa y una reflexión irregular cuando la superficie reflectora es rugosa.
Donde: i = ángulo de incidencia r = ángulo de reflexión Leyes de la reflexión
El rayo incidente, la normal y el rayo reflejado se encuentran en un mismo plano.
El ángulo de incidencia es igual al ángulo de reflexión i = r .
Refracción de la luz Un rayo luminoso experimenta un cambio de dirección cuando atraviesa
oblicuamente la superficie entre 2 medios de naturaleza diferente. Cuando un rayo de luz atraviesa la superficie entre dos medios, la frecuencia permanece constante.
Leyes de la refracción
El rayo incidente, la normal y el rayo refractado se encuentran en un mismo plano.
Para 2 medios dados, la relación entre el seno del ángulo de incidencia y el seno del ángulo de refracción es constante.
η=
sen i
sen r
Donde: η = índice de refracción (adimensional) i = ángulo de incidencia r = ángulo de refracción Cuando un rayo de luz pasa de un medio a otro la frecuencia permanece constante.
Índice de refracción de algunas sustancias:
Sustancia
Agua
Aire
Alcohol
Vidrio
Diamante
Índice de refracción η
1.003
1.33
1.36
1.5
2.42
El índice de refracción también puede calcularse con el cociente de las magnitudes de las velocidades del primero y segundo medios, por lo que:
η=
sen i
sen r
=
v1
v2
Donde:
η = índice de refracción (adimensional)
i = ángulo de incidencia
r = ángulo de refracción
v 1 = magnitud de la velocidad de la luz en el primer medio en km/s
v 2 = magnitud de la velocidad de la luz en el segundo medio en km/s
5.43
1.- Un rayo luminoso llega a la superficie de separación entre el aire y el vidrio, con un
ángulo de incidencia de 70°. Calcular el ángulo de refracción.
a) 70°
b) 20°
c) 38.8°
d ) 51.2°
e) 30.5°
Solución .
Datos:
i = 70◦
r =?
η vi d r i o = 1.5
Fórmula:
η=
sen i
sen r
sen r =
−→
sen i
η
Sustitución y resultado:
sen r =
sen 70◦
1.5
sen r =
0.9397
1.5
= 0.6265
r = sen −1 0.6265 = 38.8◦
La respuesta es el inciso c.
5.44
El diamante tiene un índice de refracción η =2.5, ¿Cúal es la velocidad de la luz en el
diamante?
a) 120 000 km/s
b) 300 000 km/s
c) 480 000 km/s
d ) 50 000 km/s
e) 300 km/s
Solución .
Datos:
v 1 = velocidad de la luz en el vacío = 300 000 km/s
η = 2.5
v 2 = velocidad de la luz en el diamante = ?
Fórmula:
η=
v1
v2
−→
v2 =
v1
η
Sustitución y resultado:
v2 =
300 000 km/s
2.5
v 2 =120 000 km/s
La respuesta es el inciso a.
5.45
3.- ¿Cúal es el índice de refracción de un material si en él, la velocidad de la luz es de 240
000 Km/s?
a) 1.5
b) 1.25
c) 2.8
d ) 1.33
e) 2.5
Solución .
Datos:
v 1 = velocidad de la luz en el vacío = 300 000 km/s
η=?
v 2 = velocidad de la luz en el material = 240 000 km/s
Fórmula:
η = vv 12
Sustitución y resultado:
η=
300 000 km/s
240 000 km/s
η = 1.25
La respuesta es el inciso b.
Ondas longitudinales y transversales
Una onda mecánica es una perturbación que se propaga en la materia. Existen dos tipos de
ondas: las transversales y las longitudinales.
Ondas transversales
En ellas las partículas vibran de manera perpendicular a la dirección de propagación de la onda.
Ejemplo: Una onda transversal se forma al hacer vibrar una cuerda fija en uno de sus extremos,
o es aquélla provocada por un cuerpo que cae en el agua tranquila de un estanque.
Ondas longitudinales
En ellas las partículas se mueven en la misma dirección en que se propaga la onda.
Ejemplo: El sonido es una onda longitudinal, al hacer vibrar un resorte también se produce
una onda de este tipo. Elementos de una onda
Donde:
A, B = crestas
C , D = valles
r = amplitud
λ = longitud de onda
Características de una onda
Frecuencia ( f )
Es el número de ondas que pasan por un punto en la unidad de tiempo.
f =
Donde:
f = frecuencia [hertz,
T = periodo [s]
vi b ci cl os 1
s ,
s , s]
1
T
Periodo (T )
Es el tiempo que tarda una onda en pasar por un punto.
T=
Donde:
f = frecuencia [hertz,
1
f
vi b ci cl os 1
s ,
s , s]
T = periodo [s]
Longitud de onda (λ)
Es la distancia que existe entre 2 crestas, 2 valles o 2 partículas en fase consecutiva.
Amplitud
Es el máximo desplazamiento de las partículas de una onda.
Velocidad de propagación (v)
Es la velocidad con que se mueve una onda a través de un medio. La velocidad de una onda sonora (sonido) a una temperatura de 20 °C es de 343.2 m/s, aproximadamente, y conforme
aumenta la temperatura se incrementa su velocidad de acuerdo con la relación v = 331+0.61 T .
La velocidad del sonido en el agua es cuatro veces mayor que en el aire.
v = λ· f
o
v=
λ
T
Donde:
v = Velocidad de propagación [m/s, cm/s, km/s]
T = periodo [s]
f = frecuencia [hertz,
vi b ci cl os 1
s ,
s , s]
λ = longitud de onda [m, cm, km]
5.46
1.- ¿A qué velocidad se propagan las ondas de 5 m de longitud de onda y de 30 hertz de
frecuencia?
a) 15 m/s
b) 0.15 m/s
c) 1500 m/s
d ) 150 m/s
e) 1.5 m/s
Solución .
Datos:
λ=5m
f = 30 hertz
v=?
Fórmula:
v = λ· f
Sustitución y resultado:
v = (5 m)(30 her t z)
v = (5 m)(30 1s )
v = 150 m/s
La respuesta es el inciso d.
5.47
2.- Una persona se encuentra a 420 m de una aparato de sonido, si escucha las notas de
una melodía después de 3 segundos, ¿a qué velocidad viajó el sonido?
a) 140 m/s
b) 1 260 m/s
c) 1 400 m/s
d ) 714 m/s
e) 1.4 m/s
Solución .
m
Datos: λ = 420 m T = 3 s v = ? Fórmula: v = Tλ Sustitución y resultado: v = 420
3 s v = 140
m/s La respuesta es el inciso a. 3.- La cresta de una onda producida en la superficie libre
de un líquido avanza 0.5 m/s. Si tiene una longitud de onda de 4 * 10−1 m/ciclo, calcular
su frecuencia.
a) 2 x 10−1 ciclos/s
b) 1.25 ciclos/s
c) 80 ciclos/s
d ) 8 ciclos/s
e) 4 ciclos/s
Solución:
Datos:
λ = 4 x 10−1 m/ciclo
v = 0.5 m/s
f =?
Fórmula:
v = λ· f
−→ f =
v
λ
Sustitución y resultado:
f =
0.5 m/s
4 x 10−1 m/ci cl o
f = 1.25 ciclos/s
La respuesta es el inciso b.
6
Probabilidad y Estadística
Estadística descriptiva
La estadística descriptiva está formada por procedimientos empleados para resumir y describir
las características importantes de un conjunto de mediciones. Ésta a su vez trata de la selección, análisis y uso de datos con el fin de resolver problemas. Toda persona, tanto en su ejercicio profesional como en su actividad diaria, se encuentra en contacto con revistas, televisión y
otros medios de comunicación, donde se le ofrece información a través de datos. Consecuentemente, algunos conocimientos de estadística le serán de utilidad a la población en general,
pero en particular, el conocimiento estadístico será vital para ingenieros, científicos y administradores debido a que de manera rutinaria, manejan y analizan datos.
Definición 6.1
Población
Una población es el conjunto de mediciones de interés para el investigador.
Definición 6.2
Muestra
Una muestra es un subconjunto de mediciones seleccionado de la población de interés.
Existen a su vez algunos tipos de variables a considerar dentro de la estadística descriptiva. A
continuación, se enlistan y definen:
* Cuantitativas: Las variables cuantitativas miden una cantidad numérica en cada unidad experimental (entiéndase por unidad experimental el individuo u objeto en el que se mide una
variable).
* Cualitativas: Las variables cualitativas miden una cualidad o característica en cada unidad
experimental.
* Discretas: Una variable discreta es aquella puede tomar sólo un número finito o contable de
valores. Por ejemplo, tenemos el número de autos que ingresan a un autolavado (1, 2, 4, 6, 9).
El nombre de discreta se refiere a las brechas discretas entre los posibles valores que la variable
puede tomar.
* Continuas: Una variable continua puede tomar infinitamente muchos valores correspondientes a los puntos en un intervalo de recta. Por ejemplo, tenemos el registro de la temperatura
corporal de 5 individuos (36.1°C, 36.4°C, 37.1°C, 36.56°C, 36.7°C). Como puede observar, variable como: la estatura, peso, tiempo, distancia y temperatura son continuas porque pueden
tomar valores en cualquier punto a lo largo de un intervalo de recta.
Probabilidad y Estadística
6.1
170
Nivel de medición de las variables. El nivel de medición se refiere a la relación entre los valores
que se asignan a los atributos de una variable.
Los números se pueden agrupar en 4 tipos o niveles: nominal, ordinal, por intervalos y de razón.
Nivel de medición nominal: El nivel nominal es apenas una medida. Se refiere a la cualidad
más que a la cantidad. Un nivel nominal de medición es simplemente una cuestión de diferenciar por nombre, por ejemplo, 1= hombre, 2= mujer. Aunque estamos usando los números 1 y
2, estos no indican cantidad. La categoría binaria de 0 y 1 utilizada para las computadoras es
un nivel nominal de medición.
Ejemplo de nivel de medición nominal:
Preferencia religiosa: 1= Budista, 2= Musulmana, 3= Cristiana, 4= Judía, 5= Otra
Nivel de medición ordinal: Este nivel se refiere al orden en la medición. Una escala ordinal
indica la dirección, además de proporcionar información nominal. Bajo/Medio/Alto o Más Rápido/Más Lento son ejemplos de niveles ordinales de medición. Calificar una experiencia con
un 9 en una escala de 1 a 10 nos indica que fue mejor que una experiencia calificada con un 6.
Muchas escalas o pruebas psicológicas utilizan la escala ordinal de medición.
Algunos ejemplos medición ordinal:
Clasificación: 1er lugar, 2do lugar, último lugar Nivel de acuerdo: No, Tal vez, Sí
Nivel de medición por intervalo: La escala de intervalo proporcionan información sobre el orden y también poseen intervalos iguales. Del ejemplo anterior, si supiéramos que la distancia
entre 1 y 2 es la misma que entre 7 y 8 en nuestra escala de calificación de 10 puntos, entonces
tendríamos una escala de intervalo.
Un ejemplo de una escala de intervalo es la temperatura, medida en una escala Fahrenheit o
Celsius. Un grado representa la misma cantidad subyacente de calor, independientemente de
dónde ocurra en la escala. Si lo medimos en unidades Fahrenheit, la diferencia entre una temperatura de 46 y 42 es la misma que la diferencia entre 72 y 68. Las escalas de medición de
intervalos iguales pueden ser utilizadas para medir opiniones y actitudes.
Ejemplo de niveles de medición de intervalo:
Hora del día en un reloj de 12 horas. Intervalo de tiempo de día, intervalos iguales; reloj analógico (12 horas), la diferencia entre la 1 y 2 pm es la misma que la diferencia entre las 11 y 12 am.
Representaciones gráficas. Una vez recolectados los datos, éstos pueden consolidarse y resumirse para mostrar la siguiente información:
* ¿Qué valores de la variable han sido medidos?
* ¿Con qué frecuencia se presenta cada uno de los valores?
Para este fin, se puede construir una tabla estadística que se puede usar para mostrar los datos
gráficamente como una distribución de datos. El tipo de gráfica que se escoja depende del tipo
de variable que se haya medido. Cuando la variable de interés es cualitativa, la tabla estadística
es una lista de las categorías siendo consideradas junto con una medida de la frecuencia con
que se presenta cada valor. Se puede medir la frecuencia en tres formas diferentes:
* La frecuencia o número de mediciones en cada categoría
* La frecuencia relativa o proporción de mediciones en cada categoría
* El porcentaje de mediciones en cada categoría
Por ejemplo, si con n representamos el número total de mediciones en el conjunto, se puede
hallar la frecuencia relativa y porcentaje usando estas relaciones:
Se encontrará que la suma de las frecuencias es siempre n, la suma de las frecuencias relativas
es 1 y la suma de los porcentajes es 100 por ciento. Las categorías para una variable cualitativa
deben escogerse de modo que:
una medición pertenecerá a una categoría y sólo a una cada medición tiene una categoría a la
que se puede asignar.
Por ejemplo, si se pueden clasificar productos cárnicos de acuerdo con el tipo de carne utilizada, se pueden usar estas categorías: carne de res, pollo, marisco, carne de puerco, pavo, otra.
Para clasificar rangos de la facultad de una escuela, se pueden usar estas categorías: profesor,
profesor adjunto, profesor auxiliar, instructor, conferenciante, otro. La categoría otro está incluida en ambos casos para tomar en cuenta la posibilidad de que una medición no se pueda
asignar a una de las categorías anteriores.
Una vez que a las mediciones se les hayan dado categorías y se resumieron en una tabla estadística, se puede usar ya sea una gráfica de pastel o una gráfica de barras para mostrar la
distribución de los datos. Una gráfica de pastel es la conocida gráfica circular que muestra la
forma en que están distribuidas las medidas entre las categorías. Una gráfica de barras muestra
la misma distribución de medidas en categorías, con la altura de la barra midiendo la frecuencia con la que se observa una categoría en particular.
6.1
Conversiones
En una encuesta respecto a la educación pública, a 400 administradores de escuelas se
les pidió calificaran la calidad de la educación en Estados Unidos. Sus respuestas están
resumidas en la tabla 1. Construya una gráfica de pastel, una gráfica de barras y una ojiva
a partir de este conjunto de datos.
Solución .
Para construir una gráfica de pastel, asigne un sector de círculo a cada categoría. El ángulo de cada sector debe ser proporcional a la magnitud de las mediciones (o frecuencia
relativa) en esa categoría. Como un círculo contiene 360°, se puede usar esta ecuación
para hallar el ángulo:
El impacto visual de estas 3 gráficas es un poco diferente. La gráfica de pastel se usa
para mostrar las relaciones de las partes con respecto al todo; la gráfica de barras se usa
para destacar la cantidad real o frecuencia para cada categoría; la ojiva muestra la curva
de una función de distribución acumulativa. Como las categorías en este ejemplo son
calificaciones ordenadas (A, B, C, D), no desearíamos reacomodar las barras de la gráfica
para cambiar su forma. En una gráfica de pastel, el orden de presentación es irrelevante.
El histograma de frecuencia relativa, para un conjunto de datos cuantitativos es una gráfica de
barras en la que la altura de la barra muestra con qué frecuencia (medida como proporción
o frecuencia relativa) las mediciones caen en una clase o subintervalo particular. Las clases o
subintervalos se grafican a lo largo del eje horizontal.
Ejemplo:
6.2
Histograma
Los datos de la tabla 2 son los pesos de 30 bebés de gestación completa al momento de
nacer. Se desea realizar un histograma que permita analizar de forma gráfica estos pesos.
Solución .
Como regla práctica, el número de clases debe ser de 5 a 12; cuantos más datos haya,
más clases se requieren. Las clases deben ser escogidas para que cada una de las
mediciones caiga en una clase y sólo en una. Para los pesos al nacer que se muestran
en la tabla 2, decidimos usar intervalos de peso de igual longitud. Como el intervalo de
pesos al nacer es
Ahora, dividimos el intervalo de las mediciones más pequeñas a las más grandes en
subintervalos o clases de igual longitud (0.5 de longitud para un total de 8 clases seleccionadas). Si se ponen en columna los puntos de cada subintervalo y se traza una barra
sobre cada una de las columnas, se habrá creado un histograma de frecuencia o un
histograma de frecuencia relativa, dependiendo de la escala del eje vertical. Empezando
el primer intervalo al valor más bajo, 5.6, formamos subintervalos de 5.6 hasta, pero
no incluyendo 6.1, 6.1 hasta, pero no incluyendo 6.6, y así sucesivamente. Usando el
método de inclusión izquierda e incluyendo el punto de frontera de clase izquierda pero
no el punto de frontera derecha en la clase, eliminamos cualquier confusión acerca de
dónde poner una medición que resulte caer en un punto de frontera de clase.
6.2
Probabilidad
Introducción
La probabilidad surge de la necesidad de predecir cuánto se podría ganar o perder en los diferentes juegos de azar. Por esta razón, en un principio se acostumbra explicar los problemas
de probabilidad utilizando esos juegos; sin embargo, no todos los ejemplos que utilizaremos
para explicar las reglas de probabilidad han sido tomados de los juegos de azar. La probabilidad básica se utiliza para evaluar la probabilidad de ocurrencia de diferentes eventos o sucesos
(fenómenos). Con la probabilidad básica pueden hacerse inferencias de una muestra hacia
una población. La probabilidad es una medida numérica de la posibilidad de que ocurra un
evento. La escala de los valores posibles de probabilidad se ubica siempre entre cero y uno. La
probabilidad de cero significa que es difícil que el evento ocurra; cuando es de 0.5 indica que
es probable que ocurra, o bien, que no ocurra. Si la probabilidad es de uno, entonces es seguro
que el evento ocurrirá, ver Figura 6.1.
Figura 6.1. Escala de valores de la probabilidad
La probabilidad de acuerdo a su interpretación se clasifica como objetiva y subjetiva. La probabilidad objetiva se clasifica como probabilidad clásica o empírica, tal como se observa en la
Figura 6.2.
Figura 6.2. Clasificación de la probabilidad
La probabilidad objetiva clásica se basa en la consideración de que los resultados posibles de
un experimento tienen la misma probabilidad de ocurrir. Para calcular la probabilidad de que
ocurra el evento (A), se requiere determinar el número de veces que se quiere que aparezca
dicho evento (A), entre el total de resultados posibles del experimento.
Ejemplos: - Lanzamiento de una moneda - Lanzamiento de un dado.
6.3
Lanzamiento de un dado
Se lanza un dado, cuál será la probabilidad de obtener un número par.
Solución .
- Número de resultados favorables será que se obtenga 2,4 y 6. - Número de resultados
posibles serán, 1,2,3,4,5 y 6. La probabilidad estará indicada de la siguiente manera:
La probabilidad objetiva empírica o probabilidad bajo el enfoque de frecuencia relativa es
aquella que se presenta observando la frecuencia con la que un evento (A), ha sucedido en
el pasado y se puede representar de la siguiente manera:
6.4
Probabilidad
Se registraron en la siguiente tabla, los últimos 10 resultados del equipo de Fut-bol Morelia.
Calcular la probabilidad de que el siguiente encuentro gane su partido.
Solución .
En aquellas situaciones donde no se tiene información para poder aplicar una frecuencia relativa, ni es posible aplicar tampoco una probabilidad clásica, se recurre a una evaluación dada
en general por algún experto en el tema en cuestión, llamándose a ésta una probabilidad subjetiva.
La estadística se divide en dos grandes áreas que son la estadística descriptiva e inferencial,
dividiéndose esta última en estimación de parámetros y pruebas de hipótesis, tal como se observa en la siguiente imagen.
La estadística es el arte y ciencia de reunir, analizar presentar e interpretar datos, así como
elaborar principios y métodos que nos ayuden a tomar decisiones frente a la incertidumbre.
La estadística descriptiva estudia las características de un conjunto de datos para conocer los
valore que los describen, tales como la media, varianza, desviación estándar, moda, etc. La
estadística inferencial analiza los datos de una muestra aleatoria a fin de hacer predicciones o
generalizaciones acerca de las características de una población.
En la teoría de conjuntos existen algunos conceptos indispensables para poder entenderla y
éstos se enuncian a continuación:
Experimento, es cualquier proceso en el cual se generan resultados en forma aleatoria.
Espacio muestral, son todos los resultados posibles que se pueden obtener del experimento.
Evento, es uno o varios resultados contenidos en el espacio muestral. Es un subconjunto del
espacio muestral.
Evento simple es aquel que está constituido por un solo resultado del experimento.
Ejemplo: Considere el experimento de verificar tres productos clasificando a cada uno de ellos
como defectuoso (D) o no defectuoso (N).
El espacio muestral (S), estará conformado por:
EVENTO MUTUAMENTE EXCLUYENTES O EXCLUSIVOS: Son aquellos eventos en los cuales
la ocurrencia de uno, excluye la ocurrencia del otro. No pueden ocurrir al mismo tiempo.
EVENTOS NO EXCLUYENTES: Son aquellos eventos que si pueden ocurrir al mismo tiempo.
En este caso uno de los resultados se encuentra en ambos eventos.
- Ley aditiva para la unión de dos eventos:
6.5
¿Cuál es la probabilidad de obtener un total de 7 u 11 como suma cuando se lanza un par
de dados?
Solución .
Sea A el evento de que ocurra 7 y B el evento de que ocurra 11. Entonces, un total de
7 ocurre para 6 de los 36 puntos muestrales y un total de 11 ocurre solo para 2. Como
todos los puntos muestrales son igualmente probables, tenemos P(A)= 1/6 y P(B)= 1/18.
Los eventos A y B son mutuamente excluyentes, pues un total de 7 y 11 no pueden ocurrir
en el mismo lanzamiento. Por lo tanto,
6.6
Al final del semestre, Juan se va a graduar en la facultad de ingeniería industrial en el
tecnológico de Morelia. Después de tener entrevistas con dos compañías donde quiere
trabajar, el evalúa la probabilidad que tiene de lograr una oferta de empleo en la compañía A como 0.8, y la probabilidad de obtenerla de la compañía B como 0.6. Si, por otro
lado, considera que la probabilidad de que reciba ofertas de ambas compañías es de 0.5
¿Cuál es la probabilidad de que obtendrá al menos una oferta de esas dos compañías?
Solución .
Usando la regla aditiva:
EVENTOS DEPENDIENTES: Son aquellos eventos en los cuales la ocurrencia de uno influye en
la ocurrencia de otro. - Ley multiplicativa para la intersección de dos eventos: Si los eventos
son dependientes deberá cumplirse lo siguiente:
6.7
Definiendo los siguientes eventos:
Deberá cumplirse la siguiente condición para que los eventos sean dependientes:
Solución .
Verificando esta condición:
EVENTOS INDEPENDIENTES: Son aquellos eventos en los cuales la ocurrencia de uno de ellos
no influye en la ocurrencia del otro.
Si los eventos son independientes deberá cumplirse:
6.8
Definiendo los siguientes eventos:
Deberá cumplirse la siguiente condición para que los eventos sean independientes:
Solución .
Verificando esta condición:
Nota: La dependencia o independencia de dos eventos no se pueden observar a simple
vista como en el caso de los eventos mutuamente excluyentes, por lo que habría que
verificar que se cumplan las condiciones indicadas en los ejemplos anteriores.
EVENTOS COLECTIVAMENTE EXHAUSTIVOS: Son aquellos eventos cuya unión de
todos ellos forman en espacio muestra.
Como son eventos mutuamente excluyentes se tendrá lo siguiente:
Se puede observar en lo anterior que la unión de los dos eventos, conforman la
totalidad del espacio muestral.
TEOREMA DE BAYES.
El teorema de Bayes se deriva del análisis de la probabilidad en la intersección de dos
eventos dependientes.
Igualando 1 y 2
despejando P(A/B), se tiene la siguiente ecuación, la cual se le conoce como Teorema de
Bayes,
6.9
La empresa de plásticos del hogar tiene pensado introducir en el mercado una nueva
línea de recipientes de plástico para horno de microondas. La experiencia que tiene la
empresa al introducir en el mercado un nuevo producto es que 60 % de las veces, este
tiene una excelente aceptación y 40 % de las veces ha tenido una mediana aceptación.
El gerente de la empresa decide hacer un estudio de mercado antes de fabricar y lanzar
al mercado la nueva línea de recipientes de plástico para microondas, y saber si es
recomendable fabricarlo o no. En el pasado 25 % de los recipientes de plástico con
la aceptación media recibió del estudio del mercado un informe favorable, mientras
que 65 por ciento de los recipientes de plástico con excelente aceptación recibió un
resultado favorable. El gerente de mercadotecnia desea conocer la probabilidad de que
la nueva línea de recipientes de plástico tendrá una aceptación excelente, dado que en
el estudio de mercado tiene un informe favorable.
Solución .
Sucesos:
F: recibe informe favorable.
A: línea de recipientes con aceptación excelente.
B: línea de recipientes con aceptación media.
El primer paso es establecer el espacio muestral, auxiliándose de un diagrama ven. Del
espacio muestral se deducen las probabilidades en la siguiente tabla:
Espacio muestral.
El suceso F asociado con el espacio muestral representa el informe favorable del estudio
de mercado.
La probabilidad de seleccionar un recipiente de plástico con expectación excelente o
media, dado que el estudio de mercado tiene un informe favorable.
La probabilidad de que la nueva línea de recipientes de plástico tendrá una aceptación
excelente, dado que el estudio de mercado tiene un informe favorable. La probabilidad
se calcula utilizando el teorema de Bayes.
El teorema de Bayes para tres eventos está dado por la siguiente ecuación.
6.10
En un laboratorio de mezclas, tres químicos, Q1, Q2 y Q3, montan 30, 45 y 25 por ciento de mezclas, respectivamente. Se sabe que 2, 3 y 2 por ciento de las mezclas hechas
por cada químico, respectivamente, tienen defectos. Si se elige al azar una mezcla y se
encuentra que esta defectuosa, ¿Cuál es la probabilidad de que esta mezcla haya sido
hecha por el químico Q3?
Solución .
Aplicando la fórmula se tiene:
Con los cálculos anteriores se da respuesta a la pregunta del problema y se tiene
entonces que la probabilidad de que la mezcla defectuosa la haya elaborado el químico
3 es de 0.2041.
Los eventos en este teorema deben ser mutuamente excluyentes y colectivamente
exhaustivos, como se puede observar en los eventos Q1, Q2 y Q3.
6.3
Variables Aleatorias
Una variable aleatoria es una función de valor real definida sobre un espacio muestral. Una variable aleatoria se puede utilizar para definir eventos numéricos que son de interés en un experimento. Las variables aleatorias se dividen en discretas y continuas. Las discretas son aquellas
que pueden tomar solo un número finito o contablemente infinito de valores distintos, como
por ejemplo el número de teléfonos celulares defectuosos en una venta de 200 celulares. Las
variables aleatorias continuas pueden adquirir valores que se encuentre entre intervalos (finitos o infinitos) de números reales como, por ejemplo, el peso de los estudiantes de 4° semestre
de Ingeniería Industrial o el tiempo que tardan en llegar a la universidad 15 alumnos que viven
por rumbos similares. El valor esperado, media o esperanza matemática de una variable aleatoria es el valor medio del experimento que representa la variable aleatoria. Y la varianza es
una medida de dispersión que nos dice que tan variables son los datos del experimento, pero
respecto a su media o valor esperado.
REACTIVOS
1. Del evento, venta de vehículos en la exposición anual 2022 de vehículos, la variable aleatoria
discreta puede ser:
a) Vehículos exhibidos en la expo
b) No. de vehículos vendidos en la expo r espuest a − cor r ec t a
c) No. de personas que visitaron la expo
d ) No. exposiciones
e) Ninguna de las anteriores
2. Del evento, predicción del clima de la ciudad de Morelia durante el verano, la variable aleatoria continua puede ser:
a) La temperatura ambiental en °C r espuest a − cor r ec t a
b) No. de días lluviosos
c) No. de días en verano
d ) No. exposiciones
e) Ninguna de las anteriores
3. El valor esperado de una distribución de probabilidad discreta f (x), se determina por E (x) =
P
x( f x). El valor esperado de la siguiente distribución de probabilidad es:
a) 1.7 r espuest a − cor r ect a
b) 1
c) 3.5
d) 3
e) 3.6
4. La función f (x) es una función de densidad de probabilidad para la variable aleatoria X,
definida sobre el conjunto de números reales, si cumple con la condición mostrada, la siguiente
es una función de densidad de probabilidad:
A continuación se muestra el procedimiento:
a) Falso
b) Verdadero r espuest a − cor r ect a
c) Tal vez
d ) Incierto
e) Ninguna de las anteriores
5. El siguiente enunciado es:
“Cuando se realizan estudios estadísticos, los datos que se obtienen son mediciones que se
pueden representar en diferentes escalas, es decir el resultado se puede asumir en diferentes
valores, que además se observan mediante procedimientos al azar, a esto se le llama variable
aleatoria y a su vez esta variable aleatoria se puede clasificar en discreta o continua”.
a) Falso
b) Verdadero r espuest a − cor r ect a
c) Tal vez
d ) Incierto
e) Ninguna de las anteriores
6.4
DISTRIBUCIONES DE PROBABILIDAD-Discretas
Una distribución de probabilidad muestra todos los posibles valores que se pueden presentar en un experimento y muestra cómo se distribuyen los valores de la variable aleatoria. Una
distribución describe la probabilidad de que un evento se presente en el futuro.
6.11
Distribución de probabilidad
Experimento: Seleccionar dos bolas de helado entre dos sabores (vainilla y chocolate),
donde la selección de cada sabor tiene la misma probabilidad de ocurrir.
Solución .
Variable: Cantidad de bolas de helado sabor chocolate
CARACTERÍSTICAS DE UNA DISTRIBUCIÓN DE PROBABILIDAD
1. La probabilidad de un resultado del experimento toma valores entre 0 y 1, inclusive.
2. Los resultados de un experimento son eventos mutuamente excluyentes.
3. La suma de todas las probabilidades de los eventos simples de un experimento es igual a 1.
Una variable aleatoria es el resultado que se puede presentar al azar en cualquier experimento
aleatorio. Ejemplo, cuando lanzamos un dado de forma aleatoria, obtenemos seis posibles resultados, donde el valor obtenido en la cara superior es la variable aleatoria y toma valores del
1 al 6.
CLASIFICACIÓN DE LAS DISTRIBUCIONES DE PROBABILIDAD
- Distribuciones Discretas
- Binomial
- Poisson
- Distribuciones Continuas
- Normal
- Exponencial
PROPIEDADES DE UNA DISTRIBUCIÓN DE PROBABILIDAD BINOMIAL
1. El experimento consiste en una serie de n ensayos idénticos.
2. En cada ensayo hay dos resultados posibles. A un resultado se le llama éxito y al otro se le
llama fracaso (el éxito es la característica buscada en el experimento).
3. La probabilidad de éxito se le denomina p, y no cambia de un ensayo a otro. La probabilidad
de fracaso, que se denota q = 1 -p, tampoco cambia de un ensayo a otro.
4. Los ensayos son independientes.
6.12
experimento binomial
Si un experimento consiste en lanzar 3 monedas y registrar la cantidad de águilas
obtenidas. Cada ensayo es el lanzamiento de una moneda, por lo tanto, se realizan 3
ensayos. Cada vez que se lanza una moneda se pueden tener dos resultados posibles,
obtener águila o sol. Donde el éxito será el águila, de acuerdo con la definición del
experimento.
Solución .
contenidos...
Se asume que la moneda no está cargada, y los resultados son igualmente posibles; se
define que la probabilidad de éxito p= 0.50 y la probabilidad de fracaso q= 0.50.
Los ensayos o lanzamientos son independientes porque al resultado de un ensayo no le
afecta lo que pase en los otros ensayos o lanzamientos.
La variable aleatoria X tomará valores de: 0, 1, 2 o 3.
Distribución de probabilidad de lanzar 3 monedas y registrar la cantidad de águilas
obtenidas.
Fórmulas para una distribución binomial
La probabilidad de encontrar exactamente 2 águilas en 3 lanzamientos utilizando la
fórmula:
Si requerimos conocer la probabilidad acumulada entre 0 y 2 debemos sumar las
probabilidades de cada entero:
Ejercicio 1 Sea x una variable aleatoria binomial con n = 7, p = .3.
Encuentre estos valores: q= 0.7. Encuentre la P (x = 4)
a) (7C 4) ∗ (.33 ) ∗ (.74 )
b) (4C 7) ∗ (.34 ) ∗ (.73 )
c) (7C 4) ∗ (.34 ) ∗ (.73 ) r espuest a − cor r ec t a
d ) (7C 4) ∗ (.35 ) ∗ (.73 )
e) Ninguna de las anteriores
Solución:
Ejercicio 2 Una encuesta el Hotel Pacific preguntó: ?Cuando usted viaja al extranjero, ¿suele
aventurarse usted solo o prefiere permanecer con el grupo de su tour?? Se encontró que 23 %
prefiere permanecer con el grupo de su tour. ¿Cuál es la probabilidad de que, en una muestra
de seis viajeros, dos prefieran permanecer con su grupo?
a) 28 r espuest a − cor r ect a
b) 23
c) 50
d ) 60
e) Ninguna de las anteriores
Solución:
Ejercicio 3 Calcule la desviación estándar de una distribución binomial, donde n= 10, p= 0.1
a) 0.90
b) 0.95 r espuest a − cor r ect a
c) 0.96
d ) 0.97
e) 0.99
Solución:
Ejercicio 4 El sistema de seguridad de una casa está diseñado para tener un 99 % de contabilidad. Suponga que nueve casas equipadas con este sistema de seguridad experimentan un
intento de robo. Encuentre la probabilidad de que más de siete de las alarmas se activaron.
a) P (X > 7) = P 7 + P 8 + P 9
b) P (X > 7) = P 8 + P 9 + P 10
c) P (x > 7) = P 8 + P 9 r espuest a − cor r ec t a
b) P (X > 7) = P 7 + P 8 + P 9 + P 10
d ) Ninguna de las anteriores
Solución:
PROPIEDADES DE UNA DISTRIBUCIÓN DE PROBABILIDAD DE POISSON
Distribución de probabilidad para datos que representa el número de sucesos de un evento
determinado en una unidad de tiempo o espacio.
Los eventos en una distribución Poisson ocurren al azar e independientemente unos de otros.
Los eventos se definen como “infinitos”, por lo cual es apropiado usar el complemento para
determinar una probabilidad mayor a x.
x representa el número de eventos que ocurren en un periodo o espacio, durante el cual se puede esperar que ocurra un promedio de µ de estos eventos.
La probabilidad de ocurrencia es la misma para cualquier intervalo de la misma magnitud.
FÓRMULAS PARA UNA DISTRIBUCIÓN POISSON
Sea µ el número promedio de veces que ocurre un evento en cierto tiempo o espacio. La probabilidad de k sucesos de este evento para valores de k = 0, 1, 2, 3, ?. Donde, k= eventos buscados
que ocurran en un periodo, µ = tasa media de ocurrencia en un periodo de tiempo o espacio.
6.13
Distribución Poisson
En un aeropuerto se registran en promedio 5 accidentes por mes en la región sur. Encuentre la probabilidad de que durante un mes determinado no haya accidentes en la
región sur.
Solución .
contenidos...
Si necesitamos cambiar la unidad de tiempo en la tasa de media de ocurrencias
hacemos lo siguiente:
¿Cuál será la tasa esperada de accidentes en un año?
¿Cuál será la tasa media de que ocurran accidentes en 1 día?
Ejercicio 1
Durante el ciclo escolar los accidentes en menores incrementan. Si el número promedio de
lesiones por año para niños en edad escolar es de dos, ¿cuál es la probabilidad de que un niño
sufra 2 lesiones durante un año?
a) 0.44
b) 0.27 r espuest a − cor r ect a
c) 0.73
d ) 0.88
e) 0.98
Solución:
Ejercicio 2
El número de personas ingresadas a una unidad de cuidados intensivos en el hospital general
tiene una distribución de probabilidad de Poisson con media igual a cinco pacientes por día.
¿Cuál es la probabilidad de que el número de personas ingresadas a una unidad de cuidados
intensivos en el hospital general en un día sea menor o igual a dos?
a) 12 r espuest a − cor r ect a
b) 22
c) 44
d ) 88
e) 98
Solución:
6.5
DISTRIBUCIONES DE PROBABILIDAD-Continuas
Distribución de probabilidad normal
La distribución de probabilidad más comúnmente usada para describir una variable aleatoria
continua es la distribución de probabilidad normal. Se usa en una amplia variedad de aplicaciones en variables aleatorias como: la altura y el peso de las personas, las calificaciones de los
exámenes, las mediciones científicas, la precipitación pluvial y otros valores parecidos. También tiene un uso muy extendido en la inferencia estadística.
Curva normal La forma de la distribución normal se representa por medio una curva con forma de campana. La función de densidad de probabilidad que define la curva de la distribución
normal se muestra en seguida.
Figura 1 Curva de la distribución normal
Observaciones acerca de las características de la distribución normal.
1. La familia completa de distribuciones normales se diferencia por medio de dos parámetros:
la media µ y la desviación estándar σ.
2. El punto más alto de una curva normal se encuentra sobre la media, el cual coincide con
la mediana y la moda de la distribución.
3. La media de una distribución normal puede tener cualquier valor numérico: negativo, cero o positivo.
4. La distribución normal es simétrica y los extremos de la curva normal se extienden hacia
el infinito en ambas direcciones y en teoría nunca tocan el eje horizontal.
5. La desviación estándar determina qué tan plana y ancha es la curva normal.
6. Las probabilidades para la variable aleatoria normal están representadas por las áreas bajo la curva normal. El área total bajo la curva de una distribución normal es 1.
7. Los porcentajes de los valores en algunos intervalos de uso común son los siguientes.
a) 68.3 % de los valores de una variable aleatoria normal se sitúan más o menos a una desviación estándar de su media.
b) 95.4 % de los valores de una variable aleatoria normal se encuentran más o menos a dos desviaciones estándar de su media.
c) 99.7 % de los valores de una variable aleatoria normal están más o menos dentro de tres desviaciones estándar de su media.
Distribución de probabilidad normal estándar
Se dice que una variable aleatoria que muestra una distribución normal con una media de cero y una desviación estándar de uno tiene una distribución de probabilidad normal estándar.
La letra z se usa comúnmente para designar esta variable aleatoria normal. Como ocurre con
otras variables aleatorias continuas, los cálculos de la probabilidad con cualquier distribución
normal se efectúan al obtener las áreas bajo la gráfica de la función de densidad de probabilidad. Por tanto, para encontrar la probabilidad de que una variable aleatoria normal esté dentro
de cualquier intervalo específico, debe calcularse el área bajo la curva normal en ese intervalo.
Para la distribución normal estándar, las áreas bajo la curva normal ya se han estimado y están
disponibles en tablas que se utilizan para el cálculo de probabilidades.
Problema 1.
Dado que Z es una variable aleatoria normal estándar, calcule las probabilidades siguientes:
Problema 2.
En enero de 2020, los empleados del servicio público pasan un promedio de 77 horas conectados a Internet mientras trabajan. Suponga que la media poblacional es 77 horas, los tiempos
están distribuidos normalmente y la desviación estándar es de 20 horas. a) ¿Cuál es la probabilidad de que en enero de 2003 un empleado seleccionado al azar pasara menos de 50 horas
conectado a Internet?
Respuesta.
Problema 3
Una persona debe estar en el 2 % más alto de la población en una prueba de IQ para aspirar a
la membresía en la sociedad internacional de IQ alto. Si las calificaciones del IQ están normalmente distribuidas con una media de 100 y una desviación estándar de 15, ¿qué puntaje debe
tener una persona que desea calificar para ser miembro de dicha sociedad?
Una persona debería de tener al menos 130.75 de IQ para ser del 2 % mas alto y pertenecer a la
sociedad internacional de IQ alto.
Distribución de probabilidad exponencial
La distribución de probabilidad exponencial puede usarse para variables aleatorias como el
tiempo entre la llegada de un automóvil a un autolavado, el tiempo requerido para cargar un
camión, la distancia entre los defectos importantes de una carretera. Al igual que con la distribución de probabilidad continua, el área bajo la curva correspondiente a un intervalo proporciona la probabilidad de que la variable aleatoria asuma un valor en ese intervalo. Una propiedad de la distribución exponencial indica que la media de la distribución y la desviación
estándar de la distribución son iguales.
Problema 1.
El tiempo entre las llegadas de los vehículos en un autolavado sigue una distribución de probabilidad exponencial con una media de 12 minutos.
a) ¿Cuál es la probabilidad de que el tiempo de llegada entre los vehículos sea de 12 o menos
minutos?
b) ¿Cuál es la probabilidad de que este tiempo sea de 6 o menos minutos?
c) ¿Cuál es la probabilidad de 30 o más minutos entre las llegadas de vehículos?
Respuestas
Problema 2
Mastercable es la compañía de televisión por cable más grande de México. La empresa, generalmente conocida por su calidad y servicio confiable, experimenta periódicamente interrupciones de servicio inesperadas. El 14 de enero de 2020, una interrupción de este tipo ocurrió
para los clientes que vivían en Michoacán. Cuando los clientes llamaron a la oficina de Mastercable, un mensaje grabado les dijo que la empresa estaba al tanto del corte del servicio y que se
anticipaba que éste sería restablecido en dos horas. Suponga que dos horas es el tiempo medio
para efectuar la reparación y que el tiempo de reparación tiene una distribución de probabilidad exponencial.
a) ¿Cuál es la probabilidad de que el servicio de cable sea reanudado en una hora o menos?
b) ¿Cuál es la probabilidad de que la reparación tarde entre una y dos horas?
c) Para un cliente que llama a la oficina de Mastercable a la 10:00 a.m., ¿cuál es la probabilidad
de que el servicio de cable no se haya reanudado todavía a las 2:00 p.m.?
Respuestas:
Docentes participantes
198
[1] Heber ortega Vargas
[2] Alfredo Morales Hernández
[4] Miguel Venegas Espinoza
[5] Rogelio Vences Hernández
[6] Luis Enrique Tapia Chávez
[7] Míriam González Macias
[8] Nidia Torres Vidales
[9] José luis Calderón Durán
[10] Valentín Blanco Bustamante
[11] Luis Enrique Tapia Chávez
[12] José Alfredo González Linares
[13] Vannya Isabel González Nambo
[14] Alejandro Aburto Bedolla
[15] Victor Hugo Estrada Silva
[16] Gabriel Villaseñor Aguilar
Administración
[17] Liliana Patricia Ferreyra Herrera
[18] Martha Estefanía Pérez Mendoza
[19] Victor Hugo Estrada Silva
[20] Gabriel Villaseñor Aguilar
Probabilidad y Estadística
[3] Ramiro Martínez Cámara