ARBOLES

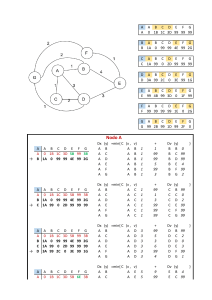
ARBOLES
ALGORITMO Y ESTRUCTURA DE DATOS
Definición
• Desde el punto de vista conceptual, un árbol es un objeto que
comienza con una raíz (root) y se extiende en varias ramificaciones o
líneas (edges), cada una de las cuales puede extenderse en
ramificaciones hasta terminar, finalmente en una hoja.
• Los árboles representan las estructuras no-lineales y dinámicas de
datos más importantes en computación. Dinámicas, puesto que la
estructura árbol puede cambiar durante la ejecución de un programa.
No- lineales, puesto que a cada elemento del árbol pueden seguirle
varios elementos.
Propiedades
En la ciencia de la computación definimos un árbol como un conjunto de
nodos y líneas. Un nodo es un elemento de información que reside en el
árbol. Una línea es un par de nodos ordenados <u,v>, y a la secuencia de
líneas se le denomina ruta (path).
Los árboles tienen las siguientes propiedades:
• Tienen un nodo al que se le llama raíz del árbol.
• Todos los nodos, excepto la raíz, tienen una sola línea de entrada (el nodo
raíz no tiene ninguna).
• Existe una ruta única del nodo raíz a todos los demás nodos del árbol.
• Si hay una ruta <a,b>, entonces a „b‟ se le denomina „hijo‟ de „a‟ y es el
nodo raíz de un subárbol.
LONGITUD DE CAMINO INTERNO Y EXTERNO.
Se define la longitud de camino X como el número de arcos que deben
ser recorridos para llegar desde la raíz al nodo X. Por definición la raíz
tiene longitud de camino 1, sus descendientes directos longitud de
camino 2 y así sucesivamente.
Longitud de Camino Interno
• La longitud de camino interno es la suma de las longitudes de camino
de todos los nodos del árbol. Es importante por que permite conocer
los caminos que tiene el árbol. Puede calcularse por medio de la
siguiente fórmula:
ℎ
𝐿𝐶𝐼 =
• donde
𝑛𝑖 ∗ 𝑖
𝑖=1
• “i” representa el nivel del árbol,
• “h‟ su altura y
• “ni‟ el número de nodos en el nivel “i‟.
Media de la Longitud de Camino Interno
(LCIM)
• Se calcula dividiendo la LCI entre el número de nodos del árbol (n).
LCIM = LCI / n
• Y significa el número de arcos que deben ser recorridos en promedio
para llegar, partiendo de la raíz, a un nodo cualquiera del árbol.
• La LCIM del árbol anterior es:
LCIM = 36 / 12 = 3
ARBOLES BINARIOS
Definición
• Un árbol ordenado es aquel en el cual la distribución de las ramas
sigue cierto orden. Los árboles ordenados de grado 2 son de especial
interés puesto que representan una de las estructuras de datos más
importante en computación, conocida como árboles binarios.
• En un árbol binario cada nodo puede tener como máximo dos
subárboles; y siempre es necesario distinguir entre el subárbol
izquierdo y el subárbol derecho
Árbol Binario de Búsqueda
Representación de una Expresión Algebraica
Árbol Binario
Tipos de Arboles
Tipos de Arboles
Los arboles pueden clasificarse tomando en cuenta su estructura y
funcionamiento. A continuación, se presentan los tipos de árboles más
utilizados (Cairó & Guardati, 2006):
Arboles binarios.
• Arboles binarios distintos
• Arboles binarios similares
• Arboles binarios equivalentes
• Arboles binarios completos
• Arboles binarios llenos
• Arboles binarios degenerados
• Arboles binarios de búsqueda
• Arboles equilibrados
Arboles multicaminos
• Arboles-B
• Arboles B+
• Arboles 2-4
Arboles Binarios
Esta estructura se caracteriza por que cada nodo solo puede tener
máximo 2 hijos, dicho de otra manera, es un árbol grado dos.
Árboles binarios distintos, similares y
equivalentes
• Árboles binarios distintos. Dos árboles binarios son distintos cuando sus
estructuras son diferentes.
• Árboles binarios similares. Dos árboles binarios son similares cuando sus
estructuras son idénticas, pero la información que contienen sus nodos difiere
entre sí.
• Árboles binarios equivalentes. Los árboles binarios equivalentes se definen como
aquellos que son similares y además los nodos contienen la misma información.
Arboles distintos
Arboles similares
A
B
A
C
D
B
C
A
B
D
A
P
C
D
Arboles equivalentes
Q
R
S
B
A
C
D
B
C
D
Árboles binarios completos
• Un árbol binario completo de profundidad n es un árbol en el que,
para cada nivel, del 0 al nivel n-1 tiene un conjunto lleno de nodos y
todos los nodos hoja a nivel n ocupan las posiciones más a la
izquierda del árbol
Árbol binario completo
Árbol binario completo
A
B
Árbol binario completo
A
A
B
C
D
Árbol binario NO
completo
Facultad de
B
A
C
D
tica
E
F
Árbol binario NO
completo
A
B
C
E
D
Árbol binario NO
completo
A
B
C
C
B
F
rm tica
E
F
Árboles binarios llenos
• Es un árbol lleno donde todos los nodos tienen cero o dos hijos. Es
decir, no existe un nodo que tenga un solo hijo.
Árbol binario lleno
Árbol binario lleno
A
B
Árbol binario lleno
A
B
C
D
Árbol binario NO lleno
A
C
E
E
D
A
A
B
B
E
C
B
C
D
G
F
Árbol binario NO lleno
Árbol binario NO lleno
A
C
B
F
Facultad de Estadístic a Informátic
e
a
D
E
F
Árboles binarios degenerados
• Es un tipo especial denominado árbol degenerado en el que hay un
solo nodo hoja y cada nodo no hoja sólo tiene un hijo. Un árbol
degenerado es equivalente a una lista enlazada.
Lista enlazada
Árbol binario degenerado
A
A
BB
C
D
E
B
C
D
E
Árboles binarios equilibrados
• Cuando un árbol binario de búsqueda crece descontroladamente hacia un
extremo su rendimiento puede disminuir considerablemente. Para mantener la
eficiencia de operación surgen los árboles equilibrados o balanceados. Estos
pueden realizar acomodos o balanceos después de inserciones o eliminaciones
de elementos.
Árbol binario no equilibrado
Árbol binario equilibrado AVL
15
15
12
12
18
30
29
10
7
13
Árbol binario perfectamente equilibrado
15
12
0
2
18 22
11
Facultad de Estadística e Informática
10
13
0
2
18 22
Arboles binarios perfectamente equilibrados
Un árbol perfectamente equilibrado es un árbol binario en el que, para
todo nodo, el número de nodos en el subárbol izquierdo y el número
de nodos en el subárbol derecho difieren como mucho en una unidad.
Árbol binario no equilibrado
Árbol binario equilibrado AVL
15
15
12
12
18
30
29
10
7
13
Árbol binario perfectamente equilibrado
15
12
0
2
18 22
11
Facultad de Estadística e Informática
10
13
0
2
18 22
Arboles binarios equilibrados AVL
• Un árbol equilibrado en sentido AVL (Adelson-Velskii y Landis, 1962)
es un árbol binario en el que la diferencia de alturas de los subárboles
izquierdo y derecho correspondientes a cualquier nodo del árbol no
es superior a uno.
Árbol binario no equilibrado
Árbol binario equilibrado AVL
15
15
12
12
18
30
29
10
7
13
Árbol binario perfectamente equilibrado
15
12
0
2
18 22
11
Facultad de Estadística e Informática
10
13
0
2
18 22
Arboles multicaminos
• Un árbol multicaminos es una estructura de datos homogénea, dinámica y no
lineal, en donde a cada nodo le pueden seguir una cantidad n de nodos hijos...
• Mientras que los árboles binarios fueron pensados para trabajar en memoria
principal, los arboles multicaminos fueron diseñados para trabajar con sistemas
de archivos (Serrano Montero, 2006).
Árbol multicaminos
15
12
30
29
04
18
36
31
37
56
58
Árboles binarios de búsqueda
Árboles binarios de búsqueda
Un árbol binario que tiene los nodos
ordenados de alguna manera se conoce
como árbol binario de búsqueda.
Se puede buscar aplicando el criterio de
búsqueda binaria similar al utilizado con
arreglos.
En concreto, un árbol binario de búsqueda es
aquel en que, dado un nodo, todos los datos
del subárbol izquierdo son menores que los
datos de ese nodo, mientras que todos los
datos del subárbol derecho son mayores que
el nodo.
Árbol binario de búsqueda
55
30
41
4
2
5
75
7
85
Árboles binarios de búsqueda
Formalmente se define un árbol binario de
búsqueda de la siguiente manera (Cairó &
Guardati, 2006):
• Para todo nodo T del árbol se debe cumplir
que todos los valores almacenados en el
subárbol izquierdo de T sean menores a la
información guardada en el nodo T. De
forma similar, todos los valores
almacenados en el subárbol derecho de T
deben ser mayores a la información
guardada en el nodo T.
Árbol binario de búsqueda
55
30
41
4
2
5
757
85
Ventajas de los
árboles binarios
de búsqueda
En un arreglo es posible localizar datos
eficientemente si estos se encuentran
ordenados, pero las operaciones de inserción y
eliminación resultan costosas, porque
involucran movimiento de los elementos
dentro del arreglo.
En las listas, por otra parte, dichas operaciones
se pueden llevar a cabo con facilidad, pero la
operación de búsqueda, en este caso, es una
operación que demanda recursos, pudiendo
inclusive requerir recorrer todos los elementos
de ella para llegar a uno en particular.
Creación de un árbol binario de búsqueda
• Graficar un árbol binario con los siguientes datos:
9, 2, 1, 16, 6, 11, 8, 4
9
9
Árboles binarios de búsqueda Implementación
El nodo raíz (nodo B) es el primer nodo en un árbol. Cada enlace en el
nodo raíz hace referencia a un hijo (nodos A y D). El hijo izquierdo
(nodo A) es el nodo raíz del subárbol izquierdo (que sólo contiene el
nodo A), y el hijo derecho (nodo D) es el nodo raíz del subárbol
derecho (que contiene los nodos D y C).
Árboles binarios de búsqueda
Implementación
esVacio()
Constructor
Destructor
[1] Insertar elemento
[2] Mostrar árbol completo acostado con la raíz a la izquierda
[3] Graficar árbol completo
[4] Buscar un elemento en el árbol
[5] Recorrer el árbol en PreOrden
[6] Recorrer el árbol en InOrden
[7] Recorrer el árbol en PostOrden
[8] Eliminar un nodo del árbol PREDECESOR
[9] Eliminar un nodo del árbol SUCESOR
[10] Recorrer el árbol por niveles (Amplitud)
[11] Altura del árbol
[12] Cantidad de hojas del árbol
[13] Cantidad de nodos del árbol
[15] Revisa si es un árbol binario completo
[16] Revisa si es un árbol binario lleno
[17] Eliminar el árbol
Árboles binarios de búsqueda.
Implementación
• La Clase Nodo
• Crea un Nodo formado por los campos
• Dato (de tipo entero) corresponde al valor
que contiene el nodo
• Nodo*izquierdoPtr
• Nodo*derechoPtr
izq
dato
der
Árboles binarios de
búsqueda.
Implementación
• Clase Árbol
• Crea un Nodo raíz del árbol
raizPtr
Árboles binarios de búsqueda.
Implementación
o Método Constructor Arbol::Arbol()
o Inicializa la raíz del Árbol con valor Nulo.
raizPtr
NULL
Árboles binarios de búsqueda.
Implementación
o Método Destructor Arbol::~Arbol()
o Libera la memoria ocupada por los nodos del
árbol.
o Emplea el método Arbol::podarArbol(Nodo
*&nodoPtr)
Árboles binarios de búsqueda.
Implementación
o Método Arbol::esVacio()
o Verifica si la raíz del árbol apunta a
vacío.
Árboles binarios de búsqueda.
Implementación
o Método Nodo *Arbol::regresaRaiz()
o Regresa el nodo de la raíz del árbol.
Árboles binarios de búsqueda.
Implementación
o Método void Arbol::insertarNodo(int
valor, Nodo *&nodoPtr)
o Crea un nuevo nodo y lo inserta en el lugar
correspondiente dentro del árbol.
Árboles binarios de búsqueda.
Implementación
o Método void Arbol::insertarNodo(int
valor, Nodo *&nodoPtr)
o Valor=4
Facultad de Estadística e Inf
Llamada a Arbol::insertarNodo en el menú principal,
donde podemos observar los parámetros que se le
envían:
raizPtr
Árboles binarios de búsqueda.
Implementación
o Método void Arbol::insertarNodo(int
valor, Nodo *&nodoPtr)
o Valor=4
izquieroPtr
dato
derechoPtr
8
3
20
1
NULL
NULL
NULL
NULL
10
5
NULL
NULL
7
NULL
NULL
Primera iteración de la recursión:
nodoPtr = raizPtr (nodoPtr no es nulo)
4<8
insertarNodo (4, nodoPtr→izquierdoPtr)
Se llama nuevamente el método insertar Nodo con
el valor 4 a insertar y la dirección del nodo que
contiene el número 3 (a la izquierda del 8).
raizPtr
Árboles binarios de búsqueda.
Implementación
o Método void Arbol::insertarNodo(int
valor, Nodo *&nodoPtr)
o Valor=4
izquieroPtr
dato
derechoPtr
8
3
20
1
NULL
NULL
NULL
NULL
10
5
NULL
NULL
7
NULL
NULL
Segunda iteración de la recursión:
nodoPtr = nodo con el dato 3 (nodoPtr no es nulo)
4>3
insertarNodo (4, nodoPtr→derechoPtr)
Se llama nuevamente el método insertar Nodo con
el valor 4 a insertar y la dirección del nodo que
contiene el número 5 (a la derecha del 3).
raizPtr
Árboles binarios de búsqueda.
Implementación
o Método void Arbol::insertarNodo(int
valor, Nodo *&nodoPtr)
o Valor=4
izquieroPtr
dato
derechoPtr
8
3
20
1
NULL
NULL
NULL
NULL
10
5
NULL
NULL
7
NULL
NULL
Tercera iteración de la recursión:
nodoPtr = nodo con el dato 5 (nodoPtr no es nulo)
4<5
insertarNodo (4, nodoPtr→izquierdoPtr)
Se llama nuevamente el método insertar Nodo con
el valor 4 a insertar y la dirección del nodo a la
izquierda de 5, es decir NULL.
raizPtr
Árboles binarios de búsqueda.
Implementación
o Método void Arbol::insertarNodo(int
valor, Nodo *&nodoPtr)
o Valor=4
izquieroPtr
dato
derechoPtr
8
3
20
1
NULL
NULL
NULL
NULL
10
5
NULL
NULL
7
NULL
NULL
Cuarta iteración de la recursión:
nodoPtr = NULL
Por lo tanto ingresa al if (nodoPtr==NULL) y crea un
nuevo nodoPtr:
4
NULL
NULL
raizPtr
Árboles binarios de búsqueda.
Implementación
o Método void Arbol::insertarNodo(int
valor, Nodo *&nodoPtr)
o Valor=4
izquieroPtr
dato
derechoPtr
8
3
NULL
NULL
NULL
7
4
NULL
NULL
10
5
1
NULL
20
NULL NULL
NULL
Cuarta iteración de la recursión:
nodoPtr contiene el nuevo nodo creado a la izquierda
del nodo con el dato 5.
Árboles binarios de búsqueda.
Implementación
o Método Arbol::muestraAcostado(int
nivel, Nodo *nodoPtr)
20
10
raizPtr
8
7
o Escribe en pantalla el árbol en forma
horizontal, con la raíz a la izquierda.
5
4
3
1
Árboles binarios de búsqueda.
Implementación
o Método Arbol::muestraAcostado(int
nivel, Nodo *nodoPtr)
o Escribe en pantalla el árbol en forma
horizontal, con la raíz a la izquierda.
Árboles binarios de búsqueda.
Implementación
o Método Arbol::muestraAcostado(int
nivel, Nodo *nodoPtr)
Llamada a Arbol::muestraAcostado en el menú
principal, donde podemos observar los parámetros
que se le envían:
Recorrido en InOrden
(izquierdo, raíz, derecho). El valor en un nodo no se procesa hasta que se procesen los valores en
su subárbol izquierdo.
Para recorrer un árbol binario no vacío en InOrden, hay que realizar las siguientes operaciones
recursivamente en cada nodo, comenzando con el nodo raíz:
Recorrer el subárbol izquierdo InOrden
Procesa la raíz
Recorrer el subárbol derecho InOrden
imprime los valores en orden ascendente.
Secuencia: 6 – 13 – 17 – 27 – 33 – 42 - 48
Recorrido en InOrden
(izquierdo, raíz, derecho). El valor en un nodo no se procesa hasta que se procesen los valores en
su subárbol izquierdo.
Para recorrer un árbol binario no vacío en InOrden, hay que realizar las siguientes operaciones
recursivamente en cada nodo, comenzando con el nodo raíz:
8
Recorrer el subárbol izquierdo InOrden
Procesa la raíz
3
0
2
5
1
10
Recorrer el subárbol derecho InOrden
4
imprime los valores del nodo en orden ascendente.
7
Secuencia: 1 – 3 – 4 – 5 – 7 – 8 – 10 – 20
Recorrido en InOrden
(izquierdo, raíz, derecho)
Llamada en main:
Recorrido en PreOrden
(raíz, izquierdo, derecho). Para recorrer un árbol binario no vacío en
PreOrden, hay que realizar las siguientes operaciones recursivamente
en cada nodo, comenzando con el nodo raíz:
Procesa la raíz
Recorrer el subárbol izquierdo en PreOrden
Recorrer el subárbol derecho en PreOrdenda
Secuencia: 27 – 13 – 6 – 17 – 42 – 33 - 48
Recorrido en PreOrden
Recorrido en PreOrden
(raíz, izquierdo, derecho)
Recorrido en PostOrden
(izquierdo, derecho, raíz). Para recorrer un árbol binario no vacío en
PostOrden, hay que realizar las siguientes operaciones recursivamente
en cada nodo, comenzando con el nodo raíz:
Recorrer el subárbol izquierdo en PostOrden
Recorrer el subárbol derecho en PostOrden
Procesa la raíz
Recorrido en PostOrden
Recorrido en PostOrden
(izquierdo, derecho, raíz)
Árboles binarios de búsqueda.
Implementación
• Escribe la secuencia de elementos del siguiente árbol recorriéndolo
en: inOrden, preOrden y postOrden.
Solución:
InOrden: 7, 9, 10, 12, 15, 25, 30, 35.
PreOrden: 12, 9, 7, 10, 25, 15, 30, 35.
PostOrden: 7, 10, 9, 15, 35, 30, 2
Árboles binarios de búsqueda.
Implementación
• Recorrido en PostOrden del siguiente árbol:
Árboles binarios de búsqueda.
Implementación
o Método Arbol::busqueda(int x, Nodo *nodoPtr).
o Es el método para buscar un valor x de manera recursiva, en el campo dato de los
nodos de un árbol.
Árboles binarios de búsqueda.
Implementación
o Con valores iniciales se tienen el valor a buscar y la raíz del arbol :
Árboles binarios de búsqueda.
Implementación
o Actividad:
o Por lo tanto:
1. nodoPtr toma como valor inicial, al ingresar al método, la raíz del árbol. Si el
valor de x es mayor a la raíz, se realiza el paso recursivo con el lado derecho. Si
el valor de x es menor se realiza el paso recursivo con el lado izquierdo.
2. Si x no es mayor ni menor, significa que se ha encontrado el nodo con el valor
de x y regresará True.
3. Si se llegó a un nodo Nulo, se retorna False.
Árboles binarios de búsqueda.
Implementación
o Método Arbol::busqueda(int x,
Nodo *nodoPtr)
o Busca el valor de “x” en los nodos del
árbol.
Árboles binarios de búsqueda.
Implementación
o void Arbol::podarArbol(Nodo
*&nodoPtr)
o Libera memoria de los nodos
del árbol.
Arboles AVL
Problema de los árboles binarios de búsqueda
• Los
árboles binarios, son eficientes en las operaciones de búsqueda, inserción y eliminación
cuando el árbol crece o decrece descontroladamente, la eficiencia de la estructura de datos decae.
Insertar los datos
15,18,30,60
Insertar los datos
32,11,9,4,
Se expanden
incrementando las
comparaciones,
operación de O(N)
15
18
Mas Critico cuando el
árbol crece
ordenadamente
30
32
11
9
60
4
Variantes de los árboles binarios de búsqueda
• Con el objetivo de mantener la eficiencia en la operación de
búsqueda surgen modificaciones a las reglas de operación del árbol
binario de búsqueda.
• Surge el Árbol Balanceado (AVL)
• Estas variantes presentan ventajas en cuanto al rendimiento que
ofrecen a la hora de realizar búsquedas principalmente.
Árbol balanceado AVL
• La principal característica de estos es la de realizar reacomodos o
balanceos, después de inserciones o eliminaciones de elementos.
• Estos árboles también reciben el nombre de AVL (autores: 2
matemáticos rusos G.M. Adelson-Velskii y E.M Landis en 1962).
• Formalmente se define un árbol balanceado como un árbol de
búsqueda, en el cual se debe cumplir la siguiente condición: “Para
todo nodo T del árbol la altura de los subárboles izquierdo y
derecho no deben diferir en a lo sumo una unidad”.
Definición
• Básicamente un árbol AVL es un Árbol Binario de Búsqueda al que se
le añade una condición de equilibrio.
“Para todo nodo la altura de sus subárboles izquierdo y
derecho pueden diferir a lo sumo en 1”.
• Gracias a esta forma de equilibrio (o balanceo), la complejidad de una
búsqueda en uno de estos árboles se mantiene siempre en orden de
complejidad O(log n).
Condición de equilibrio
“Para todos los nodos, la altura de la rama izquierda no
difiere en mas de una unidad de la altura de la rama
derecha”
Características
• Un AVL es un ABB.
• La diferencia entre las alturas de los subárboles. derecho e
izquierdo no debe excederse en más de 1.
• Cada nodo tiene asignado un peso de acuerdo a las alturas
de sus subárboles.
• Un nodo tiene un peso de 1 si su subárbol derecho es más
alto, -1 si su subárbol izquierdo es más alto y 0 si las alturas
son las mismas.
Equilibrio
Factor Equilibrio = (altura derecha )– (altura izquierda)
Describe relatividad entre subárbol derecho y subárbol izquierdo.
• + (positivo) → derecha mas alto (profundo)
• - (negativo) → izquierda mas alto (profundo)
“Un árbol binario es un AVL si y sólo si cada uno de sus nodos tiene un
equilibrio de –1, 0, + 1”
• Si alguno de los pesos de los nodos se modifica en un valor no válido
(2 ó -2) debe seguirse un esquema de rotación.
Desequilibrios
• Desequilibrio hacia la
izquierda (Equilibrio > +1)
• Desequilibrio hacia la derecha
(Equilibrio < -1)
Operaciones sobre un AVL
1. Inserta nodo
2. Balancear
• Rotación Simple a la Derecha (RSD): Se tiene un factor de equilibrio de -2 y su nodo
izquierdo no tiene un factor de equilibrio de 1.
• Rotación Simple a la Izquierda (RSI): Se tiene un factor de equilibrio de 2 y su nodo
derecho no tiene un factor de equilibrio de -1.
• Rotación Doble a la Izquierda (RDI): Se tiene un factor de equilibrio de 2 y su nodo
derecho tiene un factor de equilibrio de -1.
• Rotación Doble a la Derecha (RDD): Se tiene un factor de equilibrio de -2 y su nodo
izquierdo tiene un factor de equilibrio de 1.
3. Eliminar todo
4. Calcular altura
Insertar un nodo
1. Se usa la misma técnica que para insertar un nodo en un ABB
ordenado
2. Trazamos una ruta desde el nodo raíz hasta un nodo hoja (donde
hacemos la inserción).
3. Insertamos el nodo
4. Volvemos a trazar la ruta de regreso al nodo raíz, ajustando el
equilibrio a lo largo de ella. nuevo.
5. Si el equilibrio de un nodo llega a ser + - 2, volvemos a ajustar los
subárboles de los nodos para que su equilibrio se mantenga acorde
con los lineamientos AVL (que son +- 1)
Balancear
• Caso 1: Rotación simple izquierda RSI: Si esta desequilibrado a la
izquierda (E>+1) y su hijo derecho tiene el mismo signo (+) hacemos
rotación sencilla izquierda.
• Caso 2: Rotación simple derecha RSD: Si esta desequilibrado a la
derecha (E<-1) y su hijo izquierdo tiene el mismo signo (-) hacemos
rotación sencilla derecha.
• Caso 2: Rotación simple derecha RSD
-1
0
D
D
Rotación simple izquierda o derecha.
Observaciones:
• Se conserva el orden apropiado del árbol.
• Restablece todos los nodo a equilibrios apropiados AVL
• Conserva el recorrido en orden que el árbol anterior.
• Sólo se necesita a lo más modificar 3 apuntadores para lograr el
nuevo equilibrio (con la de la raíz)
• Caso 3: Rotación doble izquierda RDI: Si está desequilibrado a la
derecha (E< –1), y su hijo izquierdo tiene distinto signo (+) hacemos
rotación doble izquierda-derecha.
• Caso 3: Rotación doble izquierda RDI
• Caso 4: Rotación doble derecha RDD: Si esta desequilibrado a la
izquierda (E>+1), y su hijo derecho tiene distinto signo (–) hacemos
rotación doble derecha-izquierda.
• Caso 4: Rotación doble derecha RDD
Eliminar
• Al eliminar un nodo en un árbol AVL puede afectar el equilibrio de sus
nodos. Entonces hay que hacer rotaciones simples o dobles.
• Eliminar un nodo se realiza de la misma manera que en un árbol
binario ordenado. Al localizar el nodo que se desea eliminar se realiza
el siguiente procedimiento:
• Si el nodo es un nodo hoja, simplemente lo eliminamos.
• Si el nodo solo tiene un hijo, lo sustituimos con su hijo.
• Si el nodo eliminado tiene dos hijos, lo sustituimos por el nodo que se
encuentra mas a la derecha en el subárbol izquierdo o más a la izquierda en el
subárbol derecho.
Una vez que se ha eliminado el nodo, se tiene que equilibrar el árbol:
• Si el equilibrio del padre del nodo eliminado cambia de 0 a +-1 el algoritmo
concluye.
• Si el padre del nodo eliminado cambio de +-1 a 0, la altura del árbol ha
cambiado y se afecta el equilibrio de su abuelo.
• Si el equilibrio del padre del nodo eliminado cambia de +- 1 a +- 2 hay que
hacer una rotación. Después de concluirla, el equilibrio del padre podría
cambiar, lo que, a su vez, podría forzarnos a hacer otros cambios (y
probables rotaciones) en toda la ruta hacia arriba a medida que
ascendemos hacia la raíz. Si encontramos en la ruta un nodo que cambie
de 0 a +- 1 entonces se concluye.
Inserción
• Ejemplos de Rotación
Simple
• Rotaciones Dobles
Eliminar
• Eliminar (32)
Complejidad de búsqueda
• Los árboles AVL están siempre equilibrados de tal modo que para
todos los nodos, la altura de la rama izquierda no difiere en mas de
una unidad de la altura de la rama derecha. Gracias a esta forma de
equilibrio (o balanceo), la complejidad de una búsqueda en uno de
estos arboles se mantiene siempre en orden de complejidad O(log2n).
Orden de complejidad
O(f(n))
N=100
N=200
En un t=2h
(N=?)
log n
1h
1.15 h
10000
n
1h
2h
200
n log n
1h
2.30 h
199
n2
1h
4h
141
n3
1h
8h
126
2n
1h
1030 h
101
Arboles B+
Definición
• Los árboles B+ son una variante de los árboles B,
se diferencian en que los arboles B+ toda la información se
encuentra almacenada en las hojas. En la raíz y en las páginas
internas se encuentran almacenado índices o claves para
llegar a un dato.
Características de los árboles B+
• La raíz almacena como mínimo un dato y como máximo m-1
datos.
• La página raíz tiene como mínimo dos descendientes.
• Las páginas intermedias tienen como mínimo (m-1)/2(Parte
entera) datos.
• Las páginas intermedias tienen como máximo m-1 datos.
• Todas las paginas hojas tienen la misma altura
• La informacion se encuentra ordenada.
• Toda la informacion se encuentra almacenada en las páginas
hoja, por lo que en las páginas internas se puede duplicar las
claves.
Ejemplo
• Ejemplo de un árbol B+ de orden 5:
Inserción en un árbol B+:
1. Se ubica en la página raíz.
2. Se evalúa si es una página hoja.
• Si la respuesta es afirmativa, se evalúa si no sobrepasa los limites de
datos.
• Si la respuesta es afirmativa, entonces se procede a insertar el nuevo valor en
lugar del correspondiente.
• Si la respuesta es negativa, se divide la página en dos, se sube una copia de la
mediana a la página padre, si la página padre se encuentra llena se debe de
partir igual y así el mismo proceso hasta donde sea necesario, si este proceso
llega hasta la raíz la altura del árbol aumenta en uno.
• Si no es hoja, se compara el elemento a insertar con cada uno de los
valores almacenados para encontrar la página descendiente donde
proseguir la búsqueda. Se regresa al paso 1.
Ejemplo
• Insertar las siguientes claves a un árbol de orden 5: 10-27-29-17-2521-15-31-13-51-20-24-48-19-60-35-66
Eliminación
La operación de eliminación en árboles-B+ es más simple que
en árboles-B. Esto ocurre porque las claves a eliminar siempre
se encuentran en las páginas hojas. En general deben
distinguirse los siguientes casos:
1.Si al eliminar una clave, la cantidad de llaves queda mayor o
igual que [m/2] entonces termina la operación. Las claves de
los nodos raíz o internos no se modifican por más que sean
una copia de la clave eliminada en las hojas.
2.Si al eliminar una clave, la cantidad de llaves queda menor que
[m/2] entonces debe realizarse una redistribución de claves,
tanto en el índice como en las paginas hojas.
Arboles Rojos - Negros
Definición
Un árbol rojo-negro es un árbol binario de búsqueda equilibrado, una
estructura de datos utilizada en informática y ciencias de la
computación. La estructura original fue creada por Rudolf Bayer en
1972, que le dio el nombre de “árboles-B binarios simétricos”, pero
tomó su nombre moderno en un trabajo deLeo J. Guibas y Robert
Sedgewick realizado en 1978. Es complejo, pero tiene un buen peor
caso de tiempo de ejecución para sus operaciones y es eficiente en la
práctica. Puede buscar, insertar y borrar en un tiempo O(log n), donde
n es el número de elementos del árbol
Eficiencia
1. En primer lugar, el árbol rojo-negro no cumple la condición de equilibrio del
árbol AVL, es decir, el árbol de búsqueda binario en el que la altura de los
subárboles izquierdo y derecho de cada nodo es como máximo 1 diferente. Sin
embargo, se propone agregar color al nodo. El árbol rojo-negro es usar un
equilibrio no estricto para reducir el número de rotaciones al agregar y eliminar
nodos. Cualquier desequilibrio se resolverá en tres rotaciones, y AVL es un
árbol estrictamente equilibrado, por lo que se agrega o elimina. En el momento
del nodo, según diferentes situaciones, el número de rotaciones es mayor que
el del árbol rojo-negro. Entonces la eficiencia de inserción del árbol rojo-negro
es mayor
2. El árbol rojo-negro puede buscar, insertar y eliminar operaciones con
complejidad de tiempo O (log2 (n))
3. En términos simples, el árbol rojo-negro es para resolver los defectos del árbol
de búsqueda binario, porque el árbol de búsqueda binario se degenerará en
una estructura lineal en algunos casos.
Comparación y selección de árboles rojonegros y árboles equilibrados.
1. La estructura de árbol equilibrada es más intuitiva y el rendimiento
de lectura es mayor que el del árbol rojo-negro; el rendimiento de
agregar y eliminar nodos para restaurar el equilibrio no es tan
bueno como el árbol rojo-negro
2. Árboles rojo-negros, el rendimiento de lectura no es tan bueno
como el de los árboles balanceados; agregar y eliminar nodos
restaura el rendimiento balanceado mejor que los árboles
balanceados
Claves duplicadas
en un árbol de búsqueda, las claves duplicas no representan ningún
problema y por tanto son permitidas.
En un arbol rojo negro, las claves duplicadas representan un problema
al momento de insertar/eliminar nodos. Por lo tanto, en un árbol rojo
negro no permitimos la existencia de claves duplicadas.
Propiedades de arboles rojos negros
Los colores son utilizados para acotar las estructuras permitidas. En
particular, en un árbol rojo negro el camino mas largo puede ser a lo sumo 2
veces mas largo que el camino mas corto.
Las propiedades que definen a los arboles rojo y negro son:
1. Cada nodo es negro o rojo.
2. El nodo raíz es negro.
3. Cada nodo hoja (NIL O NULL) es negro. (refiere a un nodo hoja que está
vacío)
4. Si un nodo es rojo, sus nodos secundarios deben ser negros.
5. Todas las rutas desde un nodo a sus descendientes contienen el mismo
número de nodos negros.
Altura negra
Definimos la altura negra de un nodo x, denotada por bh(x), como el
numero de nodos negros, sin incluir x, en un camino simple desde x
hasta las hojas.
Por la propiedad 5 la altura negra es bien definida.
Altura Negra
• Un árbol rojo negro con n claves (nodos internos) tiene altura h
menor o igual a 2 log2(n+1)