DESTREZAS 6° MATEMÁTICAS MDHERI

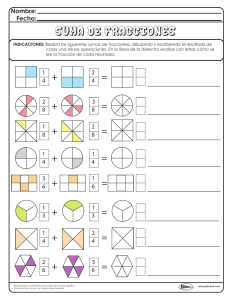
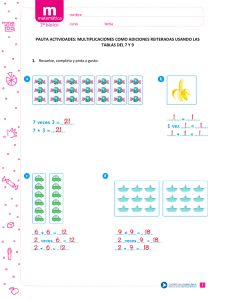
DESTREZAS
6° grado
1. Relaciona las columnas con líneas de colores.
a) Noventa y dos millones
quinientos cuarenta y ocho mil
sesenta y dos.
b) Doscientos cuarenta y tres
millones seiscientos treinta y
ocho mil ciento cuarenta y uno.
a) 300 000 000
b) 130 000 000
c) 906 420 306
c) Trescientos millones.
d) Ciento catorce millones
noventa
y
cuatro
mil
ochocientos cuatro.
e) Cuatrocientos once millones
cuatrocientos
once
mil
cuatrocientos once.
f)
Ochocientos
millones
trescientos treinta y tres mil.
g) Ciento treinta millones.
h) Quinientos setenta y cuatro
mil novecientos setenta y uno.
i) Novecientos
cuatrocientos
trescientos seis.
seis millones
veinte
mil
j) Cuatrocientos treinta millones
trescientos cuarenta y cinco mil
seiscientos setenta y ocho.
d) 92 548 062
e) 411 411 411
f)
574 971
g) 114 094 804
h) 430 345 678
i)
243 638 141
j)
800 333 000
2. Escribe con letra como se leen las siguientes cantidades.
a)
692 303 741 ________________________________________________________________
________________________________________________________________________________
b) 285 342 644 _________________________________________________________________
________________________________________________________________________________
c) 842 963 321 _________________________________________________________________
________________________________________________________________________________
d) 986 653 319__________________________________________________________________
________________________________________________________________________________
e) 524 549 889 _________________________________________________________________
________________________________________________________________________________
f) 113 659 772 __________________________________________________________________
________________________________________________________________________________
g) 637 648 074 _________________________________________________________________
_______________________________________________________________________________
3. Escribe los números con cifras.
1.
Trescientos catorce millones treinta y ocho mil diecisiete.
2.
Ochocientos
cuarenta y seis millones doscientos noventa y tres mil
setecientos cuarenta y dos.
3.
Doscientos setenta millones ciento veinticuatro mil setecientos cincuenta y
nueve.
4.
Cuatrocientos diecinueve millones doscientos treinta y seis mil setecientos.
5.
Setecientos noventa y cinco millones quinientos doce mil uno.
6.
Novecientos doce millones quinientos sesenta y ocho mil trescientos cuarenta
y siete.
7. Quinientos millones seiscientos treinta y ocho mil seiscientos treinta y ocho.
El valor posicional es el valor que representa un número de acuerdo
con la posición en la que está.
ejemplo
73 481 942 = el número 4 representa las centenas de millar, por lo que
su valor es de 400 000
73 481 942 = en este caso, el número 4 representa las decenas, por lo
que su valor es de 40
1. Marca con una  los enunciados correctos y con una X
los que sean incorrectos.
a) En el número 732 654 125 el 4 ocupa la posición de decenas de millar.
b) En el número 528 934 679 el 2 ocupa la posición de las unidades de millón.
c) En el número 687 280 347 el 4 ocupa la posición de las decenas.
d) En el número 334 857 919 el 9 ocupa la posición de unidades de millar.
e) En el número 721 092 155 el 7 ocupa la posición de centenas de millón.
f) En el número 376 480 723 el 6 ocupa la posición de unidades de millón.
g) En el número 160 521 903 el 5 ocupa la posición de centenas.
h) En el número 248 339 362 el 3 ocupa la posición de decenas de millar.
i) En el número 521 465 237 el 2 ocupa la posición de unidades de millar.
2. Circula lo que se te pide.
a)Circula el número que representa la unidad de millar
843 123 182
b)Circula el número que representa la decena de millón.
843 123 182
c) Circula el numero que representa la centena de millón.
843 123 182
d)Circula el número que representa la decena.
843 123 182
e) Circula el número que representa la unidad de millón.
843 123 182
f) Circula el número que representa la centena.
843 123 182
g)Circula el número que representa la decena de millar.
843 123 182
h) Circula el número que representa la centena de millar.
843 123 182
i) Circula el número que representa la unidad.
843 123 182
3. Escribe el valor posicional de los números marcados.
a) 742 349 754
50
300 000
_______________
y ________________
b) 864 851 997
_______________ y ________________
c) 533 651 958
_______________ y ________________
d) 783 664 229
_______________ y ________________
e) 755 422 641
_______________ y ________________
f)
844 265 745
_______________ y ________________
g) 918 736 651
_______________ y ________________
h) 246 368 147
_______________ y ________________
i)
235 674 898
_______________ y ________________
j)
554 621 865
_______________ y ________________
k) 297 364 115
_______________ y ________________
l)
992 173 119
_______________ y ________________
m) 622 291 499
_______________ y ________________
n) 384 756 104
_______________ y ________________
1. Escribe los símbolos <,> o =, según corresponda. Escribe
con letra el número mayor.
a) 134 764 329
297 541 981____________________________
___________________________________________________________
b) 244 374 123
244 347 123____________________________
___________________________________________________________
c) 864 752 662
864 752663____________________________
___________________________________________________________
d) 918 273 645
918 273 654____________________________
___________________________________________________________
e) 437 914 763
411 683 942____________________________
___________________________________________________________
f) 981 762 691
981 762 691____________________________
___________________________________________________________
g) 437 393 664
437 393 664____________________________
___________________________________________________________
h) 613 715 886
613 715 868____________________________
___________________________________________________________
2. Escribe los símbolos <,> o =, según corresponda. Escribe
con letra el número mayor.
a) 478 881 934
487 881 943____________________________
___________________________________________________________
b) 64 990 361
171 455 821____________________________
___________________________________________________________
c) 333 333 353
333 335 333____________________________
___________________________________________________________
d) 921 556 376
480 723 160____________________________
___________________________________________________________
e) 631 529 874
631 529 874____________________________
___________________________________________________________
f) 761 909 081
761 099 108____________________________
___________________________________________________________
g) 987 654 321
987 645 321____________________________
___________________________________________________________
h) 483 561 774
483 561 774____________________________
___________________________________________________________
La notación desarrollada consiste en descomponer un número en las
distintas cantidades que lo conforman.
EJEMPLO
123 456 789 = 100 000 000 + 20 000 000 + 3 000 000 + 400 000 + 50 000 +
6 000 + 700 + 80 + 9
1. Escribe
cantidades.
en
notación
desarrollada
las
siguientes
a)176 994 531 = _____________________________________________
_____________________________________________________________
b) 753 998 412 = _____________________________________________
_____________________________________________________________
c) 531 221 878 = _____________________________________________
_____________________________________________________________
d) 915 678 349 = _____________________________________________
_____________________________________________________________
e) 211 771 528 = _____________________________________________
_____________________________________________________________
f) 489 912 423 = _____________________________________________
_____________________________________________________________
g) 892 332 614 = _____________________________________________
_____________________________________________________________
2. Escribe el resultado de la notación desarrollada.
a) 300 000 000 + 80 000 000 + 4 000 000 + 500 000 + 70 000 + 1 000 + 900 + 20 + 6
b) 600 000 000 + 20 000 000 + 9 000 000 + 100 000 + 50 000 + 7 000 + 400 + 80 + 3
c) 200 000 000 + 90 000 000 + 7 000 000 + 200 000 + 50 000 + 1 000 + 600 + 40 + 3
d) 700 000 000 + 40 000 000 + 5 000 000 + 800 000 + 60 000 + 4 000 + 200 + 50 + 9
e) 900 000 000 + 30 000 000 + 1 000 000 + 800 000 + 50 000 + 6 000 + 900 + 40 + 1
f) 500 000 000 + 70 000 000 + 2 000 000 + 400 000 + 90 000 + 3 000 + 800 + 70 + 6
g) 200 000 000 + 40 000 000 + 6 000 000 + 800 000 + 10 000 + 3 000 + 500 + 70
h) 500 000 000 + 30 000 000 + 8 000 000 + 600 000 + 10 000 + 2 000 + 400 + 50 + 8
i) 400 000 000 + 20 000 000 + 6 000 000 + 800 000 + 90 000 + 1 000 + 800 + 50 + 4
j) 900 000 000 + 10 000 000 + 8 000 000 + 200 000 + 70 000 + 3 000 + 600 + 40 + 5
3. Circula el valor que corresponde de acuerdo con el
número marcado.
1. 853 704 713
4 000 000
400 000
40 000
4 000
2. 940 812 711
10 000
1 000
100
10
3. 230 182 336
30 000
000
3 000 000
300 000
30 000
4. 722 402 488
700 000
000
70 000
000
7 000 000
700 000
5. 191 047 125
400 000
40 000
4 000
400
6. 400 800 317
3 000
300
30
3
7. 559 743 168
700 000
000
70 000
000
7 000 000
700 000
8. 397 456 719
9 000
900
90
9
9. 683 001 674
100 000
10 000
1 000
100
10. 949 751 313
50 000
000
5 000 000
500 000
50 000
11. 232 212 265
5 000
500
50
5
100 000
10 000
1 000
3 000 000
300 000
30 000
12. 141 131 924 1 000 000
13. 137 515 228
30 000
000
El redondeo es un proceso en el cual se eliminan cifras de un número
a partir de su representación decimal.
ejemplo = 127.983 = 127.98
si el siguiente decimal es mayor o igual a 5, el anterior se incrementa
en una unidad.
ejemplo = 127.987 = 127.99
1. Redondea las siguientes cantidades a dos decimales.
Observa el ejemplo.
413.27
a) 413.273 =___________________
b) 722.931 = ___________________
c) 105.208 = ___________________
d) 315.074 = ___________________
e) 807.945 = ___________________
f) 923.723 = ___________________
g) 746.011 = ___________________
h) 842.387 = ___________________
i) 461.770 = ___________________
j) 226.644 = ___________________
2. Completa la tabla. Observa el ejemplo.
4 680
5 345
7 480
5 620
4 240
3 325
8 350
2 687
6 680
4 680
4700
5 000
1
5
10
50
100
500
1 000
I
V
X
L
C
D
M
Sólo las cifras I, X Y C pueden escribirse seguidas, pero no se pueden repetir más
de tres veces.
II = 2
XXX = 30
CC= 200
La cifra escrita a la derecha de otra de mayor valor suma a ésta.
XI = 21
LV = 55
DC = 600
Toda cifra escrita a la izquierda de otra de mayor valor, se resta de ésta.
IX = 9
XL = 40
XIV = 14
Una rayita sobre un signo o varios, multiplica su valor por mil.
C = 100 000
M = 1 000 000
1. Escribe con números romanos las siguientes cantidades.
a) 9 ____________________
a) 99 ____________________
b) 300 __________________
b) 409 ___________________
c) 45 ___________________
c) 140 ___________________
d) 71 ___________________
d) 19 ____________________
e) 213 __________________
e) 806 ___________________
f) 1 001 ________________
f) 499 ___________________
g) 824 __________________
g) 244 ___________________
h) 330 __________________
h) 756 ___________________
i) 65 ___________________
i) 379 ___________________
j) 32 ___________________
j) 79 ____________________
Para escribir una cantidad superior a 1 000, se utiliza una raya.
Ejemplo: 5 560
=
V DLX
La raya significa que se multiplicó por 1 000.
1. Escribe con números arábigos.
a) VII DCI __________________
b) LXXV ___________________
c) X CDIX _________________
d) DVII ____________________
e) CCC DCCII _____________
e) XIX LXXIV _______________
f) MMMXCVIII _____________
g) IV CMLXXVII ____________
h) XXIX ____________________
i) DCC LVIV _______________
SUMAS
32.456
129.69
+ 1254.4074
3.2
1419.7534
Las partes de la suma o
adición son: los sumandos
y la suma o total.
Sumandos
Suma o total
Todos los puntos decimales al parejo.
3 125.117
+
847.332
475.25
+
317.49
624.81
+ 319.372
456 228.492
+
13 171.562
132 554.919
+
772 417.828
+
+
72.44
85.63
651 771.883
+
451 292.785
+
+
137.25
448.60
32 174.685
59 943.372
341 704.087
656 600.325
178.662
+ 921.42
+
317 481.970
80 745.741
2. Escribe las sumas en forma vertical, resuélvelas y anota los
resultados.
1.
251.77 + 523.8 =
7. 62.515 + 35.617 =
2.
31.8123 + 9.71 =
8. 265.377 + 463.884 =
3.
17.24 + 85.3157 =
9. 67.8123 + 125.63 =
4.
469.013 + 19.21 =
10. 94.36 + 17.42 =
5.
1 528.20 + 421.361 =
11. 347.82 + 514.613 =
6.
325.129 + 646.780 =
12. 1 444.008 + 6 971.358
SUMAS
Resuelve las sumas.
147 530
+ 502 486
297 059
472 116
57 309
2 482.5
+
671.26
28.79
40 231.6
+ 64 307.4
208.8
32.7
345.764
54.063
+
3.85
.914
136 209
+ 260 078
324 137
288 921
1.9999
+ 54.6237
6.8053
.1214
62 532
+ 37 208
80 695
43 624
806.267
+ 252.049
47.073
3.924
647.594
+ 810.618
422.067
631.348
Resuelve las sumas.
SUMAS
339 604 129
+ 420 178 201
180 426 532
640 129 007
+ 3 056 209
627 798
157 203 465
+ 232 007 001
465 992 677
302 584 562
+ 29 570 834
5 307 989
602 381 469
+ 149 728 577
30 276 654
183 057 164
+ 270 634 975
160 308 007
237 006 249
+ 100 267 985
523 644 386
207 376 048
+ 156 470 653
218 654 483
Resuelve las sumas.
+
9 743.221
3 465.645
343.680
174 683.521
+ 633 327.982
42 888.344
SUMAS
812 459.380
+ 839 035.612
95 321.714
654 392.881
+ 871 640.310
55 312.414
164 849.302
920 493.930
+
31 777.233
443 728.240
+ 612 333.612
735 111.819
832 847.613
+ 914 455.724
533 247.811
362 640.825
+ 31 310.633
407 700.821
647 620.322
+ 35 771.231
813 448.733
335 661.741
+ 821 127.561
707 335.480
419 632.285
+ 880 347.731
672 258.362
356 411.783
+ 412 729.666
28 158.311
SUMAS
Revisa las sumas. Marca con una
incorrectas.
957 314.207
172 516.342
1 129 830.549
+
12.7569
+ 6.3502
19.1071
+
362 477.819
174 780.327
546 258.146
174.125
+ 863.446
1 037.571
+
las correctas y con un X las
831 753.220
25 866.325
857 619.545
130.127
+ 214.444
344.571
+
250 344.710
371 417.642
621 762.352
613 017.741
+
250 340.681
873 358.422
115 862.313
+
279 911.416
395 874.729
782.2566
+ 550.3721
1 332.5287
117 888.542
+
619 328.214
737 216.546
825.1171
+611.0525
1 436.1696
Resuelve las sumas.
23 242 155
+ 345 586 402
56 101 282
364 436 354
+ 706 123 146
540 306 352
SUMAS
803 133 225
+ 203 209 195
902 361 334
126 425 235
+ 283 290 456
352 133 302
34 721 386
+ 67 156 294
86 109 142
189 352 438
+ 381 144 003
276 288 930
272 256 039
+ 269 386 382
356 364 719
34 236 275
+ 38 255 233
92 142 467
294 403 327
+ 302 903 039
639 190 465
Restas
Las partes de la resta o
sustracción
son:
el
minuendo, el sustraendo y
la resta o diferencia.
- 53850.3492
9178.5674
44671.7818
Todos los puntos decimales al parejo.
- 631 558.344
325 633.817
-
-
471 666.991
29 135.788
525 313.133
28 492.552
-
-
Minuendo
Sustraendo
Resta o
diferencia
174 161.880
61 745.621
- 259 959.384
138 742.633
253 552.873
78 324.816
619 543.349
579 321.664
-
843 843.612
525 312.927
-
932 517.725
18 335.125
325 369.537
182 643.925
-
875 321.662
617 844.333
-
472 313.819
258 313.914
Resuelve las restas.
RESTAS
- 803 304
405 822
- 423 294
192 059
- 926 943
855 752
- 176 832
159 423
- 384 362
343 853
- 625 623
300 629
- 256 632
173 981
- 713 812
625 315
- 453.883
172.721
- 683.25
517.34
-
67.93
419.36
RESTAS
Resuelve las restas.
- 328.72
155.61
- 687.33
392.65
- 789.21
605.45
- 972.622
754.32
- 1 742.8
631.62
- 377.52
245.39
- 741.33
521.78
- 888.88
325.73
- 612.93
419.36
- 453.883
172.721
- 683.25
517.34
- 67.35
32.1734
RESTAS
Resuelve el crucigrama. Observa el ejemplo.
8
8
4
9
6
8
5
4
713 812 635 – 625 315 781 = 88 496 854
256 632 – 173 981 =
35 261 – 29 747 =
384 362 817 – 343 853 749 =
625 623 649 – 300 629 565 =
1 076 832 – 159 423 =
93 628 – 61 634 =
96 325 – 88 434 =
757 926 943 – 378 855 752 =
81 268 – 61 294 =
Resuelve las restas.
-
725 336.288
611 255.372
-
- 335.66
178.49
382 577.963
171 614.008
4 683.788
2 931.612
935 362.259
625 851.231
- 647.6227
516.8255
-
- 991.377
247.52
555 678.971
313 819.721
-
626 799.183
413 781.527
- 388.73
171.81
-
1 385.453
793.851
MULTIPLICACIONES
Las
partes
de
la
multiplicación son: los
factores, los productos
intermedios y el producto.
7835.72
X 52.01
783572
000000
1567144
3917860
407535.7972
Factores
Resolvemos la multiplicación como lo hacemos
normalmente con números enteros. Después
contamos las cifras que hay después de los puntos de
los dos factores. El resultado debe tener cifras
decimales como los dos factores juntos.
Producto
2 decimales
2 decimales
Productos
intermedios
Colocamos el
punto para que
haya 4
decimales.
Realiza las siguientes multiplicaciones.
640
x325
351
x642
785
x123
315
x222
784
x306
Realiza las siguientes multiplicaciones.
380
x240
642
x963
692
x155
637
x648
107
x231
605
x219
532
x614
881
x347
174
x239
567
x310
238
x675
Realiza las siguientes multiplicaciones.
3 574
X6 843
5 672
X6 212
7 641
X3 621
5 748
X1 432
4 321
X6 887
3 502
X7 613
8 205
X9 311
3 642
X8 840
MULTIPLICACIONES
Resuelve las restas.
128.34
X314.35
174.83
X130.14
651.62
X702.31
381.74
X253.91
174.8
X189.73
836.52
X704.39
364.42
X516.13
719.30
X537.42
MULTIPLICACIONES
Realiza las multiplicaciones.
672 083
X 8.20
502.62017
X .964
.7103259
X 68.3
328.9027
X .45
208 539
X 256
5 681.005
X 7.62
MULTIPLICACIONES
Realiza las multiplicaciones.
64 849
X 325
35 192
X 642
78 815
X 123
78 493
X 306
17 402
X 961
31 571
X 222
DIVISIONES
Las partes de la división
son:
el
divisor,
el
dividendo, el residuo y el
cociente.
0.23
1.9 0.4.38
058
Divisor
01
Cociente
Dividendo
Residuo
Resolvemos
la
división
como
lo
hacemos
normalmente con números enteros. Después
movemos el punto decimal hacia la derecha del
divisor y también movemos el punto decimal del
dividendo la misma cantidad de lugares.
1. Resuelve las siguiente divisiones.
685 38 127
471 64 283
781 38 432
349 78 253
125 49 715
385 82 845
451 72 474
228 35 992
699 48 553
DIVISIONES
2. Resuelve las siguiente divisiones.
60 3 025
74 8 395
85 6 254
35 4 135
43 1 258
38 1 305
78 6 542
13 1 456
93 2 732
DIVISIONES
3. Resuelve las siguiente divisiones.
24 1 782
56 4 873
70 2 552
69 4 215
44 9 729
29 4 362
80 5 624
23 4 640
DIVISIONES
4. Resuelve las siguiente divisiones.
702 53 524
481 72 834
805 22 071
392 97 004
742 83 800
177 31 148
735 39 135
814 54 933
DIVISIONES
5. Resuelve las siguiente divisiones.
7.14 686.3
3.17 711.5
62.5 358.4
83.8 673.6
4.15 373.2
52.2 453.3
17.1 623.1
20.8 838.4
DIVISIONES
6. Resuelve las siguiente divisiones.
52.4 748.3
85.6 976.8
33.4 703.9
35.8 632.5
48.9 248.7
77.4 561.4
91.7 186.4
37.7 797.6
DIVISIONES
7. Resuelve las siguiente divisiones.
43.7 838.3
86.8 251.3
43.5 934.9
54.8 135.4
18.8 179.6
72.3 283.4
8.18 777.7
2.66 487.4
1. El tío Agustín le llevó a su sobrino Arturo una bolsa de
canicas.
lo único que sabe Arturo es que hay 12 canicas de color
amarillo.
Y también sabe lo siguiente:
 La bolsa lleva el doble de canicas azules en relación
con las canicas rojas.
 Las canicas azules son la mitad en relación con la
cantidad de amarillas.
 Hay 2 canicas amarillas más que verdes.
 Las canicas rosas son la mitad en relación con las
verdes.
a) ¿Cuántas canicas hay en total dentro de la bolsa?
_________________________________________________________
b) ¿Cuántas canicas azules hay dentro de la bolsa?
_________________________________________________________
c) ¿Cuántas canicas amarillas hay dentro de la bolsa?
_________________________________________________________
¿Cuántas canicas rosas hay dentro de la bolsa?
_________________________________________________________
d) ¿Cuántas canicas rojas hay dentro de la bolsa?
_________________________________________________________
e) ¿Cuántas canicas verdes hay dentro de la bolsa?
_________________________________________________________
2. Mariela compró 30 paletas, 45 chocolates, y 70
mazapanes. Si planea regalarle a su hermana la mitad de
los mazapanes y 10 paletas; y a su madre le regalará 15
chocolates, ¿Cuántos dulces son para Mariela?
DATOS
OPERACIONES
R:_____________________
3. Doña Rosa es dueña de una dulcería y recibe 91 kg de
dulces a la semana. Si la dulcería de al lado recibe 9
veces lo que recibe doña Rosa, ¿cuántos kilogramos
recibe la dulcería que está al lado de la de doña Rosa?
DATOS
OPERACIONES
R:______________________
4. A María le sobraron 225 chocolates y decidió regalarlos.
Si María repartió entre 15 niños por partes iguales,
¿Cuántos chocolates recibió cada quien?
DATOS
OERACIONES
R:_____________________
5. Claudia se compró un nuevo coche de $250 000. si
Claudia dio un enganche de $50 000 y pagará
mensualidades de $8 000, ¿Cuántos meses deberá pagar
la mensualidad de $8 000 por su coche?
DATOS
OPERACIONES
R:___________________
6. Gabriel ganó $1 000 en una rifa, y le prometió a su novia
que la invitaría al cine para celebrar. Si se gastó $60 por
cada boleto, $40 por las palomitas , $40 por los refrescos y
se gastaron $100 en dulces, ¿Cuánto dinero le queda a
Gabriel? ¿Cuántas veces más podría invitar a su novia en
caso de que siempre se gaste lo mismo?
DATOS
OPERACIONES
R:_______________________
7. Doña Leticia vende paletas heladas a $14 y ha puesto
una promoción que consiste en que si compras 2 paletas,
la segunda tendrá un precio de $7. Si llegaron 5 niños y
cada uno compra 2 paletas, ¿Cuánto dinero gastaran los
5 niños en total? ¿Cuánto dinero ganó Doña Leticia?
¿Cuánto hubiera ganado Doña Leticia si hubiera vendido
todas las paletas a $14?
DATOS
OPERACIONES
R:_____________________
8. Eduardo se compró un reloj de $1500. Si cada semana
recibe $50, ¿Cuántas semanas tuvieron que pasar para
que Eduardo juntara el dinero para comprar el reloj?
DATOS
OPERACIONES
R:_______________________
9. Daniel recorrió en bicicleta 4 kilómetros el miércoles. Si el
lunes recorrió el doble y el martes recorrió solo la mitad,
¿Cuántos kilómetros ha recorrido Daniel en los últimos 3
días?
DATOS
OPERACIONES
R:_______________________
10. José recibe $100 al mes. Ramiro recibe 4 veces más
que José. Alejandro recibe la mitad de lo que recibe
Ramiro.
Luis recibe 3 veces más lo que recibe Alejandro.
Daniel recibe la mitad de lo que recibe José.
a) ¿Quién recibe más dinero?
_________________________________________________________
b) ¿Cuánto dinero recibe Ramiro al mes?
_________________________________________________________
c) ¿Cuánto dinero recibe Alejandro?
_________________________________________________________
¿Cuánto dinero recibe Luis?
_________________________________________________________
d) ¿Cuánto dinero recibe Daniel?
_________________________________________________________
e) ¿Quién recibe menos dinero?
_________________________________________________________
Un número primo se puede dividir exactamente sólo entre
1 y él mismo.
Un número compuesto se puede dividir exactamente
entre otros números, además de 1 y él mismo.
1. Circula con rojo los números primos y con azul los
compuestos.
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
PORCENTAJES
El porcentaje es un número asociado a una razón, que representa
una cantidad dada como una fracción en 100 partes.
1. Obtén el porcentaje de las siguientes cantidades
32% de 1 200 =
40% de 9 685 =
85% de 1 640 =
63% de 16 000 =
75% de 10 500 =
17% de 4 555 =
98% de 7 000 =
23% de 13 225 =
56% de 20 000 =
38% de 8 500 =
65% de 11 000 =
45% de 4 000 =
PORCENTAJES
Determina qué porcentaje representa el segundo valor de la
primera cantidad. Observa el ejemplo.
12 000
7560 x
÷
100
?
a) 12 000
63%
7 560 =___________
b) 5 600
2 800 =___________
c) 2 340
1 070 =___________
d) 17 700
3 540 =___________
e) 25 000
9 000 =___________
f)
4 600 =___________
18 000
g) 940
h) 7 800
i)
600
j)
14 350
235 =___________
2 730 =___________
264 =___________
4 305 =___________
k) 4 600
3 312 =___________
l)
4 950 =___________
9 000
m) 300
n) 21 000
39 =___________
18 900 =___________
Tiendita
“PAOLA”
Calcula el descuento de cada producto y
escribe el precio final de cada uno.
$7 100
15%
Descuento:________ Precio final:________
$5 800
20%
Descuento:________ Precio final:________
$10 500
10%
Descuento:________ Precio final:________
$22 700
40%
Descuento:________ Precio final:________
Obtén los descuentos de los siguientes
artículos y anota cuál es el precio final
-28
OPERACIONES
$3,494
Descuento:___________
Precio final:___________
OPERACIONE S
-70
$60,154
Descuento:___________
Precio final:__________
-26
$4,589
Descuento:__________
Precio final:_________
OPERACIONES
Obtén los descuentos de los siguientes
artículos y anota cuál es el precio final
-52
OPERACIONES
$3,245
Descuento:___________
Precio final:___________
OPERACIONE S
-21
$2,358
Descuento:___________
Precio final:__________
-45
$20,156
Descuento:__________
Precio final:_________
OPERACIONES
Obtén los descuentos de los siguientes
artículos y anota cuál es el precio final
-30
OPERACIONES
$25,999
Descuento:___________
Precio final:___________
OPERACIONE S
-15
$1,570
Descuento:___________
Precio final:__________
-19
$1,001
Descuento:__________
Precio final:_________
OPERACIONES
Potencias
Las potencias son el producto que resulta de multiplicar una misma
cantidad una o varias veces, según el exponente.
Exponente
5² = 25
Base
Potencia
5² = 5 x 5 =25
1. Resuelve las siguientes potencias.
a)
4² = _______
a)
7² = _______
a)
3² = _______
b) 9² = _______
b) 6² = _______
b) 2² = _______
c) 12² =_______
c) 10² =_______
c) 8² =_______
d) 11² =_______
d) 5² =_______
d) 15² =_______
e) 5³ =________
e) 8³ =________
e) 2³ =________
f)
f)
f)
7³ = _______
g) 6³ =________
3³ = _______
g) 10³ =________
4³ = _______
g) 1³ =________
Raíz cuadrada
La raíz cuadrada es lo contrario a elevar un número al cuadrado.
ejemplo:
64 = 8 (8² = 64)
1. Resuelve las siguientes raíces cuadradas.
64 =
25 =
144 =
16 =
36 =
100 =
9 =
4 =
81 =
225 =
49 =
121 =
196 =
400 =
169 =
Raíces cuadradas exactas
4 = 2 porque 2x2 = 4
16 = 4 porque 4x4 = 16
9 = 3 porque 3x3 = 9
25 = 5 porque 5x5 = 25
36 = 6 porque 6x6 = 36
64 = 8 porque 8x8 = 64
49 = 7 porque 7x7 = 49
81 = 9 porque 9x9 = 81
100 = 10 porque 10x10 = 100
121 = 11 porque 11x11 = 121
144 = 12 porque 12x12 = 144
169 = 13 porque 13x13 = 169
196 = 14 porque 14x14 = 196
225 = 15 porque 15x15 = 225
256 = 16 porque 16x16 = 256
Raíz cuadrada
Resuelve las operaciones.
4105
4226
3259
2308
1910
2731
Raíz cuadrada
Resuelve las operaciones.
395196
198714
411993
273103
394276
671978
Medidas de tendencia central
Al describir grupos de diferentes observaciones, con frecuencia es conveniente
resumir la información con un solo número. Es decir, los propósitos de las medidas de
tendencia central son: mostrar en qué lugar se ubica la persona promedio o típica
del grupo, sirve como un método para comparar el puntaje obtenido por una
misma persona en dos ocasiones diferentes y como un método para comparar los
resultados medios obtenidos por dos o más grupos. Las medidas de tendencia
central más comunes son:
•
Moda: es el dato que aparece con mayor frecuencia en una colección de
datos.
•
Media: es el dato que muestra el punto central de una distribución de datos, se
suman los datos y se divide en el número de datos que se tiene.
•
Mediana: es el dato que geométricamente se encuentra a la mitad después de
haber ordenado los datos de menor a mayor.
Encuentra cuál es la moda, la media y la median de las siguientes
situaciones.
1. Se ha realizado una encuesta a 40 personas en la que se les preguntó el
número de personas que conviven en el domicilio habitualmente. Las respuestas
fueron las siguientes.
2. Se realizó una encuesta para saber cuántos televisores tienen en su casa los
alumnos de 6° “B”. Los resultados fueron los siguientes: 2-2-5-3-2-4-4-4-4-5-4}5-3-3-43-4-2-3-3-3-3-2-1-2-3
3. Se realizó un estudio con 100 mujeres mayores de 20 años para saber
el número de hijos que tenían y los resultados fueron los siguientes:
0
13
1
20
2
25
3
20
4
11
5
7
6
4
4. Se realizó una encuesta a 50 hombres para saber cuál es el equipo
más popular de futbol. Los resultados fueron los siguientes:
Barcelona
13
Real Madrid
20
Manchester
United
25
Juventus
20
5. Se realizó u estudio para saber cuántos coches tiene los de 6° “A” y
cuántos coches tiene lo de 6° “B”.
En el salón A los resultados fueron los siguientes: 2-2-1-1-2-1-3-1-3-1-2-0-01-0-1-2-0-2-2-0-3-1-4-2
En el salón B los resultados fueron los siguientes: 3-2-3-2-2-0-1-2-3-4-4-3-32-3-2-1-2-3-2-1-2-1-1-2
6. Se realizó una encuesta para saber cuántas mascotas tienen en su
casa los alumnos de 4° “A”. Los resultados fueron los siguientes: 3-2-2-01-3-3-4-2-0-0-2-1-1-3-1-0-0-2-0-1-0-1-2-0
La probabilidad es un método por el cual se obtiene la frecuencia de
un acontecimiento determinado mediante la realización de un
experimentos aleatorios, de los que se conocen los resultados posibles.
1. Casandra va a lanzar un dado y quiere saber qué probabilidad hay
de que pase lo siguiente:
a) Que caiga 5 = ____________________________
b) Que caiga par = __________________________
c) Que no caiga par =_______________________
d) Que caiga un número mayor a 3 = ________
e) Mayor a 6 =_______________________________
f)
Menor o igual a 4 = _______________________
g) Mayor a 1 =_______________________________
h) Menor o igual a 6 =________________________
Convierte las fracciones adquiridas a
decimales para comprobar tu resultado.
2. Carlos acaba de regalarle a su sobrino Hernán un a bolsa de
canicas, en la cual se encuentran 4 canicas azules, 5 canicas verdes, 8
canicas rojas y 6 canicas amarillas, 1 canica blanca y 1 canica rosa.
¿Cuál es la probabilidad de que Hernán saque una canica…
a) Azul?______________________________________
b) Blanca?___________________________________
c) Que no sea rosa?__________________________
d) Que no sea amarilla?______________________
e) Que no sea ni amarilla ni azul?______________
f)
Roja?______________________________________
g) Verde o rosa? _____________________________
h) Roja o azul? _______________________________
La estadística es una herramienta que estudia usos y análisis
provenientes de una muestra representativa de datos.
1. Juan y Pedro decidieron realizar un estudio en su empresa acerca de
cuántos baños tiene en casa cada empleado del departamento de
finanzas y obtuvieron lo siguiente:
a) Empresa de Pedro
Completa la tabla. Observa la tabla.
1
2
2
3
2½
1
3
10
3½
1
4
3
4½
1
5
3
6
1
2/25 = 0.08
3/25 = 0.12
a) Empresa de Juan Pablo. Completa la tabla.
2
1
3
3
4
17
5
4
6
1
2. José Antonio ha registrado las temperaturas de todo el mes de
marzo. Los resultados fueron los siguientes:
20°
5
23°
6
25°
9
26°
3
27°
2
29°
6
3. La maestra Mariana quiere calificar al grupo 2° “C” con estos
criterios: bueno (9-10); regular (8-7); y malo (5-6). Las calificaciones son
las siguientes:
10
6
9
8
8
11
7
6
6
7
5
2
Una tabla de variación proporcional se emplea para ver la relación entre dos
cantidades que aumentan o disminuyen proporcionalmente. Es decir, es una
variación funcional especial que puede ser directa o inversa.
Ejemplo: Mariana recorre 56 km en 2 días.
¿Cuánto recorrerá en 8 días?
56 km
2 días = x km
8 días
(58 x 8) /2 = x = 224 km
1. Resuelve los siguientes ejercicios. Guíate del ejemplo anterior.
a) Un deposito de agua se llena en 2.25 horas empleando 5 llaves de agua,
mientras que empleando 3 llaves, el deposito de agua se llena en 3.75. ¿Cuánto
tiempo tardará en llenarse el deposito de agua empleando únicamente una sola
llave?
Llaves de agua
5
3
Tiempo
2.25
3.75
1
b) El encargado de compras de una empresa adquirió los empaques de los
productos que se fabrican, desafortunadamente tuvo un problema con su
computadora y no se guardaron los últimos cambios, ayúdale a calcular los datos
faltantes.
Semana 1
Empaques
700
Total a pagar
$300
Semana 2
Semana 3
Semana 4
500
125
$550
c) Una persona lleva el registro de cuántos litros de gasolina gasta cada semana. Si
se le pidieron algunos datos, ¿Cómo completarías la tabla sabiendo que el gasto es
proporcional?
Semana 1
Litros de gasolina
50
Total a pagar
$510
Semana 2
Semana 3
Semana 4
42
$410
$320
d) Un automóvil consume 9 litros de gasolina cada 120 kilómetros. Calcula y
completa la tabla.
Litros de gasolina
9
45
Distancia
120
600
50
65
550
1.
Resuelve y haz un dibujo de los siguientes problemas.
1. Un edificio de 15.4 metros de altura da una sombra de 4.68 metros. La casa de al
lado produce una sombra de 1.76 metros. ¿Cuál es la altura de la casa?
R:_______________________
2. Una persona mide 1.72 metros de altura y produce una sombra de 72
centimetros; al lado suyo, hay un poste de luz que produce una sombra de 2.42
metros. ¿Cuál es la altura del poste de luz?
R:________________________
3. Unos niños decidieron ir a comprar y armaron su tienda de campaña justo al lado
de un árbol que tiene una altura de 1.78 metros y hace una sombra de 5.2 metros.
Si la tienda de campaña produce una sombra de 2.1 metros. ¿Cuál será la altura
de la tienda de campaña?
R:________________________
4. Carlos y Tomás miden y pesan proporcionalmente. Carlos tiene una altura de 1.85
metros y Tomás mide una altura de 1.76 metros. Si Tomás quiere averiguar cuál es su
peso y sabe que Carlos pesa 75 kilogramos, ¿Cuánto pesa Tomás?
R:_______________________
Las fracciones y los decimales son simplemente dos formas diferentes de expresar el
mismo valor, pero ¿Cómo convertimos una fracción a decimal? Muy sencillo,
solamente tenemos que dividir el numerador entre el denominador.
1.
Convierte de fracciones a decimal. Fíjate en el ejemplo.
2
3
3
4
4
6
2
7
9
10
0.66
2
5
5
8
1
4
4
5
7
80
para convertir de decimal a fracción, simplemente tomamos la parte decimal y la
colocamos como el numerador de la fracción y para nuestro denominador
utilizamos 10, 100, 1 000, …. De acuerdo con la cantidad de dígitos que tenga
nuestro decimal , es decir, si tiene 1 digito usamos 10, dos dígitos 100, así
sucesivamente. Por tanto, la cantidad de ceros en el denominador depende de la
cantidad de dígitos en el decimal.
2. Convierte de decimal a fracción y reduce a su máxima expresión.
0.3
3
10
0.125
0.45
0.75
0.60
0.5
0.843
0.42
0.483
0.493
las fracciones equivalentes tienen el mismo valor, aunque sean diferentes.
2
Ejemplo: 1 = 4 debido a que su valor decimal es el mismo: 1 = 0.5, mientras
2
2
2 = 0.5 también.
1.
de fracciones a decimal. Fíjate en el ejemplo.
QueConvierte
4
1.
Relaciona las columnas.
10
15
18
54
2
8
6
4
9
27
20
30
10
12
5
1
12
8
5
6
8
10
18
21
12
20
60
180
6
7
4
5
20
4
8
32
30
90
3
5
2. Encierra en un círculo la fracción equivalente.
3
5
12
15
15
25
7
10
6
12
1
2
5
8
13
16
9
10
16
18
4
5
18
20
12
16
8
15
2
6
3
4
1
4
25
100
18
40
45
100
4
6
6
4
20
30
17
10
1
3
3
9
15
60
17
51
1. Coloca el signo <, > o =, según corresponda y transforma a
decimal las dos fracciones para comprobar. Guíate del
ejemplo.
1
2
__________
3
2
=
0.5 < 1.5
3
6
__________
4
8
=
________
2
4
2
3
3
2
4
7
=
________
=
________
=
________
=
________
4
5
1
4
6
4
5
8
__________
__________
__________
__________
4
11
__________
3
4
=
________
6
8
__________
7
5
=
________
Comparación de fracciones
1. Escribe los signos <,> o = según corresponda.
1
2
7
16
3
5
6
10
2
3
4
5
2
8
1
4
4
5
1
2
5
8
3
6
3
15
1
5
1
4
1
3
14
16
6
8
7
10
6
7
4
9
3
4
15
22
7
11
6
12
8
9
4
8
6
9
6
7
5
8
4
7
6
3
8
15
2
4
3
16
2
8
5
8
2
3
5
8
2
3
8
20
4
10
Ordenar fracciones
1. Ordena en los recuadros las siguientes fracciones y enteros de
menor a mayor.
a)
6 , 2 , 7 ,
10 5 4
b)
c)
<
1 , 3 , 1 , 7 ,
3 12 2 6
2
8 , 6 , 10 ,
2 3 6
d)
e)
3
2
1,
1,
7
5
3 , 5 , 7 ,
4 8 2
4 , 8 , 4 , 15 , 2
9 15 5 45 3
<
1
<
, 5
6
<
<
<
<
<
<
<
<
<
<
<
<
<
<
<
<
<
El mínimo común múltiplo (m.c.m) de dos o más números es el menor de sus
múltiplos comunes que no sea cero. Para obtenerlo se necesita:
a) Se descomponen esos números en sus factores primos.
b) Se multiplican todos los factores comunes y no comunes con sus mayores
exponentes.
1. Saca el mínimo común múltiplo de las siguientes
cantidades. Recuerda que debes poner divisores para que
todos los números de la izquierda lleguen a uno.
8, 12, 18
4 6 9
2 3 9
1 3 9
1 3
1
2
2
2
3
3
(En este caso todos se dividen
entre 2)
(como 9 no tiene mitad, pasa
igual)
(en este caso se llega a 1 en
un número)
(en ente caso se divide entre
3)
(en este caso se llega a 1)
(por último se multiplican los
factores 2 x 2 x 2 x3 x 3
24, 36, 45
m.c.m = _____
m.c.m = 72
20, 30, 40
6, 8, 15
m.c.m = _____
m.c.m = _____
120, 90, 60
12, 16, 18
m.c.m = _____
m.c.m = _____
5, 8, 10
4, 6, 8
m.c.m = _____
m.c.m =
4, 6, 9
10, 12, 18
m.c.m = _____
m.c.m = _____
5, 10, 12
3, 7, 9
m.c.m = _____
m.c.m = _____
9, 12, 18
12, 15,30
m.c.m = _____
m.c.m = _____
El máximo común divisor (m.c.d) de dos o más números naturales o enteros (no
números con decimales es el número más grande que los divide sin dejar resto.
1.
Obtén el máximo común divisor de las siguientes cantidades.
Observa el ejemploRecuerda que a diferencia del m.c.m, aquí debes dividir todas las
cantidades con un mismo número, cuando esto ya no se te sea
posible, significa que has acabado el ejercicio.
60, 80, 40 2
20 40 20 2
21 15 10 5
3 4 2
140, 180, 50
1.
2.
3.
4.
Todos se pueden dividir en 2
Todos se pueden dividir en 2
Todos se pueden dividir en 5
Se multiplican todos los
factores: 2 x 2 x 5 = 20
m.c.d = _____
m.c.d = 20
10, 15, 20
100, 20, 80
m.c.d = _____
m.c.d = _____
13, 26, 39
30, 90, 60
m.c.d = _____
m.c.d = _____
380, 420
225, 300
m.c.d = _____
m.c.d = ______
35, 85, 25
18, 24, 36
m.c.d = _____
m.c.d = _____
80, 120, 200
48, 12
m.c.d = _____
m.c.d = _____
14, 36, 60
15, 28, 40
m.c.d = _____
m.c.d = _____
1.
Realiza las siguientes sumas de fracciones y reduce a su mínima
expresión. Guíate en el ejemplo.
a) Obtén el mínimo común múltiplo de los denominadores para tener
denominador en el resultado.
5, 8
5 4
5 2
5 1
1
2
2
2
5
m.c.m =2 x 2 x 2 x 5 = 40
b) Divide el denominador del resultado entre el primer denominador y
múltiplo por el numerador. Después haz lo mismo con el segundo
denominador y numerador.
c) Finalmente, se suman las fracciones y si el resultado es una fracción
impropia se convierte a mixta.
11
2
7
16 + 35 51
=
=1
+
=
40
40
5
8
40
7
5
=
+
10
16
2
7
=
+
5
8
2
3
=
+
5
10
1
6
=
+
2
7
2. Resuelve las siguientes sumas de fracciones y reduce a su mínima
expresión.
1
14
=
+
2
4
5
1
=
+
2
6
5
3
=
+
3
5
10
1
=
+
8
4
16
11
=
+
3
4
6
21
=
+
9
3
4
8
+
3
8
4
7
=
+
3
6
2
9
+
4
2
=
=
3
9
=
+
6
8
3. Une las sumas de fracciones con su resultado.
8
3
+
3
8
=
25
28
1
14
+
3
16
=
11
8
1
+
7
8
=
2
1
6
+
7
8
=
2
2 21
2
3
6
1 =
+
3
10
1
2 10
6
15
=
+
4
3
2
3
4
21
32
=
+
3
8
1 39
40
3
10
=
+
4
5
6
8
10
=
+
12
7
1 15
56
12
20
=
+
3
3
8
1
2
4. Realiza las siguientes sumas de fracciones y reduce a su mínima
expresión.
2
4
2
+
+
=
5
6
10
7
21 17
+
+
=
3
5
3
2
7
2
+
+
4
5
6
=
3
1
9
+
+
4
3
4
=
4
3
11
+
+
=
6
6
6
1
2
3
+
+
4
5
6
=
6
2
7
+
+
1
4
5
3
2
11
+
+
=
6
9
5
=
9
10 11
+
+
=
5
6
4
14
13
4
+
+
3
6
1
=
1
2
4
+
+
3
5
6
5
7
2
+
+
3
5
3
=
=
6
8
12
+
+
=
4
5
6
3
13
3
+
+
=
4
6
12
11
11
5
+
+
3
6
6
=
2
7
9
+
+
4
5
4
2
3
1
+
+
3
5
9
=
5
13 16
+
+
=
4
6
5
=
1.
Sacar el m.c.m de los denominadores para tener denominador de
resultado.
5, 7 5
1 7 7
1
m.c.m =5 x 7= 35
Divide el denominador del resultado entre el primer denominador y
múltiplo por el numerador. Después haz lo mismo con el segundo
denominador y numerador.
Finalmente, se suman las fracciones y si el resultado es una fracción
impropia se convierte a mixta. ¡Recuerda simplificar las fracciones!
4
1
=
5
7
23
28 - 5
=
35
35
1. Resuelve las siguientes restas de fracciones. Recuerda reducir a su mínima expresión.
2
3
4
=
7
3
1
=
10
12
9
3
15
8
=
4
2
3
5
=
9
2
4
6
=
2
2
3
5
=
11
11
=
6
3
13
5
6
4
=
2. Resuelve las siguientes restas de fracciones. Recuerda reducir a su
mínima expresión.
11
7
5
4
=
11
4
4
3
=
6
3
4
2
=
1
2
2
5
=
18
4
5
3
=
10
10
=
2
5
7
11
6
5
=
8
17
=
5
13
4
=
7
3
1
=
10
12
2
3
9
3
=
20
18
4
2
9
7
=
2
1
3
2
=
7
3
8
4
=
1
1
8
6
=
6
3
5
2
=
3. Realiza las siguientes sumas de fracciones y reduce a su mínima
expresión.
17
- 3 - 1
4
5
4
=
15
- 3 - 2
3
4
8
=
12 - 1
- 1
3
5
3
=
13 - 5
- 1
2
6
7
=
5
1
1
2
=
4
3
- 1 =
1
7
10
16
3
- 2
2
2
5
=
- 8
9
20
4
- 1 =
3
5
10
10
5
13
=
1
7
8
8
8
9
1
3
5
3
5
=
7
7
2
8
- 1
6
=
18
5
3
+
+
3
7
3
=
4
2
6
1
3
4
=
12
3
4
16
8
3
=
4
3
2
2
5
9
=
2
1
6
1
5
7
=
- 1 - 2
4
8
20
3
5
5
-
2
1
=
=
Recuerda que las multiplicaciones de fracciones se realizan
multiplicando numerador por numerador, y denominador por
denominador. Si el resultado es una fracción impropia se convierte a
fracción mixta. ¡Acuérdate de simplificar tus resultados!
40
20
5
8
10
5
2
=
=
=
x
=
=1
24
12
6
4
6
3
3
1. Resuelve las siguientes multiplicaciones de fracciones. Recuerda reducir a su
mínima expresión.
1 x 4
=
3
8
2 x 5
=
6
3
3 x 1
5
4
=
7 x 3
4
4
3 x 2
3
5
=
13
5
=
5
3
8 x 9
2
5
=
11 x 3
=
2
4
=
2. Resuelve las siguientes multiplicaciones
reducir a su mínima expresión.
de fracciones. Recuerda
7 x 7
=
4
2
6 x 8
2
2
5 x 8
4
2
3 x 2
=
2
10
=
=
4 x 3
=
3
2
10 x 7
2
6
=
8 x 2
2
4
=
4 x 8
5
1
=
2 x 9
6
9
=
3
13
6
3
=
1 x 12
=
5
8
3 x 6
=
4
14
3. Realiza las siguientes multiplicaciones de fracciones y reduce a su
mínima expresión. Luego, encuentra los productos en la sopa de
fracciones.
1 x 2
=
5
2
2 x 1
7
3
=
2 x 2
5
3
=
3 x 3
7
2
=
1 x 9
=
16
3
4 x 2
7
5
=
3 x 7
4
2
=
3 x 7
=
8
10
3 x 5
6
10
=
3
8
x
7
5
=
5
16
3
15
8
4
1
4
21
10
4
1
2
11
4
15
8
21
10
14
8
5
1
6
21
8
16
18
24
38
32
5
39
30
2
15
9
36
21
80
9
16
2
9
8
35
4
5
4
5
12
8
1
7
3
16
24
35
5
16
2
3
4
6
1
19
3
8
3
7
9
14
2
9
8
23
3
7
80
21
Recuerda que las divisiones de fracciones consisten en multiplicar
cruzado; es decir, el primer numerador por el segundo denominador y
el producto se coloca en el numerador del resultado. Y el segundo
numerador por el primer denominador y el producto se coloca en el
denominador del resultado. Si el resultado es una fracción impropia se
convierte a fracción mixta. ¡No olvides simplificar tus resultados!
36
9
3
=
=
÷
3 12
1
4
1. Resuelve las siguientes divisiones de fracciones. Recuerda reducir a su mínima
expresión.
1
8
=
÷
8
3
1
10
÷ 5
9
=
2
7
÷
7
5
=
3
6
÷
5
7
=
5
8
÷
7
13
=
9
15
=
÷
11
12
20
5
=
÷
30
4
14
7
÷ 2 =
3
2. Resuelve las siguientes divisiones de fracciones. Recuerda reducir a su mínima
expresión.
7
9
=
÷
16
3
2
7
÷ 2
8
=
5
8
=
÷
12
9
2
3
÷
9
7
=
=
5
4
÷
4
3
=
2
24
÷
4
30
1
3
÷
4
9
=
7
15
÷ 8 =
18
9
8
÷
3
15
=
9
12
=
÷
13
7
6
17
÷
8
4
=
2
17
÷ 5 =
13
3. Resuelve las siguientes divisiones de fracciones. Recuerda reducir a su mínima
expresión.
3
16
=
÷
9
2
5
9
÷ 7
12
=
25
7
=
÷
18
2
9
8
÷
6
8
=
14
5
=
÷
17
6
8
9
÷
2
3
=
20
18
=
÷
5
4
12
14
÷ 6 =
8
4
7
÷
9
18
=
21
36
=
÷
7
18
8
12
÷
3
5
=
4
3
÷ 9 =
13
1.
Una persona cuyo peso era de 70 kg se sometió a una dieta,
durante 3 semanas bajó las siguientes cantidades.
Semana 1: 2 ½ kg
Semana 2: 1 1/6 kg
Semana 3: 3 1/5 kg
¿Cuál es el peso actual de la persona después de estas 3 semanas?
DATOS
OPERACIONES
R:_________________________
2. A Roberto le pagan $120 por cada hora que trabaja. Si en un día
trabajó 3 2/3 horas, ¿Cuánto le pagaron ese día a Roberto?
DATOS
OPERACIONES
R:___________________________
3. Julián corrió ¼ de milla el primer día de entrenamiento. El segundo
día corrió otro ¼ de milla. El tercer día corrió 2/3 de milla. ¿Cuánto
corrió Julián en esos tres días?
DATOS
OPERACIONES
R:_________________________
4. En una escuela hay 120 alumnos en 4° de primaria, 90 alumnos en 5°
y 60 alumnos en 6°. Si se quieren hacer equipos mezclando alumnos
de los 3 grados, ¿Cuál es el máximo de equipos que se pueden
formar? y ¿Cuántos alumnos de cada grado habría en cada equipo?
DATOS
OPERACIONES
R:___________________________
5. En una fundación se donaron 200 bolsas de arroz, 180 bolsas de frijol
y 120 bolsas de aceite. La fundación quiere hacer paquetes para
donar a familias de escasos recursos. ¿Cuántos paquetes se pueden
llevar dividiendo los productos y que no sobre ninguno? Y ¿Cuántos
productos de cada uno llevaría cada paquete?
DATOS
OPERACIONES
R:_________________________
6. Para el altar del día de Muertos del colegio se compraron 180 flores
amarillas, 120 flores moradas y 90 flores blancas. Si se quieren hacer
varios ramos, ¿Cuál es el máximo de ramos que se pueden realizar
incluyendo todos los tipos de flores? Y ¿Cuántas flores de cada color
llevaría cada ramo?
DATOS
OPERACIONES
R:___________________________
7. El viernes se reunieron 17 empresarios para negociar acerca de unos
hoteles. En la reunión hubo ponche. Si cada hombre consumió 2 ½
litros, ¿Cuántos litros de ponche se consumieron en la reunión?
DATOS
OPERACIONES
R:__________________________
La jerarquización de operaciones determina el orden de tu
procedimiento al hacer tus operaciones.
1. Paréntesis
2. Números elevados y raíces
3. Multiplicación y división
4. Sumas y restas
1. Resuelve las siguientes operaciones.
a) 2² + 3 x 5 + 3 =____________
b) 9 x 9 + 8 x 4² =____________
c) 35 – 24 ÷ 12 =_____________
d) 7² + 8 x 2 =_______________
e) 51 ÷ 3 + 17 – 4 =__________
f) 4 + (2 + 2) x 7 – 20 =_______
g) 64 ÷ 4 + 15 ÷ 3 =__________
h) 3³ ÷ 9 + 70 =______________
i) 8 + 5 x 13 – 16 =__________
j) 90 ÷ 15 + 40 - 5² = ________
Conversión de unidades: la conversión de unidades es la
transformación del valor numérico de una magnitud física, expresado
en una cierta unidad de medida, en otro valor numérico equivalente
y expresado en otra unidad de medida de la misma naturaleza.
Las medidas de capacidad sirven para medir los líquidos. La unidad
principal para medir la capacidad en el litro ( ).
Múltiplos
Unidad
Kilolitro
Hectolitro
Decalitro
1000 litros
100 litros
10 litros
Submúltiplos
Litro
Decilitro
Centilitro
Mililitro
0.1 litros
0.01 litros
0.001 litros
Para convertir de una unidad mayor a una menor se multiplica y para
convertir de una menor a una mayor se divide.
1. Escribe con número las siguientes cantidades. Observa el ejemplo.
a) Ciento cincuenta litros
150 l
_____________
b) Ochocientos treinta y cinco mililitros
_____________
c) Siete decilitros
_____________
d) Cuarenta y nueve kilolitros
_____________
e) Trescientos sesenta y tres decalitros
______________
f)
______________
Dieciséis hectolitros
g) Setecientos veinticinco centilitros
______________
h) Quinientos setenta y cuatro decalitros
_____________
i)
Mil cien litros
______________
j)
Doscientos cincuenta y cinco mililitros
______________
2. Realiza las siguientes conversiones. Observa el ejemplo.
40 l = 40 000 ml
a) 400 litros ------------ mililitros = __________________________
b) 60 000 centilitros-------------- decalitros =_______________
c) 8 kilolitros ---------- decilitros = _________________________
d) 90 decalitros ------ centilitros =________________________
e) 7 500 000 mililitros--- hectolitros =_____________________
f)
9 hectolitros -------- mililitros =__________________________
g) 645 decalitros ------- kilolitros =________________________
h) 600 decalitros -------- decilitros =______________________
i)
90 centilitros ---------- mililitros =________________________
j)
368 hectolitros ------ decalitros =______________________
Ubica el punto decimal, eso te ayudará a
convertir la medida de unidad de una forma
más rápida.
3. Relaciona las columnas.
1.
4 500.0
a) 65 litros a decalitros
2.
1 000 000
b) 100 000 mililitros a litros
3.
100
c) 40 kilolitros a decilitros
4.
6.5
d) 1 150 centilitros a decalitros
5.
50 000
e) 500 hectolitros a litros
6.
400 000
f)
7.
30.00
g) 25 decilitros a centilitros
8.
1.150
h) 3 000 litros a hectolitros
9.
250
i)
1 kilolitro a mililitro
10. 88.50
j)
45 000 centilitros a decilitros
8 850 decalitros a kilolitros
La unidad principal para medir el peso es el gramo (g).
Múltiplos
Kilogramo
kg
1000
gramos
Hectogramo
hg
100 gamos
Unidad
Decagramo
Dg
10 gramos
Gramo
g
Submúltiplos
Decigramo
dg
0.1 gramos
Centigramo
cg
0.01 gramos
Miligramo
mg
0.001
gramos
Para hacer conversiones, igual que en todas las medidas del Sistema
Métrico Decimal, se multiplica de mayor a menor y se divide de menor
a mayor.
La unidad más usada de las medidas de peso es el kilogramo.
1. Escribe con número las siguientes cantidades. Observa el ejemplo.
a) Ochocientos cuarenta gramos
840 g
_____________
b) Mil cien centigramos
_____________
c) Setenta y nueve kilogramos
_____________
d) Doscientos veinticinco decagramos
_____________
e) Quinientos quince hectogramos
______________
f)
______________
Trescientos treinta miligramos
g) Novecientos diecisiete decigramos
______________
h) Cuatrocientos ochenta y cinco decagramos
______________
i)
Seiscientos kilogramos
______________
j)
Tres mil quinientos miligramos
______________
2. Realiza las siguientes conversiones. Observa el ejemplo.
3.00 hg
a) 300 gramos ------------ hectogramos = ______________________
b) 10 000 centigramos -------------- gramos =___________________
c) 750 decigramos ---------- centigramos = ____________________
d) 400 hectogramos ------ kilogramos =________________________
e) 250 gramos--- decagramos =_____________________________
f)
5 000 decigramos -------- gramos =________________________
g) 3 450 decagramos ------- hectogramos =__________________
h) 90 kilogramos -------- miligramos =_________________________
i)
6 200 centigramos ---------- decigramos =__________________
j)
800 000 miligramos ------ decagramos =____________________
3. Relaciona las columnas.
a) 600 decagramos a kilogramos
b) 18 hectogramos a miligramos
c) 20 000 centigramos a gramos
d) 400 decigramos a miligramos
e) 50 hectogramos a decigramos
f)
370 decagramos a centigramos
g) 45 000 gramos a kilogramos
h) 1 200 decigramos a hectogramos
i)
9 kilogramos a centigramos
j)
650 decagramos a centigramos
1.
200.00
2.
45.000
3.
370 000
4.
40 000
5.
1.200
6.
650 000
7.
1 800 000
8.
6.00
9.
50 000
10. 900 000
La unidad principal para medir la longitud es el metro (m).
Múltiplos
Kilómetro
km
1000
metros
Hectómetro
hm
100 metros
Unidad
Decámetro
Dam
10 metros
Metro
m
Submúltiplos
Decímetro
dm
0.1 metros
Centímetro
cm
0.01 metros
Milímetro
mm
0.001
metros
Para convertir de una unidad mayor a una unidad menor se multiplica
y para convertir de una unidad menor a una mayor se divide.
1. Escribe con número las siguientes cantidades. Observa el ejemplo.
a) Setecientos sesenta y dos metros
762 m
_____________
b) Treinta y cinco kilómetros
_____________
c) Seiscientos cincuenta decímetros
_____________
d) Trescientos noventa y cuatro decámetros
_____________
e) Quinientos treinta y tres hectómetros
______________
f)
______________
Doscientos veinticinco centímetros
g) Mil milímetros
______________
h) Novecientos noventa decímetros
______________
i)
Ciento quince metros
______________
j)
Cuatrocientos ochenta y tres metros
______________
2. Realiza las siguientes conversiones. Observa el ejemplo.
15 000 m
a) 150 hectómetros -------------------- metros = ______________________
b) 300 000 milímetros -------------- decámetros =___________________
c) 10 kilómetros -------------------- centímetros = ____________________
d) 500 000 milímetros ------ decámetros =________________________
e) 800 centímetros--- decímetros =_____________________________
f)
736 metros ------------------- milímetros =________________________
g) 12 000 decímetros ----------------- kilómetros =__________________
h) 170 metros --------------- decámetros =_________________________
i)
10 kilómetros ----------------------- decímetros =__________________
j)
40 decámetros -------------- hectómetros =____________________
3. Relaciona las columnas.
a) 4 kilómetros a decámetros
b) 17 000 milímetros a metros
c) 80 hectómetros a centímetros
d) 5 500 decímetros a decámetros
e) 600 metros a hectómetros
f)
8 250 milímetros a decímetros
g) 400 decámetros a centímetros
h) 9 750 hectómetros a kilómetros
i)
65 metros a milímetros
j)
333 decímetros a decámetros
1.
975.0
2.
400 000
3.
55.00
4.
17.000
5.
65 000
6.
6.00
7.
82.50
8.
3.33
9.
40 000
10. 800 000
Las unidades de tiempo sirven para medir años, meses, semanas, días,
etc. Las más comunes son:
 Un milenio = 1 000 años
un mes = 4 semanas = 30 o 31 días
 Un siglo = 100 años
una semana = 7 días
 Una década = 10 años
un día = 24 horas
 Un lustro = 5 años
una hora = 60 minutos
 Un año = 12 meses
un minuto = 60 segundos
Para convertir de una unidad mayor a una mayor se divide con base
a su equivalencia y para convertir de una unidad mayor a una menor
se multiplica.
1. Realiza las siguientes conversiones.
7 siglos = ____________ años
12 minutos = ________ segundos
9 meses =____________ días
20 horas =____________ minutos
4 décadas =_________ años
3 siglos =______________ lustro
8 días =______________ horas
2 años =______________ meses
5 lustros =____________ años
38 semanas =_________ días
2. Relaciona las columnas.
a)
2 milenios + 3 siglos + 5 décadas + 7 lustros
b)
1 milenio + 4 siglos + 3 lustros + 9 años
c)
8 milenios + 10 siglos + 1 década + 4 años
d)
13 milenios + 9 décadas + 5 lustros + 8 años
e)
1 milenio + 2 lustros + 17 años
f)
5 milenios + 8 siglos + 11 décadas + 6 lustros
g)
31 siglos + 14 décadas + 20 lustros + 13 años
h)
4 milenios + 40 siglos + 18 décadas + 1 lustro
i)
9 milenios + 80 décadas + 12 lustros + 27 años
j)
87 décadas + 35 lustros + 94 años
 9 014 años
 3 253 años
 1 027 años
 1 424 años
 1 139 años
 2 385 años
 13 123 años
 9 887 años
 8 185 años
 5 940 años
Un pie equivale a 30.48 cm que es igual a 0.3048 m.
Para convertir del Sistema Métrico Decimal (S.M.D) al Sistema Inglés de
Medidas (S.I.M) se divide. Y para convertir del S.I.M al S.M.D se
multiplica.
1. Realiza las siguientes conversiones.
a) 60 pies----------------metros ________________
b) 200 metros----------pies ___________________
c) 250 pies--------------metros ________________
d) 88 metros------------pies ___________________
e) 100 pies--------------metros ________________
f)
103 metros----------pies ___________________
g) 243 pies--------------metros ________________
h) 90 metros------------pies ___________________
i)
14 000 pies----------metros ________________
j)
160 metros----------pies ___________________
Una libra equivale a 0.4535 kg
1. Realiza las siguientes conversiones.
a) 60 libras------------------------kilogramos ________________
b) 46 kilogramos-------------------libras ___________________
c) 76 libras-----------------------kilogramos ________________
d) 100 kilogramos-----------------libras ___________________
e) 83 libras-----------------------kilogramos ________________
f)
37 kilogramos-------------------libras ___________________
g) 450 libras----------------------kilogramos ________________
h) 25 kilogramos------------------libras ___________________
i)
91 libras-----------------------kilogramos ________________
j)
55 kilogramos------------------libras ___________________
1. Armando es dueño de 615 vacas y aporta 45% de su producción a
Leches La Vaquita y el otro 55% a Gold Milk. Si una vasa produce 37
litros de leche al día, ¿Cuántos litros producirán todas sus vacas en
una semana? Y ¿Cuántos litros le aporta a Leches La Vaquita en una
semana? Y ¿Cuántos litros le aporta a Gold Milk en una semana?
DATOS
OPERACIONES
R:_________________________
2. Mariana tiene un peso de 75 kilogramos y su nutrióloga le ha
otorgado una nueva dieta y ella misma se ha creado una rutina de
ejercicios, si Mariana quema 700 gramos al día, ¿Cuánto pesará en 30
días? Y ¿Qué porcentaje de su peso habrá eliminado?
DATOS
OPERACIONES
R:___________________________
3. Si al dueño de una tienda al día le llegan 2 bolsas de frijol de 4 kg
c/u; 5 bolsas de arroz de 1 kg c/u; 3 botellas de 1 litro de aceite c/u; y
6 botellas de leche de 1 litro c/u. y él vende cada kilogramos a $15 y
cada litro a $12.
¿Cuántos kilogramos le llegan al día en total?
¿Cuántos litros le llegan al día en total?
¿Cuánto dinero gana al día considerando que vende todo?
DATOS
OPERACIONES
R:_________________________
4. Sebastián quiere escalar una montaña de 3.5 kilómetros de altura. Si
Sebastián avanza 72 centimetros por cada paso que da, ¿Cuántos
pasos tendrá que dar Sebastián para llegar a la cima de la montaña?
DATOS
OPERACIONES
R:___________________________
5. Carlos pesa 174 libras y mide 6 pies; mientras que tomas pesa 81
kilogramos y mide 1.77 metros. ¿Quién pesa más y cuanto es la
diferencia de peso entre los dos? Y ¿Quién es más alto y cuánto es la
diferencia de altura ente los dos?
DATOS
OPERACIONES
R:__________________________
Un ángulo es la parte del plano comprendida entre dos semirrectas que tienen el
mismo punto de origen o vértice. Los ángulos se miden con el transportador, el
cual está dividido en grados (°). Por su abertura, un ángulo puede ser:
 Ángulo recto: cuyos lados son perpendiculares entre sí, mide 90°
 Ángulo agudo: en el que tiene menor abertura que un ángulo recto, es decir,
mide menos de 90°
 Ángulo obtuso: es el que tiene mayor abertura que el ángulo recto, es decir,
mide más de 90°
 Ángulo llano: es aquel que mide 180°
 Ángulo completo: es aquel que mide 360°
1. Escribe el nombre del ángulo, según las medidas que se indican.
a) 90° ___________________
a) 45° ___________________
b) 65° ___________________
b) 120° __________________
c) 112° __________________
c) 174° __________________
d) 25° ___________________
d) 10° ___________________
e) 63° ___________________
e) 39° ___________________
f)
f)
99° ___________________
94° ___________________
g) 180° __________________
g) 100° __________________
h) 150° __________________
h) 89° ___________________
i)
80° ___________________
i)
163° __________________
j)
135° __________________
j)
180° __________________
2. Con ayuda de tu transportador traza los siguientes ángulos.
Traza un ángulo de 25°
Traza un ángulo de 95°
Traza un ángulo de 50°
Traza un ángulo de 100°
Traza un ángulo de 60°
Traza un ángulo de 130°
Traza un ángulo de 10°
Traza un ángulo de 115°
Traza un ángulo de 64°
Traza un ángulo de 160°
Traza un ángulo de 45°
Traza un ángulo de 145°
Un prisma es determinado por dos polígonos paralelos y congruentes que se
denominan bases y por tantos paralelogramos como los lados que tengan las
bases, denominadas caras.
Una pirámide es un poliedro limitado por una base, que es un polígono (la cara
inferior) y por varias caras laterales, que son triángulos con vértices coincidentes
en un punto denominado cúspide. Por ejemplo: un cilindro es un prisma y un cono
una pirámide.
1. Identifica los siguientes cuerpos geométricos y escribe el nombre
que reciben cada uno.
Área de la base
15.5 cm
A=b x h
2
A= 9 x 9
2
A= 81 /2 = 40.5 cm²
Volumen
V= ab x h
V= 40.5 cm² x 15.5 cm²
V= 627.75 cm³
9 cm
9 cm
1. Obtén el volumen de los siguientes prismas.
Área de la base
Volumen
42 cm
V= ab x h
22 cm
Área de la base
Volumen
50 cm
V= ab x h
12 cm
24 cm
Obtén el volumen de los siguientes prismas.
Área de la base
Volumen
30 cm
V= ab x h
7.5 cm
14 cm
Área de la base
Volumen
45 cm
V= ab x h
12 cm
24 cm
Área de la base
Volumen
19.5 cm
V= ab x h
10 cm
13 cm
Área de la base
A=b x h
2
A= 7 x 5
2
A= 35 /2 = 17.5 cm²
5 cm
7 cm
Volumen
V= ab x h
3
V= 17.5 cm² x 20 cm²
3
V= 350 cm
3
V= 116.66 cm³
1. Obtén el volumen de las siguientes pirámides.
Pirámide cuadrangular
Área de la base
Volumen
V= ab x h
3
Lado : 9 cm
Altura del cuerpo: 13 cm
Pirámide triangular
Área de la base
Volumen
V= ab x h
3
Base: 15 cm
Altura: 21 cm
Altura del cuerpo: 33 cm
Obtén el volumen de los siguientes pirámides.
Pirámide rectangular
Área de la base
Volumen
V= ab x h
3
13 cm
6 cm
Pirámide pentagonal
Área de la base
Volumen
V= ab x h
3
Base L: 10 cm
Apotema: 8cm
Altura del cuerpo: 25 cm
Pirámide hexagonal
Área de la base
Volumen
V= ab x h
3
Base L : 14 cm
Apotema: 10 cm
Altura del cuerpo: 30 cm
Cálculo mental
Ejercita el cálculo mental hasta con nueve cantidades, alternado sumas, restas,
multiplicaciones y divisiones.
1.
26+ 24, entre 5, x 8 + 40 + 20 – 130 x 7 + 24 + 30 =
2.
48 entre 8, x 9 + 12, entre 6, x 4 + 30, entre 2 + 8, entre 9 =
3.
15 + 27, entre 7, x 9 – 30, entre 6, entre 2, x 8 + 32 =
4.
34 + 12, entre 2, + 15, entre 2, + 11, entre 5, x 9 + 12 =
5.
34 + 12 + 14, entre 15, x 8 + 12, entre 4, x 7 + 20 – 60 =
6.
40 + 35, entre 5, x 3, entre 9, x 8 + 30, entre 10, x 9 + 20 =
7.
25 + 15, entre 8, x 7 + 25, entre 10, x 7 + 40 – 70, entre 4 =
8.
13 + 15, entre 7, x 8 + 20, entre 2, entre 2, - 9 x 8 + 15 + 12 =
9.
28 – 12, entre 4, x 9 + 14, entre 5, x 9 – 60, entre 6, x 8 =
10. 12 + 46 – 30, entre 2, entre 7, x 8 + 30, entre 2, + 15, + 15 =
CÁLCULO MENTAL
Al cuadrado
+23
÷5
÷2
÷8
+20
÷3
Al cuadrado
+15
-50
+14
÷3
3
Al cubo
Al cuadrado
4
Raíz cuadrada
Al cuadrado
-62
+59
49
Raíz cuadrada
64
÷4
Al cubo
+20
2
-18
÷10
CÁLCULO MENTAL
Raíz cuadrada
+9
+50
-38
-20
÷9
81
Al cubo
-90
÷5
Al cuadrado
+15
÷8
5
Raíz cuadrada
x10
÷4
-20
+12
÷7
x9
Al cuadrado
x9
144
Al cuadrado
3
+12
÷3
CÁLCULO MENTAL
Al cubo
-90
÷5
Al cuadrado
+15
÷8
Al cuadrado
-60
÷10
Al cubo
81
-25
-19
Al cuadrado
+6
÷7
x10
-75
54
Al cuadrado
-85
÷5
8
Raíz cuadrada
225
-25
÷5
Al cuadrado
1. 5 playeras cuestan $45.90. ¿Cuánto se deberá pagar para comprar 22
playeras?
Datos
Operaciones
Resultado
2. 8 gorras tienen un costo de $165 pesos, ¿Cuánto se deberá pagar por
comprar 34 gorras?
Datos
Operaciones
Resultado
3. Tres guitarras tienen un costo de $1050 pesos, ¿Cuánto se deberá
pagar para comprar 10 guitarras?
Datos
Operaciones
Resultado
1. Maricela cocinará arroz para la comida de hoy. Si en su despensa
tiene 8/9 de kg de arroz y utilizará 3/6 de kg ¿Qué cantidad de arroz
le sobrará?
2. Datos
Operaciones
Resultado
2. Me dan una rebanada de 3/5 de un melón y después otra rebanada
de 2/6 de ese melón ¿Cuánto melón me comí?
Datos
Operaciones
Resultado
3. Se sabe que el 23% de los habitantes de una colonia tienen menos de
10 años. Si la colonia tiene 9 453 habitantes ¿Cuántos habitantes
aproximadamente tienen 10 ó más años?
Datos
Operaciones
Resultado
PIRÁMIDES NUMÉRICAS
13 9
3
10 14 7
5 14 3
16 9 13
15
24 29 23
23 22 20
21 21 25
22 16 20
20 17 19
21 19 12
7 15
17 18 16
PIRÁMIDES NUMÉRICAS
20
17
10
10
4
11
5
2
5
18
9
32
13
32
16
6
6
29
16
9
33
29
16
8
19
8
10
40
20
8
31
34
18
7
10
14
PIRÁMIDES NUMÉRICAS
5 8
8
11
16 7
12 12
9
6
10 8
6
4
11 4
18 15 19 18
PIRÁMIDES NUMÉRICAS
31 36 26 32
25 33 28 37
37 37 29 21
10
2
5
5
5
4
4
2
PIRÁMIDES NUMÉRICAS
10 15
5
3
1
10 8
4
11
7
4
2
7
8
45
20
8
3
6 12
PIRÁMIDES NUMÉRICAS
25
35
16
22
11
4
10 7
54
27
15
14
87
54
9
11 15
9 13 6
Cálculo mental
Resuelve mentalmente las siguientes operaciones y escribe los
resultados.
25 + 24 + 15 =
18 + 14 + 15 =
63 + 10 + 25 =
29 + 11 + 18 =
16 + 14 + 25 =
100 + 50 - 125 =
35 + 15 + 48 =
75 + 50 - 100 =
50 + 18 + 36 =
1000 ÷ 2 X 6 =
97 + 13 + 35 =
600 ÷ 2 X 5 =
1400 ÷ 2 X 4 =
1600 ÷ 200 X 2 =
100 X 7 ÷ 2 =
300 ÷ 60 X 2 =
1. Calcula el área y perímetro de las siguientes figuras.
PERÍMETRO
ÁREA
PERÍMETRO
ÁREA
PERÍMETRO
ÁREA
PERÍMETRO
ÁREA
16 cm
7 cm
7 cm
10 cm
28 cm
21.5 cm
PERÍMETRO
ÁREA
PERÍMETRO
ÁREA
PERÍMETRO
ÁREA
PERÍMETRO
ÁREA
16 cm
8 cm
13 cm
6.5 cm
PERÍMETRO
ÁREA
PERÍMETRO
ÁREA
PERÍMETRO
ÁREA
PERÍMETRO
ÁREA
17 cm
19 cm
34 cm
27 cm
25 cm
19 cm
13 cm
15 cm
9 cm
PERÍMETRO
ÁREA
PERÍMETRO
ÁREA
PERÍMETRO
ÁREA
PERÍMETRO
ÁREA
35 cm
17 cm
28 cm
13 cm
22 cm
10 cm
17 cm
15 cm
1. Un arquitecto quiere construir en un terreno rectangular. El terreno
mide 50 cm de ancho y 30 m de largo y necesita colocar losetas de 2
m por 2m. ¿Cuántas losetas necesita el arquitecto para cubrir todo el
terreno?
DATOS
OPERACIONES
R:_________________________
2. Una persona es la encargada de pintar la orilla de un parque que
tiene una forma hexagonal. Si cada lado mide 16 metros y una
cubeta de pintura alcanza para pintar 4 metros, ¿Cuántas cubetas de
pintura necesita para pintar la orilla del parque?
DATOS
OPERACIONES
R:___________________________
3. En un parque se está construyendo una figura triangular de 3 metros
de base y 24 metros de altura. ¿Cuál es el área de la figura?
DATOS
OPERACIONES
R:_________________________
4. En una sala de cine se van a colocar butacas. La sala de cine mide
20 metros de largo y 20 metros de ancho. Si cada butaca ocupará 6
metros cuadrados, ¿Cuántas butacas caben, si se planea usar el 75%
del espacio?
DATOS
OPERACIONES
R:___________________________
5. Un arquitecto quiere construir una fuente pentagonal. Si cada lado
mide 5 metros y la apotema también mide 5 metros, ¿Cuál será el
área de la fuente?
DATOS
OPERACIONES
R:_________________________
6. Oswaldo está dibujando su cancha de futbol, y quiere saber cuál
será el perímetro del círculo central. Si el círculo central tiene un radio
de 3 metros, ¿Cuál es su perímetro?
DATOS
OPERACIONES
R:___________________________
7. En un terreno rectangular de 720 m² se van a construir cuatro
locales de comida. En el primero se va a ocupar el 25% del terreno, en
el segundo se va a usar el 60% del terreno, en el tercero se va a utilizar
el 10% del terreno, y en el cuarto va a ocupar lo restante, ¿Cuántos
metros cuadrados va a ocupar cada local?
DATOS
OPERACIONES
R:_________________________
8. Una empresa quiere comprar un terreno con la mayor cantidad de
metros cuadrados posibles. Su primera opción es un terreno hexagonal
en donde cada lado mide 17 metros y tiene una apotema de 11
metros. Su segunda opción es un terreno cuadrangular en donde
cada lado mide 23 metros. Su tercera opción es un terreno
rectangular en donde su largo es de 15 metros y su ancho es de 12
metros. ¿Qué terreno debe comprar la empresa?
DATOS
OPERACIONES
R:___________________________
Alumno: _______________________________
Fecha:_________________________________
Tiempo:_______________ cal:_____________
XX + XX =
CL + D =
12 X ____ =24
X+X=
L+L=
12 X ____ = 60
15 X _____ = 75
C + CV =
LXX + VI =
5 X _______ = 45
XIX + XIX =
D+D=
VII + XIII =
8 X ______ = 80
XV + XV =
CI – XXXV =
x6
8
5
9
7
6
x9
x7
x8
Operaciones al minuto
a) 293 + 940 + 948 =_______
b) 483 + 928 + 103 =_______
c) 843 + 839 + 723 = ______
d) 536 + 172 + 732 =_______
e) 392 + 930 + 834 =_______
8 392034
9 849302
7 930218
Tiempo:_______
calificación:_______
6 291023
5 738293
Operaciones al minuto
a) 390 + 30 + 50 =_________
b) 45 + 25 + 950 = ________
c) 450 + 70 + 1330 = ______
d) 49 + 92 + 492 =_________
e) 83 + 93 + 10 = __________
f) 593 + 7 + 94 = __________
987456
x9
958673
x8
495835
x6
Tiempo:_______
calificación:_______
859483
x7
Operaciones al minuto
394589
+456783
849372
+839204
920384
+849302
892539
- 456783
823489
- 156732
744211
- 236783
83024
x9
39458
x8
91031
x7
83029
x6
Tiempo:_______
calificación:_______