Tarea 1 de ANALISIS DE SISTEMAS LINEALES Victor Miranda - Benjamín Fica

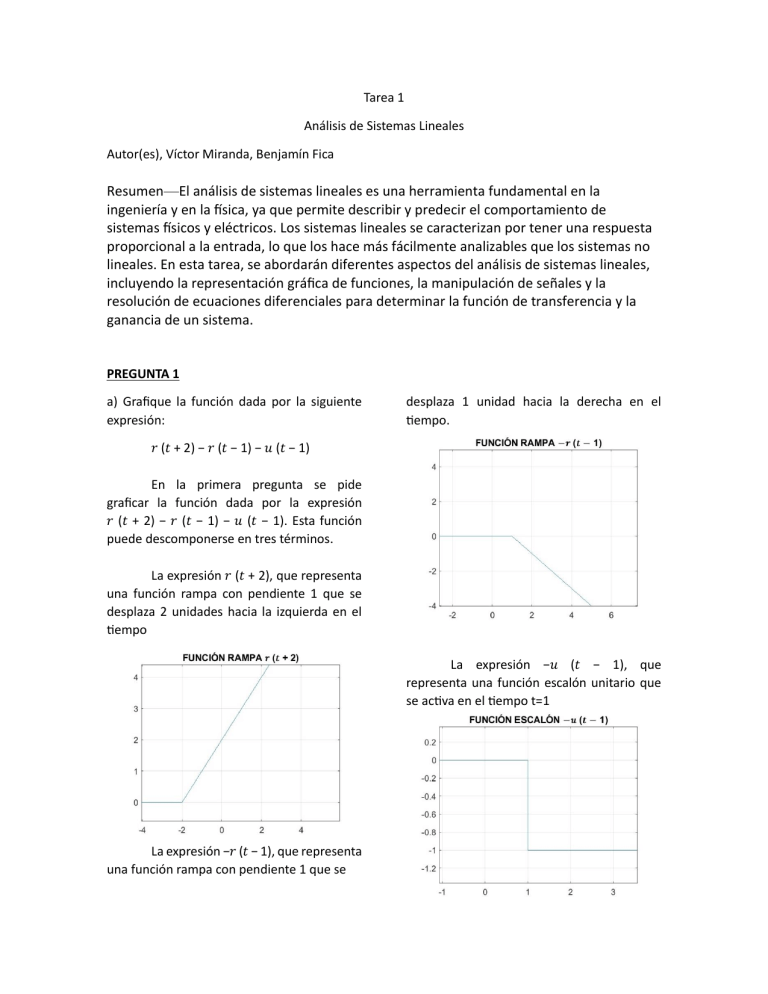
Tarea 1
Análisis de Sistemas Lineales
Autor(es), Víctor Miranda, Benjamín Fica
Resumen—El análisis de sistemas lineales es una herramienta fundamental en la
ingeniería y en la física, ya que permite describir y predecir el comportamiento de
sistemas físicos y eléctricos. Los sistemas lineales se caracterizan por tener una respuesta
proporcional a la entrada, lo que los hace más fácilmente analizables que los sistemas no
lineales. En esta tarea, se abordarán diferentes aspectos del análisis de sistemas lineales,
incluyendo la representación gráfica de funciones, la manipulación de señales y la
resolución de ecuaciones diferenciales para determinar la función de transferencia y la
ganancia de un sistema.
PREGUNTA 1
a) Grafique la función dada por la siguiente
expresión:
desplaza 1 unidad hacia la derecha en el
tiempo.
𝑟 (𝑡 + 2) − 𝑟 (𝑡 − 1) − 𝑢 (𝑡 − 1)
En la primera pregunta se pide
graficar la función dada por la expresión
𝑟 (𝑡 + 2) − 𝑟 (𝑡 − 1) − 𝑢 (𝑡 − 1). Esta función
puede descomponerse en tres términos.
La expresión 𝑟 (𝑡 + 2), que representa
una función rampa con pendiente 1 que se
desplaza 2 unidades hacia la izquierda en el
tiempo
La expresión −𝑢 (𝑡 − 1), que
representa una función escalón unitario que
se activa en el tiempo t=1
La expresión −𝑟 (𝑡 − 1), que representa
una función rampa con pendiente 1 que se
La figura resultante de la suma de
estas tres funciones es una función que se
inicia en t=-2 y se extiende hasta t=2. La
gráfica resultante puede ser construida
utilizando herramientas de software de dibujo
o de cálculo simbólico.
PREGUNTA 2
Para la siguiente función, se pide:
a) La señal quede invertida y su amplitud
quede comprendida entre -3 y 4
1.Como primer paso se crea un
programa en MATLAB tiene como objetivo
crear y graficar una señal modificada a partir
de
una
señal
original
y
varias
transformaciones. Primero, se define el vector
de tiempo "t" que contiene valores desde -5
hasta 5 con un paso de 0.001. Luego, se realiza
la normalización de la señal original mediante
la definición de dos parámetros alfa (alp) y
beta (bet). Alfa se establece en 1/6 y beta en 1/2.
t = (-5:0.001:5)';
%Normalizado de la señal
alp = 1/6;
bet =-1/2;
A continuación, se definen tres
escalones unitarios "U1", "U2" y "U3" que se
utilizarán para construir la señal original "F".
Cada escalón se define como una función que
es 1 para valores de tiempo iguales o mayores
que un valor específico y 0 en cualquier otro
caso. En este caso, U1 se define para valores
de tiempo iguales o mayores que -2, U2 se
define para valores de tiempo iguales o
mayores que 0, y U3 se define para valores de
tiempo iguales o mayores que 2. La señal
original "F" se construye mediante la
combinación de los escalones unitarios con
las operaciones aritméticas necesarias para
obtener la señal deseada
% escalón unitario
U1 = (t>=-2);
U2 = (t>=0);
U3 = (t>=2);
F=((2.*U1)+3)+4.*U2-3.*U3;
SCRIPT COMPLETO
MATLAB
DEL
PROGRAMA
La señal "G" se obtiene al multiplicar
la señal original "F" por el valor de alfa y luego
sumar el valor de beta. En este caso, esto
resulta en la señal original normalizada.
clear all
close all
clc
G= alp*F+bet;
% Definición de la variable
independiente t
t = (-5:0.001:5)';
% Normalización de la señal
alp = 1/6;
bet = -1/2;
% Ajuste de amplitud y reflexión de
la señal
alp2 = -7;
bet2 = 4;
% Definición de los escalones
unitarios
U1 = (t >= -2);
U2 = (t >= 0);
U3 = (t >= 2);
Finalmente, la señal "H" se obtiene al
multiplicar la señal "G" por el valor de alfa2 y
luego sumar el valor de beta2. En este caso,
esto resulta en la inversión de la señal original
y el desplazamiento de la señal.
alp2 = -7;
bet2 = 4;
H=alp2.*G+bet2
% Definición de la función original
F = ((2 .* U1) + 3) + 4 .* U2 - 3 .*
U3;
% Normalización de la señal
G = alp * F + bet;
% Aplicación de la transformación
lineal para ajustar la amplitud y
reflexionar la señal
H = alp2 .* G + bet2;
% Gráfica de la señal resultante
plot(t, H)
% Definición de los límites de la
gráfica
axis([-5; 5; -9; 5]);
% Habilitación de la cuadrícula en
la gráfica
grid on
b) El tiempo de la señal quede comprendido
entre -15 y 15
De las mismas variables para la
transformación de la señal. alp y bet son
utilizados para normalizar la señal entre un
rango específico. alp2 y bet2 se utilizan para
otra transformación de la señal. a es un factor
de amplificación del tiempo para que la señal
quede comprendida entre -15 y 15.
bet
=
-1/2;
%
Factor
Normalización de la señal
de
alp2 = -7; % Factor de amplificación
bet2 = 4; % Factor de desplazamiento
a = 1/7.5; % Factor de amplificación
del tiempo
% Escalones unitarios
U1 = (a*t >= -2); % Escalón unitario
desplazado hacia la izquierda
U2 = (a*t >= 0); % Escalón unitario
en t=0
U3 = (a*t >= 2); % Escalón unitario
desplazado hacia la derecha
%
Función
resultante
de
Normalización de la señal
F = ((2.*U1)+3)+4.*U2-3.*U3;
SCRIPT COMPLETO
MATLAB
DEL
PROGRAMA
clear all
% Limpia las variables
guardadas en la memoria
close all
% Cierra todas las
ventanas de figuras previamente
abiertas
clc
% Limpia la ventana
de comandos
t = (-20:0.0001:20)’; % Vector de
tiempo de -20 a 20 con incrementos
de 0.0001
% Normalización de la señal
alp = 1/6; % Factor de Normalización
de la señal
la
%
Transformación
de
la
original con normalización
G = alp*F+bet;
señal
%
Transformación
normalizada
H = alp2.*G+bet2;
señal
de
la
% Gráfica de la señal resultante
plot(t, H)
axis([-18 18 -5 6]) % Establece los
límites de los ejes x e y de la
gráfica
grid on
% Habilita la
cuadrícula en la gráfica
PREGUNTA 3
𝐻(𝑆) =
Pregunta 3
Para el circuito eléctrico RLC de la Figura N°1.
𝑉𝑐 (𝑆)
𝑉𝑖𝑛 (𝑆)
1
=
2
𝐿𝐶𝑆 + 𝑅𝐶𝑆 + 1
c) Determine la ganancia dc del sistema,
si 𝐿 =10𝑚𝐻, 𝑅 = 100Ω, 𝐶 = 10𝜇𝐹.
Para calcular la ganancia DC del sistema, debemos
encontrar la función de transferencia en DC. La
función de transferencia para este circuito es:
Figura N°1.- Cto. RLC serie con capacitor tomado como de salida
a) Determine la ecuación diferencial de 2do orden
en función de 𝑣𝑐(𝑡), que lo representa:
A continuación, se procede a un LVK en el cto. de la
fuente:
𝑒𝑖𝑛 (𝑡) = 𝑣𝑙 (𝑡) + 𝑣𝑅 (𝑡) + 𝑣𝑐 (𝑡)
Para 𝑒𝑖𝑛 (𝑡) = 𝑣𝑖𝑛 (𝑡)
𝑣𝑖𝑛 (𝑡) = 𝑣𝑙 (𝑡) + 𝑣𝑅 (𝑡) + 𝑣𝑐 (𝑡)
𝑑𝑖(𝑡)
𝑣𝑖𝑛(𝑡) = 𝐿
+ 𝑅𝑖(𝑡) + 1𝐶∫ 𝑖(𝑡)𝑑𝑡
𝑑𝑡
Se sabe que:
1
𝑣𝑐 (𝑡) = ∫ 𝑖(𝑡)𝑑𝑡
𝐶
𝑑
𝑑
(𝑡))
( 𝐶𝑣𝑐
= (∫ 𝑖(𝑡)𝑑𝑡)
𝑑𝑡
𝑑𝑡
𝑑𝑣𝑐 (𝑡)
𝐶
= 𝑖(𝑡)
𝑑𝑡
Reemplazando 𝑖(𝑡):
𝑑𝑑𝑣𝑐
𝑑𝑣𝑐 (𝑡) 1
𝑑𝑣𝑐 (𝑡)
𝑣𝑖𝑛(𝑡) = 𝐿𝐶
+ 𝑅𝐶
+ ∫𝐶
𝑑𝑡
𝑑𝑡𝑑𝑡
𝑑𝑡
𝐶
𝑑𝑡
De esta forma se obtiene la ecuación diferencial de
2do orden en función de 𝑣𝑐(𝑡):
𝑣𝑐 (𝑡) = −𝐿𝐶
𝑑2 𝑣𝑐 (𝑡)
𝑑𝑣𝑐 (𝑡)
− 𝑅𝐶
+ 𝑣𝑖𝑛(𝑡)
𝑑𝑡 2
𝑑𝑡
b) Determine la función de transferencia 𝑣𝑐(𝑆)/𝑢(𝑆)
con condiciones iniciales nulas:
𝑣𝑖𝑛(𝑡) = 𝐿𝐶
𝑑 2 𝑣𝑐 (𝑡)
𝑑𝑣𝑐 (𝑡)
+ 𝑅𝐶
+ 𝑣𝑐 (𝑡) / 𝐿𝐴𝑃𝐿𝐴𝐶𝐸()
𝑑𝑡 2
𝑑𝑡
𝑉𝑖𝑛 (𝑆) = 𝐿𝐶[𝑆 2 𝑉𝑐 − 𝑆𝑉𝑐 (0) −
𝑑𝑣𝑐 (0)
] + 𝑅𝐶[𝑆𝑉𝑐 (𝑆) − 𝑣𝑐 (0)] + 𝑉𝑐 (𝑆)
𝑑𝑡
𝑉𝑖𝑛 (𝑆) = 𝐿𝐶𝑆 2 𝑉𝑐 (𝑆) + 𝑅𝐶𝑆𝑉𝑐 (𝑆) + 𝑉𝑐 (𝑆)
𝑉𝑖𝑛 (𝑆) = 𝑉𝑐 (𝑆)(𝐿𝐶𝑆 2 + 𝑅𝐶𝑆 + 1)
𝑉𝑐 (𝑆) =
𝑉𝑖𝑛 (𝑆)
+ 𝑅𝐶𝑆 + 1
𝐿𝐶𝑆 2
Para la función de transferencia queda como:
𝐻(𝑆) =
𝑉𝑐 (𝑆)
𝑉𝑖𝑛 (𝑆)
1
=
𝐿𝐶𝑆2 + 𝑅𝐶𝑆 + 1
Por ende, se evalúa la función de transferencia
cuando 𝑆 tiende a 0, en resumidas cuentas, para
encontrar la ganancia DC, simplemente hacemos S=0
en la función de transferencia:
lim 𝑓(𝑡) = lim 𝑆 ∗ 𝐻(𝑆) ∗ 𝑈(𝑆)
𝑡→∞
𝑆→0
lim 𝑆 ∗
𝑆→0
lim
1
2
𝐿𝐶𝑆 + 𝑅𝐶𝑆 + 1
1
2
𝑆→0 𝐿𝐶(0) + 𝑅𝐶(0) + 1
=
∗
1
𝑆
1
+= 1
1
La ganancia DC del sistema queda como:
lim
1
2
𝑆→0 𝐿𝐶(0) + 𝑅𝐶(0) + 1
=
1
+= 1
1
Por lo tanto, la ganancia DC del sistema es
de 1. Esto significa que la señal de entrada
DC se amplifica por una cantidad unitaria,
lo que equivale a que la señal de salida DC
es igual a la señal de entrada DC.