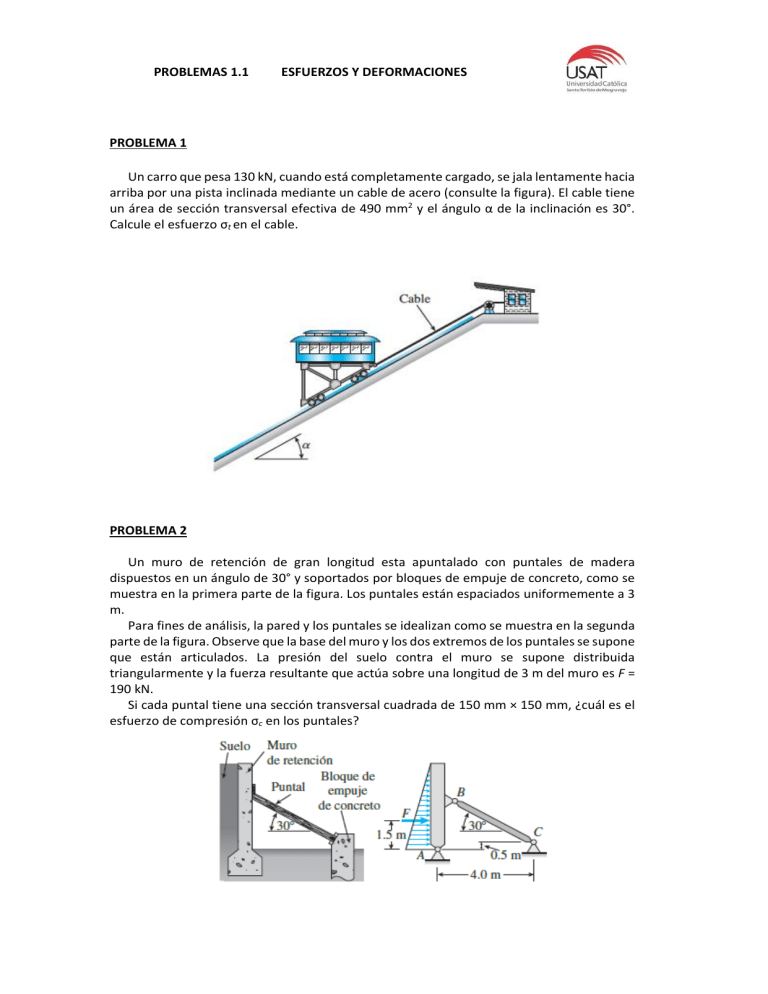
PROBLEMAS 1.1 ESFUERZOS Y DEFORMACIONES PROBLEMA 1 Un carro que pesa 130 kN, cuando está completamente cargado, se jala lentamente hacia arriba por una pista inclinada mediante un cable de acero (consulte la figura). El cable tiene un área de sección transversal efectiva de 490 mm2 y el ángulo α de la inclinación es 30°. Calcule el esfuerzo σt en el cable. PROBLEMA 2 Un muro de retención de gran longitud esta apuntalado con puntales de madera dispuestos en un ángulo de 30° y soportados por bloques de empuje de concreto, como se muestra en la primera parte de la figura. Los puntales están espaciados uniformemente a 3 m. Para fines de análisis, la pared y los puntales se idealizan como se muestra en la segunda parte de la figura. Observe que la base del muro y los dos extremos de los puntales se supone que están articulados. La presión del suelo contra el muro se supone distribuida triangularmente y la fuerza resultante que actúa sobre una longitud de 3 m del muro es F = 190 kN. Si cada puntal tiene una sección transversal cuadrada de 150 mm × 150 mm, ¿cuál es el esfuerzo de compresión σc en los puntales? PROBLEMA 3 Una puerta trasera de una camioneta soporta una caja (Mc = 68 kg), como se muestra en la figura siguiente. La puerta pesa Mt = 27 kg y está soportada por dos cables (solo se muestra uno en la figura). Cada cable tiene un área transversal efectiva Ae= 11.0 mm2). (a) Encuentre la fuerza de tensión T y el esfuerzo normal σ en cada cable. PROBLEMA 4 Para la armadura mostrada en la figura, determinar la tensión en los miembros AC y BD. El área de la sección transversal de cada uno es de 900 mm2. PROBLEMA 5 En la figura se muestra parte del tren de aterrizaje de una avioneta. Determine el esfuerzo de compresión en el tornapunta AB producido al aterrizar por una reacción del terreno R = 20 kN. AB forma un ángulo de 53.1° con BC. PROBLEMA 6 Cada uno de los cuatro eslabones verticales tiene una sección transversal rectangular uniforme de 8x36 mm y cada uno de los cuatro pasadores tiene un diámetro de 16 mm. Determine el valor máximo del esfuerzo normal promedio en los eslabones que conectan a) los puntos B y D, b) los puntos C y E. PROBLEMA 7 Dos marcas de calibración se colocan a una separación exacta de 250 mm en una varilla de aluminio que tiene un diámetro de 12 mm. Si se sabe que al aplicar una carga axial de 6000 N sobre la varilla, la distancia entre las marcas de calibración es de 250.18 mm, determine el módulo de elasticidad del aluminio usado en la varilla. PROBLEMA 8 Un alambre de acero de 60 m de largo se sujeta a una carga de tensión de 6 kN. Si se sabe que E = 200 GPa y que la longitud del alambre aumenta 48 mm, determine a) el diámetro del alambre, b) el esfuerzo normal correspondiente. PROBLEMA 9 Para la armadura de acero (E = 200 GPa) y la carga mostradas en la figura, determine las deformaciones de los elementos AB y AD, si se sabe que sus respectivas áreas de sección transversal son de 2400 mm2 y 1800 mm2. PROBLEMA 10 Cada uno de los cuatro eslabones verticales que conectan los dos elementos horizontales que se muestran en la figura está hecho de aluminio (E= 70 GPa) y tiene una sección transversal rectangular uniforme de 10 x 40 mm. Para la carga mostrada, determine la deflexión de a) el punto E, b) el punto F y c) el punto G. Soluciones 1) σt = 132.65 MPa 2) σC = 5.21 MPa (C) 3) T= 819 N, σ =74.5 MPa 4) σAC = 59.26 MPa (T), σBD = 74.10 MPa (C) 5) σAB = 65.7 MPa 6) a) 56.4 MPa b) - 21.7 MPa 7) E = 73.7 GPa 8) a) 6.91 mm b) 160.0 MPa 9) δAB = -2.11 mm, 10) a) 80.4 μm ↑ δAD = 2.03 mm. b) 209 μm ↓ c) 390 μm ↓ PROBLEMAS 1.2 RELACIÓN DE POISSON PROBLEMA 1 Una varilla con 20 mm de diámetro, hecha de un plástico experimental, se somete a una fuerza de tensión con una magnitud P = 6 kN. Puesto que se observa un alargamiento de 14 mm y una disminución en diámetro de 0.85 mm en una longitud calibrada de 150 mm, determine el módulo de elasticidad, el módulo de rigidez y la relación de Poisson para el material. PROBLEMA 2 El cambio de diámetro de un perno grande de acero se mide cuidadosamente mientras se aprieta se aprieta la tuerca. Si se sabe que E = 200 GPa y ν = 0.29, determine la fuerza interna en el perno, si se observa que el diámetro disminuye 13 μm. PROBLEMA 3 Una tela utilizada en estructuras infladas con aire se sujeta a una carga biaxial que resulta en esfuerzos normales σx = 120 MPa y σz = 160 MPa. Si se sabe que las propiedades de la tela pueden aproximarse a E = 87 GPa y ν =0.34, determine el cambio en longitud de a) el lado AB, b) el lado BC, c) la diagonal AC. PROBLEMA 4 El bloque mostrado en la figura es de una aleación de magnesio para la que E = 45 GPa y υ = 0.35. Si se sabe que σx = -180 MPa, determine a) la magnitud de σy para la cual el cambio en la altura del bloque será cero, b) el cambio correspondiente en el área ABCD, c) el cambio correspondiente en el volumen del bloque. PROBLEMA 5 El bloque de plástico mostrado en la figura está adherido a un soporte rígido y a una placa vertical a la que se aplica una fuerza P de 240 kN. Si se sabe que para el plástico usado G = 1050 MPa, determine la deflexión de la placa. Figura problemas 5 y 6 PROBLEMA 6 ¿Cuál es la carga P que debe aplicarse a la placa del problema anterior para producir una deflexión de 1.5 mm? PROBLEMA 7 Un soporte elastomérico (G = 0.9 MPa) se emplea para apoyar una viga de un puente, como se muestra en la figura, para suministrar flexibilidad durante terremotos. La viga no debe desplazarse más de 10 mm cuando una carga lateral de 22 kN sea aplicada como se muestra en la figura. Si se sabe que el máximo esfuerzo tangencial de corte permisible es de 420 kPa, determine a) la dimensión b mínima permisible, b) el mínimo grosor a requerido. Figura problemas 7 y 8 PROBLEMA 8 Para el apoyo elastométrico de la figura con b= 220 mm y a = 30 mm, determine el módulo de cortante G y el esfuerzo cortante τ para una carga lateral máxima P = 19 kN y un desplazamiento máximo δ = 12 mm. PROBLEMA 9 a) Para la carga axial mostrada en la figura, determine el cambio en altura y el cambio en volumen del cilindro de latón mostrado. b) Resuelva el inciso a), con el supuesto de que la carga es hidrostática con σx = σy = σz = -70 MPa Soluciones: 1) E = 205 MPa; ν = 0.455; G = 70.3 MPa 2) 422 kN 3) a) 0.0754 mm b) 0.1028 mm c) 0.1220 mm 4) a) -63.0 MPa b) -4.06 mm2 c) -162 mm3 5) 1.19 mm 6) 302 kN 7) a) 262 mm b) 21.4 mm 8) G = 1.080 MPa; τ = 431 kPa. 9) a) Δh = -0.0746 mm; ΔV = -143 mm3; b) Δh = -0.0306 mm; ΔV = -521 mm3 PROBLEMAS 1.3 PASADORES. DIAGRAMA TENSIÓN DEFORMACIÓN PROBLEMA 1 Los elementos de madera A y B deben unirse mediante láminas de madera contrachapada que se pegarán por completo sobre las superficies en contacto. Como parte del diseño de la junta y puesto que el claro entre los extremos de los elementos será de 6 mm, determine la longitud mínima permisible L, si el esfuerzo tangencial promedio en el pegamento no debe exceder 700 kPa. PROBLEMA 2 Para el ensamble y la carga del elemento que aparece en la figura determine a) el esfuerzo tangencial promedio en el pasador en B. Cada uno de los cuatro eslabones verticales tiene una sección transversal rectangular uniforme de 8 x 36 mm y cada uno de los cuatro pasadores tiene un diámetro de 16 mm. PROBLEMA 3 La armadura de dos barras ABC que se muestra en la figura tiene soportes articulados en los puntos A y C, que están separados 2.0 m. Los elementos AB y BC son barras de acero, interconectadas por un pasador en el nodo B. La longitud de la barra BC es de 3.0 m. Un anuncio que pesa 5.4 kN está suspendido de la barra BC en los puntos D y E, que están ubicados a 0.8 m y 0.4 m, respectivamente, de los extremos de la barra. Determine el área de la sección transversal necesaria de la barra AB y el diámetro necesario del pasador en el soporte C si los esfuerzos en tracción y cortante son 125 MPa y 45 MPa, respectivamente. (Nota: los pasadores en los soportes están en cortante doble. Además, no tome en cuenta los pesos de los elementos AB y BC). PROBLEMA 4 La armadura plana de acero en la figura está sometida a tres fuerzas P, cada una de 490 kN. Cada uno de los elementos de la armadura tiene un área de sección transversal de 3900 mm2 y están conectados mediante pasador que tienen un diámetro dp = 18 mm. Cada uno de los elementos AC y BC consiste de una barra con espesor tAC = tBC = 19 mm. El elemento AB está compuesto de dos barras [consulte la parte (b) de la figura] que tienen, cada una, un espesor tAB/2 = 10 mm y una longitud L = 3 m. El apoyo de rodillo en B está compuesto de dos placas de soporte que tienen, cada una un espesor tsp/2 = 12 mm. a) Determine las reacciones de soporte en los nodos A y B, y las fuerzas en los elementos AB, BC y AC. b) Calcule el esfuerzo tangencial promedio mayor τp,máx en el pasador en el nodo B, ignore la fricción entre los elementos; consulte las partes (b) y (c) de la figura donde se muestran las vistas en corte del nodo. PROBLEMA 5 Los elementos de soporte de una armadura que sostiene un techo están conectados a una placa de unión de 26 mm de espesor mediante un pasador con un diámetro de 22 mm, como se muestra en la figura siguientes. Cada una de las dos placas extremas en los elementos de la armadura tiene un espesor de 14 mm. a) Si la carga P = 80 kN, ¿cuál el esfuerzo de soporte mayor que actúa sobre el pasador? b) Si el esfuerzo tangencial último para el pasador es de 190 MPa, ¿cuál es la fuerza Púlt que se requiere para que el pasador falle en cortante? (No tenga en cuenta la fricción entre las placas). PROBLEMA 6 La escalera inclinada AB soporta a un pintor de casas (82 kg) en C y el peso propio (q = 36 N/m) de la escalera. Cada riel de la escalera (tr = 4 mm) está soportado por una zapata (ts = 5 mm) que está sujeta al riel de la escalera mediante un perno don diámetro d = 8 mm. a) Encuentre las reacciones de soporte en A y B. b) Encuentre la fuerza resultante en el perno de la zapata en A. c) Encuentre el esfuerzo tangencial máxima promedio (τ). PROBLEMA 7 Un pasador de 6 mm de diámetro se utiliza en la conexión C del pedal que se muestra en la figura. Si se sabe que P = 500 N, determine la tensión tangencial promedio en el pasador. PROBLEMA 8 Una barra circular de una aleación de magnesio tiene una longitud de 750 mm. El diagrama esfuerzo-deformación unitaria para el material se muestra en la figura. La barra se carga en tracción hasta obtener un alargamiento de 6.0 mm y luego se quita la carga. a) ¿Cuál es la deformación permanente de la barra? b) Si la barra se vuelve a cargar, ¿cuál es el límite de proporcionalidad? PROBLEMA 9 En la figura se muestra el diagrama esfuerzo-deformación para una aleación de aluminio utilizada en la fabricación de partes de aeronaves. Si una probeta de este material se esfuerza hasta 600 MPa, determine la deformación permanente que queda en la probeta cuando ésta se libera de la carga. Soluciones 1) 292 mm 2) 80.8 MPa. 3) AAB = 44.1 mm2, d = 8.54 mm 4) (a) Ax = 0, By = 0, Ay 490 = kN; FBC = 0, FAB = 490 kN, FAC = 693 kN (b) τp = 963 MPa 5) τ = 105.23 MPa; Púlt = 144.45 kN 6) (a) Ax = 254.6 N, Ay = 1072 N, Bx = 254.6 N (b) Aresultante = 1101.8 N MPa 7) 23.0 MPa. 8) a) 3 mm; b) 180 MPa 9) 0.0015 (c) τ = 5.48 PROBLEMAS 1.4 ESFUERZO ÚLTIMO Y ESFUERZO ADMISIBLE PROBLEMA 1 Se aplican dos fuerzas a la ménsula BCD como se muestra en la figura. A) Sabiendo que la varilla de control AB será de acero con un esfuerzo normal último de 600 MPa, determine el diámetro de la varilla utilizando un factor de seguridad de 3.3. b) El perno en C será de un acero con un esfuerzo tangencial último al corte de 350 MPa. Encuentre el diámetro del perno C tomando en cuenta que el factor de seguridad con respecto al corte también será de 3.3 PROBLEMA 2 Un aro de acero ABCD de 1.2 m de largo y 10 mm de diámetro se coloca alrededor de una varilla de aluminio AC de 24 mm de diámetro como se muestra en la figura. Los cables BE y DF, cada uno de 12 mm de diámetro, se utilizan para aplicar la carga Q. Si se sabe que la resistencia última del acero empleado para el aro y los cables es de 480 MPa, y que la resistencia última del aluminio usado para la varilla es de 260 MPa, determine la máxima carga Q que puede aplicarse si se desea obtener un factor de seguridad global de 3. PROBLEMA 3 El elemento ABC, soportado por un pasador y una ménsula en C y un cable BD, se diseñó para soportar una carga P de 16 kN como se muestra en la figura. Si se sabe que la carga última para el cable BD es de 100 kN, determine el factor de seguridad respecto a la falla del cable. PROBLEMA 4 Los dos elementos de madera que se muestran en la figura, soportan una carga de 16 kN y se encuentran unidos mediante láminas de madera contrachapada pegadas completamente a las superficies de contacto. La tensión de cortante última del pegamento es de 2.5 MPa y la separación entre los elementos es de 6 mm. Determine la longitud L requerida para cada lámina si debe lograrse un factor de seguridad de 2.75. Figuras problemas 4 y 5 PROBLEMA 5 Para el ensamble y la carga de la figura, determine el factor de seguridad si la longitud de cada lámina es L = 180 mm. Soluciones 1) 16.74 mm; 20 mm 2) 15.08 kN 3) 3.45 4) 146.8 mm 5) 3.4








