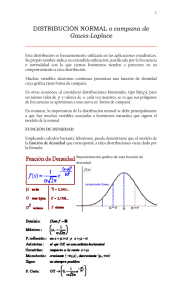
CUN DEPARTAMENTO DE CIENCIAS BASICAS ESTADISTICA DE LA PROBABILIDAD GUIA N º4 PROFESOR: FREDY RIOS DISTRIBUCION DE PROBABILIDAD NORMAL INTRODUCCIÓN En este guía se continúa con el estudio de las distribuciones de probabilidad, examinando una distribución de probabilidad continua muy importante: la distribución de probabilidad normal. Como se indicó en la guía anterior, una variable aleatoria continua es la que puede tomar un número infinito de valores dentro de un intervalo. Generalmente, es el resultado de medir algo, como el peso de una persona. El peso puede ser 162.0 libras (lb), 162.1 lb, 162.12 lb, etc. Otras variables aleatorias continuas son el tiempo de vida de las baterías tipo alcalino, el volumen de un contenedor de embarque y el peso de las impurezas en un lingote de acero. Las distribuciones de probabilidad de las expectativas de vida de algunos productos, como son baterías, neumáticos y focos (o lámparas), tienden a seguir un patrón “normal”. Lo mismo sucede con los pesos de las cajas de cereal, la longitud de rollos de aluminio y otras variables que se miden con una escala continua. La familia de distribuciones de probabilidad normal La distribución de probabilidad normal y su correspondiente curva normal tienen las siguientes características: 1. La curva normal es acampanada y presenta un solo pico en el centro de la distribución. La media aritmética, la mediana y la moda de la distribución son iguales y están localizadas en el pico. De esta forma, la mitad del área bajo la curva se encuentra por arriba de este punto central, y la otra mitad por abajo. 2. La distribución de probabilidad normal es simétrica con respecto a su media. Si se corta la curva normal verticalmente en este valor central, ambas mitades serán como imágenes en el espejo. 3. La curva normal decrece uniformemente en ambas direcciones a partir del valor central. Es asintótica, esto significa que la curva se acerca cada vez más al ele X, pero en realidad nunca llega a tocarlo. Esto es, los puntos extremos de la curva se extienden indefinidamente en ambas direcciones. Estas características se muestran gráficamente en el diagrama 1. Grafica 1. Características de una distribución normal. No existe sólo una distribución de probabilidad normal, sino que hay una familia” de ellas. Existe una distribución de probabilidad normal para los años de servicio de los empleados de la planta de Camden, en la que la media es 20 (años) y la desviación es 3.1 (años) Existe otra distribución de probabilidad normal de los años de servicio en la planta de Dunkirk, en la cual μ= 20 y σ = 3.9. En el diagrama 2 se ilustran tres distribuciones norma donde las medias son iguales, pero las desviaciones estándar son diferentes. Medias iguales, desviaciones estándar distintas Diagrama 2: distribución de probabilidad normal con medias iguales, pero desviaCiones estándar diferente. Medias diferentes estándares iguales Diagrama 3: distribución de probabilidad normal con medias diferentes, pero desviaciones estándar. Diferentes, desviaciones estándar iguales Medias En el diagrama 3 se muestra la distribución de los pesos de tres cereales diferentes. Los pesos están distribuidos en forma normal, con medias diferentes, pero desviaciones estándar idénticas. Por último, en el diagrama 4 se muestran tres distribuciones normales con medias y desviaciones estándar diferentes. Estas distribuciones muestran a distribución de la resistencia a la tensión medida en libras por pulgada cuadrada (lb/pulg2)[psi] de tres tipos de cables. Diagrama 4. Distribución de probabilidad normal con medias y desviación estándar diferente Distribución de probabilidad normal estándar Hay una familia de distribuciones normales. Cada distribución puede tener una media (μ) o desviación estándar (σ) diferentes. Por tanto, el número de distribuciones normales es ilimitado. Seria físicamente imposible proporcionar una tabla de probabilidades (como para las distribuciones binomial y de Poisson) para cada combinación de μ y σ. Por fortuna se puede utilizar, en todos los casos en los que la distribución normal es aplicable, un miembro de la familia de distribuciones normales que tiene una media 0 y una desviación estándar 1, denominado distribución normal estándar. Cualquier distribución normal puede convertirse en la “distribución normal estándar” restando la media a cada observación, y dividiendo entre la desviación estándar. Primero se convierte, ose estandariza, la distribución que se tiene, en la distribución normal estándar utilizando un valor z(también denominado, puntuación z, valor estadístico, desviación normal estándar, o simplemente desviación norma). Valor z Diferencia entre un valor elegido, denotado por X, y la media μ, dividida entre a desviación estándar, σ. Por tanto, un valor z es la distancia a la media, medida en unidades de la desviación estándar. Expresado en una fórmula: Donde: X: es el valor de cualquier medida u observación específica. μ : es a media de la distribución. σ : es la desviación estándar de la distribución. Como se observa en la definición anterior, un valor z mide la distancia entre un valor especifico X y la media aritmética, en unidades de desviación estándar Al determinar el valor z mediante la fórmula 1, se puede obtener el área o la probabilidad bajo cualquier curva normal, recurriendo al apéndice D. Para explicar lo anterior, supóngase que el valor calculado para z es 1.91. ¿Cuál es el área bajo a curva normal entre la media y X? En la tabla 7.1 se reproduce una parte del apéndice D. La columna izquierda de la tabla, encabezada con la letra z, se recorre hacia abajo hasta encontrar el 1.9. Después se desplaza horizontalmente hacia la derecha, se lee la probabilidad bajo la columna encabezada con 0.01. La probabilidad es 0.4719. Esto significa que 47.19% del área bajo la curva normal estándar se encuentra entre la media y el valor X de 1.91 desviaciones estándar después de la media. Esta es la probabilidad de que una observación se encuentre entre 0 y 1.91 desviaciones estándar después de la media. Tabla 1 Áreas bajo la curva normal Usos de la distribución normal estándar ¿Cuál es el área bajo la curva entre la media y X para los siguientes valores z? Compruebe sus respuestas con las expresadas. No todos los valores se encuentran en a tabla 1. Deberá utilizar el apéndice D. Ahora se calculará el valor z para una media poblacional μ, una desviación estándar poblacional σ y una X determinada. Ejemplo Los ingresos semanales de supervisores de turno en la industria del vidrio tienen una distribución normal con media $1 000 (dólares), y desviación estándar $100. ¿Cuál es el valor z correspondiente al ingreso de un supervisor que gana $1 100 a la semana? ¿Y para un supervisor que tiene un ingreso semanal de $900? Solución Utilizando la fórmula (1), los valores z para los dos valoras indicados de X ($1 100 y $900) son: El valor z = 1.00 indica que el ingreso semanal de $1 100 se encuentra a una desviación estándar sobre la media; una z = -1.00 indica que el ingreso de $900 se encuentra a una desviación estándar por debajo de la media. Observe que ambos ingresos ($1 100 y $900) están a la misma distancia ($100) de la media. DISTRIBUCION DE PROBABILIDAD BINOMIAL La distribución binomial es una distribución de probabilidad discreta aplicable como modelo para situaciones de toma de decisiones en las que puede suponerse que un proceso de muestreo responde a un proceso de BERNOULLI en el que: - En cada ensayo u observación solo son posibles dos resultados mutuamente excluyentes, llamados éxito y fracaso. Los resultados de la serie de ensayos constituyen eventos independientes La probabilidad de éxito de cada ensayo es indicada por p La probabilidad de fracaso está dada por: q=1-p Formula de la distribución binomial P( x / n, p) n! p x q n x x!(n x)! Para calcular la media y la desviación estándar de un experimento que tenga una distribución Binomial usaremos las siguientes fórmulas: Media o valor esperado. Donde: n = número de ensayos o repeticiones del experimento P = probabilidad de éxito o la probabilidad referente al evento del cual se desea calcular la media que se refiere la media Q = complemento de P Desviación estándar. Ejemplo Si la probabilidad de que el vapor se condense en un tubo de aluminio de cubierta delgada a 10 atm de presión es de 0.40, si se prueban 12 tubos de ese tipo y bajo esas condiciones, determine la probabilidad de que: a) el vapor se condense en 4 de los tubos, b) en más de 2 tubos se condense el vapor, c) el vapor se condense en exactamente 5 tubos. Solución: a) n =12 x = variable que nos define el número de tubos en que el vapor se condensa x = 0, 1, 2, 3,...,12 tubos en el que el vapor se condensa p = p(se condense el vapor en un tubo de Al a 10 atm)= 0.40 q = p(no se condense el vapor en un tubo de Al a 10 atm) = 1-p=0.60 = 0.21284 b) p(X=3, 4, ...,12, n=12, p=0.40) = p(x=3)+p(x=4)+…+p(x=12)= 1-[p(x=0,1,2)]= = 1-[0.002176+0.0174096+0.06385632]= 1- 0.08344192= 0.91656 c) = 0.22703 DISTRIBUCION DE PROBABILIDAD DE POISSON La distribución de Poisson puede usarse para determinar la probabilidad de ocurrencia de un número establecido de eventos cuando estos ocurren en un cuantiuum temporal o espacial. Para la probabilidad de ocurrencia de un número establecido de eventos solo se requiere de un valor: el número medio de eventos a largo plazo en la dimensión temporal o espacial especifica de interés. Para determinar la probabilidad de que ocurran x éxitos por unidad de tiempo, área, o producto, la fórmula a utilizar sería: P( x / ) x x! donde: p(x, ) = probabilidad de que ocurran x éxitos, cuando el número promedio de ocurrencia de ellos es l = media o promedio de éxitos por unidad de tiempo, área o producto e = 2.7182 es una constante x = variable que nos denota el número de éxitos que se desea que ocurra Hay que hacer notar que en esta distribución el número de éxitos que ocurren por unidad de tiempo, área o producto es totalmente al azar y que cada intervalo de tiempo es independiente de otro intervalo dado, así como cada área es independiente de otra área dada y cada producto es independiente de otro producto dado. Ejemplo Si un banco recibe en promedio 6 cheques sin fondo por día, ¿cuáles son las probabilidades de que reciba, a) cuatro cheques sin fondo en un día dado, b) 10 cheques sin fondos en cualquiera de dos días consecutivos? Solución: a) x = variable que nos define el número de cheques sin fondo que llegan al banco en un día cualquiera = 0, 1, 2, 3, ....., etc, etc. = 6 cheques sin fondo por día e = 2.718 b) x= variable que nos define el número de cheques sin fondo que llegan al banco en dos días consecutivos = 0, 1, 2, 3, ......, etc., etc. = 6 x 2 = 12 cheques sin fondo en promedio que llegan al banco en dos días consecutivos Nota: l siempre debe de estar en función de x siempre o dicho de otra forma, debe “hablar” de lo mismo que x. Propiedades del modelo de Poisson Esperanza: E(X) = λ. Varianza: V(X) = λ. DISTRIBUCION DE PROBABILIDAD HIPERGEOMETRICA Es especialmente útil en todos aquellos casos en los que se extraigan muestras o se realicen experiencias repetidas sin devolución del elemento extraído o sin retornar a la situación experimental inicial. Es una distribución fundamental en el estudio de muestras pequeñas de poblaciones pequeñas y en el cálculo de probabilidades de juegos de azar. Tiene grandes aplicaciones en el control de calidad para procesos experimentales en los que no es posible retornar a la situación de partida. Las consideraciones a tener en cuenta en una distribución hipergeométrica: El proceso consta de "n" pruebas, separadas o separables de entre un conjunto de "N" pruebas posibles. Cada una de las pruebas puede dar únicamente dos resultados mutuamente excluyentes. El número de individuos que presentan la característica A (éxito) es "k". En la primera prueba las probabilidades son: P(A)= p y P(A)= q; con p+q=1. En estas condiciones, se define la variable aleatoria X = “nº de éxitos obtenidos”. La función de probabilidad de esta variable sería: La media, varianza y desviación típica de esta distribución vienen dadas por: Ejemplo Supongamos la extracción aleatoria de 8 elementos de un conjunto formado por 40 elementos totales (cartas baraja española) de los cuales 10 son del tipo A (salir oro) y 30 son del tipo complementario (no salir oro). Si realizamos las extracciones sin devolver los elementos extraídos y llamamos X al número de elementos del tipo A (oros obtenidos) que extraemos en las 8 cartas; X seguirá una distribución hipergeométrica de parámetros 40 , 8 , 10/40.H(40,8,0,25). Para calcular la probabilidad de obtener 4 oros: