Guía de Aprendizaje Física 10: Movimiento en una Dimensión
Anuncio

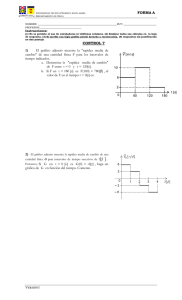
GUÍA DE APRENDIZAJE FISICA – 10 COLEGIO CIUDADELA EDUCATIVA DE BOSA INSTITUCIÓN EDUCATIVA DISTRITAL DESEMPEÑO/DIMENSIÓN Determina la relación de proporcionalidad que existe entre tiempo y distancia al desplazarse cierto cuerpo en una dimensión y genera solución a problemas sobre este tema. PREGUNTA PROBLEMATIZADORA: ¿Cuál es la diferencia entre velocidad y aceleración de un cuerpo? TÓPICOS GENERATIVOS: Movimiento en una dimensión: Distancia, tiempo y velocidad constante. Gráficas de velocidad contra tiempo. MU. MUC. Caída libre. FÍSICA: LA CIENCIA BÁSICA Lic. EVIDELIO LOPEZ S. Galileo Galilei, Isaac Newton y Albert Einstein La física es más que una parte de las ciencias naturales. Es la ciencia básica. Es acerca de la naturaleza de cosas básicas como el movimiento, las fuerzas, la energía, la materia, el calor, el sonido, la luz y la estructura de los átomos. La química explica cómo se acomoda la materia entre sí, cómo se combinan los átomos para formar moléculas, y cómo éstas se combinan para formar los materiales que nos rodean. La biología es más compleja y se ocupa de la materia que está viva. Por lo anterior, en la base de la biología está la química, y en la base de la química está la física. Los conceptos de la física llegan hasta dichas ciencias, que son algo más complicadas. Principales campos de la Física La física cubre una amplia gama de campos. Esta tabla proporciona una breve descripción de los temas tratados en los diferentes ámbitos. Acústica Estudia las propiedades del sonido. Física atómica Estudia la estructura y las propiedades del átomo. Criogenia Estudia el comportamiento de la materia a temperaturas extremadamente bajas. Electromagnetismo Estudia los campos eléctrico y magnético, y las cargas eléctricas que los generan. Física de partículas Se dedica a la investigación de las partículas elementales. Dinámica de fluidos Examina el comportamiento de los líquidos y gases en movimiento. Geofísica Aplicación de la física al estudio de la Tierra. Incluye los campos de la hidrología, la meteorología, la oceanografía, la sismología y la vulcanología. Física matemática Estudia las matemáticas en relación con los fenómenos naturales. Mecánica Estudia el movimiento de los objetos materiales sometidos a la acción de fuerzas. Física molecular Estudia las propiedades y estructura de las moléculas. Física nuclear Analiza las propiedades y estructura del núcleo atómico, las reacciones nucleares y su aplicación. Óptica Estudia la propagación y el comportamiento de la luz. Física del plasma Estudia el comportamiento de los gases altamente ionizados (con carga eléctrica). Física cuántica Estudia el comportamiento de sistemas extremadamente pequeños y la cuantización de la energía. Física de la materia Estudia las propiedades físicas de los sólidos y los líquidos. condensada Mecánica estadística Aplica principios estadísticos para predecir y describir el comportamiento de sistemas compuestos de múltiples partículas. Termodinámica Estudia el calor y la conversión de la energía de una forma a otra. Conceptos Básicos MAGNITUD: Es todo aquello que se puede medir. En la Física tendremos en cuenta la longitud, la masa, el tiempo, velocidad, aceleración, fuerza. etc. MEDIR: Es comparar una magnitud con otra que se ha elegido como patrón de medida. Ejemplo: el patrón de medida de la longitud es el metro, el de la masa es el kilogramo, el del tiempo es el segundo, el de la temperatura es el ºC o °K. etc. MEDICIÓN DIRECTA E INDIRECTA: Una medición es directa cuando se hace mediante un proceso visual y con el patrón de medida. Es indirecta si se hace con el uso de aparatos específicos o por cálculos matemáticos. MAGNITUDES FUNDAMENTALES: En la mecánica son fundamentales la longitud, la masa y el tiempo. Son también fundamentales la temperatura, la intensidad luminosa y la carga eléctrica. MAGNITUDES DERIVADAS: Surgen al combinar las magnitudes fundamentales. Ejemplo: la unidad de fuerza llamada Newton (N), que equivale a Kg . m/s² o la unidad de trabajo que es "Julio" que equivale a N . m. APARATOS DE MEDIDA: Para la longitud se utiliza el metro; el calibrador, el tornillo micrométrico y el esferómetro que sirve para medir el espesor de una lámina y e1 radio de una esfera. Para la masa se utiliza la balanza: para el tiempo se emplea el cronómetro y para la temperatura el termómetro. SISTEMAS DE UNIDADES: Magnitud Sistema Internacional Longitud Masa Tiempo Metro (m) Kilogramo (Kg) Segundo (s) Sistema Cegesimal Centímetro (cm) Gramo (g) Segundo (s) Sistema Inglés Pie (ft) Libra (lb) Segundo (s) CONVERSION DE UNIDADES Se presenta una tabla de conversión de unidades para la longitud, entonces, para poder hacer una conversión de unidades para longitudes aplicamos el procedimiento según el siguiente ejemplo: Ejemplo: Convertir 1,5 km a m. La unidad km (que es la que queremos simplificar) está en el numerador (no hay denominador en este caso) y por lo tanto en la fracción por la que multiplicamos la escribimos en el denominador. De esta manera se pueden simplificar. Ahora escribimos la unidad a la que queremos llegar en la otra parte de la fracción (el numerador en este caso). Escribimos un 1 en la unidad más grande (kilómetro es más grande que metro). Escribimos la cantidad equivalente en la otra unidad (1 km equivale a 1000 metros). Hacemos la multiplicación y obtenemos el resultado. TALLER DE UNIDADES 1. Marcela compró un TV de 51 pulgadas y lo desea ubicar en una mueble de la sala, ¿cuántos centímetros son?, ¿cuántos metros? y ¿cuántos pies? Y si ¿le alcanza a caber en un espacio de 90cm? 2. Según la etiqueta de un frasco de aderezo para ensalada, el volumen del contenido es 0.473 litros (L). Use sólo las conversiones 1L = 1,000 cm3 para expresar dicho volumen en cm cúbicos. 3. ¿Cuántos segundos hay en una semana, sabiendo que en un minuto hay 60 s, y en cada hora 60 minutos y un día tiene 24 horas y una semana tiene 7 días? 4. Si se tiene 3,5 arrobas de plátanos, ¿a cuántas libras equivale?, ¿a cuántos kilogramos? Debes saber que 1 arroba contiene 25 libras y 1 libra son 453 gramos o 0,453 kilogramos. 5. Si la estrella más cercana a nosotros es Alfa Centauri que está a 4,37 años-luz, ¿cuántos kilómetros son?, (Recuerda que 1 año luz corresponde a la distancia que recorre la luz en un año a razón de 300.000 km por cada segundo) 6. Cierto automóvil híbrido que consume poco combustible tiene un rendimiento de gasolina de 55.0 mpg (millas por galón). a) Si usted va manejando dicho auto en Europa y quiere comparar su rendimiento con el de otros automóviles europeos, exprese tal rendimiento en km/L (L = litro). b) ¿Si el depósito de gasolina de este automóvil tiene una capacidad de 45 L, ¿cuántas veces deberá llenar el depósito de gasolina para conducir 1.500 km? 7. Supongamos que un corredor sobre una pista rectilínea cubre una distancia de 1 Km en 4 min exactamente. ¿Cuál es su velocidad media: a) en Km/h; b)en pies/s; c)en cm/s? 8. A cuanto equivale: f) 65 libras a kg. a) 4500 m en km. b) 7 pies a m, c) 100 km/h a m/s. d) 5 millas a km. e) 7 kg a g. CINEMÁTICA Parte de la física encargada de estudiar el movimiento, como se mueven los cuerpos en la naturaleza. Hace más de 2,000 años, los antiguos científicos griegos estaban familiarizados con algunas de las ideas de la física que estudiamos en la actualidad. Todo se mueve, hasta lo que parecería estar en reposo. Todo se mueve en relación con el Sol y las estrellas. Mientras estás leyendo este libro, te mueves a unos 107,000 kilómetros por hora en relación con el Sol, y te mueves aún más rápido con respecto al centro de nuestra galaxia. Fue Galileo, el principal científico de principios del siglo XVII, quien dio crédito a la idea de Copérnico de una Tierra en movimiento. Aunque no fue el primero en señalar los problemas en las ideas de Aristóteles, Galileo demolió con facilidad la hipótesis de Aristóteles acerca de la caída de los cuerpos. Se dice que Galileo dejó caer objetos de varios pesos desde lo más alto de la Torre Inclinada de Pisa, y luego comparó las caídas. Al contrario de la aseveración de Aristóteles, Galileo encontró que una piedra con el doble de peso que otra no caía con el doble de rapidez. A excepción del pequeño efecto de la resistencia del aire, encontró que los objetos de distinto peso, cuando se sueltan al mismo tiempo, caían juntos y llegaban al suelo en el mismo momento. Se dice que en una ocasión Galileo reunió a un gran número de personas para que atestiguaran la caída de dos objetos de distinto peso que lanzaría desde lo alto de la torre. Dice la leyenda que muchos de quienes observaron se mofaron del joven Galileo y continuaron apegándose a las enseñanzas aristotélicas. Trayectoria: es la línea imaginaria que une a las sucesivas posiciones que ocupa un objeto respecto a un sistema de referencia. Espacio recorrido: es la distancia recorrida sobre la trayectoria entre la posición inicial y final. Desplazamiento: Es la diferencia entre la posición final sf y la posición inicial so. El valor del desplazamiento es la distancia medida en línea recta entre la posición final y la inicial. *Importante: desplazamiento y espacio recorrido solamente coinciden si la trayectoria seguida por el móvil es recta y no se realice ningún cambio de sentido. *Importante: el desplazamiento total será cero si la posición final e inicial coinciden, es decir, si se vuelve al mismo punto de partida. Fíjate además que el espacio recorrido no es nunca nulo, siempre que haya movimiento. EJEMPLO: En el siguiente gráfico, que ilustra la trayectoria, calcular: el recorrido y el desplazamiento. Solución: a). Recorrido total, se calcula sumando los diferentes recorridos parciales, es decir determinando los cambios de posición entre los intervalos de tiempo: X = 6m + 0m + 3m + 0m + 6m + 9m = 24m b). Desplazamiento, se calcula sumando los desplazamientos parciales, es decir determinando los avances como positivos y los retrocesos como negativos entre los intervalos de tiempo: → = 6m + 0m − 3m + 0m + 6m − 9m = 0 m X TALLER SOBRE GRAFICAS Responda a cada pregunta en el cuaderno y solucione cada ejercicio con el procedimiento completo: 1. En cada gráfica se describe el movimiento de un cuerpo, ¿cuánto vale el recorrido total? a. b. c. 2. Según las anteriores gráficas, ¿Cuál es el valor del desplazamiento total? 3. En las anteriores gráficas, ¿entre qué tiempos se puede observar que el cuerpo no se mueve? 4. Volviendo a las gráficas, ¿entre qué tiempos el cuerpo se mueve con mayor rapidez instantánea? Y ¿cuál es su valor? 5. Calcula la rapidez media en cada gráfica. 6. ¿Puede suceder que una abeja durante un tiempo determinado en su vuelo tenga un recorrido de 60 m y el desplazamiento sea cero? 7. Elabora una tabla y la gráfica en el plano cartesiano correspondiente de tal manera que los valores del recorrido total sea de 180 m y lo haga en un tiempo total de 30 s. Además, que el desplazamiento total sea de 90 m. Rapidez A Galileo Galilei se le da el crédito de ser primero en medir la rapidez al considerar la distancia que se cubre durante cierto tiempo. Definió la rapidez como la distancia recorrida por unidad de tiempo. Rapidez = Distancia Tiempo Un ciclista que recorre 30 metros en un tiempo de 2 segundos, por ejemplo, tiene una rapidez de 15 metros por segundo. Rapidez instantánea Las cosas que se mueven a menudo tienen variaciones en la rapidez. Un automóvil, por ejemplo, puede recorrer una calle a 50 km/h, detenerse hasta 0 km/h con la luz roja del semáforo, y acelerar sólo hasta 30 km/h debido al tránsito vehicular. Puedes saber en cada instante la rapidez del automóvil observando el velocímetro. La rapidez en cualquier instante es la rapidez instantánea. En general, cuando un automóvil viaja a 50 km/h, sostiene esa rapidez durante menos de una hora. Si lo hiciera durante toda una hora, recorrería los 50 km. Si durara media hora a esa velocidad, recorrería la mitad de esa distancia, es decir, 25 km. Si sólo durara 1 minuto, recorrería menos de 1 km. Rapidez media Cuando se planea hacer un viaje en automóvil, el conductor desea saber el tiempo de recorrido. Lo que considera es la rapidez promedio o rapidez media, en el viaje. La rapidez media se define como: Rapidez media = Distancia total recorrida Tiempo del recorrido Si tu rapidez media es 80 kilómetros por hora durante un viaje de 4 horas, por ejemplo, recorres una distancia total de 320 kilómetros. Velocidad Cuando se conocen tanto la rapidez como la dirección de un objeto, estamos especificando su velocidad. Cuando decimos que un automóvil viaja a 60 km/h, por ejemplo, nos referimos a su rapidez. Pero si señalamos que se mueve 60 km/h al norte especificamos su velocidad. A una cantidad cómo la velocidad, que especifica tanto dirección como magnitud se le denomina cantidad vectorial. La velocidad límite en el universo es de 300.000 km/s. 𝒗= ⃗ 𝒙 𝒕 ⃗ 𝑒𝑠 𝑑𝑒𝑠𝑝𝑙𝑎𝑧𝑎𝑚𝑒𝑛𝑡𝑜 𝑦 𝒕 𝑡𝑖𝑒𝑚𝑝𝑜 𝑑𝑜𝑛𝑑𝑒 𝒙 EJEMPLO: En el gráfico, que ilustra la trayectoria, calcular: la velocidad media y la rapidez media a). Velocidad Media, se calcula dividiendo el desplazamiento total entre el tiempo total: → 𝑉𝑒𝑙𝑜𝑐𝑖𝑑𝑎𝑑 𝑀𝑒𝑑𝑖𝑎: →= 𝑉 𝑋 𝑡 = 0𝑚 = 0 𝑚/𝑠 6𝑠 b). Rapidez Media, se calcula dividiendo el recorrido total entre el tiempo: 𝑅𝑎𝑝𝑖𝑑𝑒𝑧 𝑀𝑒𝑑𝑖𝑎: 𝑉= 𝑋 24 𝑚 = = 4 𝑚⁄𝑠 𝑡 6𝑠 Un bus que se mueve en una trayectoria circular puede tener una rapidez constante, pero no una velocidad constante, ya que la dirección del movimiento cambia a cada instante. TALLER SOBRE MU: 1. Si 45 km/h es la velocidad de un cuerpo, ¿a qúe es equivalente en m/s y en mll/h? 2. Según el gráfico, ¿cuál es la velocidad del cuerpo en movimiento?, 3. Según el mismo gráfico, ¿cuál es el desplazamiento del cuerpo durante 30 min? 4. Un auto con velocidad constante de 70 km/h, parte de una ciudad, si al cabo de 0,8 h, ¿qué distancia lo separa de la ciudad? 5. Si el auto del punto anterior, ha recorrido 180 km, ¿Cuánto tiempo ha pasado después de salir de la ciudad origen? 6. Un auto que viaja en línea recta 200 km, luego regresa 100 km y gasta un tiempo de 5 horas en todo el recorrido, ¿cuál es la velocidad promedio? 7. Si un automóvil se mueve con una rapidez media de 60 km/h durante una hora, recorre una distancia de 60 km. ¿Cuánto hubiera recorrido si se moviera con esa rapidez durante 4 h?. ¿Y durante 10 h? 8. ¿Cuál es la rapidez de impacto de un automóvil que se mueve a 100 km/h y que golpea por detrás a otro que va en la misma dirección a 98 km/h? 9. Un avión vuela hacia el norte a 700 km/h, mientras que otro vuela hacia el sur a 700 km/h. ¿Son iguales sus rapideces? ¿Son iguales sus velocidades? Aceleración Podemos cambiar la velocidad de algo al modificar su rapidez, su dirección o ambas. El qué tan rápido cambia la velocidad es lo que entendemos por aceleración: 𝐴𝑐𝑒𝑙𝑒𝑟𝑎𝑐𝑖𝑜𝑛 = 𝐶𝑎𝑚𝑏𝑖𝑜 𝑑𝑒 𝑣𝑒𝑙𝑜𝑐𝑖𝑑𝑎𝑑 𝐼𝑛𝑡𝑒𝑟𝑣𝑎𝑙𝑜 𝑑𝑒 𝑡𝑖𝑒𝑚𝑝𝑜 Decimos que un cuerpo tiene aceleración cuando hay un cambio en su estado de movimiento. Estamos familiarizados con la aceleración de un automóvil. 𝑎= ⃗⃗⃗⃗ ⃗⃗⃗⃗𝑜 𝑣𝑓 −𝑣 𝑡 El conductor siente una rápida desaceleración, al ser impulsado hacia adelante Cuando el conductor pisa el acelerador, los pasajeros experimentamos aceleración conforme nos recargarnos más contra los asientos. La idea clave que define la aceleración es el cambio. Supongamos que al manejar aumentamos, en un segundo, nuestra velocidad de 30 a 35 kilómetros por hora, y en el siguiente segundo a 40 kilómetros por hora, y a 45 en el siguiente y así sucesivamente. Cambiamos la velocidad en 5 kilómetros por hora cada segundo. Este cambio de velocidad es lo que entendemos por aceleración. TALLER SOBRE ACELERACIÓN: 1. Si en 5 segundos un auto que avanza en línea reta aumenta su rapidez de 50 km/h a 65 km/h, en tanto que un camión pasa del reposo a 15 km/h en línea recta. ¿Cuál de los dos vehículos experimenta una aceleración mayor?, ¿Cuál es el valor de las aceleraciones? 2. Calcule la velocidad de un patinador que acelera desde el reposo, durante 3 segundos, al descender por una rampa con una aceleración de 5 m/s2. 3. ¿Qué tiene mayor aceleración, un avión que pasa de 1,000 a 1,005 km/h en 10 segundos, o una patineta que pasa de 0 a 5 km/h en 1 segundo? 4. Calcula la aceleración de un autobús que va desde los 10 km/h hasta una rapidez de 50 km/h en 10 segundos. 5. Calcula la aceleración de una pelota que parte del reposo, desciende rodando por una rampa y gana una rapidez de 25 m/s en 5 segundos. 6. ¿Cuál es la aceleración de un automóvil que mantiene una velocidad constante de 100 km/h durante 10 s? 7. ¿Con qué velocidad debería venir un bus si necesitó 8,5 s para frenar y detenerse completamente con 4,3 m/s2? MOVIMIENTO UNIFORMEMENTE ACELERADO El movimiento rectilíneo uniformemente variado se caracteriza porque su trayectoria es una línea recta y la velocidad varía proporcionalmente al tiempo. Por consiguiente, la aceleración es constante, ya que la velocidad varía uniformemente con el tiempo. Este movimiento puede ser acelerado si la velocidad aumenta a medida que transcurre el tiempo y retardado si la velocidad disminuye en el transcurso del tiempo. 𝑎= 𝑉𝑓 − 𝑉𝑜 𝑡 𝑥 = 𝑉𝑜 . 𝑡 + 𝑎 ∶ 𝐴𝑐𝑒𝑙𝑒𝑟𝑎𝑐𝑖ó𝑛 𝑒𝑛 𝑚⁄ 2 𝑜 𝑘𝑚⁄ 2 𝑠 ℎ 𝑉𝑓2 = 𝑉𝑜2 + 2. 𝑎. 𝑥 𝑎. 𝑡 2 2 𝑉𝑓 ∶ 𝑉𝑒𝑙𝑜𝑐𝑖𝑑𝑎𝑑 𝐹𝑖𝑛𝑎𝑙 𝑥 ∶ 𝐷𝑖𝑠𝑡𝑎𝑛𝑐𝑖𝑎 𝑒𝑛 𝑚, 𝑘𝑚, 𝑐𝑚 𝑜 𝑚𝑖𝑙𝑙 𝑥 = 𝑡. (𝑉𝑓+ 𝑉𝑜 ) 2 𝑉𝑜 : 𝑉𝑒𝑙𝑜𝑐𝑖𝑑𝑎𝑑 𝑖𝑛𝑖𝑐𝑖𝑎𝑙. 𝑡: 𝑇𝑖𝑒𝑚𝑝𝑜 𝑒𝑛 𝑠, 𝑚𝑖𝑛, ℎ TALLER SOBRE MUA: 1. En una carrera de motocicletas, partiendo del reposo, un motociclista alcanza los 120 km/h en 8 segundos. ¿Cuál es la aceleración?, ¿Cuánta distancia alcanza a recorrer en ese tiempo? 2. Un ciclista que va a 30 km/h, aplica los frenos y logra detener la bicicleta en 4 segundos. Calcular: a) ¿Qué desaceleración produjeron los frenos?. b) ¿Qué espacio necesito para frenar? 3. Un avión, cuando toca pista, acciona todos los sistemas de frenado, que le generan una desaceleración de 20 m/s², necesita 100 metros para detenerse: a) ¿Con qué velocidad toca pista?. ¿Qué tiempo demoró en detener el avión? 4. En plena vía un conductor de bus que viaja a 85 km/h frena bruscamente quedando en reposo después de 3,5 segundos, ¿alcanza a atropellar a un gato que pasa a 30 metros del bus? 5. Un automóvil que viaja a una velocidad constante de 120 km/h, demora10 s en detenerse: a) ¿Qué espacio necesitó para detenerse?. b) ¿Con qué velocidad chocaría a otro vehículo ubicado a 30 m del lugar donde aplicó los frenos? Caída libre Qué tan rápido los objetos caen a causa de la fuerza de gravedad. Cuando un objeto que cae está libre de toda restricción —sin fricción de aire ni de cualquier otro tipo—, y cae bajo la sola influencia de la gravedad, ese objeto se encuentra en caída libre. La aceleración de la caída libre es aproximadamente de 10 metros por segundo cada segundo o, en notación compacta, es 10 m/s2. En el caso de los objetos en caída libre se acostumbra el uso de la letra g para representar la aceleración (ya que la aceleración se debe a la gravedad). El valor de g es muy distinto en la superficie lunar o en la superficie de los demás planetas. Aquí en la Tierra g su valor promedio es 9.8 metros por segundo cada segundo o, en notación compacta, 9.8 m/s2. Hasta aquí hemos considerado objetos que se mueven directo hacia abajo, en dirección de la gravedad. ¿Y si se avienta un objeto directo hacia arriba? Una vez lanzado continúa moviéndose hacia arriba durante algún tiempo, y después regresa. En su punto más alto, al cambiar su dirección de movimiento de hacia arriba a hacia abajo, su rapidez instantánea es cero. A continuación comienza a ir hacia abajo exactamente como si se hubiera dejado caer desde el reposo a esa altura, con la misma aceleración conque cae sube (g = 9,8 m/s2). Lo común es observar que muchos objetos caen con aceleraciones distintas. Una hoja de árbol, una pluma o una hoja de papel pueden llegar al suelo con lentitud. El hecho de que la resistencia del aire sea la causa de esas aceleraciones distintas se puede demostrar muy bien con un tubo de vidrio hermético que contenga objetos livianos y pesados, por ejemplo, una pluma y una moneda. En presencia del aire, ambas caen con aceleraciones muy distintas. No obstante, si se saca el aire del tubo, al invertirlo rápidamente se ve que la pluma y la moneda caen con la misma aceleración. Las ecuaciones de la velocidad y de la altura son las siguientes: v = gt h = 1/2 gt2 TALLER SOBRE CAIDA LIBRE: 1. Un gato baja de una cornisa y llega al suelo en 1/2 segundo. ¿Cuál es su rapidez al llegar al suelo? ¿Qué altura tiene la cornisa desde el piso? 2. ¿Qué velocidad adquiere un objeto en caída libre a los 5 s después de dejarse caer desde el reposo? ¿Y cuál es a los 6 s después? 3. ¿Cuál es la altura que cae un objeto, en caída libre, 1 s después de haber sido dejado caer desde el reposo? ¿Y espués de 4 s? 4. Una manzana cae de un árbol y golpea el suelo en 1.5 segundos. Calcula qué distancia recorrió en su caída. 5. Supón que las tres bolas parten al mismo tiempo de las partes superiores. ¿Cuál llega primero al suelo? Explica por qué. 6. Se lanza una bola directamente hacia arriba, con una rapidez inicial de 30 m/s. ¿Hasta qué altura llega y cuánto tiempo estará en el aire? 7. Si no hubiera resistencia del aire, ¿con qué rapidez caerían las gotas que se formaran en una nube a 1 km sobre la superficie terrestre? 8. Un fortachón lanza una piedra hacia arriba y alcanza una altura de 45 m, ¿Cuánto demora la piedra en el aire?, ¿Con qué velocidad fue lanzada?