AP - Cadena C. et al. (2018) - Comparación de tipos de flujos, para diferentes secciones de canales.

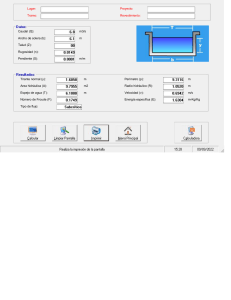
See discussions, stats, and author profiles for this publication at: https://www.researchgate.net/publication/322555700
Comparación de tipos de flujos, para diferentes secciones de canales.
Article · January 2018
CITATIONS
READS
0
3,042
3 authors, including:
Milton Roque Saltos Quiñónez
Escuela Superior Politécnica del Litoral (ESPOL)
1 PUBLICATION 0 CITATIONS
SEE PROFILE
Some of the authors of this publication are also working on these related projects:
Comparación de tipos de flujos, para diferentes secciones de canales. View project
All content following this page was uploaded by Milton Roque Saltos Quiñónez on 17 January 2018.
The user has requested enhancement of the downloaded file.
Escuela Superior Politécnica del Litoral
Comparación de tipos de flujos, para diferentes secciones de canales.
Comparación de tipos de flujos, para diferentes secciones de canales.
Cristhian Felix Cadena Cornejo, Milton Roque Saltos Quiñonez, Madelaine Del Carmen Villalta
Echeverría.
Facultad de Ingeniería en Ciencias de la Tierra
Escuela Superior Politécnica del Litoral (ESPOL)
Campus Gustavo Galindo, Km 30.5 vía Perimetral
Apartado 09-01-5863. Guayaquil-Ecuador
Email del autor(s) [email protected],[email protected], [email protected].
Resumen
La disposición geométrica que tenga un canal y los caudales para los que son diseñados, ocasionan que el flujo se
comporte de diferente manera, esto debe ser, considerado en el proceso de diseño, puesto que puede ocasionar desgaste
innecesario en el canal, ocasionando pérdidas económicas; un tipo de disposición geométrica, puede ser más viable en
términos constructivos que otra, mejor vista socialmente, por la comunidad afectada por la obra, el impacto ambiental
de la misma, o si es factible de elaborar. Los canales artificiales son los más utilizados, dentro de los que podemos
observar figuras geométricas conocidas, adaptadas al requerimiento del área de construcción y de la disponibilidad
económica.
En este artículo, se realiza el estudio de cinco geometrías, mediante el uso de un software de programación, estableciendo
casos particulares, para así poder determinar, que geometría sería recomendable utilizar en dichos casos, con lo que,
dio como resultado, mediante el análisis de que, debido al tirante crítico, tirante normal, velocidades, que se produjeron
en los diversos canales, se eligió como la más factible en términos de optimización de las propiedades del terreno y que
se adapta mejor a requerimientos técnicos constructivos, tomando en cuenta las velocidades recomendadas para que el
canal no se vea visto afectado por sedimentos o posibles socavaciones o desgaste innecesario de material, es la sección
semicúbica, ya que al analizar la misma con una pendiente ‘suave’, se encuentra en un régimen sub-crítico, donde si
bien es cierto que todas las secciones presentan similares valores de velocidad, esta es la sección que menor área ocupa.
Palabras Claves: Geometría de canales, flujo crítico, flujo sub-crítico, pendiente suave, coeficiente de Manning,
velocidad máxima permisible, perímetro mojado, tirante, flujo uniforme.
1. Introducción
Para el ser humano ha sido de vital importancia,
tener la capacidad de controlar los recursos
hídricos que estén a su alcance, con la finalidad de
poder distribuirlos equitativamente a toda una
población o región, tratarlos y almacenarlos de
manera eficiente, para realizar la actividad para la
que fueren requeridos. En el estudio de la
hidráulica de canales, existen diversas
disposiciones geométricas por la que un fluido
puede circular, ya sea desde geometrías
completamente irregulares y discontinuas como
ríos; o secciones regulares diseñadas por el
hombre.
Para esto, la geometría de un canal es de gran
importancia, puesto que, la disposición
geométrica que este tenga y los caudales para los
que son diseñados los canales, ocasionan que el
flujo se comporte de una manera u otra. Este
comportamiento, se debe considerar siempre en el
proceso de diseño, puesto que puede ocasionar
desgaste innecesario en el canal, ocasionando
pérdidas económicas; así mismo, un tipo de
disposición geométrica puede ser más viable en
términos constructivos que otra, aceptada
socialmente por la comunidad afectada debido a la
obra, el impacto ambiental de la misma, o la que
sea más factible de elaborar por el ingeniero.
Se analizará, que geometría puede ser óptima para
diversos tipos de obras hidráulicas, tales como: los
canales dispuestos por los egipcios, alrededor del
Nilo para proveerse de agua, debido a que esas
zonas son desérticas, aliviaderos en prensas
hidráulicas, canales de riego que dotan de líquido
vital a regiones donde es muy difícil acceder a
esta, sistemas de alcantarillado para una ciudad,
entre otros (Bello, 1914).
2. Revisión de literatura
2.1. Tipos de Canales
Existe más de una modalidad de clasificación para
canales. La más básica, se obtiene cuando, el
criterio que se emplea es, el procedimiento
utilizado para crearlos (Cadavid, 2006):
- Canales naturales
- Canales artificiales
2.1.1. Canales Naturales
Todos los cursos de agua que existen de manera
natural, desde pequeños arroyos, hasta grandes
1
Escuela Superior Politécnica del Litoral
Comparación de tipos de flujos, para diferentes secciones de canales.
ríos; su geometría puede ser muy irregular
(Campo & Aldalur & Férnandez, 2012).
2.1.2. Canales Artificiales
Son los canales, construidos mediante la mano del
hombre, tales como: canales de riego, de
navegación, control de inundaciones, canales de
centrales hidroeléctricas, alcantarillado pluvial,
sanitario, canales de desborde, canaletas de
madera, cunetas a lo largo de carreteras, cunetas
de drenaje agrícola y canales de modelos
construidos en el laboratorio (Ruiz, 2008).
Los canales artificiales, tienen por lo general,
secciones geométricas de forma y dimensiones
constantes en tramos más o menos largos (Soleto,
2002). Los canales curvos tienen propiedades
hidráulicamente más estables, puesto a que tienen
menos quiebres donde pueden aparecer grietas
producto de concentración de esfuerzos, además
de tener una mayor capacidad de flujo.
(Mironenko AP, 1984)
hidráulicas (Goulart & Anflor & Möller, 2013), se
caracteriza por la independencia de las
magnitudes del flujo con el tiempo, lo que, a su
vez, implica la constancia de las condiciones de
borde, en los canales donde se verifica el
movimiento de agua (Méndez, 2001).
2.2.2. Energía Específica.
Energía total del flujo de un canal abierto, cuando
el datum coincide con el lecho del canal, en una
sección dada (Subramanya K., 2009).
Esta energía no es una expresión realista de la
energía total de un fluido, puesto que, la carga de
elevación se la considera como cero. (Sengel &
Cimbala, 2006). Por lo tanto, se considera la
energía específica como el total de: la carga
hidráulica (y) más la carga dinámica (v^2/2g) de
un líquido que fluye en un canal abierto
(Bakhmeteff, 1932).
𝑬= 𝒚+
𝑽𝟐
𝟐𝒈
Ec. 1
De acuerdo con Cadavid, en su libro Hidráulica de
Canales
Fundamentos,
describe
las
configuraciones geométricas como sigue:
Ilustración 3: Definición de Energía Específica (Subramanya K., 2009).
Ilustración 1: Canal Prismático con sección transversal
Ilustración 2: Tipos de secciones transversales artificiales
2.1.3. Secciones cerradas
Sección circular: El círculo es la sección más
común para alcantarillados y alcantarillas de
tamaños pequeño y mediano. (Kay M, 2008)
Sección parabólica: Se usan comúnmente para
alcantarillas y estructuras hidráulicas importantes.
2.2. Flujo en Canales
2.2.1.
Régimen Permanente
En una sección de canal, permanecen constantes
con respecto al tiempo, las características
2.2.3. Número de Froude y Regímenes de
Flujo.
Se lo representa como la relación entre las fuerzas
inerciales y las fuerzas gravitacionales. (Fox &
McDonalds, 2011), y este expresa el régimen de
flujo en un canal, que es dado por (Jaromír &
Zbyněk,2015):
𝑭𝑹 =
𝑽
Ec. 2
√𝒈𝑳𝒄
Donde V: velocidad promedio en una sección
transversal, g: aceleración de la gravedad y Lc el
tirante o profundidad del flujo.
El número de Froude, define en qué tipo de
régimen se encuentra el flujo en canal abierto:
Fr<1:
Régimen
subcrítico:
Representa
velocidades bajas, las perturbaciones (ondas)
pueden ir aguas arriba. Para este régimen de flujo
2
Escuela Superior Politécnica del Litoral
Comparación de tipos de flujos, para diferentes secciones de canales.
las fuerzas inerciales son sobrepasadas en
importancia por las gravitacionales; se tienen
velocidades y pendientes bajas, pero las
profundidades de la lámina del agua, por el
contrario, son mayores que las que se presentan en
el flujo supercrítico. Para este tipo de flujo un
aumento en la energía se traduce en un aumento
en la profundidad de la lámina de agua. El número
de Froude en este estado es menor a 1. (Rivas,
2013).
Fr>1: Régimen supercrítico: Representa
velocidades altas, donde las ondas o
perturbaciones son arrasadas por la velocidad de
flujo aguas abajo (Kay M., 2008). En este tipo de
flujo las fuerzas inerciales presentan una
influencia mucho mayor que las fuerzas
gravitacionales, se presenta a velocidades y
pendientes altas y a profundidades más pequeñas.
Cuando existe un flujo de este tipo en un canal un
aumento en la cantidad de energía provoca una
disminución de la profundidad de la lámina de
agua. El número de Froude, en este caso, es mayor
a 1. Este estado de flujo propicia la formación de
resaltos hidráulicos; estos aumentan su capacidad
de disipación de energía en ciertos intervalos,
alcanzando la mayor capacidad para flujos con
Froude mayores a 9. (Barroso & Suta Ramirez,
2007)
Fr=1: Flujo crítico: transición entre flujo
subcrítico y flujo supercrítico, punto donde la
energía específica es mínima (Akan O., 2006), el
valor que toma depende únicamente de la
geometría del canal y de la velocidad de descarga.
(Subramanya K., 2009). Es un flujo inestable,
poco recomendable usarlo en el diseño de
estructuras hidráulicas. Se reconoce porque el
número de Froude es igual a 1, en este flujo no se
generan resaltos hidráulicos. (Barroso & Suta
Ramirez, 2007). Es un estado en que la energía
específica es mínima para un caudal determinado,
la corriente es inestable y está sujeta a
fluctuaciones de la profundidad del agua. (Rivas,
2013)
2.2.4 Tirante crítico.
Es la profundidad de flujo crítica, cuando en
número de Froude FR=1, para una descarga dada
en un ancho dado, y depende únicamente del
ancho del canal. (Dingman, 2009).
Flujo Uniforme.
En un canal abierto con un movimiento uniforme,
permanecen constantes las características
2.2.5
hidráulicas del flujo (Jaromír & Zbyněk, 2015), la
profundidad, el área, la velocidad media y el gasto
son constantes, la superficie libre y el fondo son
paralelas. (French, R. H., 1988)
El flujo uniforme se encuentra generalmente en
canales artificiales (Pizarro H., 1994), largos y
rectos con una sección transversal, rugosidad y
pendiente constante. (Sung M.K., 2015).
𝟐𝒈
𝑽 = √ 𝑪 √𝑹𝒉𝑺𝒃
Ec. 3
𝒇
Dónde: g: fuerza de la gravedad, Cf: factor de
fricción, Rh: Radio hidráulico y Sb: pendiente
normal y V: velocidad de flujo uniforme.
Ilustración 4: Flujo uniforme en un canal abierto. (Vatankhah A., 2012).
2.2.6 Coeficiente de Chezy.
Es un coeficiente de resistencia de flujo, debido a
que toma todos los parámetros relacionados a la
fricción (Cadavid J.H., 2006), que rige el flujo
permanente y uniforme, turbulento tanto para
tuberías y canales (Nasseri, 2017).
Ec. 4
2.2.7 Perímetro Mojado.
El perímetro mojado, se define como la suma de
la longitud de los perímetros de la sección que se
encuentra realmente en contacto con (esto es,
mojado por) el fluido. (Mott R., 2004).
A
B
Ilustración 5: Sección transversal de un canal. (Fuente propia).
𝟐
𝑩
𝒅𝒚
𝑷 = ∫𝑨 √𝟏 + (𝒅𝒙)
Ec. 5
2.2.8 Radio Hidráulico.
Dado que los canales abiertos vienen con
secciones transversales irregulares, el radio
hidráulico sirve como la longitud característica y
3
Escuela Superior Politécnica del Litoral
Comparación de tipos de flujos, para diferentes secciones de canales.
da uniformidad al tratamiento de canales abiertos
y permite estudiar el comportamiento del flujo
igual al de un tubo circular, siendo este la relación
entre el área mojada y el perímetro mojado.
(Mataix C., 2009)
𝑹𝒉 =
𝑨
Ec. 6
𝑷
2.2.9
2.2.1. Velocidad en Canales Abiertos
La velocidad en los canales, varían en un rango
cuyo límite son las velocidades mínimas que no
produzcan sedimentación y máxima que no
produzca erosión en las paredes y el fondo del
canal. En la tabla, se establecen los valores
mínimos permisibles de velocidades, debido al
tipo de material en el que está construido el canal.
(Rubio, 2013)
Ecuación de Manning.
Parte de la fórmula de Chézy para el cálculo de
velocidades del agua para tuberías y canales
(Goldfarb & da Silva & de Lima & de
Azevedo,2004).
Partiendo de la asunción:
𝒂
𝒏
𝟏/𝟔
𝑪 = 𝑹𝒉
Ec. 7
Dónde: n: coeficiente de Manning (depende de la
rugosidad del material); a: factor de conversión:
a=1m3/s (SI), sino a=1.49; Rh: radio hidráulico
(Sistema inglés) (Sengel & Cimbala, 2006).
Quedando de la siguiente manera:
𝒂
𝟐/𝟑
𝑽𝒐 = 𝒏 𝑹𝒉 𝑺𝟎.𝟓
𝒐
Ec. 8
2.2.10 Tirante normal.
Es el tirante el cual las fuerzas de flujo y las
fuerzas resistentes se equilibran (Gribbin, 2013).
Por lo que si la profundidad real está por encima o
por debajo del tirante norma ya no existiría
equilibrio de fuerzas. (Dingman, 2009)
Si la profundidad de flujo es mayor que la
profundidad normal, las fuerzas impulsoras
excederán las fuerzas resistentes, y el flujo tenderá
a acelerarse (E. Lorenzo, 2010). Por el contrario,
si la profundidad de flujo real es mayor a la
normal, la conducción de agua se ralentizará
puesto que las fuerzas resistentes serán mayores
que las de conducción. (Dingman, 2009).
2.2.11 Tirante.
Distancia “y” perpendicular a la plantilla, medida
desde el punto más bajo de la sección, hasta la
superficie libre del agua. (Sotelo, 2002).
2.2.12 Ancho de Superficie Libre.
Es el ancho “T” de la sección de canal, medido al
nivel de la superficie libre. (Sotelo, 2002).
Ilustración 6 Velocidades Permisibles.
2.3 Elementos geométricos
canales abiertos
de
los
Son propiedades de la sección transversal de un
canal, definidas por la geometría de la sección y la
profundidad del flujo. Las formas geométricas
más empleadas en el diseño de canales son las
rectangulares y trapezoidales; los ríos, a pesar de
tener una sección transversal irregular, pueden
aproximarse a una sección trapezoidal. (Orson W,
I., & Vaughn E, 2003).
Donde:
b: ancho del canal.
z: laderas laterales del canal.
y: tirante del canal
D: diámetro (en el caso de tuberías).
2.4
Secciones geométricas de canales.
Es la sección tomada en dirección del flujo, las
secciones naturales son muy irregulares por lo
general; las secciones artificiales son de formas
geométricas regulares, siendo las más utilizadas
(Lin & Wang & Tfwala & Chen, 2014):
2.4.1 Sección Trapezoidal.
Es la sección más recomendada cuando se hacen
excavaciones, puede estar recubierto de hormigón
armado, cuando la magnitud de la pendiente del
canal pueda inducir velocidades elevadas. (Kay
M, 2008)
Es evidente que, la inestabilidad del terreno
requiere de la utilización de taludes laterales
4
Escuela Superior Politécnica del Litoral
Comparación de tipos de flujos, para diferentes secciones de canales.
elevados, que podrían implicar una extensión
lateral excesiva por parte de la sección transversal
y una eventual invasión a los terrenos adyacentes
a la franja demarcada. (Ilustración 3).
modelando la forma de un canal triangular,
obteniendo lo siguiente:
Ilustración 7: Sección trapezoidal (fuente propia)
Ilustración 9: Sección de canal auxiliar con el valor zp correspondiente.
(Fuente propia)
El área de la sección trapezoidal se define como:
𝒅𝒇
𝒅𝒙
= 𝟐𝒌𝒙
Ec. 13
Donde b es el ancho de solera, z es la ladera
transversal del canal y y es el tirante.
Se puede observar que la pendiente del canal
auxiliar es 2k, entonces el valor de “zp” que es la
relación de la distancia horizontal y la distancia
vertical (fuente propia), sería:
El ancho de espejo se escribe como:
𝒛𝒑 = 𝟐𝒌
𝑨 = 𝒃𝒚 + 𝒛𝒚𝟐
Ec. 9
𝟏
𝑻 = 𝒃 + 𝟐𝒛𝒚
Ec. 10
Ec. 14
Quedando finalmente:
𝟏
𝒇(𝒙) = 𝟐𝒛 𝒙𝟐
El perímetro mojado:
Ec. 15
𝒑
𝑷 = 𝒃 + 𝟐𝒚√𝟏 + 𝒛𝟐
Ec. 11
La ecuación también se puede escribir de la
siguiente manera:
2.4.2 Sección Parabólica.
𝟒
Se emplea en algunas ocasiones, para canales
revestidos y es la forma que toman
aproximadamente muchos canales naturales y
canales viejos de tierra (Ruiz, 2008).
La ecuación de la sección parabólica está dada
por:
𝒇(𝒙) = 𝒌𝒙𝟐
Ec. 12
𝒇(𝒙) = 𝑩 𝒙𝟐 ; 𝑩 =
𝑻𝟐𝒎
Ec. 16
𝒉
Donde Tm es, el ancho de espejo de la sección del
canal y h es la altura total (tirante más borde libre).
(Achour & Khattaoui, 2008)
El área se puede expresar de la siguiente manera:
𝟑
𝟒
𝑨 = √𝒛𝒑 𝒉𝟐
𝟑
Ec. 17
El perímetro mojado:
𝑷𝒎 = 𝒛𝒑 [√
𝟐𝒚
(𝟏
𝒛𝒑
+
𝟐𝒚
𝟐𝒚
) + 𝐥𝐧 (√ +
𝒛𝒑
𝒛𝒑
𝟐𝒚
√𝟏 + 𝒛 )] Ec. 18
𝒑
Tirante crítico:
𝟒
𝟐𝟕𝑸𝟐
𝒚𝒄 = √𝟔𝟒𝒈𝒛
Ec. 19
𝒑
Tirante normal (Forma Explícita -> Aproximada):
Ilustración 8: Sección parabólica (fuente propia)
𝒚𝒏 =
Donde y es la ordenada de la sección transversal
del canal, k es un parámetro de forma, y x es la
abscisa. (Li Y, 2014)
Dado que resulta complicado entender el factor k,
se implementará un artificio, el cual hará que se
entienda mejor este factor, derivando la función f
en x, quedando finalmente una ecuación lineal,
𝜹𝒛𝒑
𝟐
𝟒/𝟏𝟓
[√𝒆𝜶 (𝟏 + 𝒆𝜶 ) + 𝐥𝐧(√𝒆𝜶 + √𝟏 + 𝒆𝜶 )]
Ec. 20
Donde:
𝟎.𝟒
𝜹=(
𝟏𝟖𝒏𝑸
)
Ec. 21
𝜶 = 𝟎. 𝟎𝟐[𝐥𝐧(𝜹)]𝟐 + 𝟏. 𝟐𝟐 𝐥𝐧(𝜹) + 𝟎. 𝟐𝟔
Ec. 22
𝟖/𝟑
𝟐.𝟖𝟖𝟒√𝑺𝒐 𝒛𝒑
5
Escuela Superior Politécnica del Litoral
Comparación de tipos de flujos, para diferentes secciones de canales.
2.4.3 Sección Semi-cúbica Parabólica sin solera
La forma del canal se define de la siguiente
manera:
𝟑
𝒇(𝒙) = 𝒂|𝒙|𝟐
Ec. 23
Donde a es el factor de forma del canal y se escribe
de la siguiente manera:
𝒂=
Ilustración 11: Sección Semi-Cúbica Parabólica con solera. (fuente propia).
𝟐𝒉√𝟐
Ec. 24
𝟑/𝟐
𝑻𝒎
Donde Tm es el ancho superior de la sección del
canal. Nótese que el factor a, se puede determinar
también, en función del tirante y del ancho de la
superficie del agua (Han, 2015).
El valor de a, es el similar al obtenido en la
ecuación (21)
El área se la obtiene de la siguiente manera (Han,
2015):
𝒚 𝟐/𝟑
𝒂
𝟔
𝟓
𝑨 = 𝒚( )
𝒚 𝟐/𝟑
𝑷=
[𝟑𝟔𝒂𝟐 (𝒂)
+ 𝒃𝒚
Ec. 30
𝟑/𝟐
+𝟏𝟔]
−𝟔𝟒
𝟏𝟎𝟖𝒂𝟐
+𝒃
Ec. 31
El ancho de corona de la sección del canal es:
𝑇𝑚 = 𝐵 + 𝑏
Ec. 32
Ilustración 10: Sección Semi-Cúbica Parabólica sin solera (fuente propia)
El área y perímetro mojado del canal se puede
escribir como:
𝟑
𝑨 = 𝟓 𝒚𝑻
𝑷=
𝑩𝟑
𝟖𝟒𝟔𝒚𝟐
Ec. 25
[(
𝟏𝟒𝟒𝒚𝟐
𝑻𝟐
𝟑
𝟐
+ 𝟏𝟔) − 𝟔𝟒]
Ec. 26
2.4.5 Sección Semi-Circular.
El área de se define como:
𝑨𝒎 =
𝑷𝒎 =
𝝑−𝒔𝒊𝒏(𝝑) 𝟐
𝑫
𝟖
𝑫𝝑
𝟐
; 𝒑𝒂𝒓𝒂 𝝑 ≤ 𝝅
Ec. 33
; 𝒑𝒂𝒓𝒂 𝝑 ≤ 𝝅
Ec. 34
Donde 𝜗 es el ángulo que se forma entre el centro
de la circunferencia y las esquinas del ancho de la
superficie de agua en el canal y D es el diámetro
de la sección. (Das, 2008)
Donde T se obtiene de la misma manera que Tm
en la ecuación (21). Quedando finalmente:
𝟐
𝑨=
𝑷=
𝟔
𝒚 𝟑
𝒚 ( 𝒂)
𝟓
𝟑/𝟐
𝒚 𝟐/𝟑
+𝟏𝟔] −𝟔𝟒
𝒂
𝟏𝟎𝟖𝒂𝟐
Ec. 27
[𝟑𝟔𝒂𝟐( )
Ec. 28
2.4.4 Sección Semi-Cúbica Parabólica con
solera.
La sección se define como:
𝒂|𝒙 + 𝒃/𝟐|
𝒙 ≤ −𝒃/𝟐
𝟎
−𝒃/𝟐 < 𝒙 < 𝒃/𝟐
𝒇(𝒙) = {
𝒂(𝒙 − 𝒃/𝟐)
𝒙 ≥ 𝒃/𝟐
Ec. 29
Ilustración 12: Sección semi-circula (fuente propia)
El tirante crítico:
𝒚𝒄 = [𝟎. 𝟕𝟕 (
3
𝒈𝟑 𝑫𝟏𝟓
𝑸𝟔
−𝟎.𝟎𝟖𝟓
) + 𝟏]
Ec. 35
Metodología.
En este artículo se comparará el comportamiento
de los parámetros más importantes empleados al
6
Escuela Superior Politécnica del Litoral
Comparación de tipos de flujos, para diferentes secciones de canales.
momento de analizar el flujo de agua en una
sección determinada de un canal abierto.
El modo que se realizarán las comparaciones será
calculando el tirante crítico, tirante normal,
velocidad, área mojada y perímetro mojado para
un determinado flujo de agua y pendiente en una
sección de canal.
2.3. Obtención
solicitados.
de
los
parámetros
Para obtener los parámetros se debe primero
conocer qué secciones de canales se usarán para
analizarlos y compararlos.
Las secciones de canales son:
• Semi-Cúbico Parabólica sin solera.
• Semi-Cúbico Parabólica con solera.
• Parabólico.
• Semi-Circular.
• Trapezoidal.
Luego se solicitan los datos de entrada, los cuales
son caudal, tipo de material, área y ancho máximo.
Seguidamente, definir las geometrías de los
canales: área, perímetro mojado, radio hidráulico,
y en caso de existir, ancho de solera, diámetro y
pendiente de talud.
Deducir las ecuaciones de tirante crítico y tirante
normal, aplicando la ecuación de Bernoulli y
Manning respectivamente, para el cual se
obtendrá en la mayoría de los casos a estudiar una
ecuación de forma implícita, por lo que se tendrá
que usar métodos numéricos, y así obtener los
parámetros solicitados.
Para obtener las ecuaciones pertenecientes a los
tirantes críticos y normales, debido a que resulta
complicado deducir y derivar dichas ecuaciones y
obtener la solución, se utilizará el lenguaje de
programación denominado Python, el cual, para
obtener la derivada de la energía específica en
función del tirante, se usará el método de las
diferencias finitas; y se calculará la solución con
el método de Newton-Raphson.
Mostrar tirante crítico, tirante normal, área
mojada, perímetro mojado, velocidad y en qué
régimen de flujo se encuentra.
de barras de tirantes vs secciones, velocidades vs
secciones, área vs secciones, y pendientes vs
secciones.
4
Resultados y discusión
4.1 Problemas:
A) Se desea construir un canal de drenaje con una
longitud de 10Km y con una sección transversal
máxima de 20m2, el cual va a transportar un
caudal de 15 m3/s. Dicho canal va a ser revestido
con Hormigón terminado con llana metálica (n=
0,013). Como condición para su construcción se
tienen que su ancho superficial no sea mayor a
10m. Además, se desea que se analicé para dos
distintos tipos de pendiente, una muy fuerte, y otra
suave de 1,5 por diez mil y de 0,002
respectivamente.
Con estos datos pruebe cual geometría de canal
entre las 6 analizadas presenta las mejores
condiciones para su construcción.
B) Con las secciones obtenidas en el problema
anterior, determine qué caudal cada sección de
canal va a rebosar, además calcular los tirantes
críticos y normales, las áreas y perímetros
mojados, y la velocidad de flujo para cada caudal.
4.2 Desarrollo:
Se utilizó el programa Python para cada geometría
de canal, y se calculó el tirante crítico aplicando el
método exacto, el tirante normal aplicando el
método iterativo de Newton – Raphson, a más de
las velocidades y perímetro mojado.
Puesto que los valores que definen a la geometría
del canal se los obtienen en base a las restricciones
propuestas, se tuvieron que deducir las siguientes
ecuaciones:
Sección trapezoidal:
De las ecuaciones Ec.9 y Ec.10 los valores de
ancho de solera y pendiente transversal del canal
son:
𝒃=
𝒛=
𝟐𝑨−𝑻𝒎 𝒉
𝒉
𝑻𝒎 𝒉−𝑨
𝒉𝟐
Ec. 36
Ec. 37
Finalmente tabular los resultados y comparar los
valores de los parámetros solicitados, diagramas
7
Escuela Superior Politécnica del Litoral
Comparación de tipos de flujos, para diferentes secciones de canales.
Donde b y z dependen del valor de h, dicho valor
que va a ser ingresado.
Sección semi-cúbica parabólica con solera.
Los parámetros a que se necesitan son en ancho de
solera b y el factor de forma a, el cual, partiendo
de la ecuación () y () se obtiene lo siguiente:
𝑨
𝒉
𝒃 = 𝟐. 𝟓 ∗ ( − 𝟎. 𝟔𝑻𝒎 )
Ec. 42
Y finalmente a partir de la Ec. 42:
𝒂 = (𝑻
𝟐𝒉√𝟐
𝒎 −𝒃)
Ec. 43
𝟑/𝟐
Obteniendo como resultado un caso similar al
canal trapezoidal, con los parámetros en función
de la altura.
Ilustración 13: Gráfica de b y z en función de h.
Resultados:
ℎ = 4.50𝑚
𝑏 = 1.10𝑚
𝑧=1
Sección parabólica:
Partiendo de la ecuación Ec. 16 e igualando a Ec.
14, la altura del canal h es:
𝑻𝟐
𝒉 = 𝟖𝒛𝒎
Ec. 38
𝒑
De la ecuación Ec.16 reemplazando a la ecuación
Ec. 36, el factor de forma zp se obtiene:
𝒛𝒑 =
𝑻𝒎
Ilustración 14: Gráfica de b y z en función de h.
Resultados:
ℎ = 3.80𝑚
𝑎 = 0.43𝑚
𝑏 = 1.40𝑚
Ec. 39
𝟔𝑨
Resultados:
𝑧𝑝 = 3.33𝑚 −1
ℎ = 3.80𝑚
Sección semi-cúbica parabólica sin solera.
Los parámetros a encontrar son el factor de forma
y la altura del canal, que se obtienen de las
ecuaciones Ec.24 y Ec.25:
Sección semicircular:
Para la sección circular, el único parámetro
geométrico a determinar es el diámetro del canal.
El cual se lo calcula con la ecuación del área de
una circunferencia.
𝟒𝑨
𝑫 = √𝟐𝝅
𝟓
𝑨
𝒉 = 𝟑 (𝑻 )
Ec. 40
𝒎
𝒂=
Ec. 44
Resultado:
𝐷 = 8𝑚
𝟐𝒉√𝟐
Ec. 41
𝟑/𝟐
𝑻𝒎
Resultados:
ℎ = 4.20𝑚
𝑎 = 0.38𝑚−0.5
8
Escuela Superior Politécnica del Litoral
Comparación de tipos de flujos, para diferentes secciones de canales.
IMPORTANTE:
Para las secciones parabólica y semicircular, el
tirante crítico se obtendrá de manera directa; y
solamente para la sección parabólica el tirante
normal se calculará mediante una ecuación
explícita.
Y para las demás secciones tanto el tirante normal
y crítico, se las determinará mediante el método
iterativo de Newton-Raphson.
Tirantes críticos
2.500
2.000
2.217
1.845
1.682
1.500
1.306
1.283
1.000
0.500
0.000
TRAPEZOIDAD PARABOLICO
Finalmente, luego de deducir las ecuaciones que
definen las propiedades de las secciones se
procede a obtener los resultados solicitados.
SEMICUBICO
SEMICUBICO SEMICIRCULAR
CON SOLERA
Gráfico 1: Comparación de tirantes críticos.
Tirantes normales
Pendiente 0,00015
Sección Trapezoidal:
𝑦𝑐 = 1,682 𝑚
𝑦𝑛 = 3,122 𝑚
𝑣 = 1,138 𝑚/𝑠
𝑃𝑚 = 9,931 𝑚
𝐴 = 13,182 𝑚2
Flujo Sub-Crítico
3.500
3.122
2.843
3.000
Flujo Sub-Crítico
2.000
1.500
1.000
0.500
0.000
TRAPEZOIDAD PARABOLICO
𝑦𝑐 = 2,217 𝑚
𝑦𝑛 = 2,843 𝑚
𝑣 = 1,149 𝑚/𝑠
𝑃𝑚 = 9,679 𝑚
𝐴 = 13,047 𝑚2
𝑦𝑐 = 1,845 𝑚
𝑦𝑛 = 2,584 𝑚
𝑣 = 1,167 𝑚/𝑠
𝑃𝑚 = 9,325 𝑚
𝐴 = 14,489 𝑚2
Flujo Sub-Crítico
SEMICUBICO SEMICIRCULAR
CON SOLERA
Área
15.000
14.489
14.500
14.000
13.182
13.054
13.048
12.855
13.000
12.500
12.000
TRAPEZOIDAD PARABOLICO
SEMICUBICO
SEMICUBICO SEMICIRCULAR
CON SOLERA
Gráfico 3: Comparación de áreas.
Flujo Sub-Crítico
Sección Semi Cúbica, con ancho de solera:
SEMICUBICO
Gráfico 2: Comparación de tirantes normales.
13.500
Sección Semi Cúbica:
2.423
2.500
Sección Parabólica:
𝑦𝑐 = 1,305 𝑚
𝑦𝑛 = 2,432 𝑚
𝑣 = 1,149 𝑚/𝑠
𝑃𝑚 = 9,715 𝑚
𝐴 = 13,053 𝑚2
2.584
2.432
Velocidades
1.200
1.150
1.167
1.138
1.149
1.150
1.100
1.035
1.050
1.000
0.950
Sección Circular:
𝑦𝑐 = 1,283 𝑚
𝑦𝑛 = 2,423 𝑚
𝑣 = 1,062 𝑚/𝑠
𝑃𝑚 = 9,693 𝑚
𝐴 = 12,855 𝑚2
TRAPEZOIDAD PARABOLICO
SEMICUBICO
SEMICUBICO SEMICIRCULAR
CON SOLERA
Gráfico 4: Comparación de velocidades.
Flujo Sub-Crítico
9
Escuela Superior Politécnica del Litoral
Comparación de tipos de flujos, para diferentes secciones de canales.
Pendiente 0,002
Sección Trapezoidal:
Perímetros mojados
10.400
10.148
10.200
10.000
9.800
𝑦𝑐 = 1,308 𝑚
𝑦𝑛 = 1,345 𝑚
𝑣 = 3,020 𝑚/𝑠
𝑃𝑚 = 6,120 𝑚
𝐴 = 4,99 𝑚2
9.931
9.716
9.680
9.600
9.325
9.400
9.200
9.000
Flujo Sub-Crítico
8.800
TRAPEZOIDAD PARABOLICO
SEMICUBICO
SEMICUBICO SEMICIRCULAR
CON SOLERA
Gráfico 5: Comparación de perímetros mojados.
Observando la velocidad alcanzada en cada uno
de los canales se puede decir que, la geometría
óptima sería la semi circular, dado que, además de
ser la sección que desarrolla una velocidad dentro
de lo permisible para un canal abierto, siendo
también mayor de todas, es la sección que menos
área consume. Teniendo como resultado un mayor
borde libre previendo posibles inundaciones.
La geometría no recomendable es la semi-cúbica
parabólica con ancho de solera, ya que, alcanza
una velocidad muy baja y esto provoca que el agua
no se distribuya correctamente de un punto a otro,
provocando posiblemente estancamiento, y poco
borde libre. Dando paso a inundaciones en los
alrededores de la obra, o también ocasionando
sedimentaciones y cambios en el área que
afectarían la geometría inicial del canal.
Al visualizar las gráficas de tirante normal y de
tirante crítico, se puede analizar que los valores
del tirante normal son mayores que los del tirante
crítico para todas las secciones estudiadas, lo que
indica que para esta pendiente se tiene flujo subcrítico en todas las secciones analizadas.
Sección Parabólica:
𝑦𝑐 = 1,305 𝑚
𝑦𝑛 = 1,305 𝑚
𝑣 = 2,922 𝑚/𝑠
𝑃𝑚 = 6,596 𝑚
𝐴 = 5,13 𝑚2
Flujo Crítico
Sección Semi Cúbica:
𝑦𝑐 = 2,217 𝑚
𝑦𝑛 = 1,603 𝑚
𝑣 = 2,986 𝑚/𝑠
𝑃𝑚 = 6,207 𝑚
𝐴 = 2,022 𝑚2
Flujo Súper-Crítico
Sección Semi Cúbica, con ancho de solera:
𝑦𝑐 = 1,845 𝑚
𝑦𝑛 = 1,340 𝑚
𝑣 = 2,650 𝑚/𝑠
𝑃𝑚 = 6,754𝑚
𝐴 = 5,660 𝑚2
Flujo Súper-Crítico
Sección Semi circular:
𝑦𝑐 = 1,283 𝑚
𝑦𝑛 = 1,270 𝑚
𝑣 = 2,922 𝑚/𝑠
𝑃𝑚 = 6,557 𝑚
𝐴 = 5,133 𝑚2
Flujo Súper-Crítico
Las velocidades obtenidas en las secciones usando
la pendiente de 1.5x10-4, se ve que son muy bajas
y no recomendables para un diseño de estas
magnitudes ya que todas son menores de 1.5m/s,
se correría el riesgo de que se produzca
estanqueidad y por ello se produzca
sedimentación y aparecimiento de vegetación en
el canal a construir; motivo por el cual se
seleccionó la sección semicircular.
Tirante crítico
2.500
2.217
1.845
2.000
1.500
1.308
1.306
1.283
1.000
0.500
0.000
Respecto al perímetro mojado se observa que la
sección semi-cúbica con ancho de fondo tiene el
mayor valor, siendo este un parámetro muy
importante en las fuerzas que resisten al flujo,
justificando la baja velocidad que se produce al
circular agua por este canal.
TRAPEZOIDAD PARABOLICO
SEMICUBICO
SEMICUBICO SEMICIRCULAR
CON SOLERA
Gráfico 6: Comparación de Tirantes Críticos
10
Escuela Superior Politécnica del Litoral
Comparación de tipos de flujos, para diferentes secciones de canales.
Tirante normal
2.000
1.603
1.500
1.346
1.341
1.306
1.270
1.000
0.500
0.000
TRAPEZOIDAD PARABOLICO
SEMICUBICO
SEMICUBICO SEMICIRCULAR
CON SOLERA
Gráfico 7: Comparación de Tirantes Normales.
Área
5.800
5.660
5.600
5.400
5.200
5.133
5.133
5.022
4.994
5.000
4.800
4.600
TRAPEZOIDAD PARABOLICO
SEMICUBICO
SEMICUBICO SEMICIRCULAR
CON SOLERA
Gráfico 8: Comparación de Áreas
Velocidad
3.100
3.020
3.000
2.987
2.922
2.922
2.900
2.800
sección semi-cúbica parabólica con ancho de
solera. Generando esta la menor velocidad de
flujo, puesto que, las velocidades de las demás
secciones están muy cercanas o superan los 3m/s.
Sin embargo en el caso de que se presente una
crecida en la descarga de agua, esta se puede
desbordar facilmente, por lo que esta condición de
debe tomar mucho en cuenta.
Las velocidades alcanzadas con esta pendiente son
mayores en todas las secciones en comparacion
con los valores obtenidos para las secciones con
pendiente de 1.5V:10000H, ocasionando que en la
sección trapezoidal se presente la mayor velocidad
que no es recomendable utilizar para el diseño que
se prevee realizar. Presupuesto considerable en el
mantenimiento del canal, es recomendandose
utilizar cualquiera de las otras secciones ya que
tienen valores permisibles de velocidades para
canales abiertos, y no se correria el riesgo de un
desgaste de material debido a la velocidad de
diseño. Ya que se establece según estudios
realizados que la velocidad maxima permisible
para un canal revestido con concreto es de 3m/s,
además de que quedaría un borde libre mucho más
alto.
2.650
2.700
2.600
Problema B:
Pendiente: 𝑆𝑜 = 1.5×10−4
2.500
2.400
TRAPEZOIDAD PARABOLICO
SEMICUBICO
SEMICUBICO SEMICIRCULAR
CON SOLERA
Gráfico 9: Comparación de Velocidades
Tirante crítico:
Semicúbico
Semicircular
con solera
15
1.682
1.306
2.217
1.904
1.283
20
1.935
1.508
2.751
2.416
1.486
25
2.154
1.686
3.252
2.902
1.665
30
2.349
1.846
3.728
3.366
1.827
35
2.526
1.994
4.185
3.814
1.977
40
2.688
2.132
4.626
4.247
2.116
Tabla 1: Valores de tirantes para cada sección de canal por cada caudal.
Q [m3/s] Trapezoidal Parabólico
Perímetro mojado
7.000
6.754
6.596
6.557
6.600
Semicúbico
6.208
6.200
6.121
5.800
TRAPEZOIDAD PARABOLICO
SEMICUBICO
SEMICUBICO SEMICIRCULAR
CON SOLERA
Gráfico 10: Comparación de Perímetro Mojado
Para este caso, se puede observar que al contrario
de lo que ocurria en los canales con la pendiente
de fondo de 1.5x10-4, el tirante critico va a ser
mayor que el tirante normal en todas las secciones.
Por lo que implicaría que el flujo en todas las
secciones geométricas son super-críticas.
Gráfico 11: Variación de tirante crítico en función del caudal.
Respecto a la sección óptima, obedeciendo las
velocidades permisibles en un canal revestido con
hormigón establecido en la Ilustración 6, sería la
11
Escuela Superior Politécnica del Litoral
Comparación de tipos de flujos, para diferentes secciones de canales.
Tirante normal:
Semicúbico
Semicircular
con solera
15
3.122
2.432
2.843
2.478
2.423
20
3.534
2.797
3.230
2.855
2.818
25
3.886
3.119
3.568
3.185
3.177
30
4.197
3.410
3.870
3.482
3.514
35
4.478
3.678
4.146
3.753
3.837
40
4.734
3.928
4.401
4.005
4.151
Tabla 2: Valores de tirantes para cada sección de canal por cada caudal.
Q [m3/s] Trapezoidal Parabólico
Semicúbico
Gráfico 14: Variación de la velocidad en función del caudal.
Perímetro mojado:
Semicúbico
Semicircular
con solera
15
9.931
9.716
9.680
9.648
9.325
20
11.096
10.650
10.712
10.634
10.166
25
12.092
11.454
11.595
11.483
10.909
30
12.971
12.169
12.377
12.237
11.592
35
13.764
12.819
13.083
12.920
12.240
40
14.490
13.418
13.730
13.548
12.868
Tabla 5: Valores de perímetros mojados de cada sección de canal por
caudal.
Q [m3/s]
Gráfico 12: Variación de tirante normal en función del caudal.
Trapezoidal Parabólico
Semicúbico
Área mojada:
Semicúbico
Semicircular
con solera
15
13.182
13.054
13.048
13.031
12.855
20
16.376
16.099
16.147
16.100
15.813
25
19.378
18.953
19.055
18.981
18.596
30
22.233
21.667
21.820
21.721
21.256
35
24.974
24.270
24.472
24.349
23.828
40
27.619
26.783
27.030
26.886
26.338
Tabla 3: Valores de áreas para cada sección por cada caudal.
Q [m3/s]
Trapezoidal Parabólico
Semicúbico
Gráfico 15: Variación del perímetro mojado en función del caudal.
Pendiente: 𝑆𝑜 = 2.0×10−3
Tirante crítico:
Q [m3/s] Trapezoidal Parabólico Semicúbico
Gráfico 13: Variación área en función del caudal.
Velocidad:
Semicúbico
Semicircular
con solera
15
1.138
1.149
1.150
1.151
1.167
20
1.221
1.242
1.239
1.242
1.265
25
1.290
1.319
1.312
1.317
1.344
30
1.349
1.385
1.375
1.381
1.411
35
1.401
1.442
1.430
1.437
1.469
40
1.448
1.493
1.480
1.488
1.519
Tabla 4: Valores de velocidades para cada sección por caudal.
Q [m3/s]
Trapezoidal Parabólico
Semicúbico
15
25
35
45
55
65
75
85
95
105
115
125
135
140
1.682
2.154
2.526
2.839
3.114
3.361
3.586
3.794
3.988
4.170
4.342
4.505
4.661
4.736
1.306
1.686
1.994
2.261
2.500
2.718
2.919
3.108
3.286
3.454
3.615
3.769
3.917
3.989
2.217
3.252
4.185
5.054
5.874
6.658
7.413
8.142
8.851
9.541
10.214
10.873
11.520
11.838
Semicúbico
Semicircular
con solera
1.904
1.283
2.902
1.665
3.814
1.977
4.669
2.247
5.482
2.489
6.261
2.710
7.013
2.915
7.742
3.108
8.452
3.289
9.144
3.461
9.820
3.626
10.483
3.783
11.133
3.934
11.454
4.008
Tabla 6: Valores de tirantes para cada sección de canal por caudal.
12
Escuela Superior Politécnica del Litoral
Comparación de tipos de flujos, para diferentes secciones de canales.
Gráfico 16: Variación del tirante en función del caudal.
Tirante normal:
Q [m3/s]
15
25
35
45
55
65
75
85
95
105
115
125
135
140
Trapezoidal Parabólico
1.745
2.207
2.565
2.866
3.128
3.362
3.574
3.770
3.952
4.123
4.284
4.436
4.581
4.651
1.306
1.667
1.959
2.212
2.437
2.643
2.834
3.012
3.180
3.340
3.492
3.638
3.778
3.847
Semicúbico
1.603
2.008
2.331
2.605
2.848
3.067
3.269
3.456
3.632
3.798
3.955
4.105
4.248
4.318
Semicúbico
Semicircular
con solera
1.300
1.270
1.680
1.631
1.986
1.929
2.249
2.191
2.484
2.429
2.696
2.649
2.893
2.858
3.076
3.056
3.248
3.247
3.410
3.432
3.565
3.612
3.713
3.788
3.855
3.961
3.924
4.047
Tabla 7: Valores de tirantes para cada sección de canal por caudal.
Gráfico 17: Variación del tirante en función del caudal
15
25
35
45
55
65
75
85
95
105
115
125
135
140
Trapezoidal Parabólico
4.966
7.297
9.404
11.366
13.223
14.999
16.708
18.362
19.969
21.534
23.063
24.560
26.027
26.750
Velocidad:
Semicúbico
Semicircular
con solera
15
3.020
2.922
2.987
2.953
2.922
25
3.426
3.377
3.419
3.401
3.398
35
3.722
3.709
3.735
3.727
3.748
45
3.959
3.976
3.988
3.988
4.029
55
4.159
4.201
4.202
4.208
4.266
65
4.334
4.396
4.388
4.399
4.471
75
4.489
4.569
4.554
4.568
4.652
85
4.629
4.725
4.703
4.720
4.815
95
4.757
4.868
4.840
4.860
4.962
105
4.876
4.999
4.966
4.988
5.096
115
4.986
5.121
5.083
5.107
5.220
125
5.090
5.235
5.193
5.219
5.333
135
5.187
5.342
5.296
5.323
5.438
140
5.234
5.393
5.345
5.374
5.488
Tabla 9: Valores de velocidad para cada sección de canal por caudal.
Q [m3/s]
Trapezoidal Parabólico
Semicúbico
Gráfico 19: Variación de la velocidad en función del caudal.
Perímetro mojado:
Área mojada:
Q [m3/s]
Gráfico 18: Variación del área en función del caudal.
5.133
7.403
9.436
11.318
13.093
14.787
16.415
17.988
19.516
21.003
22.456
23.877
25.271
25.958
Semicúbico
Semicúbico
Semicircular
con solera
5.022
5.080
5.133
7.312
7.351
7.358
9.371
9.390
9.339
11.282
11.283
11.169
13.088
13.070
12.893
14.812
14.777
14.538
16.469
16.419
16.120
18.072
18.007
17.653
19.628
19.548
19.145
21.143
21.050
20.603
22.623
22.517
22.033
24.071
23.952
23.438
25.491
25.359
24.824
26.190
26.053
25.510
Tabla 8: Áreas para cada sección de canal por caudal.
Semicúbico
Semicircular
con solera
15
6.037
6.596
6.208
6.389
6.557
25
7.341
7.649
7.380
7.477
7.496
35
8.356
8.460
8.284
8.325
8.213
45
9.206
9.137
9.037
9.038
8.812
55
9.947
9.728
9.694
9.661
9.337
65
10.608
10.258
10.280
10.221
9.811
75
11.210
10.742
10.813
10.731
10.250
85
11.764
11.189
11.304
11.203
10.661
95
12.279
11.606
11.761
11.643
11.052
105
12.762
11.998
12.190
12.056
11.426
115
13.216
12.369
12.595
12.447
11.789
125
13.647
12.723
12.979
12.819
12.142
135
14.058
13.060
13.345
13.174
12.489
140
14.256
13.224
13.521
13.345
12.661
Tabla 10: Perímetros mojados para cada sección de canal por caudal
Q [m3/s]
Trapezoidal Parabólico
Semicúbico
13
Escuela Superior Politécnica del Litoral
Comparación de tipos de flujos, para diferentes secciones de canales.
𝑑𝑦𝑐2
𝑑𝑄
𝑑𝑦𝑐
=
𝑑𝑄 𝑇𝑟𝑎𝑝𝑒𝑧𝑜𝑖𝑑𝑎𝑙
≅
𝑑𝑦𝑐
𝑑𝑄 𝑃𝑎𝑟𝑎𝑏ó𝑙𝑖𝑐𝑜
≅
𝑑𝑦𝑐
𝑑𝑄 𝑆𝑒𝑚𝑖−𝑐𝑖𝑟𝑐𝑢𝑙𝑎𝑟
Ec. 46
𝑑𝑦𝑐1
𝑑𝑄
Gráfico 20: Variación del perímetro mojado en función del caudal.
De las gráficas obtenidas al ir aumentando
gradualmente el caudal cada 5m3/s se observó que
tanto para pendiente fuerte como pendiente suave
los gráficos de los parámetros solicitados (yc, yn,
Am, v, Pm) en función del caudal, no tienen
diferencia alguna en el contexto de forma de las
curvas, tendencias de cada sección o canal que se
desborde primero. Sin embargo, se puede
constatar que en los resultados con la pendiente
fuerte, los crecimientos de tirantes normal y
crítico, área y perímetro mojado(a), y velocidad
son mucho mayores que los observados en las
gráficas con pendiente suave.
Teniendo como resultado los siguientes análisis:
Tirante crítico:
A medida que el caudal aumenta, la familia de
secciones semi-cúbicas tienen una tendencia
mucho más creciente que las secciones:
trapezoidal, parabólica y semi-circular.
La razón de crecimiento del tirante crítico
respecto al caudal, para las familias de canales
semi-cúbicos es aproximadamente lineal,
mientras que las demás secciones la tasa de
crecimiento disminuye a medida que el caudal
aumenta. Se puede observar también, que los
valores de tirantes para la sección parabólica y la
semi-circular son aproximadamente iguales.
Cabe recalcar que las variaciones del tirante
respecto a la variación del caudal de la familia con
mayor razón de cambio son aproximadamente
iguales; así mismo como las que tienen lento
crecimiento:
𝒅𝒚𝒄𝟏
𝒅𝑸
≅
𝒅𝒚𝒄
𝒅𝑸 𝑺𝒆𝒎𝒊𝒄𝒖𝒃𝒊𝒄𝒐
≅
𝒅𝒚𝒄
Ec.
𝒅𝑸 𝑺𝒆𝒎𝒊𝒄𝒖𝒃𝒊𝒄𝒐 𝒄𝒐𝒏 𝒔𝒐𝒍𝒆𝒓𝒂
>
𝑑𝑦𝑐2
𝑑𝑄
Ec. 47
Tirante normal:
La variación de tirantes respecto al caudal no
difiere tanto para cada sección de canal. Sin
embargo, con las secciones semi circular, semi
cúbica con fondo y parabólica a los 15m3/s el
tirante para la sección semi cúbica con solera esta
entre las dos mencionadas anteriormente, y a
medida que la descarga aumenta, a los 20m3/s este
los va a sobrepasar hasta los 95m3/s, donde se
vuelve a ubicar entre la parabólica y semi circular.
Área mojada:
Respecto al área el canal trapezoidal será el
primero en fallar. Se observó también que con el
caudal inicial la distancia entre áreas de cada
sección era muy baja, y cuando la descarga de
agua aumenta, la diferencia entre áreas va
aumentando. Sin embargo, las secciones:
parabólica, semi-cúbica y semi cúbica con solera
las diferencias de áreas permanecen bajas.
Los valores de caudal para el cual los canales van
a fallar son los siguientes:
So=1.5x10-4 So=2x10-3
Q [m3/s]
Q [m3/s]
Trapezoidal
35
127
Parabólico
36.5
133
Semicúbico
36.1
131
Semicúbico
con solera
36.4
132.5
Semicircular
37.4
137
SECCIÓN
Tabla 11: Valores de caudales, los cuales se van a desbordar el agua que
fluye por las secciones de canal.
Velocidad:
Similar al gráfico de área vs caudal las diferencias
de velocidades son muy parecidas a las diferencias
de áreas, con la diferencia que las secciones con
mayor área representan a las con menores
velocidades. Teniendo la sección con la velocidad
más baja el canal trapezoidal.
45
14
Escuela Superior Politécnica del Litoral
Comparación de tipos de flujos, para diferentes secciones de canales.
Perímetro mojado:
Para pendiente suave, con el caudal inicial, los
perímetros mojados de las secciones semi cúbicas
con y sin ancho de solera y parabólica, son muy
cercano, y a medida que el caudal aumenta, estos
se van separado quedando la sección semi cúbica
con solera entre las secciones mencionadas.
3. Conclusiones
Una vez calculado los valores de tirantes y
velocidades para las diversas secciones posibles,
se eligió como la más factible en términos de
optimización de las propiedades del terreno y que
se adapta mejor a requerimientos técnicos
constructivos, tomando en cuenta las velocidades
recomendadas para que el canal no se vea visto
afectado por sedimentos o posibles socavaciones
o desgaste innecesario de material, es la sección
semi-cúbica, ya que al analizar la misma con una
pendiente ‘suave’, se encuentra en un régimen
sub-crítico, donde si bien es cierto que todas las
secciones presentan similares valores de
velocidad, esta es la sección que menor área
ocupa, con 13,047 m2.
Así mismo en el análisis del canal con una
pendiente ‘fuerte’, el mismo presenta un régimen
super-crítico, que al igual que en caso de la
pendiente ‘suave’, presenta un área de
2,022 m2, inferior en comparación con las otras
áreas de canales calculados; también notándose
una diferencia más notoria en cuanto a las
velocidades de este perfil, en comparación con los
otros.
Por lo tanto, ya sea para una pendiente ‘fuerte’,
como ‘suave’, la sección que mejor se acomoda en
términos de área y velocidades es la semi-cubica,
no obstante, estos no son los únicos parámetros
que tomar en cuenta, ya que en términos
constructivos la sección más óptima puede ser una
figura triangular, rectangular o trapezoidal, a más
de otros factores que pueden influir que otra
sección sea la de preferencia para el ingeniero.
Para caudales altos y con pendientes fuertes, la
sección trapezoidal presenta mayor ralentización
de flujo, esto se debe a que el perímetro es mayor
que el de los demás canales. Por lo que esta tiene
mayor contacto con la superficie y esto favorece a
las fuerzas de fricción, que es una fuerza resistente
al flujo. Por el contrario, para caudales bajos la
sección con mayor perímetro mojado será la semi
cúbica parabólica sin ancho de fondo.
6. Recomendaciones
Tomar en cuenta que las ecuaciones que las
funciones de los canales curvos tienen un factor de
forma, el cual indica el nivel de curvatura que esta
tenga, y este valor toma en cuenta parámetros
como área, altura máxima, entre otros.
Al momento de hacer iteraciones, hacerlas con
variaciones pequeñas, del orden 1 0/00 o 1 0/0, ya
que así se obtienen resultados más confiables
Como se pudo observar en los gráficos de tirante
critico vs caudal, los valores de profundidad de la
sección parabólica y la semi circular son
sumamente cercanos, por lo que, se podría
considerar el cálculo de tirante crítico de la
sección semi circular con la ecuación Ec. 19 como
un método de comprobación para el cálculo del
mismo.
Para ahorrar gastos en excavación y en material,
luego de obtener los tirantes normales, se
recomienda limitar la sección en el sentido que, si
el valor del tirante es mucho menor que la altura
del canal, esta misma altura reducirla hasta
obtener un borde libre recomendable,
manteniendo las mismas características del canal.
En el caso del canal semi circular, dado que en la
ecuación de Manning la incógnita es un, ángulo
tener cuidado que ese ángulo no de más de 180°,
puesto que, si sobrepasa este ángulo, el nivel de
agua se rebosará.
Las familias de canales semi-parabólicos van a
tener una mayor probabilidad de que el agua que
fluye por el canal se encuentre en régimen supercrítico que, en las demás secciones, porque los
tirantes críticos en estas tienden a crecer en
función del caudal mucho más que las demás
secciones.
15
Escuela Superior Politécnica del Litoral
Comparación de tipos de flujos, para diferentes secciones de canales.
7. Trabajos citados
A. M. Campo, & N. B. Aldalur, & S. N.
Fernández, 2012. Morfometría fluvial
aplicada a una cuenca urbana en
Ingeniero White, República Argentina.
Investigaciones Geográficas. ISSN:
0188-4611, DOI: 10.14350/rig.31006
Akan, O. (2008). Open Channel Hydraulics.
Waltham, Massachusetts: ButterworthHeinemann. ISBN: 9780080479804. Pág:
24-25.
Ávila, G. S. (2002). Hidráulica de Canales.
México: Universidad Nacional Autónoma
de México.
Bello. (1914). Coste de las obras hidráulicas en
España. Zaragosa, España: G. Casañal.
ISSN: 0034-8619. Pág: 591-596.
Çengel, Y. A., Cimbala, J. M., & Sknarina, S. F.
(2006).
Mecánica
de
fluidos:
fundamentos y aplicaciones (Vol. 1).
McGraw-Hill. ISBN: 970-10-5612-4.
Pág: 687-691.
Chin-Ping Lin, & Yu-Min Wang, & Samkele S.
Tfwala, & Ching-Nuo Chen 2014. The
Variation of Riverbed Material due to
Tropical Storms in Shi-Wen River,
Taiwan. The Scientific World Journal.
ISSN:
2356-6140,
DOI:
10.1155/2014/580936.
Fox, & McDonald's. (2011). Introduction of Fluid
Mechanics. New York: John Wiley &
Sons, Inc. ISBN: 978-1118355992. Pág:
606-607.
French, R. H. (1993). Hidráulica de Canales
Abiertos. McGraw-Hill. ISBN: 968-451445-X. Pág:163-164.
Goldfarb & da Silva & de Lima & de Azevedo
,2004. Escoamento uniforme em canais
circulares lisos. Parte II: comparação
entre o método de Kazemipour e a
equação de Manning Uniform flow in
smooth circular channels. Part II:
comparison between the Kazemipour
method and the Manning equation.
Revista Brasileira de Engenharia Agrícola
e Ambiental – Agriambi, ISSN: 14154366,
DOI:
10.1590/S141543662004000200003
Han, Y.-C. (2015). Horizontal bottomed semicubic parabolic channel and best
hydraulic section. Journal: CrossMark.
ISSN: 0955-5986. Pag: 56-61
Barroso, D. O., & Suta Ramirez, L. (2007). Flujo
en
Canales
Abiertos.
Pamplona:
Universidad de Pamplona.
J. Aguirre-Pe & M. L. Olivero & A. T. Moncada.
2000, Transporte de sedimentos en
cauces de alta pendiente. IWA the
international wáter association. ISSN:
1134-2196.
DOI:
https://doi.org/10.4995/ia.
Jaromír, Ř & Zbyněk, Z (2015). Flow
characteristics at trapezoidal broadcrested side weir, Journal of Hydrology
and Hydromechanics, ISSN: 0042-790X,
DOI 10.1515/johh-2015-0026
Jhon N. V. Goulart & Carla T. M. Anflor &
Sergio V. Möller, 2013. Static and
dynamic characteristics of turbulent flow
in a closed compound channel. Revista
Facultad de Ingeniería Universidad de
Antioquia, ISSN: 0120-6230
Kay, M. (2008). Practical Hydraulics. New York:
Taylor & Francis. ISBN: 0-203-96077-7.
Pág: 123-127.
Li, Yonghong; Gao, Zhaoliang;. (2014).
Explicit solution for norma ldepth of
parabolic section of open channels.
Yangling: CrossMark. ISSN: 0955-5986.
Pag: 36-39
Mataix, C. (2009). Mecánica de Fluidos y
Maquinarias
Hidráulicas.
Madrid:
Ediciones del Castillo S.A. ISBN: 84219-0175-3. Pág: 7-8.
Méndez, M. V. (2001). Elementos de hidráulica
de canales.
Caracas, Venezuela:
Universidad Católica Andrés Bello.
ISBN: 980-244-252-6. Pág: 79.
Nasseri, A. 2017, Statistical Analysis of
Manning's roughness Coefficients in Nonvegetated Canals for Irrigation and
Drainage Network of Moghan. Majallahi āb va Khāk, ISSN: 2008-4757, DOI
10.22067/jsw.v30i6.41146.
Orson W, I., & Vaughn E, H. (2003). Principios y
aplicaciones del riego (Tercera ed.).
Madrid, España: Reverté. ISBN: 84-2911030-5. Pág: 43.
Pizarro, H. (1994). Introduccion Al Diseno
Hidraulico de Canales Y a la Medicion de
Caudales. Coronado, Costa Rica: IICA
Biblioteca Venezuela. Págs: 12-15.
R. Cadavid, Juan H. (2006). HIDRAULICA DE
CANALES : FUNDAMENTOS. Medellín,
16
Escuela Superior Politécnica del Litoral
Comparación de tipos de flujos, para diferentes secciones de canales.
Colombia: Universidad Eafit. ISBN: 9588281-28-8. Pág: 98-102.
Robert L, M. (2006). Applied Fluid Mechanics.
New York: Pearson Prentice Hall. ISBN:
970-26-0805-8. Pág: 446-447.
Rubio, I. H. (2013). Diseño de Canales. Escuela
Academico Profesional de Ingenieria
Civil.
Ruiz, P. R. (2008). Hidráulica de Canales.
Sotelo, G. (2002). Hidráulica de Canales. México
D.F: UNAM.
Subramanya, K. (2009). Flow in Open Channels.
Naveen Shahdara, Delhi - India: Tata
McGraw-Hill
Publishing Company
Limited. ISBN: 978-0-07-008695-1 Págs:
44-45.
Vatankhah, A. R. (2012). Explicit solutions for
critical and normal depths in trapezoidal
and parabolic open channels. Ain Shams
Engineering Journal. . ISSN: 2090-4479.
Págs: 17-23.
Mironenko AP, W. L. (1984). Parabolic canal
design and analysis. J. Irrig Drain Eng,
Pág: 110. ISSN: 241-6
Achour, B., & Khattaoui, M. (2008). Computation
of Normal and Critical Depths in
Parabolic Cross Sections. The Open Civil
Engineering
Journal,
DOI:
10.2174/1874149500802010009,
Pág:
10.
Han, Y.-C. (2015). Horizontal bottomed semicubic parabolic channel and best
hydraulic section. Jinan, China: ElsevierCollege of Resources and Environment,
University of Jinan, Pág 57-58, ISSN:
0955-5986.
Das, M. M. (2008). Open Channel Flow. Delhi,
India: PHI Learning Pvt. Ltd, Pág 39-40,
ISBN: 8120335228, 9788120335226.
17
View publication stats