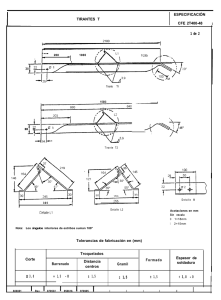
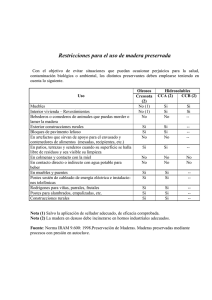
Bloque I: Función real de variable real. Solución Práctica 03_2
Anuncio
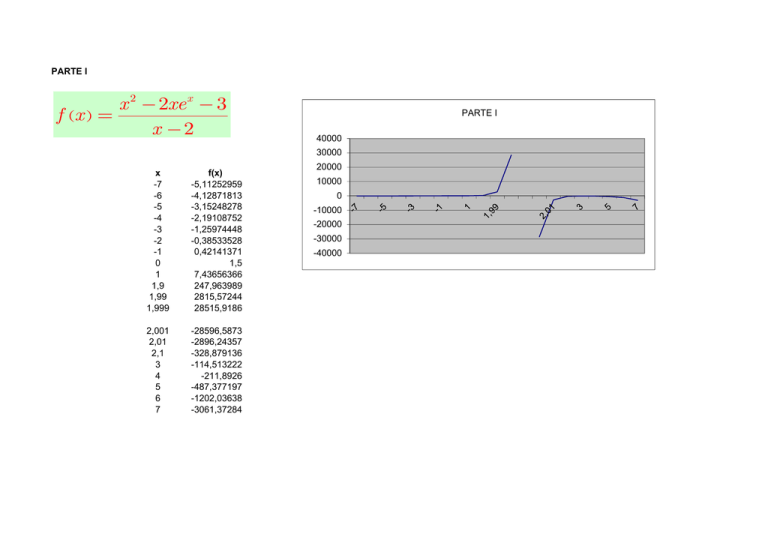
PARTE I x 2 - 2xex - 3 f (x ) = x -2 PARTE I 40000 30000 x -7 -6 -5 -4 -3 -2 -1 0 1 1,9 1,99 1,999 f(x) -5,11252959 -4,12871813 -3,15248278 -2,19108752 -1,25974448 -0,38533528 0,42141371 1,5 7,43656366 247,963989 2815,57244 28515,9186 2,001 2,01 2,1 3 4 5 6 7 -28596,5873 -2896,24357 -328,879136 -114,513222 -211,8926 -487,377197 -1202,03638 -3061,37284 20000 10000 0 -10000 -20000 -30000 -40000 PARTE II Dos postes verticales de 15 y 20 metros están separados por una distancia de 21 metros. El extremo superior de cada una esta unido mediante un tirante a una estaca situada en el suelo entre los postes. ¿En qué lugar deberá colocarse la estaca para que el tirante tenga la longitud total mínima? Solución: 20 15 x 21 - x 2 L (x ) = x 2 + 152 + (21 - x ) + 202 L ¢ (x ) = x x 2 + 152 - 21 - x 2 (21 - x ) + 202 ¢( L x =0 x ) x 2 + 152 = 21 - x 2 (21 - x ) + 202 x (21 - x ) + 202 = (21 - x ) x 2 + 152 x 2 éêë(21 - x ) + 202 ùúû = (21 - x ) (x 2 + 152 ) 2 2 2 202 x 2 = 152 (21 - x ) 20x = 15 (21 - x ) 35x = 15 ⋅ 21 x = 9 L (0) = 152 + 212 + 202 = 15 + 29 = 44 L (9) = 92 + 152 + 122 + 202 = 7 34 » 40, 82 L (21) = 212 + 152 + 202 = 3 74 + 20 » 45, 81 2