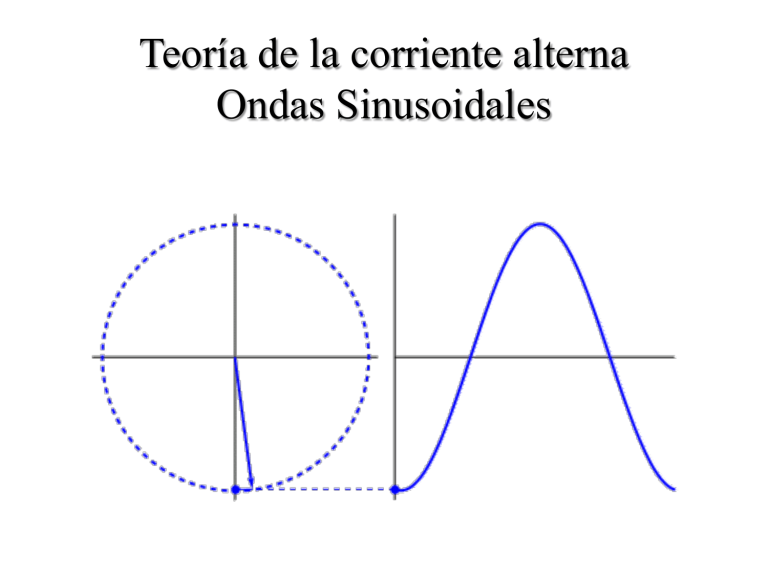
Teoría de la corriente alterna Ondas Sinusoidales Una sinusoide o senoide es una señal que tiene la forma de la función seno o coseno. La forma de onda sinusoidal u onda seno es el tipo fundamental de corriente alterna (ca) y voltaje alterno. También se conoce como onda sinusoidal o, simplemente, sinusoide. Dos tipos de fuentes producen voltajes sinusoidales: las máquinas eléctricas rotatorias (generadores de ca) y los circuitos osciladores electrónicos, los cuales se utilizan en instrumentos comúnmente conocidos como generadores de señales electrónicas. El servicio eléctrico provisto por la compañía de electricidad es en la forma de voltaje y corriente sinusoidales. La corriente senoidal se invierte a intervalos regulares y tiene valores alternadamente positivo y negativo. Los circuitos excitados por fuentes de corriente o tensión senoidal se llaman circuitos de ca. Dos tipos de fuentes producen voltajes sinusoidales: las máquinas eléctricas rotatorias (generadores de ca) y los circuitos osciladores electrónicos, los cuales se utilizan en instrumentos comúnmente conocidos como generadores de señales electrónicas. La gráfica muestra la forma general de una onda seno, la cual puede ser o una corriente alterna o un voltaje alterno. El voltaje (o la corriente) se muestra en el eje vertical y el tiempo (t) en el eje horizontal. Se observa cómo varía el voltaje (o la corriente) con el tiempo. Comenzando en cero, el voltaje (o la corriente) se incrementa hasta un máximo positivo (pico), regresa a cero, y luego se incrementa hasta un máximo negativo (pico) antes de regresar otra vez a cero, y así completa un ciclo. Periodo de una onda seno Una onda seno varía con el tiempo (t) de una manera que es definible. El tiempo requerido para que una onda seno complete todo un ciclo se llama periodo (T) Frecuencia de una onda seno La frecuencia (f) es el número de ciclos que una onda seno completa en un segundo. Mientras más ciclos se completan en un segundo, más alta es la frecuencia. La frecuencia (f) se mide en unidades de Hertz (Hz) . Un Hz equivale a un ciclo por segundo; 60 Hz son 60 ciclos por Segundo. Baja Frecuencia Alta Frecuencia Amplitud de onda La distancia entre un valor máximo de la función y el eje x es la amplitud de la onda senoidal. Mientras que la longitud de onda es la distancia existente entre dos valores máximos consecutivos en la gráfica de la función. Así, amplitud y longitud de onda son siempre valores positivos. La unidad de medición para el eje horizontal es el grado. Una segunda unidad de medición utilizada con frecuencia es el radián (rad). Este se define mediante un cuadrante de un circulo, donde la distancia sobre la circunferencia es igual al radio del circulo. Onda senoidal con el eje horizontal en grados. Definición de radian Si definimos a x como el número de intervalos de r (el radio) alrededor de la circunferencia del círculo, entonces: 𝑪 = 𝟐𝝅𝒓 = 𝒙 ∙ 𝒓 = 𝟐𝝅 𝒓𝒂𝒅 = 𝟑𝟔𝟎° Por tanto, existen 2π radianes alrededor de un círculo de 360º Con lo mencionado anteriormente, tenemos que: 𝟏 𝒓𝒂𝒅 = 𝟓𝟕. 𝟐𝟗𝟔° = 𝟓𝟕, 𝟑° Muchas fórmulas eléctricas contienen un múltiplo de π. Por tal motivo, es preferible medir los ángulos en radianes en lugar de hacerlo en grados. Grados a radianes y radianes a grados. 𝝅 𝑹𝒂𝒅𝒊𝒂𝒏𝒆𝒔 = × 𝒈𝒓𝒂𝒅𝒐𝒔 𝟏𝟖𝟎° 𝟏𝟖𝟎° 𝑮𝒓𝒂𝒅𝒐𝒔 = × (𝒓𝒂𝒅𝒊𝒂𝒏𝒆𝒔) 𝝅 Ejercicios: Convierta de radianes a grados o viceversa, según sea el caso. 1. 90°= rad 2. 30°= rad 3. π 𝑟𝑎𝑑 3 4. 3π 𝑟𝑎𝑑 2 = = ° ° FORMATO GENERAL PARA EL VOLTAJE Y LA CORRIENTE SENOIDALES El formato matemático general básico de la forma de onda senoidal es 𝑨𝒎 𝐬𝐢𝐧 𝝎𝒕 donde Am - la amplitud de la senoide 𝝎 - la frecuencia angular en radianes/s t - es el tiempo en segundos 𝜽 = 𝝎t - el argumento de la senoide o el ángulo a través del cual pasara el vector rotatorio. Para cantidades eléctricas, como corriente y voltaje, el formato general es 𝒊 = 𝑰𝒎 sin 𝝎𝒕 = 𝑰𝒎 𝐬𝐢𝐧 𝜽 𝒆 = 𝑬𝒎 sin 𝝎𝒕 = 𝑬𝒎 𝐬𝐢𝐧 𝜽 Donde las letras mayúsculas con el subíndice m representan la amplitud, y las letras minúsculas i y e representan el valor instantáneo de la corriente y el voltaje, respectivamente, en cualquier instante t. Para la siguiente forma de onda senoidal determine: a. b. c. d. e. ¿Cuál es el valor pico? ¿Cuál es el valor instantáneo a 15 ms y 20 ms? ¿Cuál es el valor pico a pico de la forma de onda? ¿Cuál es el periodo de la forma de onda? ¿Cuántos ciclos se muestran? Para la siguiente forma de onda senoidal determine: a. ¿Cuál es el valor pico? b. ¿Cuál es el valor instantáneo a 1 µs y 7 µs? c. ¿Cuál es el valor pico a pico de la forma de onda? d. ¿Cuál es el periodo de la forma de onda? e. ¿Cuántos ciclos se muestran? 𝒗 𝒕 = 𝑽𝟎 𝐜𝐨𝐬 𝝎𝒕 ± 𝜽 𝑽𝟎 = 𝐴𝑚𝑝𝑙𝑖𝑡𝑢𝑑 𝝎 = 𝑣𝑒𝑙𝑜𝑐𝑖𝑑𝑎𝑑 𝑜 𝑓𝑟𝑒𝑐𝑢𝑒𝑛𝑐𝑖𝑎 𝑎𝑛𝑔𝑢𝑙𝑎𝑟 𝑒𝑛 𝑟𝑎𝑑𝑖𝑎𝑛𝑒𝑠 𝝎𝒕 = 𝑎𝑟𝑔𝑢𝑚𝑒𝑛𝑡𝑜 𝑑𝑒 𝑙𝑎 𝑠𝑒𝑛𝑜𝑖𝑑𝑒 𝜽 = 𝑎𝑛𝑔𝑢𝑙𝑜 𝑑𝑒 𝑓𝑎𝑠𝑒 𝝎= 𝟐𝝅 𝑻 = 𝟐𝝅𝒇 𝟏 𝒇 𝑻= = 𝟐𝝅 𝝎 𝒇= 𝟏 𝑻 = 𝝎 𝟐𝝅 Si una forma de onda senoidal recorre un ángulo de 30° en 5 seg, determine ω. Determine la Amplitud y frecuencia de las siguientes ondas: a) 20 𝑠𝑖𝑛 377𝑡 b) 12 𝑠𝑖𝑛 2𝜋120𝑡 c) 106 𝑠𝑖𝑛 10000𝑡 d) −8 𝑠𝑖𝑛 10.058𝑡 Determine la ω a) 1.8s e) 100Hz b) 0.3ms f) 0.25kHz c) 8µs g) 2kHz d) 4µs h) 0.004Hz Determine la frecuencia y el periodo cuando ω es: a) 750 rad/s b) 12 rad/s c) 600 rad/s Ejercicio: Trace 𝟔 𝐬𝐢𝐧 𝟕𝟓𝟒𝒕 con la abscisa a) Angulo en grados. b) Angulo en radianes. c) Tiempo en segundos. Considerando 𝒗 𝒕 = 𝑽𝟎 𝐜𝐨𝐬 𝝎𝒕 + 𝜽 𝑦 𝒗 𝒕 = 𝑽𝒎 𝐬𝐢𝐧 𝝎𝒕 Ejemplo: Dibuje 𝒗 𝒕 = 𝟓 𝒄𝒐𝒔 𝝅𝒕Τ 𝟔 + 𝟑𝟎° La ecuación se puede reescribir de la siguiente manera: 𝒗 𝒕 = 𝟓 𝒄𝒐𝒔 𝝅𝒕ൗ𝟔 + 𝝅ൗ𝟔 = 𝟓 𝐜𝐨𝐬 𝝅 𝒕 + 𝟏 ൗ𝟔 Ejemplos: Dibuje las siguientes ondas senoidales: a) 𝒗 𝒕 = 𝟐 𝒄𝒐𝒔 𝝅𝒕Τ 𝟒 − 𝟒𝟓° RELACIONES DE FASE. Si la forma de onda se desplaza a la derecha o a la izquierda de 0°, la expresión deriva en: 𝑨𝒎 𝐬𝐢𝐧 𝝎𝒕 ± 𝜽 donde θ es el ángulo en grados o radianes que la forma de onda ha sido desplazada. Si la forma de onda pasa a través del eje horizontal con una pendiente de tendencia positiva (incrementándose con el tiempo) antes de 0°, como se muestra en la figura, la expresión es: 𝑨𝒎 𝐬𝐢𝐧 𝝎𝒕 + 𝜽 Con ωt = α = 0°, la magnitud esta determinada por 𝑨𝒎 𝐬𝐢𝐧 𝜽. Si la forma de onda pasa a través del eje horizontal con una pendiente de tendencia positiva después de 0°, como se muestra en la figura, la expresión es: 𝑨𝒎 𝐬𝐢𝐧 𝝎𝒕 − 𝜽 Y en ωt = α = 0°, la magnitud es 𝑨𝒎 𝐬𝐢𝐧 −𝜽 , lo cual, mediante una identidad trigonométrica, es −𝑨𝒎 𝐬𝐢𝐧 𝜽. Si la forma de onda cruza el eje horizontal con una pendiente de tendencia positiva de 90° (π/2) antes, como se muestra en la figura, se denomina onda cosenoidal; es decir, 𝝅 𝐬𝐢𝐧 𝝎𝒕 + 𝟗𝟎° = 𝐬𝐢𝐧 𝝎𝒕 + = 𝐜𝐨𝐬 𝝎𝒕 𝟐 O bien 𝐬𝐢𝐧 𝝎𝒕 = 𝐜𝐨𝐬 𝝎𝒕 − 𝟗𝟎° = 𝐜𝐨𝐬 𝝎𝒕 − 𝝅 𝟐 Los términos adelantar y retrasar se utilizan para indicar la relación entre dos formas de onda senoidales de la misma frecuencia graficadas sobre el mismo conjunto de ejes. En la curva del coseno se dice que adelanta a la curva del seno por 90°, y la curva del seno se dice que se retrasa con respecto a la curva del coseno por 90°. Los 90° son referidos como el ángulo de fase entre las dos formas de onda. Además, se debe tener presente que: sin −𝛼 = − sin 𝛼 cos −𝛼 = cos 𝛼 Si una expresión senoidal se presenta como: 𝑒 = −𝐸𝑚 sin 𝜔𝑡 el signo negativo estará asociado con la parte senoidal de la expresión, no con el valor pico 𝐸𝑚 . En otras palabras, la expresión, por conveniencia, deberá escribirse como: 𝑒 = 𝐸𝑚 (−sin 𝜔𝑡) Corriente instantánea en elementos eléctricos, resistivos, inductivos y capacitivos. Resistor o resistencia. Para frecuencias de líneas de alimentación y frecuencias de hasta unos cientos de kilohertz, la resistencia, para todo propósito practico, no es afectada por la frecuencia del voltaje o la corriente senoidales aplicados. Para esta región de frecuencia, el resistor R de la figura puede manejarse como una constante, y se podrá aplicar la ley de Ohm de la siguiente forma. 𝑣 = 𝑉𝑚 sin 𝜔𝑡 𝒗 𝑽𝒎 𝐬𝐢𝐧 𝝎𝒕 𝑽𝒎 𝒊= = = 𝐬𝐢𝐧 𝝎𝒕 = 𝑰𝒎 𝐬𝐢𝐧 𝝎𝒕 𝑹 𝑹 𝑹 Por lo mencionado en la diapositiva anterior, tenemos: 𝑽𝒎 𝑰𝒎 = → 𝑽𝒎 = 𝑰𝒎 𝑹 𝑹 para un elemento puramente resistivo, el voltaje y la corriente a través del elemento se encuentran en fase, con sus valores pico relacionados mediante la ley de Ohm. Ejemplos: 1. Se indica el voltaje en un resistor. Encuentre la expresión senoidal para la corriente si el resistor es de 10Ω. Trace las curvas para v e i. a) v =100 sen 377t b) v =25 sen (377t+60) 2. Se proporciona la corriente a través de un resistor de 5Ω. Encuentre la expresión senoidal para el voltaje en el resistor para i = 40 sen (377t + 30°). Inductor e Inductancia. El voltaje en un inductor se relaciona directamente con la razón de cambio de la corriente a través de la bobina. Por consiguiente, a mayor frecuencia, mayor será la razón de cambio de la corriente a través de la bobina, y mas grande la magnitud del voltaje. Además, que la inductancia de una bobina determinara la razón de cambio del flujo de enlace de una bobina para un cambio particular en la corriente a través de la misma. Mientras mas alta sea la inductancia, mayor será la razón de cambio de los enlaces del flujo y mayor el voltaje resultante en la bobina. Por lo que, el voltaje inductivo estará directamente relacionado con la frecuencia (o, con mayor precisión, con la velocidad angular de la corriente senoidal de ca a través de la bobina) y con la inductancia de la bobina. Para valores crecientes de f en la figura, la magnitud de 𝑣𝐿 se incrementará por lo mencionado anteriormente. Dado que 𝑣𝐿 se incrementará tanto con 𝜔 = 2𝜋𝑓 y L, como con L, la oposición de un elemento inductivo es como se define en la figura. Para el inductor 𝒅𝒊𝑳 𝒗𝑳 = 𝑳 𝒅𝒕 y, al aplicar diferenciación, 𝒅𝒊𝑳 𝒅 = 𝑰𝒎 𝐬𝐢𝐧 𝝎𝒕 = 𝝎𝑰𝒎 𝐜𝐨𝐬 𝝎𝒕 𝒅𝒕 𝒅𝒕 Por lo tanto, 𝒗𝑳 = O bien: Donde: 𝒅𝒊𝑳 𝑳 𝒅𝒕 = 𝑳 𝝎𝑰𝒎 𝒄𝒐𝒔𝝎𝒕 = 𝝎𝑳𝑰𝒎 𝒄𝒐𝒔𝝎𝒕 𝒗𝑳 = 𝑽𝒎 𝐬𝐢𝐧 𝝎𝒕 + 𝟗𝟎° 𝑽𝒎 = 𝝎𝑳𝑰𝒎 La grafica de v e i en la figura muestra que: L L para un inductor, vL adelanta a iL por 90°, o está retrasada con respecto a vL por 90°. Si un ángulo de fase esta incluido en la expresión senoidal de iL, tal que como: 𝒊𝑳 = 𝑰𝒎 𝐬𝐢𝐧 𝝎𝒕 ± 𝜽 Entonces 𝒗𝑳 = 𝝎𝑳𝑰𝒎 𝐬𝐢𝐧 𝝎𝒕 ± 𝜽 + 𝟗𝟎 La oposición establecida por un inductor en una red de ca senoidal podrá encontrarse ahora aplicando la ecuación: 𝒄𝒂𝒖𝒔𝒂 𝒄𝒂𝒖𝒔𝒂 𝑬𝒇𝒆𝒄𝒕𝒐 = → 𝑶𝒑𝒐𝒔𝒊𝒄𝒊ó𝒏 = 𝒐𝒑𝒐𝒔𝒊𝒄𝒊ó𝒏 𝒆𝒇𝒆𝒄𝒕𝒐 Sustituyendo variables se tiene 𝑽𝒎 𝝎𝑳𝑰𝒎 𝑶𝒑𝒐𝒔𝒊𝒄𝒊ó𝒏 = = = 𝝎𝑳 𝑰𝒎 𝑰𝒎 Por lo cual, se puede concluir que la oposición establecida por un inductor en la red senoidal de ca se relaciona directamente con el producto de la velocidad angular (𝝎 = 𝟐𝝎𝒇) y la inductancia. Al producto 𝝎𝑳 se le denomina reactancia (reacción) de un inductor, la cual se simboliza 𝑋𝐿 y sus unidades son los ohms. Y en su forma de ley de Ohm, se puede determinar con 𝑽𝒎 𝑿𝑳 = (𝐨𝐡𝐦𝐬, 𝜴) 𝑰𝒎 Ejemplos: 1. Se proporciona la corriente que fluye a través de una bobina de 0.1H. Determine la expresión senoidal para el voltaje de la bobina. Trace las curvas v e i. a) i =10 sen 377t b) i =7 sen (377t-70°) 2. Se proporciona el voltaje que pasa a través de una bobina de 0.5 H ¿Cuál es la expresión senoidal para la corriente? 𝑣 = 100 sin 20𝑡 Capacitor o Capacitancia. En redes capacitivas, el voltaje en el capacitor está limitado por la razón a la que puede depositarse la carga en, o liberarse por, las placas del capacitor durante las fases de carga y descarga, respectivamente. Es decir, un cambio instantáneo en el voltaje en un capacitor es opuesto por el hecho de que existe un elemento de tiempo requerido para depositar carga sobre (o liberar carga desde) las placas de un capacitor, y 𝑽 = 𝑸/𝑪. Dado que la capacitancia es una medida de la razón a la que el capacitor almacena carga sobre sus placas, “para un cambio particular en el voltaje en el capacitor, a mayor valor de capacitancia, mayor será la corriente capacitiva resultante”. “para una capacitancia en particular, mientras mayor sea la razón de cambio de voltaje en el capacitor, mayor será la corriente capacitiva”. La corriente de un capacitor, por tanto, esta relacionada directamente con la frecuencia o, específicamente, con la velocidad angular y con la capacitancia del capacitor. Un incremento en cualquier cantidad dará por resultado un incremento en la corriente del capacitor. Como un incremento en la corriente corresponde a una disminución en la oposición, e 𝒊𝑪 es proporcional a ω y C, la oposición de un capacitor estará inversamente relacionada con 𝝎 = 𝟐𝝅𝒇 y C. Para el capacitor de la figura se tiene que: 𝑑𝑣𝐶 𝑖𝐶 = 𝐶 𝑑𝑡 Y aplicando diferenciación, se tiene que 𝑑𝑣𝐶 𝑑 = 𝑉𝑚 sin 𝜔𝑡 = 𝜔𝑉𝑚 𝑐𝑜𝑠𝜔𝑡 𝑑𝑡 𝑑𝑡 Por lo tanto 𝑑𝑣𝐶 𝑖𝐶 = 𝐶 = 𝐶 𝜔𝑉𝑚 cos 𝜔𝑡 = 𝜔𝐶𝑉𝑚 cos 𝜔𝑡 𝑑𝑡 o 𝑖𝐶 = 𝐼𝑚 sin 𝜔𝑡 + 90° Donde 𝐼𝑚 = 𝜔𝐶𝑉𝑚 La grafica de v e i en la figura muestra que: C C en un capacitor iC va 90° delante de vC, o vC va 90° detrás de iC. Si el ángulo de fase esta incluido en la expresión senoidal para vC, tal como: 𝑣𝐶 = 𝑉𝑚 sin 𝜔𝑡 ± 𝜃 entonces 𝑖𝐶 = 𝜔𝐶𝑉𝑚 sin 𝜔𝑡 ± 𝜃 + 90° Aplicando 𝒄𝒂𝒖𝒔𝒂 𝑽𝒎 𝑽𝒎 𝟏 𝑶𝒑𝒐𝒔𝒊𝒄𝒊ó𝒏 = = = = 𝒆𝒇𝒆𝒄𝒕𝒐 𝑰𝒎 𝝎𝑪𝑽𝒎 𝝎𝑪 A 𝟏Τ𝝎𝑳 se le denomina reactancia de un capacitor, la cual se simboliza 𝑿𝑪 y se mide en ohms. Y en su forma de ley de Ohm, se puede determinar con 𝟏 𝑽𝒎 𝑿𝑪 = = (𝐨𝐡𝐦𝐬, 𝜴) 𝝎𝑪 𝑰𝒎 Ejemplos. 1. A continuación, se proporciona el voltaje en un capacitor de 1µF. ¿Cual es la expresión senoidal para la corriente? Trace las curvas de i y v. 𝑣 = 30 sin 400𝑡 2. Se proporciona la corriente a través de un capacitor de 100 µF. Encuentre la expresión senoidal para el voltaje en el capacitor. 𝑖 = 40 sin 500𝑡 + 60°